- 1 -
WZORY – STATYSTYKA MATEMATYCZNA
1. RACHUNEK PRAWDOPODOBIEŃSTWA
Prawdopodobieństwo zajścia zdarzenia A:
2. ZMIENNE LOSOWE
Funkcja rozkładu prawdopodobieństwa zmiennej losowej dyskretnej X:
,
Dystrybuanta zmiennej losowej dyskretnej X:
Funkcja gęstości prawdopodobieństwa zmiennej losowej ciągłej X:
,
Dystrybuanta dla zmiennej losowej ciągłej X:
3. PARAMETRY ZMIENNYCH LOSOWYCH:
Wartość oczekiwana skokowej zmiennej losowej X:
Wartość oczekiwana ciągłej zmiennej losowej X:
Wariancja skokowej zmiennej losowej X:
Odchylenie standardowe zmiennej losowej X:
Odchylenie standardowe zmiennej losowej X:
4. WYBRANE ROZKŁADY DYSKRETNE
Rozkład dwumianowy (Bernoulliego):
, ,
A
A
P
)
(
i
i
p
x
X
P
)
(
1
1
k
i
i
p
x
x
i
i
p
x
X
P
x
F
)
(
)
(
0
)
(
x
f
1
)
(
dx
x
f
x
dt
t
f
x
X
P
x
F
)
(
)
(
)
(
k
i
i
i
p
x
X
E
1
)
(
dx
x
xf
X
E
)
(
)
(
)
(
)
(
)
(
2
1
2
1
1
2
2
X
E
p
x
p
X
E
x
X
D
k
i
i
k
i
i
i
)
(
)
(
)
(
)
(
)
(
2
2
2
2
X
E
dx
x
f
x
dx
x
f
X
E
x
X
D
i
)
(
)
(
2
X
D
X
D
k
n
k
p
p
k
n
k
X
P
1
)
(
np
X
E
)
(
p
np
X
D
1
)
(
2
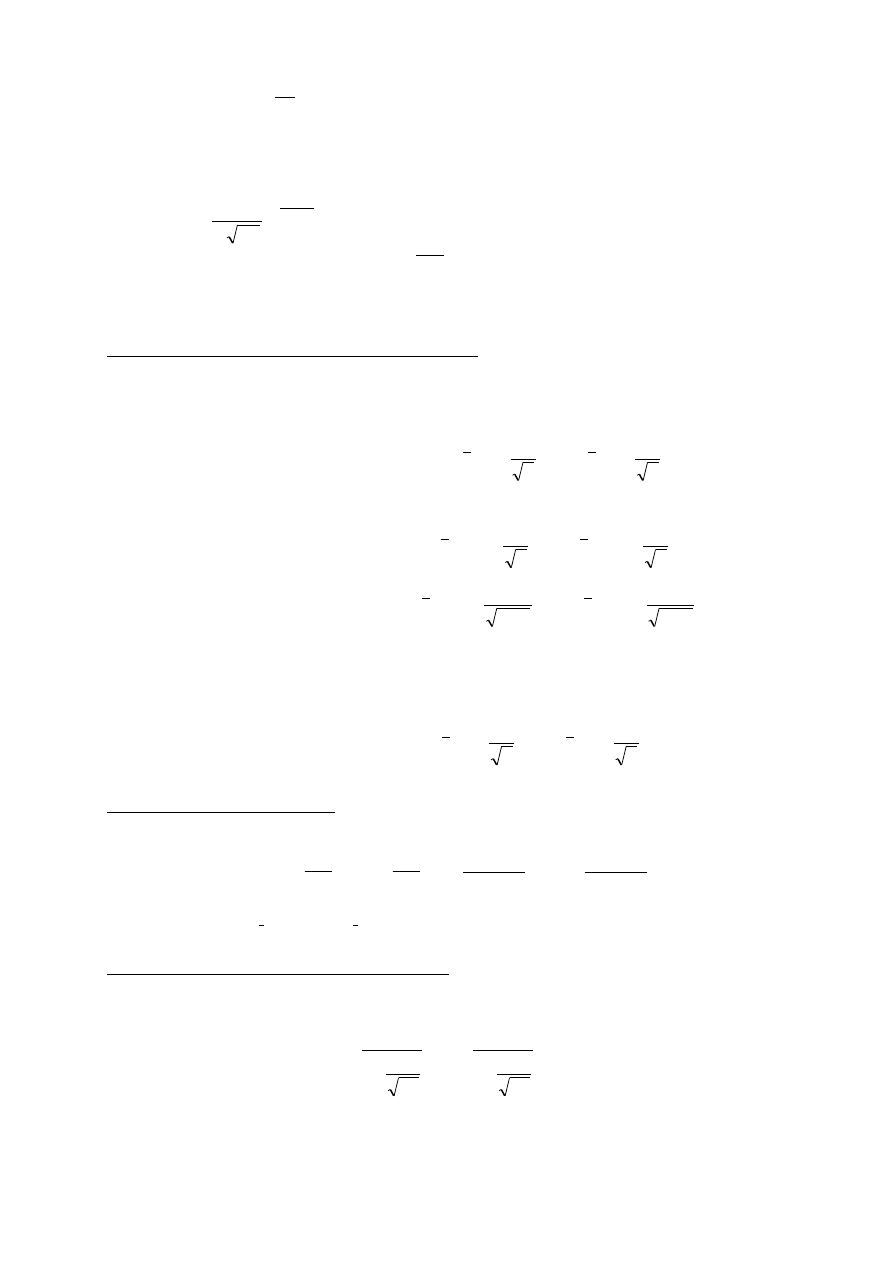
- 2 -
Rozkład Poissona:
, ,
5. WYBRANE ROZKŁADY CIĄGŁE
Rozkład normalny :
Standaryzacja:
6. PRZEDZIAŁY UFNOŚCI
Przedział ufności dla średniej (wartości oczekiwanej)
:
MODEL I
Populacja ma rozkład normalny N(
;
);
- znane:
MODEL II
Populacja ma rozkład normalny N(
;
);
- nieznane; n≤30:
lub
MODEL III
Populacja ma rozkład normalny N(
;
) lub dowolny inny rozkład zbliżony do rozkładu
normalnego;
- nieznane; n>30:
Przedział ufności dla wariancji
2
:
Populacja ma rozkład normalny N(
;
); n≤30:
lub
gdzie
2
1
;
1
1
2
1
n
c
,
2
1
;
2
2
1
n
c
Przedział ufności dla odchylenie standardowego
:
Populacja ma rozkład normalny N(
;
) lub zbliżony do normalnego; n>30:
e
k
k
X
P
k
!
)
(
)
( X
E
)
(
2
X
D
;
N
2
2
2
2
1
)
(
x
e
x
f
1
;
0
~
;
~
N
U
N
X
X
U
n
u
x
n
u
x
n
s
t
x
n
s
t
x
n
n
ˆ
ˆ
1
,
1
,
1
1
1
,
1
,
n
s
t
x
n
s
t
x
n
n
n
s
u
x
n
s
u
x
1
2
2
2
2
c
ns
c
ns
1
2
2
2
2
ˆ
1
ˆ
1
c
s
n
c
s
n
n
u
s
n
u
s
2
1
2
1
- 3 -
Przedział ufności dla wskaźnika struktury p:
7. MINIMALNA LICZEBNOŚĆ PRÓBY
MODEL I
Populacja ma rozkład normalny N(
;
);
- znane:
MODEL II
Populacja ma rozkład normalny N(
;
);
- nieznane:
gdzie jest wariancją wyznaczoną z próby wstępnej o liczebności n
0
zgodnie z wzorem:
MODEL III
Populacja ma rozkład dwupunktowy:
jeżeli znany jest spodziewany rząd wielkości szacowanego
wskaźnika struktury (p);
jeżeli nie jest znany rząd wielkości szacowanego wskaźnika
struktury (p).
8. PARAMETRYCZNE TESTY ISTOTNOŚCI
Test istotności dla średniej (wartości oczekiwanej)
:
lub lub
MODEL I
Jeżeli populacja ma rozkład normalny N(
;
);
- znane, to sprawdzianem hipotezy zerowej jest
statystyka:
o rozkładzie normalnym N(0;1).
MODEL II
Jeżeli populacja ma rozkład normalny N(
;
);
- nieznane, n≤30, to sprawdzianem hipotezy
zerowej jest statystyka:
o rozkładzie t-Studenta o (n-1) stopniach swobody.
MODEL III
Jeżeli populacja ma rozkład normalny N(
;
) lub zbliżony do rozkładu normalnego;
- nieznane,
n>30, to sprawdzianem hipotezy zerowej jest statystyka:
o rozkładzie normalnym N(0;1).
n
n
m
n
m
u
n
m
p
n
n
m
n
m
u
n
m
1
1
2
2
2
d
u
n
2
2
2
1
,
ˆ
0
d
s
t
n
n
2
ˆs
0
1
2
0
2
1
1
ˆ
n
i
i
x
x
n
s
2
2
1
d
p
p
u
n
2
2
4d
u
n
0
0
:
H
0
1
:
H
0
1
:
H
0
1
:
H
n
x
u
0
1
ˆ
0
0
n
s
x
n
s
x
t
n
s
x
u
0
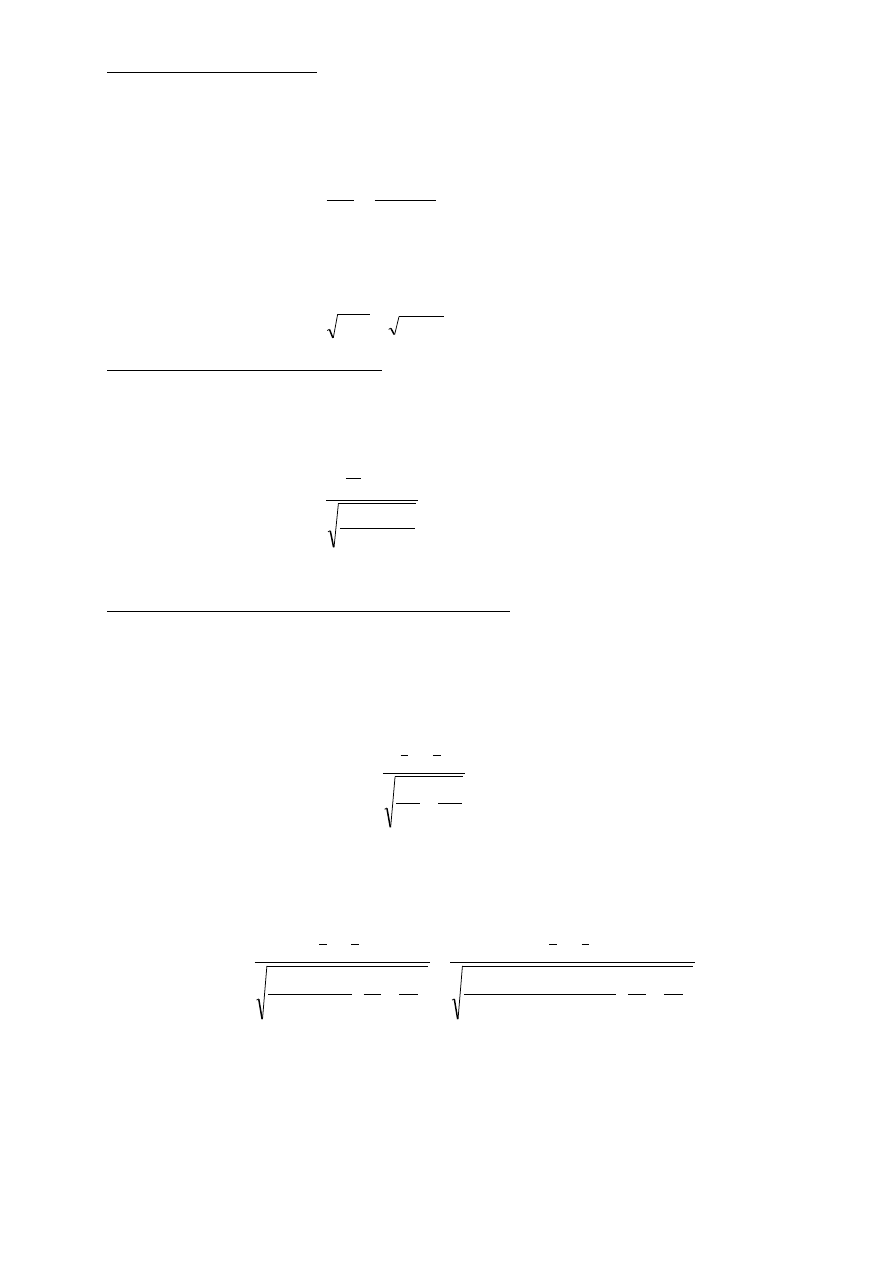
- 4 -
Test istotności dla wariancji
2
:
Jeżeli populacja ma rozkład normalny N(
;
) to sprawdzianem hipotezy zerowej jest statystyka:
o rozkładzie z (n-1) stopniami swobody.
Jeżeli liczebność próby n>30, wówczas rozkład należy przybliżyć rozkładem normalnym N(0;1)
zgodnie z następującym przekształceniem:
Test istotności dla wskaźnika struktury p:
lub lub
Jeżeli populacja ma dwupunktowy, to sprawdzianem hipotezy zerowej jest statystyka:
o rozkładzie normalnym N(0;1).
Test istotności dla dwóch średnich (wartości oczekiwanych):
lub lub
MODEL I
Jeżeli populacje mają rozkłady normalne N(
1
;
1
) i N(
2
;
2
) lub zbliżone do rozkładów
normalnych;
1,
2
nieznane, to sprawdzianem hipotezy zerowej jest statystyka:
o rozkładzie normalnym N(0;1).
MODEL II
Jeżeli populacje mają rozkłady normalne N(
1
;
1
) i N(
2
;
2
);
1,
2
nieznane,
1
=
2
, n
1
≤30,
n
2
≤30, to sprawdzianem hipotezy zerowej jest statystyka:
o rozkładzie t-Studenta o (n
1
+n
2
1) stopniach swobody.
2
0
2
0
:
H
2
0
2
1
:
H
2
0
2
2
0
2
2
ˆ
1
s
n
ns
2
2
3
2
2
2
n
u
0
0
:
p
p
H
0
1
:
p
p
H
0
1
:
p
p
H
0
1
:
p
p
H
2
1
0
:
H
2
1
1
:
H
2
1
1
:
H
2
1
1
:
H
n
p
p
n
m
u
0
0
0
1
2
2
2
1
2
1
2
1
n
n
x
x
u
2
1
2
1
2
2
2
2
1
1
2
1
2
1
2
1
2
2
2
2
1
1
2
1
1
1
2
ˆ
1
ˆ
1
1
1
2
n
n
n
n
s
n
s
n
x
x
n
n
n
n
s
n
s
n
x
x
t
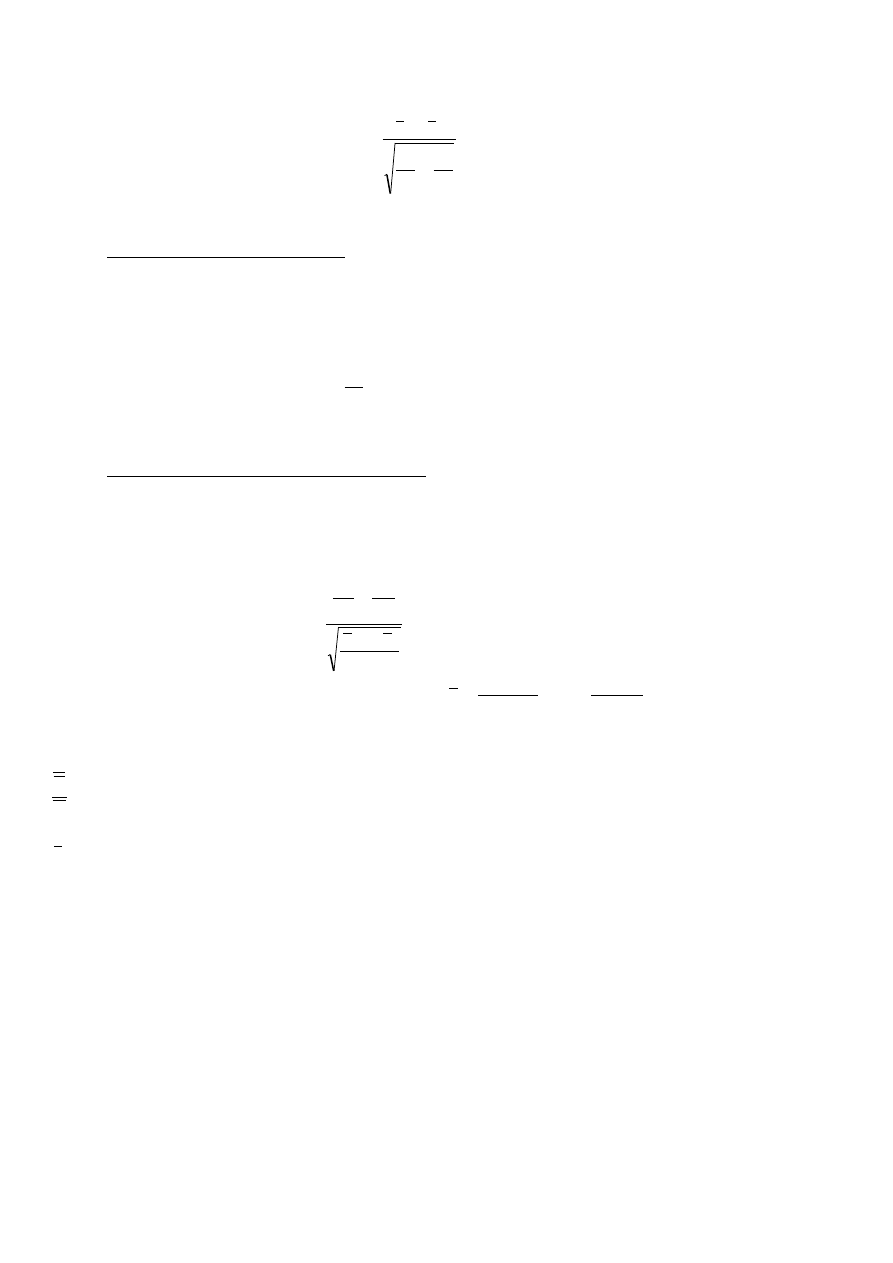
- 5 -
MODEL III
Jeżeli populacje mają rozkłady normalne N(
1
;
1
) i N(
2
;
2
);
1,
2
znane,
n
1
>30, n
2
>30 to sprawdzianem hipotezy zerowej jest statystyka:
o rozkładzie normalnym N(0;1).
Test istotności dla dwóch wariancji:
Jeżeli populacja ma rozkład normalny N(
;
) lub zbliżony do rozkładu normalnego, to
sprawdzianem hipotezy zerowej jest statystyka:
,
o rozkładzie F-Snedecora z i stopniami swobody.
Test istotności dla dwóch wskaźników struktury:
lub lub
Jeżeli populacja ma dwupunktowy, to sprawdzianem hipotezy zerowej jest statystyka:
o rozkładzie normalnym N(0;1), gdzie: , .
OZNACZENIA:
liczba zdarzeń elementarnych sprzyjających zajściu zdarzenia A;
liczba wszystkich zdarzeń elementarnych;
n
liczebność próby;
średnia z próby;
s
odchylenie standardowe z próby (estymator obciążony);
odchylenie standardowe z próby (estymator nieobciążony);
średnia populacji;
odchylenie standardowe populacji;
p
wskaźnik struktury populacji;
m
liczba elementów wyróżnionych z n
elementowej próby;
d
dopuszczalny, ustalony z góry maksymalny błąd szacunku średniej lub wskaźnika struktury.
A
2
2
2
1
0
:
H
2
2
2
1
1
:
H
2
1
0
:
p
p
H
2
1
1
:
p
p
H
2
1
1
:
p
p
H
2
1
1
:
p
p
H
n
p
p
n
m
n
m
u
1
2
2
1
1
2
1
2
1
n
n
m
m
p
2
1
2
1
n
n
n
n
n
2
2
2
1
ˆ
ˆ
s
s
F
1
1
n
1
2
n
2
2
2
1
ˆ
ˆ
s
s
2
2
2
1
2
1
2
1
n
s
n
s
x
x
u
x
sˆ