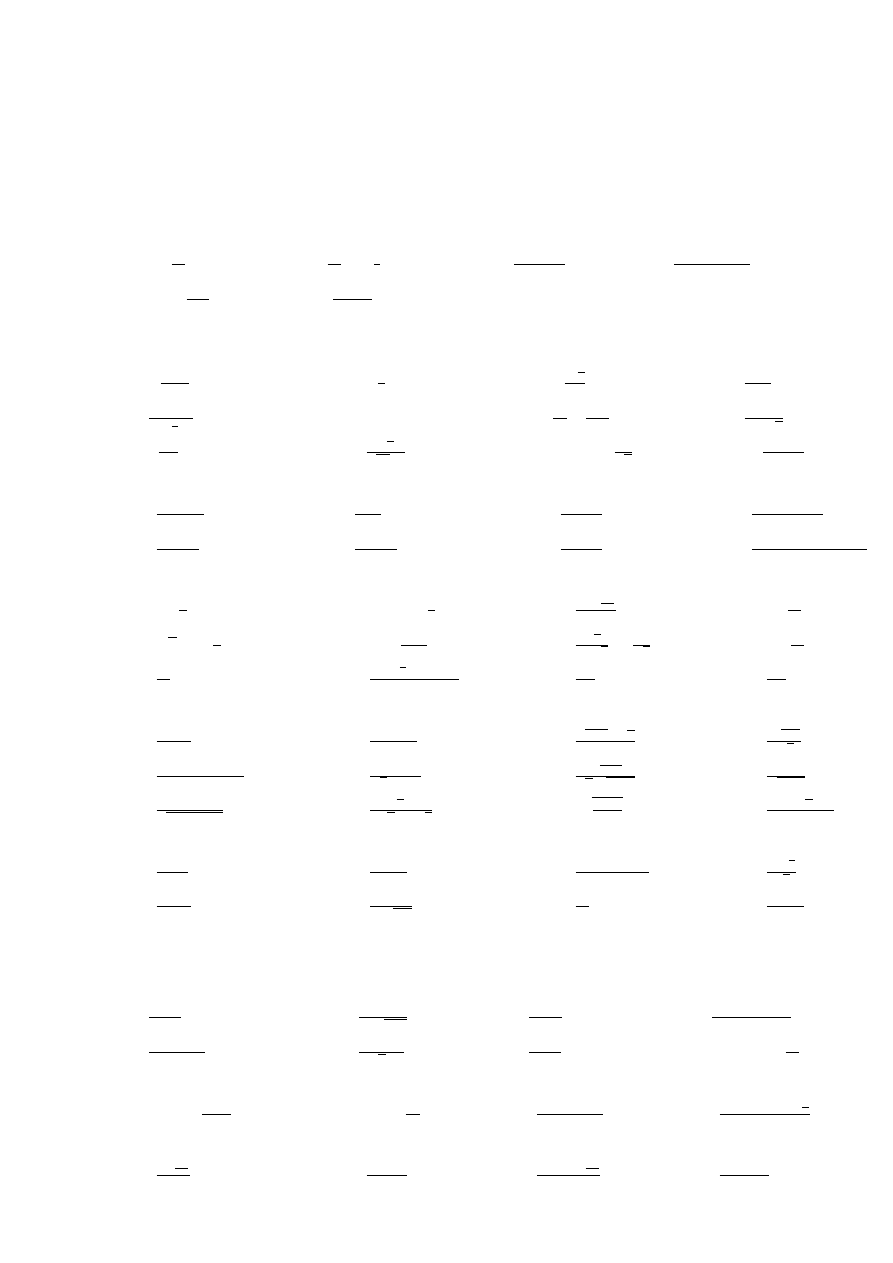
Wydział WILiŚ, Budownictwo, sem.3

dr Jolanta Dymkowska

Szeregi liczbowe

Zad.1 Zbadaj z definicji zbieżność szeregów:

1.1

∞

P

n=1

3

5

n

1.2

∞

P

n=1

1

4

n

+

6
7

n

1.3

∞

P

n=1

1

n

2

+3n+2

1.4

∞

P

n=1

1

(3n−2)(3n+1)

1.5

∞

P

n=1

ln

n+2
n+1

1.6

∞

P

n=1

ln

n(n+2)

(n+1)

2

Zad.2 Zbadaj zbieżność szeregów o wyrazach nieujemnych:

2.1

∞

P

n=1

3n−1
4n+5

n

2.2

∞

P

n=1

sin

1

n

n

2.3

∞

P

n=1

n

√

n

7

n

2.4

∞

P

n=1

2

n

n

6

n+1

2.5

∞

P

n=1

4n

4

(

3+

2

n

)

n

2.6

∞

P

n=1

e

−n!

2.7

∞

P

n=1

2

2

n

n+1

n

n

2

2.8

∞

P

n=1

3

n2 −1

2

n2

√

n

2.9

∞

P

n=1

ln n

n

n

2.10

∞

P

n=1

√

n

√

en−1

2n

2.11

∞

P

n=1

arcsin

1

√

n

n

2.12

∞

P

n=1

1

arctg n!

n

2.13

∞

P

n=1

(n+5) 5

n

7

n

3

n+1

2.14

∞

P

n=1

3

n

n!

n

n

2.15

∞

P

n=1

n

2n

6

n

(n!)

2

2.16

∞

P

n=1

1·3·...·(2n−1)

3

n

n!

2.17

∞

P

n=1

(5

n

n!

(2n)

n+1

2.18

∞

P

n=1

(n+2)!

8

n

(n!)

2

2.19

∞

P

n=1

(2n)! 2

n

n

2n

2.20

∞

P

n=1

2

n

(1+2)(1+2

2

)...(1+2

n

)

2.21

∞

P

n=1

cos

1

n

2.22

∞

P

n=1

1 − cos

π
n

2.23

∞

P

n=1

cos

2 nπ

3

2

n

2.24

∞

P

n=1

sin

4

3

n

2.25

∞

P

n=1

3

√

n sin

2 1

n

2.26

∞

P

n=1

n tg

π

2

n+1

2.27

∞

P

n=1

3

√

n

1+

√

n

tg

1

√

n

2.28

∞

P

n=1

tg

3 2π

n

2.29

∞

P

n=1

n

4

n

( 2 + (−1)

n

)

2.30

∞

P

n=1

n

3

(

√

2+(−1)

n

)

n

3

n

2.31

∞

P

n=1

ln n

n

2.32

∞

P

n=1

ln n

2

n

2.33

∞

P

n=1

7n−1

3n

2

+8

2.34

∞

P

n=1

2n+2

n

2

(n+3)

2.35

∞

P

n=1

√

n+1−

√

n

n

2.36

∞

P

n=1

3

√

n+1

3

√

n

2.37

∞

P

n=1

4n

3

−1

(3n

2

+8)(5n

2

−1)

2.38

∞

P

n=1

n+1

√

n (n+2)

2.39

∞

P

n=1

3

√

n+1

√

n

3

√

2n−1

2.40

∞

P

n=1

1

√

3n+8

2.41

∞

P

n=1

1

√

4n

3

+n

2

−1

2.42

∞

P

n=1

3

√

n+2

n

√

n+n

4

√

n

2.43

∞

P

n=1

4

q

n+1

n

3

+3

2.44

∞

P

n=1

2n−3

√

n−12

n

2

+6

2.45

∞

P

n=2

1

n ln n

2.46

∞

P

n=2

1

n ln

2

n

2.47

∞

P

n=3

1

n ln n ln(ln n)

2.48

∞

P

n=1

e

−

√

n

√

n

2.49

∞

P

n=2

1+ln n

n

2.50

∞

P

n=2

1

n

4

√

ln n

2.51

∞

P

n=3

n

e

n

2.52

∞

P

n=1

arctg n

n

2

+1

Zad.3 Zbadaj zbieżność szeregów:

3.1

∞

P

n=1

(−1)

n

n

4

+4

3.2

∞

P

n=1

(−1)

n

1+

√

n+1

3.3

∞

P

n=1

cos nπ

n

2

+n

3.4

∞

P

n=1

(−1)

n+1

(n+2)

n

3

+2n+4

3.5

∞

P

n=1

(−1)

n

ln n

n

3.6

∞

P

n=1

(−1)

n+1

2

√

n−1

3.7

∞

P

n=1

(−1)

n

n

4

+4

3.8

∞

P

n=1

(−1)

n

n sin

1

n

3

3.9

∞

P

n=1

(−1)

n

6n−1
9n+4

n

3.10

∞

P

n=1

(−1)

n n!

n

n

3.11

∞

P

n=1

(−1)

n

10

n

n!

(2n)!

3.12

∞

P

n=1

(−7)

n

(n!)

2

sin

1

n

n

2n−1

3.13

∞

P

n=1

sin

nπ

6

n

4

3.14

∞

P

n=1

n cos n!

n

3

+3

3.15

∞

P

n=1

(2n)! sin

nπ

2

n

2n

3.16

∞

P

n=1

n

3n

cos n

(3n)!

1