Miejsce na identyfikacj´ szko∏y
Za rozwiàzanie
wszystkich zadaƒ
mo˝na otrzymaç
∏àcznie 50 punktów.
LISTOPAD
ROK 2008
KOD
ZDAJÑCEGO
PESEL ZDAJÑCEGO
Wpisuje zdajàcy przed rozpocz´ciem pracy
ARKUSZ PRÓBNEJ
MATURY Z OPERONEM
MATEMATYKA
POZIOM PODSTAWOWY
Czas pracy 120 minut
Instrukcja dla zdajàcego
1. Sprawdê, czy arkusz egzaminacyjny zawiera 14 stron (zada-
nia 1–11). Ewentualny brak zg∏oÊ przewodniczàcemu
zespo∏u nadzorujàcego egzamin.
2. Rozwiàzania zadaƒ i odpowiedzi zamieÊç w miejscu na to
przeznaczonym.
3. W rozwiàzaniach zadaƒ przedstaw tok rozumowania prowa-
dzàcy do ostatecznego wyniku.
4. Pisz czytelnie. U˝ywaj d∏ugopisu/pióra tylko z czarnym
tuszem/atramentem.
5. Nie u˝ywaj korektora, a b∏´dne zapisy przekreÊl.
6. Pami´taj, ˝e zapisy w brudnopisie nie podlegajà ocenie.
7. Obok ka˝dego zadania podana jest maksymalna liczba
punktów, którà mo˝esz uzyskaç za jego poprawne rozwià-
zanie.
8. Mo˝esz korzystaç z zestawu wzorów matematycznych, cyrkla
i linijki oraz kalkulatora.
˚yczymy powodzenia!
Arkusz opracowany przez Wydawnictwo Pedagogiczne OPERON.
Kopiowanie w ca∏oÊci lub we fragmentach bez zgody wydawcy zabronione. Wydawca zezwala na kopiowanie zadaƒ
przez dyrektorów szkó∏ bioràcych udzia∏ w programie Próbna Matura z OPERONEM.
dysleksja

2

3
Zadanie 1. (5 pkt)
Wyra˝enie
a
a
b
a
b
a
4
2
3
4
2
1
1
3
2
6
$
$
$
$
-
-
-
`
d
a
j
n
k
R
T
S
S
S
S
S
S
V
X
W
W
W
W
W
W
, gdzie , >
a b
0
, przedstaw w postaci iloczynu pot´g o wyk∏adni-
kach ca∏kowitych. Sprawdê, czy wartoÊç wyra˝enia dla a 3
4
1
=
-
i b 3
3
1
=
-
jest liczbà niewymiernà.
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”

4
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
Zadanie 2. (4 pkt)
Funkcja liniowa f okreÊlona jest wzorem ( )
f x
x
b
3
=
+
, dla x
R
! .
a) Wyznacz wspó∏czynnik b, wiedzàc, ˝e (
)
f x
x
2
3
5
-
=
-
.
b) Narysuj wykres funkcji f .
c) Sporzàdê wykres funkcji g, który jest obrazem wykresu funkcji f w przesuni´ciu o 2 jednostki
w gór´ wzd∏u˝ osi OY .
d) Podaj, dla jakich argumentów wartoÊci funkcji g sà ujemne.

5
Zadanie 3. (3 pkt)
Wielomian W okreÊlony jest wzorem ( )
W x
x
x
4
1
3
=
-
+
. Wyznacz wszystkie wartoÊci x spe∏niajàce
nierównoÊç (
) >
(
)
W x
W x
2
4
+
+
.
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”

6
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
Zadanie 4. (6 pkt)
Dany jest równoleg∏obok, którego obwód jest równy 50 cm. Stosunek d∏ugoÊci jego wysokoÊci wy-
nosi :
2 3
, a stosunek miar jego kàtów wewn´trznych jest równy :
1 2
. Oblicz d∏ugoÊci boków i wyso-
koÊci tego równoleg∏oboku. Wykonaj rysunek pomocniczy.

7
Zadanie 5. (3 pkt)
Oblicz wartoÊç wyra˝enia
sin
cos
sin
cos
x
x
x
x
2
3
-
+
, wiedzàc, ˝e
,
x
0
2
!
r
c
m
i x
tg
2
=
.
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
8
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
Zadanie 6. (4 pkt)
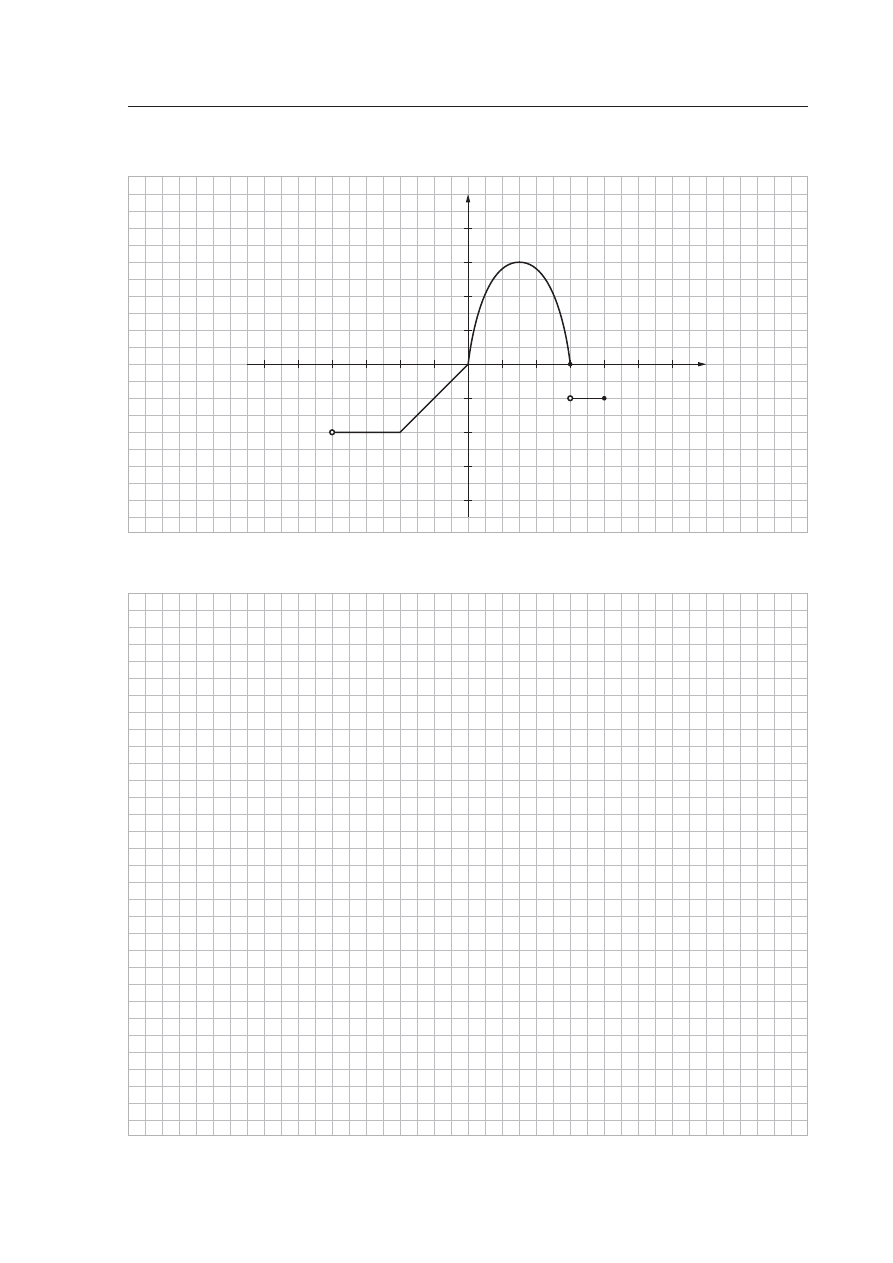
Na rysunku przedstawiony jest wykres funkcji f .
a) Podaj dziedzin´, zbiór wartoÊci i miejsca zerowe funkcji f .
b) Podaj maksymalne przedzia∏y, w których funkcja f jest sta∏a.
X
Y
1
– 4
– 3
– 2
– 1
2
3
4
– 6
– 5
– 4
– 3
– 2
– 1
2
1
3
4
5
6

9
Zadanie 7. (5 pkt)
Rozwià˝ równanie
...
x
2
6
10
200
+
+
+
+
=
, wiedzàc, ˝e jego lewa strona jest sumà ciàgu arytme-
tycznego.
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”

10
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
Zadanie 8. (5 pkt)
Punkty
,
A
3
1
= -
-
_
i
i
,
B
3 5
=
_
i
sà wierzcho∏kami trójkàta ABC. Wyznacz wspó∏rz´dne punktu C, wie-
dzàc, ˝e wysokoÊci tego trójkàta przecinajà si´ w punkcie
,
W
1 1
=
_
i
.

11
Zadanie 9. (6 pkt)
Funkcja f okreÊlona jest wzorem ( )
f x
x
x
c
3
9
2
=
-
+
, gdzie
.
c
R
!
Wyznacz wszystkie wartoÊci wspó∏-
czynnika c, dla których:
a) funkcja f nie ma miejsc zerowych,
b) jednym z miejsc zerowych funkcji f jest liczba 2,
c) wierzcho∏ek paraboli, która jest wykresem funkcji f , nale˝y do prostej o równaniu y x
=
.
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”

12
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
Zadanie 10. (4 pkt)
Rzucamy dwiema symetrycznymi kostkami w kszta∏cie czworoÊcianu foremnego o ponumerowa-
nych Êcianach od 1 do 4 i obliczamy sum´ otrzymanych oczek.
a) Skonstruuj tabel´, tak aby przedstawia∏a wszystkie mo˝liwe wyniki tego doÊwiadczenia.
b) Oblicz prawdopodobieƒstwo zdarzenia, ˝e suma wyrzuconych cyfr jest mniejsza od 5.

13
Zadanie 11. (5 pkt)
Dany jest ostros∏up prawid∏owy szeÊciokàtny, w którym d∏ugoÊç wysokoÊci jest równa
cm
2 3
. Kàt
mi´dzy Êcianà bocznà i p∏aszczyznà podstawy ma miar´ 60c. Sporzàdê rysunek pomocniczy. Oblicz
obj´toÊç i pole powierzchni bocznej tego ostros∏upa.
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”

14
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
BRUDNOPIS (nie podlega ocenie)
Wyszukiwarka
Podobne podstrony:
Matematyka listopad 2008
Matematyka listopad 2009
1 Sklad granulometryczny listopad 2008
więcej podobnych podstron