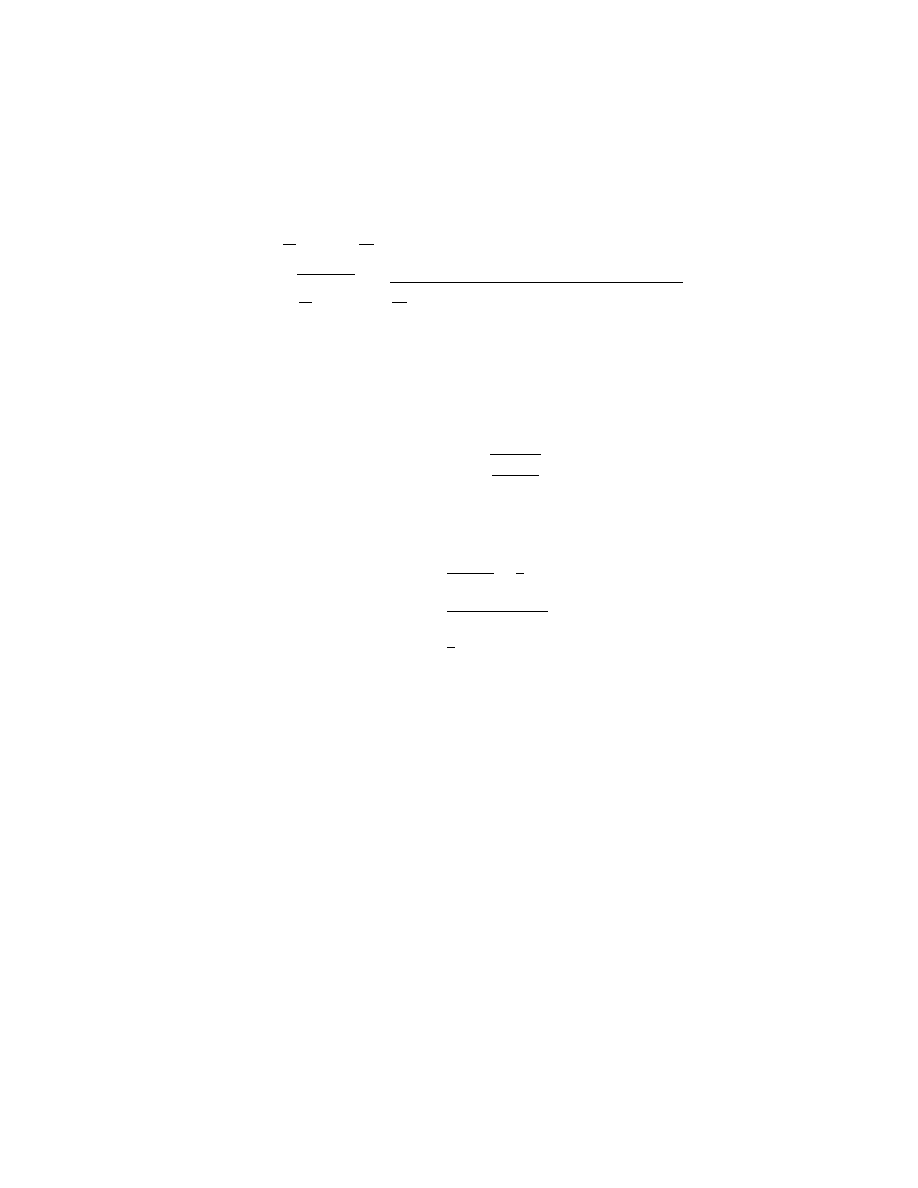
38.

(a) The average and rms speeds are as follows:

v

avg

=

1

N

N

i=1

v

i

=

1

10

[4(200 m/s) + 2(500 m/s) + 4(600 m/s)]= 420 m/s ,

v

rms

=

1

N

N

i=1

v

2

i

=

1

10

[4(200 m/s)

2

+ 2(500 m/s)

2

+ 4(600 m/s)

2

]= 458 m/s .

From these results, we see that v

rms

> v

avg

.

(b) One may check the validity of the inequality v

rms

≥ v

avg

for any speed distribution. For example,

we consider a set of ten particles divided into two groups of five particles each, with the first group
of particles moving at speed v

1

and the second group at v

2

where both v

1

and v

2

are positive-valued

(by the definition of speed). In this case, v

avg

= (v

1

+ v

2

) /2 and

v

rms

=

v

2

1

+ v

2

2

2

.

To show this must be greater than (or equal to) v

avg

we examine the difference in the squares of

the quantities:

v

2

rms

− v

2

avg

=

v

2

1

+ v

2

2

2

−

1

4

v

2

1

+ v

2

2

+ 2v

1

v

2

=

v

2

1

+ v

2

2

− 2v

1

v

2

4

=

1

4

(v

1

− v

2

)

2

≥ 0

which demonstrates that v

rms

≥ v

avg

in this situation.

(c) As one can infer from our manipulation in the previous part, we will obtain v

rms

= v

avg

if all speeds

are the same (if v

1

= v

2

in the previous part).