Ìîñêîâñêèé ôèçèêî-òåõíè÷åñêèé èíñòèòóò

(ãîñóäàðñòâåííûé óíèâåðñèòåò)

ÒÎËÊÎÂÛÉ ÑËÎÂÀÐÜ

ÏÎ ÒÅÎÐÅÒÈ×ÅÑÊÎÉ

ÌÅÕÀÍÈÊÅ

ÌÎÑÊÂÀ 2007

Ñîñòàâèòåëü Ã.Í. ßêîâåíêî

Ðåöåíçåíò

Äîöåíò Þ.È. Õàíóêàåâ

Òîëêîâûé ñëîâàðü ïî òåîðåòè÷åñêîé ìåõàíèêå /

Ñîñò. Ã.Í. ßêîâåíêî.. Ì.: ÌÔÒÈ, 2007. 68 ñ.

Öåëüþ èçäàíèÿ ÿâëÿåòñÿ íàâåäåíèå òåðìèíîëîãè÷åñêî-

ãî åäèíñòâà â ñðåäå èçó÷àþùèõ è ïðåïîäàþùèõ òåîðåòè-

÷åñêóþ ìåõàíèêó. Ïðèâåäåíû ôîðìóëèðîâêè îïðåäåëåíèé,

ïîíÿòèé, óòâåðæäåíèé òåîðåòè÷åñêîé è àíàëèòè÷åñêîé ìå-

õàíèêè. Ðàññìîòðåíèå îãðàíè÷åíî òåìàìè, âõîäÿùèìè â

ïðîãðàììó êóðñà Òåîðåòè÷åñêàÿ ìåõàíèêà ÌÔÒÈ.  êàæ-

äîé ñòàòüå äàþòñÿ ññûëêè íà ëèòåðàòóðíûå èñòî÷íèêè ñ

óêàçàíèåì ñòðàíèö.

Èçäàíèå áóäåò ïîëåçíî ñòóäåíòàì è ïðåïîäàâàòåëÿì,

èçó÷àþùèì èëè ïðåïîäàþùèì îáùóþ ôèçèêó è òåîðåòè-

÷åñêóþ ìåõàíèêó, à òàêæå ñìåæíûå äèñöèïëèíû àýðî è

ãèäðîìåõàíèêó, ñîïðîìàò, äèíàìèêó êîñìè÷åñêîãî ïîëåòà

è ò. ä. Ïîñîáèå áóäåò ïîëåçíî âñåì òåì, êòî ïî ðîäó ñâîèõ

çàíÿòèé äîëæåí èñïîëüçîâàòü è ïîíèìàòü òåðìèíîëîãèþ

òåîðåòè÷åñêîé ìåõàíèêè: íàó÷íûì ìåíåäæåðàì, ìàðêåòî-

ëîãàì íàó÷íî-òåõíè÷åñêîé ëèòåðàòóðû è ò. ä.

ÒÎËÊÎÂÛÉ ÑËÎÂÀÐÜ

ÏÎ ÒÅÎÐÅÒÈ×ÅÑÊÎÉ

ÌÅÕÀÍÈÊÅ

Ñîñòàâèòåëü ßêîâåíêî Ãåííàäèé Íèêîëàåâè÷

ÂÂÅÄÅÍÈÅ

Äëÿ êàæäîãî ÿâëåíèÿ æèçíè íàéä¼òñÿ

ïîñëîâèöà-ïîãîâîðêà, êîòîðàÿ ýòî ÿâëå-

íèå îäîáðÿåò, à òàêæå ïîñëîâèöà-

ïîãîâîðêà, êîòîðàÿ ýòî ÿâëåíèå îñóæ-

äàåò.  ýòîì è çàêëþ÷àåòñÿ íàðîäíàÿ

ìóäðîñòü.

Íàðîäíàÿ ìóäðîñòü

Ïðèâåä¼ì íåñêîëüêî ïðèìåðîâ ðàçíî÷òåíèé â òîëêîâàíèè

òåðìèíîâ òåîðåòè÷åñêîé ìåõàíèêè (ïîäðîáíîñòè â ñòàòüÿõ ñëî-

âàðÿ). Àìïëèòóäà, ÷àñòîòà, ôàçà ãàðìîíè÷åñêîãî êîëåáàíèÿ

[6, ÷. 1, ñ. 59], [8, ñ. 202], [13, ñ. 177], [23, ò. 1, ñ. 888],

[32, ñ. 848]. Âîçìîæíîå, äåéñòâèòåëüíîå, âèðòóàëüíîå ïåðåìå-

ùåíèå [1, ñ. 154], [7, ñ. 11], [22, ñ. 38], [25, ñ. 29], [36, ñ. 45]. Â

ñëîâàðå ïðèâåäåíû ôîðìóëèðîâêè îïðåäåëåíèé è óòâåðæäåíèé

òåîðåòè÷åñêîé ìåõàíèêè.  ñëó÷àå ðàçíî÷òåíèé äàíû ññûëêè

íà íåñêîëüêî âàðèàíòîâ. Â ññûëêàõ óêàçàíû ñòðàíèöû. Ðàñ-

ñìîòðåíèå îãðàíè÷åíî òåìàìè, òðàäèöèîííî âõîäÿùèìè â ïðî-

ãðàììó êóðñà Òåîðåòè÷åñêàÿ ìåõàíèêà ÌÔÒÈ. Ôîðìóëèðîâ-

êè ïî âîçìîæíîñòè ñîãëàñîâûâàëèñü ñ òåðìèíîëîãè÷åñêèìè

ñáîðíèêàìè [29, 31].

Ñîñòàâèòåëü áëàãîäàðèò êîëëåã ïî êàôåäðå òåîðåòè÷åñêîé

ìåõàíèêè ÌÔÒÈ çà ïîñòîÿííóþ ïîìîùü è ïîíèìàíèå âîñòðå-

áîâàííîñòè íàñòîÿùåãî ñëîâàðÿ.

Íåêîòîðûå îáîçíà÷åíèÿ:

˙x =

dx

dt

;

(·, ·)

ñêàëÿðíîå ïðîèçâåäåíèå;

[·, ·]

âåêòîðíîå ïðîèçâåäåíèå;

δ

kl

=

(

1,

åñëè k = l,

0,

åñëè k 6= l

ñèìâîë Êðîíåêåðà;

q = (q

1

, . . . , q

n

)

.

3

Àáñîëþòíàÿ ñêîðîñòü [1, ñ. 32], [37, ñ. 24]. Ñêîðîñòü â àá-

ñîëþòíîì äâèæåíèè îòíîñèòåëüíî ñèñòåìû îòñ÷¼òà.

Àáñîëþòíîå äâèæåíèå [1, ñ. 31], [37, ñ. 22]. Äâèæåíèå

îòíîñèòåëüíî ñèñòåìû îòñ÷¼òà.

Àáñîëþòíîå óñêîðåíèå [1, ñ. 33], [37, ñ. 24]. Óñêîðåíèå â

àáñîëþòíîì äâèæåíèè îòíîñèòåëüíî ñèñòåìû îòñ÷¼-

òà.

Àêòèâíûå ñèëû [8, ñ. 19], [36, ñ. 36]. Ñèëû F (t, r, ˙r), äëÿ êî-

òîðûõ èçâåñòíà çàâèñèìîñòü îò âðåìåíè t è ñîñòîÿíèÿ, è

íà ýòó çàâèñèìîñòü íàëîæåíèå èëè ñíÿòèå ìåõàíè÷åñêèõ

ñâÿçåé âëèÿíèå íå îêàçûâàþò.

Àëãåáðà êâàòåðíèîíîâ [13, ñ. 32], [33, ñ. 36],

[37, ñ. 24]. ×åòûð¼õìåðíîå âåêòîðíîå ïðîñòðàíñòâî ñ ýëå-

ìåíòàìè Λ è áàçèñîì i

0

, i

1

, i

2

, i

3

. Áàçèñíûé ýëåìåíò i

0

èãðàåò ðîëü åäèíèöû (Λ ◦ i

0

= i

0

◦ Λ = Λ

) , îí îòîæ-

äåñòâëÿåòñÿ ñ åäèíèöåé 1 è ïðè óìíîæåíèè îïóñêàåòñÿ:
Λ = λ

0

+

3

P

k=1

λ

k

i

k

. Äëÿ ïðî÷èõ áàçèñíûõ ýëåìåíòîâ

(k, l

=

1, 3

) â òàáëèöå óìíîæåíèÿ ïðèíèìàåòñÿ

i

k

◦ i

l

=

(

−1,

åñëè k = l,

[i

k

, i

l

] ,

åñëè k 6= l.

Àìïëèòóäà ãàðìîíè÷åñêîãî êîëåáàíèÿ [6, ñ. 59],

[32, ñ. 110]. Âåëè÷èíà A â ãàðìîíè÷åñêîì êîëåáàíèè
x = A sin (ωt + α)

. Èíîãäà àìïëèòóäîé íàçûâàþò âåëè-

÷èíó |A| [8, ñ. 202], [23, ò. 1, ñ. 888].

Àìïëèòóäíàÿ ÷àñòîòíàÿ õàðàêòåðèñòèêà [1, ñ. 252],

[12, ñ. 45], [37, ñ. 132]. Çàâèñèìîñòü ìîäóëÿ
R

jk

(Ω) = |W

jk

(iΩ)|

àìïëèòóäíî-ôàçîâîé õàðàêòåðèñòè-

êè W

jk

(iΩ) = R

jk

(Ω) e

iψ

jk

(Ω)

îò ïåðåìåííîé Ω.

4

Àìïëèòóäíî-ôàçîâàÿ

÷àñòîòíàÿ

õàðàêòåðèñòèêà

[1, ñ. 251], [12, ñ. 45], [37, ñ. 131]. Ó ëèíåéíîé îä-

íîðîäíîé ñèñòåìû A¨q + B ˙q + Cq = 0 (A, B, C = const)

óðàâíåíèé Ëàãðàíæà îòûñêèâàåòñÿ ðåøåíèå â âèäå q =
ue

iΩt

. Ïîñëå ñîêðàùåíèÿ íà ýêñïîíåíòó, îñòà¼òñÿ ëèíåé-

íàÿ îäíîðîäíàÿ àëãåáðàè÷åñêàÿ ñèñòåìû óðàâíåíèé îò-

íîñèòåëüíî àìïëèòóä u. Àìïëèòóäíî-ôàçîâàÿ õàðàêòå-

ðèñòèêà W

jk

(iΩ)

ýòî äðîáü, â çíàìåíàòåëå êîòîðîé

íàõîäèòñÿ îïðåäåëèòåëü ìàòðèöû êîýôôèöèåíòîâ ñèñòå-

ìû, à â ÷èñëèòåëå àëãåáðàè÷åñêîå äîïîëíåíèå ýëåìåíòà

ñ íîìåðîì jk.

Àñèìïòîòè÷åñêàÿ

óñòîé÷èâîñòü

ïî

Ëÿïóíîâó

[8, ñ. 174], [36, ñ. 109]. Ðåøåíèå x = 0 ñèñòåìû â

íîðìàëüíîì âèäå ˙x = ϕ (t, x) , x ∈ R

n

, àñèìïòîòè÷åñêè

óñòîé÷èâî ïî Ëÿïóíîâó, åñëè îíî: 1) óñòîé÷èâî ïî Ëÿïó-

íîâó; 2) ñóùåñòâóåò òàêàÿ ∆-îêðåñòíîñòü òî÷êè x = 0 (îá-

ëàñòü ïðèòÿæåíèÿ), ÷òî äëÿ îáùåãî ðåøåíèÿ x (t, t

0

, x

0

)

âûïîëíÿåòñÿ: {|x

0

| < ∆} ⇒ { lim

t→∞

x (t, t

0

, x

0

) = 0}

.

Áèíå óðàâíåíèå (óðàâíåíèå Áèíå, âòîðàÿ ôîðìóëà Áèíå)

[10, ñ. 191], [13, ñ. 78], [37, ñ. 65]. Óðàâíåíèå äëÿ òðà-

åêòîðèé â öåíòðàëüíîì ïîëå: u

00

+ u = −r

2

f /mc

2

, ãäå r,

ϕ

ïîëÿðíûå êîîðäèíàòû, u = 1/r, u

00

= d

2

u/dϕ

2

, f

âåëè÷èíà öåíòðàëüíîé ñèëû, c ïðèâåä¼ííûé ìîìåíò

èìïóëüñà.

Áèíîðìàëè îðò. Ñì. îðò áèíîðìàëè.
Âàëåíòíîñòü [8, ñ. 131], [36, ñ. 193]. ×èñëî c 6= 0 â îñíîâ-

íîì êðèòåðèè êàíîíè÷íîñòè ïðåîáðàçîâàíèÿ ãàìèëüòî-

íîâûõ ïåðåìåííûõ.

Âàðèàöèîííàÿ ñèììåòðèÿ (í¼òåðîâñêàÿ ñèììåòðèÿ)

[15, ñ. 128][24, ñ. 332], [36, ñ. 151]. Íåîñîáåííîå ïðåîá-

ðàçîâàíèå ïåðåìåííûõ t, q ↔ bt, bq, ñâÿçàííîå ñ ôóíêöèåé

5

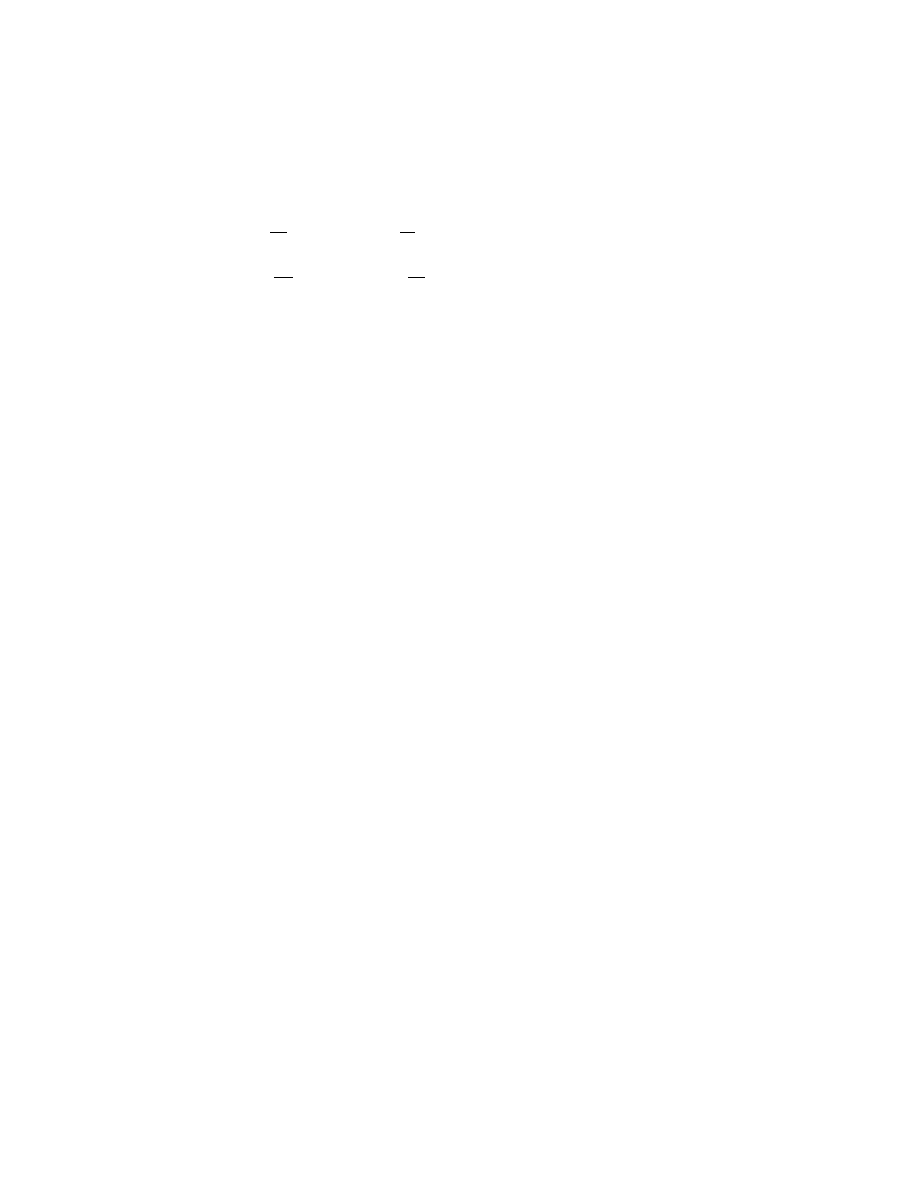
Ëàãðàíæà

L (t, q, ˙q)

ñëåäóþùèì

îáðàçîì

L

µ

b

t, b

q,

db

q

db

t

¶

= L (t, q, ˙q)

dt
db

t

(èëè â ñèììåòðè÷íîì âèäå

L

Ã

_

t ,

_

q ,

d

_

q

d

_

t

!

d

_

t = L

µ

t, q,

dq

dt

¶

dt

).

Âàðèàöèîííûé ïðèíöèï Ãàìèëüòîíà [1, ñ. 286],

[17, ñ. 190] (íà÷àëî Ãàìèëüòîíà [1, ñ. 287], ïðèíöèï

Ãàìèëüòîíà [8, ñ. 92], [25, ñ. 48] [36, ñ. 144], ïðèíöèï

Ãàìèëüòîíà

-

Îñòðîãðàäñêîãî

[19, ñ. 645], [22, ñ. 474], ïðèíöèï ñòàöèîíàðíîãî

äåéñòâèÿ

Ãàìèëüòîíà

[5,

ñ.

191],

[6, ÷. II, ñ. 262], [10, ñ. 446]. Ïóòü ˜q(t) â ðàñøèðåííîì

êîîðäèíàòíîì ïðîñòðàíñòâå ÿâëÿåòñÿ ïðÿìûì â òîì è

òîëüêî â òîì ñëó÷àå, åñëè ïðè ëþáîì âàðüèðîâàíèè q (t, α)

ïðè íåèçìåííûõ ãðàíè÷íûõ òî÷êàõ äëÿ âàðèàöèè äåé-

ñòâèÿ

ïî

Ãàìèëüòîíó

W (α)

âûïîëíÿåòñÿ

δW |

α=0

= ∂W/∂α

¯

¯

¯

α=0

δα = 0

.

Âàðüèðîâàíèå ôóíêöèè (ïðîâàðüèðîâàòü ôóíêöèþ)

[36, ñ. 144]. Âêëþ÷åíèå ôóíêöèè ˜q(t) â ãëàäêîå ñåìåé-

ñòâî ôóíêöèé q (t, α) (q (t, 0) = ˜q(t)).

Âàðèàöèÿ ôóíêöèè [1, ñ. 287], [17, ñ. 190]. Äèôôåðåíöèàë

ïðîâàðüèðîâàííîé ôóíêöèè ïî ïàðàìåòðó α.

Âåêîâîå óðàâíåíèå (óðàâíåíèå ÷àñòîò) [1, ñ. 243],

[36, ñ. 100]. Ìíîãî÷ëåííîå óðàâíåíèå äëÿ ðàçðåø¼ííûõ

êðóãîâûõ ÷àñòîò ãàðìîíè÷åñêèõ êîëåáàíèé ïðè ðåøåíèè

çàäà÷è ìàëûõ (ëèíåéíûõ) êîëåáàíèé.

Âåêòîð êðèâèçíû òðàåêòîðèè [1, ñ. 17], [37, ñ. 7]. Âû÷èñ-

ëÿåòñÿ ïî ôîðìóëå K = dτ /ds = Kn = n/ρ, ãäå τ îðò

êàñàòåëüíîé, n îðò íîðìàëè, ρ ðàäèóñ êðèâèçíû, s

äëèíà äóãè òðàåêòîðèè.

6

Âåêòîðíàÿ ÷àñòü êâàòåðíèîíà [13, ñ. 32], [33, ñ. 37],

[37, ñ. 24]. ×àñòü λ = λ

1

i

1

+ λ

2

i

2

+ λ

3

i

3

êâàòåðíèîíà

Λ = λ

0

+ λ

1

i

1

+ λ

2

i

2

+ λ

3

i

3

= λ

0

+ λ

.

Âåêòîðíûå èíâàðèàíòû [1, ñ. 361], [37, ñ. 38]. Ãëàâíûé

âåêòîð R è ãëàâíûé ìîìåíò M

O

ìíîæåñòâà ñêîëüçÿùèõ

âåêòîðîâ.

Âåêòîðíûé íóëü [1, ñ. 358], [37, ñ. 34]. Ïàðà ñ íóëåâûì

ïëå÷îì.

Âèíò [1, ñ. 364], [37, ñ. 39]. Ñîâîêóïíîñòü: ïðÿìàÿ ëèíèÿ

îñü âèíòà; ðàñïîëîæåííûé íà îñè âèíòà ñêîëüçÿùèé

âåêòîð R; ðàñïîëîæåííûé íà îñè âèíòà ìîìåíò M

O

îò-

íîñèòåëüíî òî÷êè Î îñè âèíòà.

Âèðòóàëüíîå

ïåðåìåùåíèå

òî÷êè

[1,

ñ.

154],

[5, ñ. 15], [36, ñ. 15]. Äèôôåðåíöèàë ðàäèóñ-âåêòîðà, íå

ïðîòèâîðå÷àùèé óðàâíåíèÿì ìåõàíè÷åñêèõ ñâÿçåé ïðè

ôèêñèðîâàííîì â óðàâíåíèÿõ âðåìåíè t.

Âíåøíåå

âîçäåéñòâèå

(âõîäíîå

âîçäåéñòâèå)

[36, ñ. 129]. Îáîáù¼ííàÿ ñèëà, çàâèñÿùàÿ òîëüêî îò âðå-

ìåíè t. Âíåøíèå ñèëû [1, ñ. 58], [37, ñ. 50]. Ñèëû,
äåéñòâóþùèå íà òî÷êè ñèñòåìû ìàòåðèàëüíûõ òî÷åê, è

âûçâàííûå âçàèìîäåéñòâèåì ñ òî÷êàìè, íå ïðèíàäëåæà-

ùèìè ñèñòåìå.

Âíóòðåííèå ñèëû [1, ñ. 57], [37, ñ. 50]. Ñèëû âçàèìîäåé-

ñòâèÿ ìåæäó äâóìÿ òî÷êàìè, ïðèíàäëåæàùèìè ñèñòåìå

ìàòåðèàëüíûõ òî÷åê.

Âîçìîæíûå ïåðåìåùåíèÿ [1, ñ. 154], [36, ñ. 45]. Äèôôå-

ðåíöèàë ðàäèóñ-âåêòîðà, íå ïðîòèâîðå÷àùèé óðàâíåíèÿì

ìåõàíè÷åñêèõ ñâÿçåé. Äèôôåðåíöèàë ðàäèóñ-âåêòîðà, ñî-

ãëàñîâàííûé ñ âîçìîæíîé ñêîðîñòüþ.

7

Âîçìîæíûå ñêîðîñòè [1, ñ. 154], [36, ñ. 45]. Ñêîðîñòè òî÷åê

ñèñòåìû ïðè äâèæåíèè, íå íàðóøàþùåì íàëîæåííûå íà

ñèñòåìó ìåõàíè÷åñêèå ñâÿçè.

Âòîðàÿ ôîðìóëà Áèíå Ñì. Áèíå óðàâíåíèå.
Âòîðîé çàêîí Êåïëåðà [1, ñ. 93], [37, ñ. 64]. Ïðè äâèæåíèè

ïîä âîçäåéñòâèåì öåíòðàëüíîé ñèëû ïëîùàäü çàìåòàå-

ìàÿ ðàäèóñîì-âåêòîðîì, ïðîïîðöèîíàëüíà âðåìåíè äâè-

æåíèÿ.

Âòîðîé

çàêîí

Íüþòîíà

(óðàâíåíèå

Íüþòîíà)

[1, ñ. 57], [37, ñ. 48]. Óðàâíåíèå mW = F, ãäå m

ìàññà ìàòåðèàëüíîé òî÷êè, W óñêîðåíèå òî÷êè, F

ñèëà, äåéñòâóþùàÿ íà òî÷êó.

Âõîäíîå âîçäåéñòâèå. Òî æå, ÷òî âíåøíåå âîçäåéñòâèå.
Âûíóæäåííàÿ ðåãóëÿðíàÿ ïðåöåññèÿ òâ¼ðäîãî òåëà ñ

íåïîäâèæíîé òî÷êîé [1, ñ. 207], [37, ñ. 106]. Ðåãóëÿð-

íàÿ ïðåöåññèÿ ïîä âîçäåéñòâèåì ïðèëîæåííûõ ê òâ¼ð-

äîìó òåëó ñèë. Äëÿ äâèæåíèÿ ñ çàäàííûìè ïàðàìåòðà-

ìè ðåãóëÿðíîé ïðåöåññèè (óãëîâàÿ ñêîðîñòü ñîáñòâåííî-

ãî âðàùåíèÿ ω

1

, óãëîâàÿ ñêîðîñòü ïðåöåññèè ω

2

, óãîë íó-

òàöèè θ) ìîìåíò ïðèëîæåííûõ ñèë îòíîñèòåëüíî íåïî-

äâèæíîé òî÷êè O ðàâåí

M

O

= [ω

2

, ω

1

]

½

C +

ω

2

ω

1

(C − A) cos θ

¾

,

ãäå C ìîìåíò èíåðöèè îòíîñèòåëüíî îñè äèíàìè÷å-

ñêîé ñèììåòðèè, A ìîìåíò èíåðöèè îòíîñèòåëüíî

îñè, ðàñïîëîæåííîé â ýêâàòîðèàëüíîé ïëîñêîñòè.

Âûíóæäåííîå äâèæåíèå (âûõîä ñèñòåìû, îòêëèê ñè-

ñòåìû, ðåàêöèÿ ñèñòåìû, óñòàíîâèâøèéñÿ ïðîöåññ)

[1, ñ. 248], [36, ñ. 129]. Äâèæåíèå, âûçâàííîå âíåøíèì

(âõîäíûì) âîçäåéñòâèåì, ïîñëå çàòóõàíèÿ âëèÿíèÿ íà-

÷àëüíîãî ñîñòîÿíèÿ.

8

Âûõîä ñèñòåìû. Òî æå, ÷òî âûíóæäåííîå äâèæåíèå.
Ãàìèëüòîíèàí (ôóíêöèÿ Ãàìèëüòîíà) [1, ñ. 269],

[36, ñ. 136]. Ôóíêöèÿ H (t, q, p) ãàìèëüòîíîâûõ ïåðåìåí-

íûõ, êîòîðàÿ îïðåäåëÿåò ïðàâóþ ÷àñòü ãàìèëüòîíîâîé

ñèñòåìû. Ãàìèëüòîíèàí ñâÿçàí ñ ëàãðàíæèàíîì L(t, q, ˙q)
ñëåäóþùèì îáðàçîì: H =

n

P

i=1

p

i

˙q

i

− L

.

Ãàìèëüòîíîâà ñèñòåìà (óðàâíåíèÿ Ãàìèëüòîíà, êàíîíè-

÷åñêèå óðàâíåíèÿ Ãàìèëüòîíà) [1, ñ. 270],

[36, ñ. 136]. Ñèñòåìà îáûêíîâåííûõ äèôôåðåíöèàëüíûõ

óðàâíåíèé â íîðìàëüíîì âèäå

˙q

i

=

∂H

∂p

i

,

˙p

i

= −

∂H

∂q

i

.

Ïðàâàÿ ÷àñòü ñèñòåìû îïðåäåëåíà ôóíêöèåé Ãàìèëüòîíà

(ãàìèëüòîíèàíîì) H (t, q, p).

Ãàìèëüòîíîâû ïåðåìåííûå (ïåðåìåííûå Ãàìèëüòîíà)

[1, ñ. 268], [36, ñ. 135]. Ñîâîêóïíîñòü ïåðåìåííûõ: âðå-

ìÿ t, îáîáùåííûå êîîðäèíàòû q

i

, îáîáùåííûå èìïóëü-

ñû p

i

.

Ãàðìîíè÷åñêîå âîçäåéñòâèå [1, ñ. 249], [36, ñ. 132]. Âíåø-

íåå (âõîäíîå) ñèíóñîèäàëüíîå âîçäåéñòâèå

x = A sin (ωt + α)

ñ íåêîòîðûìè àìïëèòóäîé A, êðóãîâîé ÷àñòîòîé ω è íà-

÷àëüíîé ôàçîé α.

Ãàðìîíè÷åñêîå

(ñèíóñîèäàëüíîå)

êîëåáàíèå

[6, ÷. I, ñ. 59], [23, ò. 1, ñ. 888] [32, ñ. 110]. Èçìå-

íåíèå êîîðäèíàòû ïî çàêîíó x = A sin (ωt + α), ãäå A

àìïëèòóäà, ω êðóãîâàÿ (óãëîâàÿ, öèêëè÷åñêàÿ) ÷àñòî-

òà, α íà÷àëüíàÿ ôàçà.

Ãåîìåòðè÷åñêàÿ ñâÿçü (ãîëîíîìíàÿ ñâÿçü, êîíå÷íàÿ

ñâÿçü) [8, ñ. 12], [36, ñ. 21]. Ìåõàíè÷åñêàÿ óäåðæèâà-

9

þùàÿ ñâÿçü f (t, r

1

, . . . ,

r

N

) = 0

, óðàâíåíèå êîòîðîé ïðåä-

ñòàâèìî â âèäå ôóíêöèè îò âðåìåíè t è îò ïîëîæåíèÿ

r

1

, . . . ,

r

N

òî÷åê ñèñòåìû.

Ãåîìåòðèÿ ìàññ òâåðäîãî òåëà [1, ñ. 178], [37, ñ. 92]. Èçó-

÷åíèå ìîìåíòîâ èíåðöèè òâ¼ðäîãî òåëà îòíîñèòåëüíî

ïðîèçâîëüíûõ îñåé.

Ãèðîäèí [35, ñ. 189, ñ. 192]. Ðàçâîðà÷èâàþò ñòàíöèþ è óäåð-

æèâàþò å¼ â íóæíîì ïîëîæåíèè èñïîëíèòåëüíûå ìåõà-

íèçìû: ... òÿæåëûå âîë÷êè-ãèðîñêîïû, íàçûâàåìûå ãèðî-

äèíàìè (îò ãðå÷. ãèðîñ è äèíàìèñ ñèëà). Îñü ðàñ-

êðó÷åííîãî âîë÷êà ñòðåìèòñÿ ñîõðàíèòü ñâî¼ ïîëîæåíèå

â ïðîñòðàíñòâå, è äîñòàòî÷íî ìàññèâíûé ãèðîäèí ïðåïÿò-

ñòâóåò ïîâîðîòó âñåé êîñìè÷åñêîé ñòàíöèè.

Ãèðîñêîï Òâ¼ðäîå òåëî, äâèæóùååñÿ âîêðóã ôèêñèðîâàííîé

â í¼ì òî÷êè, äëÿ êîòîðîãî ýëëèïñîèä èíåðöèè ÿâëÿåòñÿ

ýëëèïñîèäîì âðàùåíèÿ [22, ñ. 206]. Â øèðîêîì ñìûñëå

ñëîâà òâ¼ðäîå òåëî, èìåþùåå ïðåèìóùåñòâåííîå âðà-

ùåíèå âîêðóã êàêîé-ëèáî îñè.  áîëåå óçêîì çíà÷åíèè

áûñòðî âðàùàþùèéñÿ ðîòîð [16, ñ. 87]. Äèíàìè÷åñêè

ñèììåòðè÷íîå òâ¼ðäîå òåëî, èìåþùåå îäíó íåïîäâèæíóþ

òî÷êó è äîñòàòî÷íî áîëüøîé ñîáñòâåííûé êèíåòè÷åñêèé

ìîìåíò [13, ñ. 92].

Ãèðîñêîïè÷åñêàÿ ìåõàíè÷åñêàÿ ñèñòåìà [1, ñ. 148], [36,

ñ. 52]. Ìåõàíè÷åñêàÿ ñèñòåìà íàçûâàåòñÿ ãèðîñêîïè÷å-

ñêîé ïðè âûïîëíåíèè ñëåäóþùèõ óñëîâèé: ñèñòåìà ñòà-

öèîíàðíî çàäàíà; ïîòåíöèàëüíàÿ ýíåðãèÿ çàâèñèò òîëüêî

îò îáîáù¼ííûõ êîîðäèíàò; ìîùíîñòü íåïîòåíöèàëüíûõ

ñèë ðàâíà íóëþ.

Ãèðîñòàò [21, ñ. 179], [38, ñ. 227]. Ñîâîêóïíîñòü òâ¼ðäûõ

òåë: òåëî ñ íåïîäâèæíîé òî÷êîé; ðîòîðû ñ äèíàìè÷åñêîé

ñèììåòðèåé, âðàùàþùèåñÿ ñ ïîñòîÿííîé óãëîâîé ñêîðî-

ñòüþ âîêðóã ñâÿçàííûõ ñ òåëîì îñåé äèíàìè÷åñêîé ñèì-

ìåòðèè.

10

Ãëàâíàÿ îñü èíåðöèè â òî÷êå Î

[1, ñ. 183],

[37, ñ. 95]. Îñü ñèììåòðèè ýëëèïñîèäà èíåðöèè â òî÷-

êå Î. Öåíòðîáåæíûå ìîìåíòû èíåðöèè ñ óïîìèíàíèåì

ýòîé îñè ðàíû íóëþ.

Ãëàâíàÿ ôóíêöèÿ Ãàìèëüòîíà W

¡

t, q, q

0

¢

[8, ñ. 139],

[36, ñ. 208]. Äåéñòâèå ïî Ãàìèëüòîíó

W =

t

R

t

0

L

¡

s, q(s, q

0

, p

0

), ˙q(s, q

0

, p

0

)

¢

ds

âû÷èñëÿåòñÿ íà îáùåì ðåøåíèè q

¡

t, q

0

, p

0

¢

, p

¡

t, q

0

, p

0

¢

óðàâ-

íåíèé Ãàìèëüòîíà.  ðåçóëüòàò âû÷èñëåíèÿ ïîäñòàâëÿåò-

ñÿ íàéäåííàÿ èç îáùåãî ðåøåíèÿ âåêòîð-ôóíêöèÿ
p

0

= p

0

¡

t, q, q

0

¢

.

Ãëàâíàÿ öåíòðàëüíàÿ îñü èíåðöèè [1, ñ. 179],

[37, ñ. 96]. Îñü ñèììåòðèè ýëëèïñîèäà èíåðöèè â öåí-

òðå ìàññ (öåíòðå èíåðöèè) Ñ òâ¼ðäîãî òåëà.

Ãëàâíîå êîëåáàíèå [1, ñ. 245], [36, ñ. 100]. Âñå êîîðäèíàòû

èçìåíÿþòñÿ ñèíóñîèäàëüíî ñ îäèíàêîâûìè ÷àñòîòîé è

íà÷àëüíîé

ôàçîé,

íî,

âîçìîæíî,

ñ

ðàçíûìè

àìïëèòóäàìè.

Ãëàâíûå

êîîðäèíàòû

(íîðìàëüíûå

êîîðäèíàòû)

[1, ñ. 243], [36, ñ. 104]. Êîîðäèíàòû θ

i

, â êîòîðûõ êèíå-

òè÷åñêàÿ ýíåðãèÿ èìååò âèä T =

1
2

n

X

i=1

˙θ

2

i

, à ïîòåíöèàëü-

íàÿ Π =

1
2

n

X

i=1

r

i

θ

2

i

, r

i

=

const.

Ãëàâíûé âåêòîð R [1, ñ. 351], [30, ñ. 19], [37, ñ. 37]. Õàðàê-

òåðèñòèêà R =

N

P

i=1

a

i

ìíîæåñòâà âåêòîðîâ {a

i

}

ðåçóëü-

òàò òàêîãî ïàðàëëåëüíîãî ïåðåíîñà âåêòîðîâ, ÷òî ó íèõ

ñîâïàäàþò íà÷àëüíûå òî÷êè, è ïîñëåäóþùåãî èõ ñëîæå-

íèÿ.

11

Ãëàâíûé

ìîìåíò M

O

îòíîñèòåëüíî

òî÷êè

Î

[1,

ñ.

353],

[37,

ñ.

38].

Õàðàêòåðèñòèêà

M

O

=

N

P

i=1

m

O

(a

i

)

ìíîæåñòâà âåêòîðîâ {a

i

}

ìîìåíòû

m

O

(a

i

)

îòäåëüíûõ âåêòîðîâ îòêëàäûâàþòñÿ îò òî÷êè Î,

çàòåì ñêëàäûâàþòñÿ.

Ãîäîãðàô Ìèõàéëîâà [1, ñ. 229], [36, ñ. 119].  ìíîãî÷ëåí

f (λ)

ïîäñòàâëÿåòñÿ âìåñòî ïåðåìåííîé λ ìíèìàÿ ïåðå-

ìåííàÿ iω, çàòåì âûäåëÿþòñÿ äåéñòâèòåëüíàÿ è ìíèìàÿ

÷àñòè f (iω) = u (ω) + iv (ω), è ïðè èçìåíåíèè 0 6 ω < ∞

íà êîìïëåêñíîé ïëîñêîñòè (u, v) èçîáðàæàåòñÿ êðèâàÿ.

Ãîëîíîìíàÿ

ìåõàíè÷åñêàÿ

ñâÿçü

[1,

ñ.

153],

[36, ñ. 41]. Òî æå, ÷òî ãåîìåòðè÷åñêàÿ ñâÿçü.

Ãîëîíîìíàÿ ñèñòåìà [1, ñ. 153], [36, ñ. 41]. Ìåõàíè÷åñêàÿ

ñèñòåìà, íà êîòîðóþ íàëîæåíû ãåîìåòðè÷åñêèå (ãîëî-

íîìíûå, êîíå÷íûå) ñâÿçè.

Ãðóïïà

âàðèàöèîííûõ

ñèììåòðèé

[24,

ñ.

327],

[36, ñ. 152]. Ãðóïïà ïðåîáðàçîâàíèé, âñå ïðåîáðàçîâàíèÿ

êîòîðîé âàðèàöèîííûå ñèììåòðèè.

Ãþéãåíñà Õ., Øòåéíåðà ß. òåîðåìà [1, ñ. 178],

[37, ñ. 96]. Ìîìåíòû èíåðöèè I, I

C

òâ¼ðäîãî òåëà îòíî-

ñèòåëüíî ïàðàëëåëüíûõ îñåé, îäíà èç êîòîðûõ ïðîõîäèò

÷åðåç öåíòð ìàññ C òåëà, ñâÿçàíû ôîðìóëîé I = I

C

+md

2

,

ãäå m ìàññà òåëà, d ðàññòîÿíèå ìåæäó îñÿìè.

Äåéñòâèå ïî Ãàìèëüòîíó [1, ñ. 283], [36, ñ. 145]. Ôóíêöè-

îíàë W =

t

1

R

t

0

L (t, q, ˙q) |

q=q(t)

dt

, êîòîðûé ñòàâèò â ñîîòâåò-

ñòâèå ôóíêöèè q (t), îïðåäåë¼ííîé íà èíòåðâàëå
[t

0

, t

1

]

, ÷èñëî (L (t, q, ˙q) ôóíêöèÿ Ëàãðàíæà).

Äåéñòâèå ïî Ëàãðàíæó [1, ñ. 343], [36, ñ. 178]. Ôóíêöèîíàë

W

∗

=

q

1

1

R

q

0

1

P (t, q, q

0

) |

q=q(q

1

)

dq

1

, êîòîðûé ñòàâèò â ñîîòâåò-

12

ñòâèå ôóíêöèè q (q

1

)

, îïðåäåë¼ííîé íà èíòåðâàëå

£

q

0

1

, q

1

1

¤

,

÷èñëî (P (t, q, q

0

)

ôóíêöèÿ ßêîáè).

Äåéñòâèòåëüíàÿ

÷àñòîòíàÿ

õàðàêòåðèñòèêà

[12, ñ. 45], [36, ñ. 131]. Çàâèñèìîñòü äåéñòâèòåëüíîé

÷àñòè P

jk

(Ω) = ReW

jk

(iΩ)

àìïëèòóäíî-ôàçîâîé õàðàê-

òåðèñòèêè W

jk

(iΩ) = P

jk

(Ω) + iS

jk

(Ω)

îò ïåðåìåííîé

Ω

.

Äåêàðòîâû

êîîðäèíàòû

ìàòåðèàëüíîé

òî÷êè

[30, ñ. 43], [36, ñ. 9]. Êîýôôèöèåíòû x

k

ðàçëîæåíèÿ

ðàäèóñà-âåêòîðà r ïî îðòàì i

k

, ñâÿçàííîãî ñ ñèñòåìîé

îòñ÷¼òà áàçèñà: r =

3

P

k=1

x

k

i

k

.

Äèâåðãåíòíàÿ ñèììåòðèÿ [24, ñ. 358], [36, ñ. 151]. Íåîñî-

áåííîå ïðåîáðàçîâàíèå ïåðåìåííûõ t, q ↔

_

ˆt,

_

q

, ñâÿçàí-

íîå ñ ôóíêöèåé Ëàãðàíæà L (t, q, ˙q) ñëåäóþùèì îáðàçîì

L

Ã

_

t ,

_

q ,

d

_

q

d

_

t

!

+

df

³

_

t ,

_

q

´

d

_

t

= L (t, q, ˙q)

dt

d

_

t

èëè â ñèììåò-

ðè÷íîì âèäå

L

Ã

_

t ,

_

q ,

d

_

q

d

_

t

!

d

_

t + df

³

_

t ,

_

q

´

= L

µ

t, q,

dq

dt

¶

dt

.

Äèíàìè÷åñêàÿ ñèììåòðèÿ â òî÷êå Î

[1, ñ. 200],

[37, ñ. 96]. Ó òâ¼ðäîãî òåëà â äàííîé òî÷êå åñòü îñü äè-

íàìè÷åñêîé ñèììåòðèè.

Äèíàìè÷åñêèå

óðàâíåíèÿ

Ýéëåðà

[1,

ñ.

197],

[37, ñ. 100]. Óðàâíåíèÿ äâèæåíèÿ òâ¼ðäîãî òåëà ñ íåïî-

äâèæíîé òî÷êîé Î:

A ˙p + (C − B) qr = M

1

,

B ˙q + (A − C) pr = M

2

,

C ˙r + (B − C) pq = M

3

,

ãäå A, B, C ìîìåíòû èíåðöèè îòíîñèòåëüíî ãëàâíûõ

13

îñåé èíåðöèè â òî÷êå Î, p, q, r ïðîåêöèè óãëîâîé ñêî-

ðîñòè íà ãëàâíûå îñè èíåðöèè, M

1

, M

2

, M

3

ïðîåêöèè

ãëàâíîãî ìîìåíòà ñèë îòíîñèòåëüíî òî÷êè Î.

Äèññèïàòèâíàÿ ìåõàíè÷åñêàÿ ñèñòåìà [1, ñ. 149],

[36, ñ. 54]. Ñèñòåìà íàçûâàåòñÿ äèññèïàòèâíîé ïðè âû-

ïîëíåíèè ñëåäóþùèõ óñëîâèé: ñèñòåìà ñòàöèîíàðíî çà-

äàíà; ïîòåíöèàëüíàÿ ýíåðãèÿ çàâèñèò òîëüêî îò îáîáù¼í-

íûõ êîîðäèíàò; ìîùíîñòü íåïîòåíöèàëüíûõ ñèë íåïîëî-

æèòåëüíà. Ïðè âûïîëíåíèè áîëåå ñòðîãîãî óñëîâèÿ: ìîù-

íîñòü íåïîòåíöèàëüíûõ ñèë îòðèöàòåëüíà, åñëè äëÿ îáîá-

ù¼ííûõ ñêîðîñòåé ñïðàâåäëèâî ˙q

2

1

+ . . . + ˙q

2

n

6= 0

, ñè-

ñòåìà íàçûâàåòñÿ îïðåäåë¼ííî-äèññèïàòèâíîé.

Äèññèïàòèâíàÿ ôóíêöèÿ Ðåëåÿ Φ (t, q, ˙q) [1, ñ. 216],

[5, ñ. 59], [36, ñ. 55]. Êâàäðàòè÷íàÿ ôîðìà

Φ (t, q, ˙q)

=

1
2

n

X

i,l=1

b

il

(t, q) ˙q

i

˙q

l

, ïðè ïîìîùè êîòîðîé

÷àñòü îáîáù¼ííûõ ñèë âûðàæàåòñÿ ñëåäóþùèì îáðàçîì
Q

∗

i

= −

∂Φ
∂ ˙q

i

.

Äèôôåðåíöèàëüíûå ñâÿçè [1, ñ. 152], [36, ñ. 21]. Ìåõàíè-

÷åñêèå ñâÿçè, óñëîâèÿ f

l

(t, r

i

, V

i

) 6 0

êîòîðûõ ñîäåðæàò

ñêîðîñòè V

i

ìàòåðèàëüíûõ òî÷åê.

Çàêîí

äâèæåíèÿ

öåíòðà

èíåðöèè

[1,

ñ.

73],

[37, ñ. 51]. Óðàâíåíèå mW

C

=

R

âíåøí

, ãäå

m =

N

P

i=1

m

i

ñóììàðíàÿ ìàññà ìåõàíè÷åñêîé ñèñòåìû,

W

C

óñêîðåíèå

öåíòðà

èíåðöèè

ñèñòåìû,

R

âíåøí

ãëàâíûé âåêòîð âíåøíèõ ñèë.

Çàêîí èçìåíåíèÿ èìïóëüñà (êîëè÷åñòâà äâèæåíèÿ)

[1, ñ. 72], [37, ñ. 51]. Óðàâíåíèå ˙Q = R

âíåøí

, ãäå Q

èìïóëüñ (êîëè÷åñòâî äâèæåíèÿ) ñèñòåìû, R

âíåøí

ãëàâíûé âåêòîð âíåøíèõ ñèë.

14

Çàêîí èçìåíåíèÿ êèíåòè÷åñêîãî ìîìåíòà (ìîìåíòà èì-

ïóëüñà,

ìîìåíòà

êîëè÷åñòâà

äâèæåíèÿ)

[1, ñ. 75], [37, ñ. 53]. Óðàâíåíèå

˙

K

O

= M

âíåøí

O

− m [V

O

, V

C

]

,

ãäå K

O

ìîìåíò èìïóëüñà ñèñòåìû (ìîìåíò êîëè-

÷åñòâà äâèæåíèÿ, êèíåòè÷åñêèé ìîìåíò) îòíîñèòåëüíî

òî÷êè O, M

âíåøí

O

ãëàâíûé ìîìåíò îòíîñèòåëüíî òî÷-

êè O âíåøíèõ ñèë, äåéñòâóþùèõ íà ñèñòåìó, m =

N

P

i=1

m

i

ñóììàðíàÿ ìàññà ìåõàíè÷åñêîé ñèñòåìû, V

O

ñêî-

ðîñòü òî÷êè O, V

C

ñêîðîñòü öåíòðà èíåðöèè C ñè-

ñòåìû.

Çàêîí èçìåíåíèÿ êèíåòè÷åñêîé ýíåðãèè â äèôôåðåí-

öèàëüíîé ôîðìå [22, ñ. 170], [37, ñ. 56]. Óðàâíåíèå
dT = δA

, ãäå dT äèôôåðåíöèàë îò êèíåòè÷åñêîé ýíåð-

ãèè ñèñòåìû, δA ýëåìåíòàðíàÿ ðàáîòà ñèë (âíåøíèõ è

âíóòðåííèõ), äåéñòâóþùèõ íà ñèñòåìó.

Çàêîí èçìåíåíèÿ êèíåòè÷åñêîé ýíåðãèè â èíòåãðàëüíîé

ôîðìå [22, ñ. 171], [37, ñ. 56]. Óðàâíåíèå T

2

−T

1

= A

12

,

ãäå T

1

, T

2

êèíåòè÷åñêèå ýíåðãèè ñèñòåìû â íà÷àëå è â

êîíöå ïóòè r

i

(t)

ñèñòåìû, A

12

ðàáîòà ñèë (âíåøíèõ è

âíóòðåííèõ), äåéñòâóþùèõ íà ñèñòåìó, ñîâåðøåííàÿ íà

ïóòè r

i

(t)

.

Çàêîí èçìåíåíèÿ êîëè÷åñòâà äâèæåíèÿ. Ñì. çàêîí èçìå-

íåíèÿ èìïóëüñà.

Çàêîí èçìåíåíèÿ ìîìåíòà èìïóëüñà. Ñì. çàêîí èçìåíåíèÿ

êèíåòè÷åñêîãî ìîìåíòà.

Çàêîí Êåïëåðà, âòîðîé. Ñì. âòîðîé çàêîí Êåïëåðà.
Çàêîí Êåïëåðà, ïåðâûé. Ñì. ïåðâûé çàêîí Êåïëåðà.
Çàêîí Êåïëåðà, òðåòèé. Ñì. òðåòèé çàêîí Êåïëåðà.
Çàêîí Íüþòîíà, âòîðîé. Ñì. âòîðîé çàêîí Íüþòîíà.

15

Çàêîí Íüþòîíà, ïåðâûé. Ñì. ïåðâûé çàêîí Íüþòîíà.
Çàêîí Íüþòîíà, òðåòèé. Ñì. òðåòèé çàêîí Íüþòîíà.
Çàêîí ñîõðàíåíèÿ èìïóëüñà (êîëè÷åñòâà äâèæåíèÿ)

[1, ñ. 72], [37, ñ. 52]. Åñëè ïðîåêöèÿ R

âíåøí

z

íà îñü z

ãëàâíîãî âåêòîðà R

âíåøí

âíåøíèõ ñèë ðàâíà íóëþ, òî

èìåþò ìåñòî çàêîí ñîõðàíåíèÿ ïðîåêöèè èìïóëüñà (êîëè-

÷åñòâà äâèæåíèÿ) íà îñü z è ðàâíîìåðíîñòü äâèæåíèÿ â

íàïðàâëåíèè z öåíòðà èíåðöèè ñèñòåìû.

Çàêîí ñîõðàíåíèÿ êèíåòè÷åñêîãî ìîìåíòà (ìîìåíòà èì-

ïóëüñà,

ìîìåíòà

êîëè÷åñòâà

äâèæåíèÿ)

[1, ñ. 76], [37, ñ. 53]. Åñëè ïðîåêöèÿ M

âíåøí

z

íà îñü z

ãëàâíîãî ìîìåíòà M

âíåøí

O

âíåøíèõ ñèë ðàâíà íóëþ, òî â

ïðåäïîëîæåíèè V

O

= 0

(èëè V

O

||V

C

) èìååò ìåñòî çàêîí

ñîõðàíåíèÿ ïðîåêöèè êèíåòè÷åñêîãî ìîìåíòà (ìîìåíòà

èìïóëüñà, ìîìåíòà êîëè÷åñòâà äâèæåíèÿ) íà îñü z.

Çàêîí ñîõðàíåíèÿ êîëè÷åñòâà äâèæåíèÿ. Ñì. çàêîí ñî-

õðàíåíèÿ èìïóëüñà.

Çàêîí ñîõðàíåíèÿ ìîìåíòà èìïóëüñà. Ñì. çàêîí ñîõðàíå-

íèÿ êèíåòè÷åñêîãî ìîìåíòà.

Çàêîí ñîõðàíåíèÿ ìîìåíòà êîëè÷åñòâà äâèæåíèÿ. Ñì.

çàêîí ñîõðàíåíèÿ êèíåòè÷åñêîãî ìîìåíòà.

Çàêîí ñîõðàíåíèÿ ïîëíîé ìåõàíè÷åñêîé ýíåðãèè

[1, ñ. 78], [37, ñ. 61]. Ïîëíàÿ ìåõàíè÷åñêàÿ ýíåðãèÿ êîí-

ñåðâàòèâíîé ñèñòåìû ñîõðàíÿåòñÿ âî âðåìÿ äâèæåíèÿ.

Çàìêíóòàÿ ñèñòåìà ìàòåðèàëüíûõ òî÷åê [1, ñ. 43],

[37, ñ. 532]. Ìåõàíè÷åñêàÿ ñèñòåìà, ìàòåðèàëüíûå òî÷-

êè êîòîðîé âçàèìîäåéñòâóþò òîëüêî ñ òî÷êàìè, ïðèíàä-

ëåæàùèìè ñèñòåìå.

16

Çíàêîîïðåäåë¼ííûå ôóíêöèè [22, ñ. 535], [37, ñ. 85]. Ïî-

ëîæèòåëüíî îïðåäåë¼ííûå, îòðèöàòåëüíî îïðåäåë¼ííûå

ôóíêöèè.

Çíàêîïîñòîÿííûå ôóíêöèè [22, ñ. 535], [37, ñ. 85]. Ïîëî-

æèòåëüíî ïîñòîÿííûå, îòðèöàòåëüíî ïîñòîÿííûå ôóíê-

öèè.

Çíàêîïåðåìåííûå ôóíêöèè [22, ñ. 535], [37, ñ. 85]. Ôóíê-

öèè, ïðèíèìàþùèå â ëþáîé îêðåñòíîñòè íóëÿ êàê ïîëî-

æèòåëüíûå, òàê è îòðèöàòåëüíûå çíà÷åíèÿ.

Èäåàëüíàÿ ñâÿçü [1, ñ. 159], [36, ñ. 36]. Òàêàÿ ãåîìåòðè÷å-

ñêàÿ ñâÿçü, ÷òî îáîáù¼ííûå ñèëû, ñîîòâåòñòâóþùèå ðåàê-

öèÿì ñâÿçè, ðàâíû íóëþ. Ýêâèâàëåíòíîå îïðåäåëåíèå: íà

ëþáîì âèðòóàëüíîì ïåðåìåùåíèè ñèñòåìû ýëåìåíòàð-

íàÿ ðàáîòà ñèë ðåàêöèè ñâÿçè ðàâíà íóëþ.

Èçîëèðîâàííàÿ ìàòåðèàëüíàÿ òî÷êà [22, ñ. 88],

[37, ñ. 48]. Òî÷êà, íå âçàèìîäåéñòâóþùàÿ ñ äðóãèìè òî÷-

êàìè.

Èçîõðîííûé

äèôôåðåíöèàë

δF (t, q)

[5,

ñ.

14],

[36, ñ. 193]. Äèôôåðåíöèàë ïðè ôèêñèðîâàííîì âðåìåíè

t

: δF (t, q) =

n

X

i=1

∂F
∂q

i

dq

i

.

Èìïóëüñ (êîëè÷åñòâî äâèæåíèÿ) ñèñòåìû ìàòåðèàëü-

íûõ òî÷åê [1, ñ. 56], [37, ñ. 51]. Âû÷èñëÿåòñÿ êàê ãëàâ-

íûé âåêòîð ïî ôîðìóëå

Q =

N

P

i=1

m

i

V

i

=

N

P

i=1

m

i

˙r

i

,

ãäå m

i

, V

i

, r

i

ìàññà, ñêîðîñòü è ðàäèóñ-âåêòîð îòäåëü-

íîé òî÷êè.

Èìïóëüñ (êîëè÷åñòâî äâèæåíèÿ) ìàòåðèàëüíîé òî÷êè

[1, ñ. 55], [37, ñ. 48]. Âû÷èñëÿåòñÿ ïî ôîðìóëå
Q = mV = m˙r

, ãäå m, V, r ìàññà, ñêîðîñòü è ðàäèóñ-

âåêòîð òî÷êè.

17

Èíâîëþöèîííàÿ ñèñòåìà (ñèñòåìà â èíâîëþöèè)

ôóíêöèé [13, ñ. 301], [23, ò. 2, ñ. 547],

[36, ñ. 212]. Ñèñòåìà ôóíêöèé ϕ

i

(t, q, p)

, i = 1, m, ãà-

ìèëüòîíîâûõ ïåðåìåííûõ, äëÿ ñêîáîê Ïóàññîíà êîòîðûõ

âûïîëíÿåòñÿ (ϕ

i

, ϕ

j

) = 0

, i, j = 1, m.

Èíåðöèàëüíàÿ ñèñòåìà îòñ÷¼òà [1, ñ. 44], [37, ñ. 48]. Ñè-

ñòåìà,

â

êîòîðîé

èçîëèðîâàííàÿ

ìàòåðèàëüíàÿ

òî÷êà

äâèæåòñÿ

ñ

ïîñòîÿííîé

ñêîðîñòüþ:

V = ˙r =

const.

Èíòåãðàë ïëîùàäåé [22, ñ. 242], [37, ñ. 64]. Ñîõðàíåíèå

ïðèâåä¼ííîãî ìîìåíòà èìïóëüñà ïðè äâèæåíèè ïîä âîç-

äåéñòâèåì öåíòðàëüíîé ñèëû (ñì. âòîðîé çàêîí

Êåïëåðà).

Èíòåãðàëüíûé èíâàðèàíò [1, ñ. 302], [36, ñ. 171]. Îïðåäå-

ë¼ííûé èíòåãðàë îò ôóíêöèè ãàìèëüòîíîâûõ ïåðåìåí-

íûõ, íå ìåíÿþùèé ñâîåãî çíà÷åíèÿ ïðè ïåðåíîñå îáëà-

ñòè èíòåãðèðîâàíèÿ îïðåäåë¼ííûì îáðàçîì ñîãëàñîâàííî

ñ ôàçîâûì ïîòîêîì ãàìèëüòîíîâîé ñèñòåìû.

Èíòåãðàëüíûé èíâàðèàíò Ïóàíêàðå [1, ñ. 306],

[36, ñ. 173]. Êîíòóðíûé èíòåãðàë

H

C

n

P

i=1

p

i

δq

i

, íå ìåíÿþ-

ùèé ñâîåãî çíà÷åíèÿ ïðè ïåðåíîñå êîíòóðà C â ïðîñòðàí-

ñòâå ñîñòîÿíèé ôàçîâûì ïîòîêîì ëþáîé ãàìèëüòîíî-

âîé ñèñòåìû.

Èíòåãðàëüíûé

èíâàðèàíò

Ïóàíêàðå-Êàðòàíà

[1, ñ. 305], [36, ñ. 172]. Êîíòóðíûé èíòåãðàë

H

C

·

n

P

i=1

p

i

δq

i

− Hδt

¸

: ïî ëþáûì äâóì ñîãëàñîâàííûì êîí-

òóðàì C

0

è C

1

, îõâàòûâàþùèì òðóáêó ïðÿìûõ ïóòåé,

èíòåãðàë ïðèíèìàåò îäíî è òî æå çíà÷åíèå. Òðóáêà ïî-

ðîæäàåòñÿ ôóíêöèåé Ãàìèëüòîíà H, âõîäÿùåé â ïîäûí-

òåãðàëüíîå âûðàæåíèå,

18

Èíòåãðèðóåìàÿ äèôôåðåíöèàëüíàÿ ñâÿçü [1, ñ. 153],

[36, ñ. 21]. Óðàâíåíèå äèôôåðåíöèàëüíîé ñâÿçè
f

l

(t, r

i

, V

i

) = 0

äîïóñêàåò ýêâèâàëåíòíóþ çàìåíó óðàâíå-

íèåì ãåîìåòðè÷åñêîé ñâÿçè. Íàïðèìåð, óðàâíåíèå
V

1

− V

2

= 0

çàìåíÿåòñÿ óðàâíåíèåì r

1

− r

2

− c = 0.

Èíòåðïðåòàöèÿ Ïóàíñî [22, ñ. 198], [30, ñ. 525],

[22, ñ. 198], [37, ñ. 105]. Èíòåðïðåòèðóåò äâèæåíèå òâ¼ð-

äîãî òåëà ñ íåïîäâèæíîé òî÷êîé â ñëó÷àå Ýéëåðà.  íà÷à-

ëå äâèæåíèÿ îáðàçóåòñÿ ïëîñêîñòü, êàñàòåëüíàÿ ê ýëëèï-

ñîèäó èíåðöèè â òî÷êå ïåðåñå÷åíèÿ ýëëèïñîèäà íà÷àëü-

íîé óãëîâîé ñêîðîñòüþ. Â äàëüíåéøåì ïëîñêîñòü çàíè-

ìàåò íåèçìåííîå ïîëîæåíèå, à ýëëèïñîèä èíåðöèè ñ íåïî-

äâèæíûì öåíòðîì êàòàåòñÿ ïî íåé áåç ïðîñêàëüçûâàíèÿ.

Êàíîíè÷åñêèå óðàâíåíèÿ Ãàìèëüòîíà. Òî æå, ÷òî ãàìèëü-

òîíîâà ñèñòåìà.

Êàíîíè÷åñêîå ïðåîáðàçîâàíèå [1, ñ. 323], [36, ñ. 191]. Òà-

êîå íåîñîáåííîå ïðåîáðàçîâàíèå

˜

q = ˜

q (t, q, p)

, ˜p = ˜p(t, q, p)

ãàìèëüòîíîâûõ ïåðåìåííûõ, ÷òî óêàçàííàÿ çàìåíà ïåðå-

ìåííûõ â ëþáîé ãàìèëüòîíîâîé ñèñòåìå ïðèâîäèò ê ãà-

ìèëüòîíîâîé ñèñòåìå.

Êàñàòåëüíîå (òàíãåíöèàëüíîå) óñêîðåíèå [1, ñ. 17],

[37, ñ. 91]. Ïðîåêöèÿ óñêîðåíèÿ ìàòåðèàëüíîé òî÷êè

íà êàñàòåëüíóþ ê òðàåêòîðèè òî÷êè. Ïî âåëè÷èíå ðàâíî
W

τ

= dV/dt, ãäå V âåëè÷èíà ñêîðîñòè òî÷êè.

Êàñàòåëüíîé îðò. Ñì. îðò êàñàòåëüíîé.
Êàñàòåëüíûé

âåêòîð

ê

êîîðäèíàòíîé

ëèíèè

[22, ñ. 28], [37, ñ. 10]. Â âûðàæåíèè ðàäèóñà-âåêòîðà

r

¡

q

0

1

, q

2

, q

0

3

¢

÷åðåç êðèâîëèíåéíûå (îáîáù¼ííûå) êîîðäèíà-

òû èçìåíÿåòñÿ òîëüêî îäíà êîîðäèíàòà, íàïðèìåð, q

2

. Ê

ïîñòðîåííîé êðèâîé (êîîðäèíàòíîé ëèíèè) â òî÷êå q

0

1

, q

0

2

,

q

0

3

ñòðîèòñÿ êàñàòåëüíûé âåêòîð H

i

(q) = ∂r (q)/∂q

i

.

19

Êâàòåðíèîí. Ñì. àëãåáðà êâàòåðíèîíîâ.
ʼíèãà Ñ. ñèñòåìà. Ñì. ñèñòåìà ʼíèãà.
ʼíèãà Ñ. òåîðåìà äëÿ ñèñòåìû ìàòåðèàëüíûõ òî÷åê

[1, ñ. 174], [37, ñ. 57]. Êèíåòè÷åñêàÿ ýíåðãèÿ ñèñòå-
ìû ìàòåðèàëüíûõ òî÷åê ðàâíà T =

1
2

mV

2

C

+ T îòí

, ãäå

m =

N

P

i=1

m

i

ñóììàðíàÿ ìàññà ìåõàíè÷åñêîé ñèñòåìû,

V

C

ñêîðîñòü öåíòðà èíåðöèè C ñèñòåìû, T îòí êè-

íåòè÷åñêàÿ ýíåðãèÿ â ñèñòåìå ʼíèãà.

ʼíèãà Ñ. òåîðåìà äëÿ òâ¼ðäîãî òåëà [1, ñ. 174],

[37, ñ. 58]. Êèíåòè÷åñêàÿ ýíåðãèÿ òâ¼ðäîãî òåëà ðàâíà

T =

1
2

mV

2

C

+

1
2

I

ω

ω

2

, ãäå m =

N

P

i=1

m

i

ñóììàðíàÿ ìàññà

ìåõàíè÷åñêîé ñèñòåìû, V

C

ñêîðîñòü öåíòðà ìàññ C

ñèñòåìû, ω âåëè÷èíà óãëîâîé ñêîðîñòè òåëà, I

ω

ìî-

ìåíò èíåðöèè òåëà îòíîñèòåëüíî ïàðàëëåëüíîé âåêòîðó
ω

îñè, ïðîõîäÿùåé ÷åðåç öåíòð ìàññ òåëà.

Êåïëåðà È. âòîðîé çàêîí. Ñì. âòîðîé çàêîí Êåïëåðà.
Êåïëåðà È. ïåðâûé çàêîí. Ñì. ïåðâûé çàêîí Êåïëåðà.
Êåïëåðà È. òðåòèé çàêîí. Ñì. òðåòèé çàêîí Êåïëåðà.
Êèíåìàòè÷åñêèå óðàâíåíèÿ Ýéëåðà Ë. [1, ñ. 195],

[37, ñ. 82]. Óðàâíåíèÿ

p = ˙

ψ sin θ sin ϕ + ˙θ cos ϕ,

q = ˙

ψ sin θ cos ϕ − ˙θ sin ϕ,

r = ˙

ψ cos θ + ˙

ϕ,

èëè â íîðìàëüíîì âèäå

˙

ψ = (p sin ϕ + q cos ϕ)

1

sin θ

,

˙θ = p cos ϕ − q sin ϕ,

˙

ϕ = r − (p sin ϕ + q cos ϕ) ctg θ,

20

ãäå îáîçíà÷åíî ψ, θ, ϕ óãëû Ýéëåðà, p, q, r ïðîåêöèè

óãëîâîé ñêîðîñòè íà ãëàâíûå îñè èíåðöèè.

Êèíåìàòè÷åñêèå óðàâíåíèÿ â ïàðàìåòðàõ Ðîäðèãà-Ãàìèëüòîíà

[33, ñ. 236], [37, ñ. 90]. Óðàâíåíèÿ









˙λ

0

˙λ

1

˙λ

2

˙λ

3







 =

1
2









0 −p −q −r
p

0

r

−q

q −r

0

p

r

q

−p

0

















λ

0

λ

1

λ

2

λ

3







 ,

ãäå λ

0

, λ

1

, λ

2

, λ

3

ïàðàìåòðû Ðîäðèãà-Ãàìèëüòîíà (êî-

îðäèíàòû êâàòåðíèîíà), p, q, r ïðîåêöèè óãëîâîé ñêî-

ðîñòè íà ãëàâíûå îñè èíåðöèè.

Êèíåìàòè÷åñêèé âèíò [22, ñ. 72], [37, ñ. 40]. Âèíò, ïî-

ñòðîåííûé äëÿ ìíîæåñòâà óãëîâûõ ñêîðîñòåé.

Êèíåòè÷åñêàÿ ýíåðãèÿ ñèñòåìû ìàòåðèàëüíûõ òî÷åê

[1, ñ. 56], [37, ñ. 55]. Âû÷èñëÿåòñÿ ïî ôîðìóëå

T =

1
2

N

X

i=1

m

i

V

2

i

, ãäå m

i

, V

i

ìàññà è ñêîðîñòü îòäåëü-

íîé òî÷êè.

Êèíåòè÷åñêàÿ ýíåðãèÿ òâ¼ðäîãî òåëà ñ íåïîäâèæíîé

òî÷êîé [1, ñ. 190], [37, ñ. 97]. Âû÷èñëÿåòñÿ ïî ôîð-

ìóëå T =

1
2

3

X

k=1

I

k

ω

2

k

−

X

k<l

I

kl

ω

k

ω

l

, ãäå I

k

, I

kl

ýëåìåíòû

òåíçîðà èíåðöèè äëÿ êîíêðåòíîãî îðòîíîðìèðîâàííîãî

áàçèñà, ω

k

êîýôôèöèåíòû ðàçëîæåíèÿ óãëîâîé ñêîðî-

ñòè ïî ýòîìó áàçèñó. Åñëè áàçèñ îïðåäåëÿåò ãëàâíûå îñè
èíåðöèè, ôîðìóëà óïðîùàåòñÿ: T =

1
2

¡

Ap

2

+ Bq

2

+ Cr

2

¢

,

ãäå A, B, C ìîìåíòû èíåðöèè òåëà îòíîñèòåëüíî ãëàâ-

íûõ îñåé èíåðöèè, p, q, r ïðîåêöèè óãëîâîé ñêîðîñòè

íà ýòè îñè.

21

Êèíåòè÷åñêèé ìîìåíò (ìîìåíò èìïóëüñà, ìîìåíò êî-

ëè÷åñòâà äâèæåíèÿ) ñèñòåìû ìàòåðèàëüíûõ òî÷åê

[1, ñ. 74], [37, ñ. 52]. Âû÷èñëÿåòñÿ ïî ôîðìóëå
K

O

=

N

P

i=1

[

r

i

, m

i

V

i

]

, ãäå m

i

, V

i

ìàññà è ñêîðîñòü ìà-

òåðèàëüíîé òî÷êè íîìåð i, r

i

âåêòîð, ïðîâåä¼ííûé èç

òî÷êè O â òî÷êó íîìåð i. Êèíåòè÷åñêèé ìîìåíò îòêëà-

äûâàåòñÿ èç òî÷êè O.

Êèíåòè÷åñêèé ôîêóñ (ñîïðÿæåííûå êèíåòè÷åñêèå ôî-

êóñû) [4, ñ. 70], [27, ò. 2, ñ. 231], [36, ñ. 156]. Äâå òî÷êè

¡

t

0

, q

0

¢

,

¡

t

f

, q

f

¢

ðàñøèðåííîãî êîîðäèíàòíîãî ïðîñòðàí-

ñòâà

R

n+1

,

ðàñïîëîæåííûå

íà

ðåøåíèè

q (t) = q

¡

t, t

0

, q

0

, ˙q

0

¢

óðàâíåíèé Ëàãðàíæà, íàçûâàþòñÿ

ñîïðÿæ¼ííûìè êèíåòè÷åñêèìè ôîêóñàìè, åñëè ñïðàâåä-

ëèâî ðàâåíñòâî det

°

°

°

°

°

∂q

i

¡

t

f

, t

0

, q

0

, ˙q

0

¢

∂ ˙q

0

k

°

°

°

°

°

= 0.

Êîâàëåâñêîé ñëó÷àé [1, ñ. 199], [37, ñ. 101]. Òåëî ñ íåïî-

äâèæíîé òî÷êîé ñîâåðøàåò äâèæåíèå â îäíîðîäíîì ïîëå

òÿæåñòè Çåìëè. Òåëî îáëàäàåò îñüþ äèíàìè÷åñêîé ñèì-

ìåòðèè, ìîìåíò èíåðöèè îòíîñèòåëüíî êîòîðîé ðàâåí
C

. Äëÿ ìîìåíòîâ èíåðöèè îòíîñèòåëüíî ãëàâíûõ îñåé

èíåðöèè âûïîëíÿåòñÿ A = B = 2C. Öåíòð ìàññ ðàñïî-

ëîæåí â ýêâàòîðèàëüíîé ïëîñêîñòè.

Êîëè÷åñòâî äâèæåíèÿ ñèñòåìû ìàòåðèàëüíûõ òî÷åê.

Òî æå, ÷òî èìïóëüñ ñèñòåìû ìàòåðèàëüíûõ òî÷åê.

Êîëè÷åñòâî äâèæåíèÿ ìàòåðèàëüíîé òî÷êè. Òî æå, ÷òî

èìïóëüñ ìàòåðèàëüíîé òî÷êè.

Êîíå÷íàÿ ñâÿçü. Òî æå, ÷òî ãåîìåòðè÷åñêàÿ ñâÿçü.
Êîíå÷íîìåðíàÿ ìåõàíè÷åñêàÿ ñèñòåìà [36, ñ. 5]. Ñèñòå-

ìà, ñîñòîÿùàÿ èç êîíå÷íîãî ÷èñëà ìàòåðèàëüíûõ òî÷åê

è êîíå÷íîãî ÷èñëà òâ¼ðäûõ òåë. Ýêâèâàëåíòíîå îïðåäå-

22

ëåíèå: ìåõàíè÷åñêàÿ ñèñòåìà ñ êîíå÷íûì ÷èñëîì ñòåïå-

íåé ñâîáîäû.

Êîíñåðâàòèâíàÿ ñèñòåìà [8, ñ. 54], [36, ñ. 52]. Ñèñòåìà

íàçûâàåòñÿ êîíñåðâàòèâíîé ïðè âûïîëíåíèè ñëåäóþùèõ

óñëîâèé: ñèñòåìà ñòàöèîíàðíî çàäàíà; ïîòåíöèàëüíàÿ

ýíåðãèÿ çàâèñèò òîëüêî îò îáîáù¼ííûõ êîîðäèíàò; íåïî-

òåíöèàëüíûå ñèëû îòñóòñòâóþò.

Êîíôèãóðàöèîííîå

ìíîãîîáðàçèå

[22,

ñ.

43],

[36, ñ. 22]. Ðàçðåø¼ííûå ìåõàíè÷åñêèìè ñâÿçÿìè ïî-

ëîæåíèÿ ìåõàíè÷åñêîé ñèñòåìû, çàäàííûå â íåêîòîðîì

ïðîñòðàíñòâå, íàïðèìåð, â ïðÿìîì ïðîèçâåäåíèè äåêàð-

òîâûõ êîîðäèíàò îòäåëüíûõ òî÷åê ñèñòåìû.

Êîíôîðìíàÿ ñèììåòðèÿ [14, ñ. 90], [36, ñ. 151]. Íåîñî-

áåííîå ïðåîáðàçîâàíèå ïåðåìåííûõ t, q ↔ bt, bq, ñâÿçàí-

íîå ñ ôóíêöèåé Ëàãðàíæà L (t, q, ˙q) ñëåäóþùèì îáðàçîì

L

Ã

_

t ,

_

q ,

d

_

q

d

_

t

!

= cL (t, q, ˙q)

dt

d

_

t

,

c =

const (èëè â ñèììåò-

ðè÷íîì âèäå

L

Ã

_

t ,

_

q ,

d

_

q

d

_

t

!

d

_

t = cL

µ

t, q,

dq

dt

¶

dt

).

Êîîðäèíàòíàÿ ëèíèÿ [22, ñ. 28], [37, ñ. 10]. Çàäà¼òñÿ ïà-

ðàìåòðè÷åñêè: â âûðàæåíèè ðàäèóñ-âåêòîðà r

¡

q

0

1

, q

2

, q

0

3

¢

÷åðåç êðèâîëèíåéíûå (îáîáù¼ííûå) êîîðäèíàòû èçìåíÿ-

åòñÿ òîëüêî îäíà êîîðäèíàòà, íàïðèìåð, q

2

.

Êîîðäèíàòíîå ïðîñòðàíñòâî [22, ñ. 43], [36, ñ. 4]. n-ìåðíîå

ïðîñòðàíñòâî ñ êîîðäèíàòàìè q

1

, . . . , q

n

(îáîáù¼ííûå êî-

îðäèíàòû).

Êîðèîëèñà Ãóñòàâà Ãàñïàðà òåîðåìà (òåîðåìà Êîðèîëè-

ñà, òåîðåìà î ñëîæåíèè óñêîðåíèé â ñëîæíîì äâè-

æåíèè) [22, ñ. 75], [37, ñ. 24]. Àáñîëþòíîå óñêîðåíèå
Wàáñ ìàòåðèàëüíîé òî÷êè â ñëîæíîì äâèæåíèè îïðå-

23

äåëÿåòñÿ ôîðìóëîé Wàáñ = Wïåð + Wîòí + Wêîð, ãäå

Wïåð ïåðåíîñíîå óñêîðåíèå, Wîòí îòíîñèòåëüíîå

óñêîðåíèå, Wêîð = 2

£

ωïåð, Vîòí

¤

êîðèîëèñîâî óñêî-

ðåíèå (ωïåð óãëîâàÿ ñêîðîñòü ïîäâèæíîé ñèñòåìû êî-

îðäèíàò, Vîòí îòíîñèòåëüíàÿ ñêîðîñòü òî÷êè).

Êîðèîëèñîâà ñèëà èíåðöèè [1, ñ. 107], [37, ñ. 49]. Âû-

÷èñëÿåòñÿ ïî ôîðìóëå Jêîð = −2m

£

ωïåð, Vîòí

¤

, ãäå

m ìàññà òî÷êè, ωïåð óãëîâàÿ ñêîðîñòü ïîäâèæíîé

ñèñòåìû êîîðäèíàò, Vîòí îòíîñèòåëüíàÿ ñêîðîñòü

òî÷êè.

Êîðèîëèñîâî óñêîðåíèå [1, ñ. 34], [37, ñ. 24]. Âû÷èñëÿåòñÿ

ïî

ôîðìóëå

Wêîð

=

2

£

ωïåð, Vîòí

¤

,

ãäå

ωïåð óãëîâàÿ ñêîðîñòü ïîäâèæíîé ñèñòåìû êîîðäè-

íàò, Vîòí îòíîñèòåëüíàÿ ñêîðîñòü òî÷êè.

Êîýôôèöèåíò Ëàìå [22, ñ. 28], [37, ñ. 11]. Âåëè÷èíà êàñà-

òåëüíîãî

âåêòîðà

ê

êîîðäèíàòíîé

êðèâîé:

H

i

(q) = |H

i

(q)| =

¯

¯

¯∂r (q)/∂q

i

¯

¯

¯

.

Êðèâèçíà. Ñì. âåêòîð êðèâèçíû.
Êðèâîëèíåéíûå (îáîáù¼ííûå êîîðäèíàòû) ìàòåðèàëü-

íîé òî÷êè [22, ñ. 27], [37, ñ. 10]. Êîîðäèíàòû q

1

, q

2

, q

3

,

çàäàþùèå ðàäèóñ-âåêòîð r (q

1

, q

2

, q

3

)

òî÷êè è óäîâëåòâî-

ðÿþùèå óñëîâèÿì: 1. ÷èñëà q

1

, q

2

, q

3

íàõîäÿòñÿ âî âçàèìíî

îäíîçíà÷íîì ñîîòâåòñòâèè ñ ëþáûì ïîëîæåíèåì òî÷êè â

ñèñòåìå îòñ÷¼òà; 2. êàñàòåëüíûå âåêòîðû ê êîîðäèíàò-

íûì ëèíèÿì â êàæäîé òî÷êå ñèñòåìû îòñ÷¼òà ëèíåéíî

íåçàâèñèìû.

Êðèòåðèé Ìèõàéëîâà [1, ñ. 229], [36, ñ. 117]. Ìíîãî÷ëåí

ñòåïåíè n óñòîé÷èâ òîãäà è òîëüêî òîãäà, êîãäà äëÿ ïðè-

ðàùåíèÿ àðãóìåíòà θ ó ãîäîãðàôà Ìèõàéëîâà âûïîëíÿåò-
ñÿ

∞

∆

ω=0

θ = n

π

2

.

24

Êðèòåðèé ðàâíîâåñèÿ ñòàöèîíàðíî çàäàííîé ñèñòåìû

(ïðèíöèï

âîçìîæíûõ

ïåðåìåùåíèé)

[1, ñ. 216], [37, ñ. 80]. Ïîëîæåíèå r

0

i

, i = 1, N,

(q

0

k

, k = 1, n) ñòàöèîíàðíî çàäàííîé ñèñòåìû ñ èäåàëü-

íûìè ñâÿçÿìè ÿâëÿåòñÿ ïîëîæåíèåì ðàâíîâåñèÿ òîãäà è

òîëüêî òîãäà, êîãäà íà ëþáîì âîçìîæíîì ïåðåìåùåíèè
dr

i

èç ýòîãî ïîëîæåíèÿ äëÿ ýëåìåíòàðíîé ðàáîòû àêòèâ-

íûõ

ñèë

F

i

âûïîëíÿåòñÿ

δA =

N

P

i=1

(F

i

, dr

i

) =

n

P

k=1

Q

k

¡

t, q

0

, 0

¢

dq

k

=0

. Ýêâèâàëåíòíàÿ

ôîðìóëèðîâêà: ïîëîæåíèå r

0

i

, i = 1, N, (q

0

k

, k = 1, n) ñòà-

öèîíàðíî çàäàííîé ñèñòåìû ñ èäåàëüíûìè ñâÿçÿìè ÿâëÿ-

åòñÿ ïîëîæåíèåì ðàâíîâåñèÿ òîãäà è òîëüêî òîãäà, êîãäà

äëÿ îáîáù¼ííûõ ñèë Q

k

(t, q, ˙q)

òîæäåñòâåííî ïî âðåìå-

íè t âûïîëíÿåòñÿ Q

k

¡

t, q

0

, 0

¢

= 0

.

Êðèòåðèé Ðàóñà-Ãóðâèöà [8, ñ. 196], [36, ñ. 119]. Ìíî-

ãî÷ëåí óñòîé÷èâ òîãäà è òîëüêî òîãäà, êîãäà âñå ãëàâ-

íûå öåíòðàëüíûå ìèíîðû îïðåäåëèòåëÿ Ãóðâèöà ïîëî-

æèòåëüíû.

Êðóãîâàÿ (óãëîâàÿ, öèêëè÷åñêàÿ) ÷àñòîòà ãàðìîíè÷å-

ñêîãî

êîëåáàíèÿ

[6,

÷.

1,

ñ.

59],

[23, ò. 1, ñ. 888] [32, ñ. 848]. Âåëè÷èíà ω â ãàðìîíè÷å-

ñêîì êîëåáàíèè x = A sin (ωt + α). Èíîãäà âåëè÷èíó ω íà-

çûâàþò

ïðîñòî

÷àñòîòîé

[8,

ñ.

202],

[13, ñ. 177].

Ëàãðàíæà ñëó÷àé äâèæåíèÿ òâåðäîãî òåëà [1, ñ. 195],

[37, ñ. 107]. Òåëî ñ íåïîäâèæíîé òî÷êîé ñîâåðøàåò äâè-

æåíèå â îäíîðîäíîì ïîëå òÿæåñòè Çåìëè. Òåëî îáëàäàåò

äèíàìè÷åñêîé ñèììåòðèåé. Öåíòð ìàññ ðàñïîëîæåí íà

îñè äèíàìè÷åñêîé ñèììåòðèè.

Ëàãðàíæåâà

ñèñòåìà

(óðàâíåíèÿ

Ëàãðàíæà)

[1, ñ. 132], [36, ñ. 36]. Ñèñòåìà îáûêíîâåííûõ äèôôå-

25

ðåíöèàëüíûõ óðàâíåíèé âû÷èñëÿåòñÿ èëè, èñõîäÿ èç êè-

íåòè÷åñêîé ýíåðãèè T (t, q, ˙q) è îáîáùåííûõ ñèë Q

k

(t, q, ˙q)

:

d

dt

∂T

∂ ˙q

k

−

∂T

∂q

k

= Q

k

,

èëè, èñõîäÿ èç ëàãðàíæèàíà L (t, q, ˙q):

d

dt

∂L

∂ ˙q

k

−

∂L

∂q

k

= 0

.

Âîçìîæåí ïðîìåæóòî÷íûé âèä:

d

dt

∂T

∂ ˙q

k

−

∂T

∂q

k

= −

∂Π
∂q

k

−

∂Φ

∂ ˙q

k

+ e

Q

k

,

ãäå Π ïîòåíöèàëüíàÿ ýíåðãèÿ, Φ äèññèïàòèâíàÿ

ôóíêöèÿ Ðåëåÿ, e

Q

k

íåïîòåíöèàëüíûå è íåäèññèïàòèâ-

íûå ñèëû.

Ëàãðàíæåâû ïåðåìåííûå (ïåðåìåííûå Ëàãðàíæà)

[36, ñ. 136]. Ñîâîêóïíîñòü ïåðåìåííûõ: âðåìÿ t,

îáîáùåííûå êîîðäèíàòû q

i

, îáîáùåííûå ñêîðîñòè ˙q

i

.

Ëàãðàíæèàí

(ôóíêöèÿ

Ëàãðàíæà)

[1,

ñ.

137],

[36, ñ. 37]. Ôóíêöèÿ L (t, q, ˙q) ëàãðàíæåâûõ ïåðåìåííûõ,

ïðè ïîìîùè êîòîðîé âû÷èñëÿþòñÿ óðàâíåíèÿ Ëàãðàíæà.

Ëàãðàíæèàí ñâÿçàí ñ ãàìèëüòîíèàíîì ñëåäóþùèì îá-

ðàçîì:

L =

n

P

i=1

p

i

˙q

i

− H

.

Ëîêàëüíûé

áàçèñ

êðèâîëèíåéíûõ

êîîðäèíàò

[37, ñ. 11]. Êàñàòåëüíûå âåêòîðû H

1

(q)

, H

2

(q)

,

H

3

(q)

ê êîîðäèíàòíûì êðèâûì, êîòîðûå ïî îïðåäåëå-

íèþ êðèâîëèíåéíûõ êîîðäèíàò â êàæäîé òî÷êå ñèñòåìû

îòñ÷¼òà ëèíåéíî íåçàâèñèìû.

Ìàëûå

êîëåáàíèÿ

(ëèíåéíûå

êîëåáàíèÿ)

[22, ñ. 518], [36, ñ. 97]. Äâèæåíèå êîíñåðâàòèâíîé ñè-

ñòåìû â îêðåñòíîñòè óñòîé÷èâîãî ïîëîæåíèÿ ðàâíîâå-

ñèÿ. Äâèæåíèå îïðåäåëÿåòñÿ ëèíåéíûìè óðàâíåíèÿìè Ëà-

ãðàíæà è ÿâëÿåòñÿ ëèíåéíîé êîìáèíàöèåé ãëàâíûõ êî-

ëåáàíèé.

26

Ìàññà [22, ñ. 89], [37, ñ. 6]. Ïîëîæèòåëüíîå ÷èñëî m, ïðèïè-

ñûâàåìîå ìàòåðèàëüíîé òî÷êå.

Ìàòåðèàëüíàÿ òî÷êà [22, ñ. 87], [37, ñ. 6]. Òî÷êà, êîòîðîé

ïîñòàâëåíî â ñîîòâåòñòâèå ïîëîæèòåëüíîå ÷èñëî ìàññà
m

.

Ìàòðèöà íàïðàâëÿþùèõ êîñèíóñîâ (ìàòðèöà ïîâîðîòà)

[9, ñ. 112], [19, ñ. 42], [37, ñ. 79]. Ìàòðèöà A = ka

kl

k

çàäà¼ò ðàçëîæåíèå êàæäîãî âåêòîðà îðòîíîðìèðîâàííîãî

áàçèñà e

1

, e

2

, e

3

, ñâÿçàííîãî ñ òâ¼ðäûì òåëîì, ïî áàçèñó

i

1

, i

2

, i

3

, ñâÿçàííîìó ñ ñèñòåìîé îòñ÷¼òà: e

k

=

N

P

l=1

a

kl

i

l

.

Ìàòðèöà ïîâîðîòà. Ñì. ìàòðèöà íàïðàâëÿþùèõ êîñèíóñîâ.
Ìãíîâåííîå

(÷èñòîå)

âðàùåíèå

[22,

ñ.

58],

[37, ñ. 32]. Ñîñòîÿíèå òâåðäîãî òåëà, ïðè êîòîðîì ñêî-

ðîñòè V

i

òî÷åê r

i

òåëà îïðåäåëÿþòñÿ óãëîâîé ñêîðîñòüþ

ω

òåëà ñëåäóþùèì îáðàçîì: V

i

= [ω,

r

i

]

.

Ìåõàíè÷åñêàÿ ñèñòåìà [22, ñ. 20], [37, ñ. 3]. Ñèñòåìà, ñî-

ñòîÿùàÿ èç ìàòåðèàëüíûõ òî÷åê.

Ìåõàíè÷åñêèå ñâÿçè [1, ñ. 149], [36, ñ. 21]. Îãðàíè÷åíèÿ

f

l

(t, r

i

, V

i

) 6 0

, íàëîæåííûå íà ñîñòîÿíèÿ ìåõàíè÷åñêîé

ñèñòåìû, ñïðàâåäëèâûå äëÿ íà÷àëüíûõ ñîñòîÿíèé è âî

âðåìÿ äâèæåíèÿ.

Ìåùåðñêîãî óðàâíåíèå [1, ñ. 123], [37, ñ. 74]. Óðàâíåíèå

ïîñòóïàòåëüíîãî äâèæåíèÿ òåëà ïåðåìåííîãî ñîñòàâà:

m

dV

dt

= Râíåøí −

n

X

i=1

dmóõ

i

dt

uóõ

i

+

r

X

k=1

dmïð

k

dt

uïð

k

,

ãäå m,

móõ

i

, mïð

k

ìàññà òåëà, óõîäÿùèå è ïðèõîäÿùèå ìàññû,

V

ñêîðîñòü òåëà, Râíåøí ãëàâíûé âåêòîð äåéñòâóþ-

ùèõ íà òåëî âíåøíèõ ñèë, uóõ

i

,

uïð

k

ñêîðîñòè óõîäÿ-

ùèõ è ïðèõîäÿùèõ ìàññ â ïîäâèæíîé ñèñòåìå, ñâÿçàííîé

ñ òåëîì.

27

Ìíèìàÿ

÷àñòîòíàÿ

õàðàêòåðèñòèêà

[12,

ñ.

45],

[36,

ñ.

131].

Çàâèñèìîñòü

ìíèìîé

÷àñòè

S

jk

(Ω) = ImW

jk

(iΩ)

àìïëèòóäíî-ôàçîâîé õàðàêòåðè-

ñòèêè W

jk

(iΩ) = P

jk

(Ω) + iS

jk

(Ω)

îò ïåðåìåííîé Ω.

Ìîìåíò âåêòîðà [1, ñ. 352], [30, ñ. 14], [37, ñ. 37]. Âû÷èñ-

ëÿåòñÿ ïî ôîðìóëå M

O

(a) = [r, a]

, ãäå r ïðîâîäèòñÿ èç

òî÷êè O ê íà÷àëüíîé òî÷êå âåêòîðà a.

Ìîìåíò èìïóëüñà ñèñòåìû ìàòåðèàëüíûõ òî÷åê. Ñì. êè-

íåòè÷åñêèé ìîìåíò.

Ìîìåíò èíåðöèè òâ¼ðäîãî òåëà îòíîñèòåëüíî îñè

[1, ñ. 117], [37, ñ. 92]. Âû÷èñëÿåòñÿ ïî ôîðìóëå I

e

=

P

i

m

i

h

2

i

, ãäå m

i

ìàññà ÷àñòèöû òåëà, h

i

ðàññòîÿíèå

÷àñòèöû äî îñè.

Ìîìåíò êîëè÷åñòâà äâèæåíèÿ ñèñòåìû ìàòåðèàëüíûõ

òî÷åê. Ñì. êèíåòè÷åñêèé ìîìåíò.

Ìîìåíò ñèëû. Ñì. ìîìåíò âåêòîðà.
Ìîìåíòû èíåðöèè òâ¼ðäîãî òåëà öåíòðîáåæíûå

[1, ñ. 180], [37, ñ. 93]. Äëÿ ôèêñèðîâàííîé îðòîíîðìèðî-

âàííîé ñèñòåìû êîîðäèíàò âû÷èñëÿþòñÿ ÷åðåç êîîðäèíà-

òû x

i1

, x

i2

, x

i3

÷àñòèöû òåëà ïî ôîðìóëàì

I

12

= I

21

=

P

i

m

i

x

i1

x

i2

, I

13

= I

31

=

P

i

m

i

x

i1

x

i3

,

I

23

= I

32

=

P

i

m

i

x

i2

x

i3

, ãäå m

i

ìàññà ÷àñòèöû òåëà.

Ìîùíîñòü ñèëû [22, ñ. 285], [37, ñ. 56]. Âû÷èñëÿåòñÿ ïî

ôîðìóëå N = (F, V), ãäå V ñêîðîñòü òî÷êè ïðèëîæå-

íèÿ ñèëû F.

Íàòóðàëüíàÿ ñèñòåìà [22, ñ. 291], [37, ñ. 37]. Ñèñòåìà,

äèíàìèêà êîòîðîé îïèñûâàåòñÿ óðàâíåíèÿìè Ëàãðàíæà

ñ ôóíêöèåé Ëàãðàíæà L = T − V (T êèíåòè÷åñêàÿ

ýíåðãèÿ, V îáîáù¼ííûé ïîòåíöèàë).

28

Íà÷àëî Ãàìèëüòîíà. Òî æå, ÷òî âàðèàöèîííûé ïðèíöèï Ãà-

ìèëüòîíà.

Íà÷àëüíàÿ

ôàçà

ãàðìîíè÷åñêîãî

êîëåáàíèÿ

[32, ñ. 110], [23, ò. 1, ñ. 888]. Âåëè÷èíà α â ãàðìîíè÷å-

ñêîì êîëåáàíèè x = A sin (ωt + α).

Íåèçîëèðîâàííàÿ ìàòåðèàëüíàÿ òî÷êà [22, ñ. 88],

[37, ñ. 48]. Òî÷êà, âçàèìîäåéñòâóþùàÿ ñ äðóãèìè òî÷-

êàìè.

Íåèíåðöèàëüíàÿ

ñèñòåìà

îòñ÷¼òà

[1,

ñ.

106],

[37, ñ. 48]. Ñèñòåìà, â êîòîðîé èçîëèðîâàííàÿ ìàòåðè-

àëüíàÿ òî÷êà äâèæåòñÿ ñ ïåðåìåííîé ñêîðîñòüþ: V (t) 6=

const.

Íåèíòåãðèðóåìàÿ

äèôôåðåíöèàëüíàÿ

ñâÿçü

[1, ñ. 153], [36, ñ. 21]. Äèôôåðåíöèàëüíàÿ ñâÿçü, êîòîðàÿ

íå ÿâëÿåòñÿ èíòåãðèðóåìîé.

Íåíàòóðàëüíàÿ ñèñòåìà Íå ÿâëÿåòñÿ íàòóðàëüíîé ñèñòå-

ìîé.

Íåîáõîäèìîå

óñëîâèå

óñòîé÷èâîñòè

ìíîãî÷ëåíà

[1, ñ. 226], [37, ñ. 118]. Åñëè ìíîãî÷ëåí

a

0

λ

m

+ a

1

λ

m−1

+ · · · + a

m−1

λ + a

m

(a

0

> 0)

óñòîé÷èâ, òî äëÿ åãî êîýôôèöèåíòîâ âûïîëíÿåòñÿ:
a

1

> 0

, . . . , a

m

> 0

.

Íåïîòåíöèàëüíûå ñèëû. Ñèëû, íå ÿâëÿþùèåñÿ ïîòåíöè-

àëüíûìè.

Íåñòàöèîíàðíî çàäàííàÿ ñèñòåìà [36, ñ. 26]. Ïîëîæåíèÿ

r

i

(t, q)

òî÷åê ìåõàíè÷åñêîé ñèñòåìû åñòü âåêòîð-ôóíêöèè

íå òîëüêî îáîáù¼ííûõ êîîðäèíàò, íî è ÿâíî âðåìåíè t.

Íåñòàöèîíàðíûå ñâÿçè (ðåîíîìíûå ñâÿçè) [1, ñ. 153],

[36, ñ. 21]. Îãðàíè÷åíèÿ f

l

(t,

r

i

,

V

i

) 6 0

íà äâèæåíèå

ìåõàíè÷åñêîé ñèñòåìû, ñîäåðæàùèå ÿâíî âðåìÿ t.

29

Íåòåðîâñêàÿ ñèììåòðèÿ. Ñì. âàðèàöèîííàÿ ñèììåòðèÿ.
Íåóäåðæèâàþùàÿ ñâÿçü [1, ñ. 151], [36, ñ. 21]. Îãðàíè-

÷åíèå f (t, r

i

,

V

i

) 6 0

òèïà íåðàâåíñòâà, íàëîæåííîå íà

ñîñòîÿíèÿ òî÷åê ìåõàíè÷åñêîé ñèñòåìû.

Íåóñòîé÷èâîñòü ïî Ëÿïóíîâó [1, ñ. 223], [36, ñ. 84]. Ðåøå-

íèå

x

=

0

ñèñòåìû â íîðìàëüíîì âèäå

˙x = ϕ (x)

, x ∈ R

n

,

íåóñòîé÷èâî ïî Ëÿïóíîâó, åñëè äëÿ

îáùåãî ðåøåíèÿ x (t − t

0

, x

0

)

âûïîëíÿåòñÿ:

∃ε > 0, ∀δ > 0, ∃|x

0

| < δ, ∃t

1

> t

0

, |x (t

1

− t

0

, x

0

) | > ε

.

Íîðìà êâàòåðíèîíà [13, ñ. 34], [33, ñ. 39], [37, ñ. 84]. Âû-

÷èñëÿåòñÿ ïî ôîðìóëå

Λ ◦ ˜

Λ = ˜

Λ ◦ Λ = λ

2

0

+ λ

2

1

+ λ

2

2

+ λ

2

3

,

ãäå ˜Λ êâàòåðíèîí, ñîïðÿæ¼ííûé êâàòåðíèîíó Λ, λ

k

ïàðàìåòðû Ðîäðèãà-Ãàìèëüòîíà.

Íîðìàëè îðò. Ñì. îðò íîðìàëè.
Íîðìàëüíîå óñêîðåíèå W

n

[1, ñ. 17], [37, ñ. 9]. Ïðîåêöèÿ

óñêîðåíèÿ íà íàïðàâëåíèå âåêòîðà êðèâèçíû K (íàïðàâ-

ëåíèå îðòà íîðìàëè n).

Íîðìàëüíûå êîîðäèíàòû. Òî æå, ÷òî ãëàâíûå êîîðäèíàòû.
Íîðìèðîâàííûé êâàòåðíèîí [33, ñ. 39], [37, ñ. 85]. Êâà-

òåðíèîí, íîðìà êîòîðîãî ðàâíà åäèíèöå.

Íüþòîíà âòîðîé çàêîí. Ñì. âòîðîé çàêîí Íüþòîíà.
Íüþòîíà ïåðâûé çàêîí. Ñì. ïåðâûé çàêîí Íüþòîíà.
Íüþòîíà òðåòèé çàêîí. Ñì. òðåòèé çàêîí Íüþòîíà.
Îáëàñòü ïðèòÿæåíèÿ [28, ñ. 18], [36, ñ. 109]. Òàêàÿ

∆

-îêðåñòíîñòü ðåøåíèÿ x ≡ 0 ñèñòåìû â íîðìàëüíîì âè-

äå ˙x = ϕ (x) , x ∈ R

n

, ÷òî äëÿ îáùåãî ðåøåíèÿ x (t − t

0

, x

0

)

âûïîëíÿåòñÿ:

{|x

0

| < ∆} ⇒ { lim

t→∞

x (t − t

0

, x

0

) = 0}

.

30

Îáîáù¼ííàÿ ñèëà [1, ñ. 134], [36, ñ. 15]. Ïîëîæåíèå ëþ-

áîé òî÷êè ìåõàíè÷åñêîé ñèñòåìû âûðàæåíî êàê ôóíê-

öèÿ r

i

(t, q)

âðåìåíè è îáîáù¼ííûõ êîîðäèíàò. Îáîáù¼í-

íàÿ ñèëà, ñîîòâåòñòâóþùàÿ êîîðäèíàòå q

k

, îïðåäåëÿåòñÿ

âûðàæåíèåì Q

k

=

X

i

µ

F

i

,

∂

r

i

∂q

k

¶

, ãäå F

i

ñèëà, ïðèëî-

æåííàÿ ê òî÷êå r

i

. Ýêâèâàëåíòíîå îïðåäåëåíèå: êîýôôè-

öèåíò ïðè δq

k

â ýëåìåíòàðíîé ðàáîòå

δA =

P

i

(

F

i

, δ

r

i

) =

P

k

Q

k

δq

k

íà âèðòóàëüíûõ ïåðåìåùåíèÿõ ñèñòåìû.

Îáîáù¼ííî êîíñåðâàòèâíàÿ ñèñòåìà [1, ñ. 272],

[36, ñ. 140]. Ãàìèëüòîíîâà ñèñòåìà, ó êîòîðîé ôóíê-

öèÿ Ãàìèëüòîíà H (q, p) ÿâíî íå çàâèñèò îò âðåìåíè t.

Îáîáù¼ííî êîíñåðâàòèâíàÿ ñèñòåìà ïîðîæäàåò ïåðâûé

èíòåãðàë H (q, p) = c ñîîòâåòñòâóþùåé ãàìèëüòîíîâîé

ñèñòåìû.

Îáîáù¼ííûå èìïóëüñû p

i

[1, ñ. 267], [36, ñ. 135]. Îïðåäå-

ëÿþòñÿ ÷åðåç ôóíêöèþ Ëàãðàíæà:

p

i

=

∂L (t, q, ˙q)

∂ ˙q

i

.

Îáîáù¼ííûå êîîðäèíàòû q

i

[1, ñ. 156], [36, ñ. 19]. Êîîðäè-

íàòû q

1

, . . . , q

n

, îïðåäåëÿþùèå äîïóñòèìûå íàëîæåííûìè

íà ñèñòåìó ñâÿçÿìè ïîëîæåíèÿ ìåõàíè÷åñêîé ñèñòåìû è

óäîâëåòâîðÿþùèå ñëåäóþùèì òðåáîâàíèÿì:

1) ÷èñëà q

1

, . . . , q

n

â ìîìåíò âðåìåíè t íàõîäÿòñÿ âî âçà-

èìíî îäíîçíà÷íîì ñîîòâåòñòâèè ñ ïîëîæåíèÿìè, äîïóñòè-

ìûìè ñâÿçÿìè;

2) êîîðäèíàòû q

1

, . . . , q

n

íåçàâèñèìû ìîæíî èçìåíÿòü

îäíó èç íèõ ïðè ôèêñèðîâàííûõ äðóãèõ;

3) ïðè èçìåíåíèè îäíîé êîîðäèíàòû q

j

â ïðîñòðàíñòâå, â

êîòîðîì çàäà¼òñÿ ïðîèçâîëüíîå ïîëîæåíèå ñèñòåìû, âû-

÷åð÷èâàåòñÿ êîîðäèíàòíàÿ ëèíèÿ è êàñàòåëüíûé âåêòîð

H

j

ê íåé â òî÷êå q

0

, âåêòîðû H

1

, . . . ,

H

n

äîëæíû áûòü

ëèíåéíî íåçàâèñèìû.

31

Îáîáù¼ííûå ñêîðîñòè ˙q

i

[1, ñ. 156], [36, ñ. 25]. Ïðîèçâîä-

íûå ïî âðåìåíè t îò îáîáù¼ííûõ êîîðäèíàò q

i

.

Îáîáù¼ííûé ïîòåíöèàë [1, ñ. 161], [36, ñ. 55]. Ôóíêöèÿ

V (t, q, ˙q)

, ñâÿçàííàÿ ñ îáîáù¼ííûìè ñèëàìè Q

k

ñëåäóþ-

ùèì âûðàæåíèåì: Q

k

=

d

dt

∂V

∂ ˙q

k

−

∂V

∂q

k

.

Îáðàòíàÿ

çàäà÷à

ëàãðàíæåâà

ôîðìàëèçìà

[36, ñ. 57]. Âîçìîæíî ëè êîíêðåòíóþ ñèñòåìó îáûêíî-

âåííûõ äèôôåðåíöèàëüíûõ óðàâíåíèé âòîðîãî ïîðÿäêà

ýêâèâàëåíòíî (íå ìåíÿÿ ìíîæåñòâà ðåøåíèé) çàìåíèòü

óðàâíåíèÿìè Ëàãðàíæà? Ïðè ïîëîæèòåëüíîì îòâåòå ñäå-

ëàòü ýòó çàìåíó.

Îáðàòíûå òåîðåìû òåîðèè èíòåãðàëüíûõ èíâàðèàíòîâ

[1, ñ. 308], [36, ñ. 173]. Òåîðåìû óòâåðæäàþò: åñëè äëÿ

ñèñòåìû îáûêíîâåííûõ äèôôåðåíöèàëüíûõ óðàâíåíèé â

íîðìàëüíîì âèäå èìååò ìåñòî èíâàðèàíòíîñòü èíòåãðà-

ëà Ïóàíêàðå (èëè Ïóàíêàðå-Êàðòàíà), òî ñèñòåìà óðàâ-

íåíèé ãàìèëüòîíîâà.

Îáùåå óðàâíåíèå äèíàìèêè [8, ñ. 23], [13, ñ. 75]. Äëÿ ìå-

õàíè÷åñêèõ ñèñòåì ñ èäåàëüíûìè ñâÿçÿìè ñïðàâåäëèâî

äèíàìè÷åñêîå óðàâíåíèå

N

P

i=1

(m

i

W

i

−

F

i

, δ

r

i

) = 0

,

ãäå m

i

ìàññà îòäåëüíîé òî÷êè, W

i

óñêîðåíèå òî÷êè,

F

i

àêòèâíàÿ ñèëà, ïðèëîæåííàÿ ê òî÷êå, δr

i

ïðîèç-

âîëüíîå âèðòóàëüíîå ïåðåìåùåíèå èç ýòîé òî÷êè.

Îáùåå óðàâíåíèå ñòàòèêè (ïðèíöèï âèðòóàëüíûõ ïå-

ðåìåùåíèé) [1, ñ. 214], [22, ñ. 115]. Ìåõàíè÷åñêàÿ

ñèñòåìà ñ èäåàëüíûìè ñâÿçÿìè íàõîäèòñÿ â ïîëîæåíèè

ðàâíîâåñèÿ r

0

i

òîãäà è òîëüêî òîãäà, êîãäà â ïîëîæåíèè r

0

i

ñïðàâåäëèâî óðàâíåíèå

N

P

i=1

(

F

i

, δ

r

i

) = 0

, ãäå F

i

àêòèâ-

32

íûå ñèëû, ïðèëîæåííûå ê òî÷êàì r

0

i

, δr

i

ïðîèçâîëüíîå

âèðòóàëüíîå ïåðåìåùåíèå èç r

0

i

.

Îäíîìåðíîå òåëî [36, ñ. 7]. Òâ¼ðäîå òåëî, êîòîðîìó ñîîò-

âåòñòâóåò îäíîìåðíàÿ âûïóêëàÿ îáîëî÷êà.

Îäíîïàðàìåòðè÷åñêàÿ

ãðóïïà

ïðåîáðàçîâàíèé

[13, ñ. 218], [36, ñ. 152]. Îáùåå ðåøåíèå

_

x =

_

x (x, t)

ñèñòåìû îáûêíîâåííûõ äèôôåðåíöèàëüíûõ àâòîíîìíûõ
(ñòàöèîíàðíûõ) óðàâíåíèé â íîðìàëüíîì âèäå ˙

_

x = ϕ

¡

_

x

¢

,

_

x ∈ R

n

, ïðè íà÷àëüíûõ óñëîâèÿõ

_

x (0) = x

. Âîçìîæåí

ïåðåõîä ê äðóãîìó ïàðàìåòðó t = f (τ).

Îêîëüíûé ïóòü [1, ñ. 288], [36, ñ. 144]. Ãðàôèê äâèæåíèÿ

â îäíîì èç ïðîñòðàíñòâ (êîîðäèíàòíîì, ðàñøèðåííîì êî-

îðäèíàòíîì è ò. ä.), íå ÿâëÿþùèéñÿ ðåøåíèåì óðàâíåíèé

äèíàìèêè (óðàâíåíèé Ëàãðàíæà, óðàâíåíèé Ãàìèëüòîíà

è ò. ä.).

Îïðåäåë¼ííî-äèññèïàòèâíàÿ ñèñòåìà. Ñì. äèññèïàòèâíàÿ

ñèñòåìà.

Îïðåäåë¼ííî-îòðèöàòåëüíàÿ (îòðèöàòåëüíî îïðåäåë¼í-

íàÿ)

ôóíêöèÿ

[22,

ñ.

535],

[28,

ñ.

10],

[36, ñ. 85]. Äëÿ ôóíêöèè â íåêîòîðîé îáëàñòè, ñîäåð-
æàùåé òî÷êó x = 0, âûïîëíÿåòñÿ V (x)

½

= 0, x = 0,
< 0, x 6= 0.

Îïðåäåë¼ííî-ïîëîæèòåëüíàÿ (ïîëîæèòåëüíî îïðåäåë¼í-

íàÿ)

ôóíêöèÿ

[22,

ñ.

535],

[28,

ñ.

10],

[37, ñ. 85]. Äëÿ ôóíêöèè â íåêîòîðîé îáëàñòè, ñîäåð-
æàùåé òî÷êó x = 0, âûïîëíÿåòñÿ V (x)

½

= 0, x = 0,
> 0, x 6= 0.

33

Îïðåäåëèòåëü Ãóðâèöà [1, ñ. 227], [36, ñ. 119]. Ñòðîèòñÿ

ïî êîýôôèöèåíòàì ìíîãî÷ëåíà

a

0

λ

m

+ a

1

λ

m−1

+ · · · + a

m−1

λ + a

m

:

∆

m

=

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

a

1

a

3

a

5

a

7

. . . . . . . . .

0

a

0

a

2

a

4

a

6

. . . . . . . . .

.

0

a

1

a

3

a

5

. . . . . . . . .

.

0

a

0

a

2

a

4

. . . . . . . . .

.

0

0

a

1

a

3

...

.

0

0

a

0

a

2

...

.

... ... ... ...

... .

0

0

0

0

. . . . . . . . .

a

m

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

.

Ðàçìåð îïðåäåëèòåëÿ ñîâïàäàåò ñî ñòåïåíüþ m ìíîãî÷ëå-

íà (ñì. ãëàâíóþ äèàãîíàëü).

Îðò áèíîðìàëè b [1, ñ. 16], [37, ñ. 7]. Ââîäèòñÿ òàê, ÷òîáû

âìåñòå ñ îðòîì êàñàòåëüíîé τ è îðòîì íîðìàëè n òðè

âåêòîðà {τ , n, b} ïðåäñòàâëÿëè ñîáîé ïðàâûé îðòîíîð-

ìèðîâàííûé áàçèñ: b=[τ ,n].

Îðò ãëàâíîé íîðìàëè (îðò íîðìàëè) n [1, ñ. 16],

[37, ñ. 7]. Íàïðàâëåí ê öåíòðó êðèâèçíû òðàåêòîðèè

òî÷êè öåíòðó îêðóæíîñòè, àïïðîêñèìèðóþùåé òðà-

åêòîðèþ â äàííîé òî÷êå. Îïðåäåëÿåòñÿ ôîðìóëîé

K = dτ /ds = Kn = n/ρ,

ãäå K âåêòîð êðèâèçíû, Ê åãî âåëè÷èíà, ρ ðàäèóñ

êðèâèçíû (ðàäèóñ àïïðîêñèìèðóþùåé îêðóæíîñòè), s

äëèíà äóãè òðàåêòîðèè.

Îðò êàñàòåëüíîé τ [1, ñ. 16], [37, ñ. 7]. Îðò, ðàñïîëîæåí-

íûé íà êàñàòåëüíîé ê òðàåêòîðèè òî÷êè. Îïðåäåëÿåòñÿ

ôîðìóëîé τ = dr (s) /ds, ãäå r (s) ðàäèóñ-âåêòîð êàê

ôóíêöèÿ äëèíû äóãè s.

Îðò íîðìàëè. Ñì. îðò ãëàâíîé áèíîðìàëè.

34

Îðòîãîíàëüíàÿ ñèñòåìà êðèâîëèíåéíûõ êîîðäèíàò

[22, ñ. 28], [37, ñ. 11]. Ñèñòåìà, ó êîòîðîé âåêòîðû ëî-

êàëüíîãî áàçèñà ïîïàðíî ïåðïåíäèêóëÿðíû.

Îðòîíîðìèðîâàííûé áàçèñ [13, ñ. 15], [37, ñ. 9]. Â ïðî-

ñòðàíñòâå ôèêñèðóþòñÿ òàêèå ÷åòûðå òî÷êè O, A

1

, A

2

,

A

3

, ÷òî äëÿ áàçèñíûõ âåêòîðîâ i

k

= OA

k

âûïîëíÿåòñÿ

(

i

k

,

i

l

) = δ

kl

=

½

1, k = l,
0, k 6= l.

Îñíîâíîé êðèòåðèé êàíîíè÷íîñòè ïðåîáðàçîâàíèÿ

[8, ñ. 131], [36, ñ. 193]. Ïðåîáðàçîâàíèå ˜q = ˜q(t, q, p),

˜

p = ˜

p (t, q, p)

ÿâëÿåòñÿ êàíîíè÷åñêèì òîãäà è òîëüêî òî-

ãäà, êîãäà ñóùåñòâóþò òàêàÿ âàëåíòíîñòü c = const è

òàêàÿ ïðîèçâîäÿùàÿ ôóíêöèÿ F, ÷òî â ñèëó ïðåîáðàçîâà-

íèÿ q, p ↔ ˜q, ˜p ñïðàâåäëèâî òîæäåñòâî

n

P

i=1

˜

p

i

d˜

q

i

− ˜

Hdt = c

µ

n

P

i=1

p

i

dq

i

− Hdt

¶

− dF

.

Îñü âèíòà (îñü ìèíèìàëüíûõ ìîìåíòîâ, öåíòðàëüíàÿ

îñü) [1, ñ. 355], [37, ñ. 39]. Ãëàâíûé ìîìåíò îòíîñè-

òåëüíî òî÷åê ýòîé îñè ðàñïîëîæåí íà ýòîé îñè.

Îñü äèíàìè÷åñêîé ñèììåòðèè â òî÷êå O òâ¼ðäîãî òåëà

[1, ñ. 200], [37, ñ. 96]. Ýëëèïñîèä èíåðöèè â òî÷êå O

ýëëèïñîèä âðàùåíèÿ âîêðóã ýòîé îñè.

Îñü ìèíèìàëüíûõ ìîìåíòîâ. Òî æå, ÷òî îñü âèíòà.
Îòäåëèìàÿ êîîðäèíàòà [8, ñ. 142], [37, ñ. 142]. Îáîáù¼ííàÿ

êîîðäèíàòà q

k

íàçûâàåòñÿ îòäåëèìîé, åñëè îò íå¼ è îò

ñîîòâåòñòâóþùåãî åé îáîáù¼ííîãî èìïóëüñà p

k

ôóíêöèÿ

Ãàìèëüòîíà çàâèñèò ñëåäóþùèì îáðàçîì:
H (t, z, q

1

, . . . , q

k−1

, q

k+1

, . . . , q

n

, p

1

, . . . , p

k−1

, p

k+1

, . . . , p

n

)

,

z = f (q

k

, p

k

)

. Îòäåëèìàÿ êîîðäèíàòà ïîðîæäàåò ïåðâûé

èíòåãðàë f (q

k

, p

k

) = c

ñîîòâåòñòâóþùåé ãàìèëüòîíîâîé

ñèñòåìû.

35

Îòêëèê ñèñòåìû. Òî æå, ÷òî âûíóæäåííîå äâèæåíèå.
Îòíîñèòåëüíàÿ ñêîðîñòü Vîòí (V

r

) [1, ñ. 32],

[37, ñ. 23]. Ñêîðîñòü îòíîñèòåëüíî ïîäâèæíîãî ïðîñòðàí-

ñòâà.

Îòíîñèòåëüíîå äâèæåíèå [1, ñ. 31], [37, ñ. 22]. Äâèæåíèå

îòíîñèòåëüíî ïîäâèæíîãî ïðîñòðàíñòâà.

Îòíîñèòåëüíîå óñêîðåíèå Wîòí (W

r

) [1, ñ. 33],

[37, ñ. 23]. Óñêîðåíèå îòíîñèòåëüíî ïîäâèæíîãî ïðîñòðàí-

ñòâà.

Îòðèöàòåëüíî îïðåäåë¼ííàÿ ôóíêöèÿ. Òî æå, ÷òî îïðåäåë¼ííî-

îòðèöàòåëüíàÿ ôóíêöèÿ.

Îòðèöàòåëüíî ïîñòîÿííàÿ (îòðèöàòåëüíî ïîëóîïðåäå-

ë¼ííàÿ) ôóíêöèÿ [22, ñ. 535], [28, ñ. 11],

[36, ñ. 85]. Äëÿ ôóíêöèè â íåêîòîðîé îáëàñòè, ñîäåð-
æàùåé òî÷êó x = 0, âûïîëíÿåòñÿ V (x)

½

= 0, x = 0,
6 0, x 6= 0.

Ïàðà [1, ñ. 364], [34, ñ. 17], [37, ñ. 36]. Äâà âåêòîðà a è −a,

ðàñïîëîæåííûå íà ïàðàëëåëüíûõ ïðÿìûõ.

Ïàðàìåòðû

Ðîäðèãà-Ãàìèëüòîíà

[33,

ñ.

28],

[37, ñ. 85]. Êîýôôèöèåíòû λ

0

, λ

1

, λ

2

, λ

3

ðàçëîæåíèÿ

Λ = λ

0

+

3

P

k=1

λ

k

i

k

êâàòåðíèîíà ïî áàçèñó i

1

, i

2

, i

3

, ñâÿ-

çàííîìó ñ ñèñòåìîé îòñ÷¼òà. Ïî ôîðìóëå e

k

= Λ ◦ i

k

◦ ˜

Λ

çàäàþò ïîëîæåíèå îðòîâ e

1

, e

2

, e

3

, ñâÿçàííûõ ñ òåëîì.

Ïàðàìåòðû

ðåãóëÿðíîé

ïðåöåññèè

[1,

ñ.

207],

[34, ñ. 191], [37, ñ. 29]. Óãëîâàÿ ñêîðîñòü ñîáñòâåííîãî

âðàùåíèÿ, óãëîâàÿ ñêîðîñòü ïðåöåññèè, óãîë íóòàöèè.

Ïàðà ÷èñòûõ (ìãíîâåííûõ) âðàùåíèé [1, ñ. 373],

[34, ñ. 39], [37, ñ. 32]. Ïàðà óãëîâûõ ñêîðîñòåé ω è −ω,

çàäàþùèõ ÷èñòûå (ìãíîâåííûå) âðàùåíèÿ. Ýêâèâàëåíò-

íà ïîñòóïàòåëüíîìó äâèæåíèþ.

36

Ïåðâûé çàêîí Êåïëåðà [1, ñ. 93], [22, ñ. 246],

[37, ñ. 68]. Ïëàíåòû äâèæóòñÿ ïî ýëëèïñàì, â ôîêóñàõ

êîòîðûõ íàõîäèòñÿ Ñîëíöå.

Ïåðâûé çàêîí Íüþòîíà [1, ñ. 45], [22, ñ. 87],

[37, ñ. 48] Èçîëèðîâàííàÿ ìàòåðèàëüíàÿ òî÷êà â èíåð-

öèàëüíîé ñèñòåìå îòñ÷¼òà äâèæåòñÿ ñ ïîñòîÿííîé ñêî-

ðîñòüþ.

Ïåðâûé èíòåãðàë [1, ñ. 273], [22, ñ. 160], [36, ñ. 137].

Ôóíêöèÿ f (t, x), êîòîðàÿ ïðè ïîäñòàíîâêå â íå¼ ëþáîãî

ðåøåíèÿ x (t) ñèñòåìû îáûêíîâåííûõ äèôôåðåíöèàëüíûõ

óðàâíåíèé â íîðìàëüíîì âèäå ˙x = ϕ (t, x), x ∈ R

n

,

ñî-

õðàíÿåò êàê ôóíêöèÿ t ñâî¼ çíà÷åíèå:

f (t, x (t)) = f (t

0

, x

0

) =

const.

Ïåðåìåííûå Ãàìèëüòîíà. Òî æå, ÷òî ãàìèëüòîíîâû ïåðå-

ìåííûå.

Ïåðåìåííûå Ëàãðàíæà. Òî æå, ÷òî ëàãðàíæåâû ïåðåìåí-

íûå.

Ïåðåìåííûå ñîñòîÿíèÿ [36, ñ. 5]. Ïåðåìåííûå, îïðåäåëÿ-

þùèå â ñîâîêóïíîñòè ñîñòîÿíèå ìåõàíè÷åñêîé ñèñòåìû

ïîëîæåíèÿ è ñêîðîñòè ìàòåðèàëüíûõ òî÷åê ñèñòåìû:

îáîáù¼ííûå êîîðäèíàòû q

i

, îáîáù¼ííûå ñêîðîñòè ˙q

i

èëè

îáîáù¼ííûå êîîðäèíàòû q

i

, îáîáù¼ííûå èìïóëüñû p

i

.

Ïåðåíîñíàÿ ñèëà èíåðöèè [1, ñ. 107], [37, ñ. 49]. Âû÷èñ-

ëÿåòñÿ ïî ôîðìóëå Jïåð = −mWïåð, ãäå m ìàññà ìà-

òåðèàëüíîé òî÷êè, Wïåð ïåðåíîñíîå óñêîðåíèå.

Ïåðåíîñíàÿ ñêîðîñòü Vïåð (V

e

) [1, ñ. 31], [37, ñ. 23].

Ñêîðîñòü ïðè äâèæåíèè ñîâìåñòíî ñ ïîäâèæíûì ïðî-

ñòðàíñòâîì (â êà÷åñòâå òî÷êè òâ¼ðäîãî òåëà).

Ïåðåíîñíîå äâèæåíèå [1, ñ. 31], [37, ñ. 22]. Äâèæåíèå ïî-

äâèæíîãî ïðîñòðàíñòâà.

37

Ïåðåíîñíîå

óñêîðåíèå

W

(W

e

)

[1,

ñ.

33],

[37, ñ. 23]. Óñêîðåíèå ïðè äâèæåíèè ñîâìåñòíî ñ ïîäâèæ-

íûì ïðîñòðàíñòâîì (â êà÷åñòâå òî÷êè òâ¼ðäîãî òåëà).

Ïåðåõîäíîé ïðîöåññ [12, ñ. 41], [36, ñ. 133]. Íà ñèñòåìó

â ïîëîæåíèè ðàâíîâåñèÿ ïîäà¼òñÿ âõîäíîå âîçäåéñòâèå
åäèíè÷íàÿ ñòóïåíüêà: Q (t)

½

= 0, t < 0,
= 1, t > 0. Ïåðåõîäíîé

ïðîöåññ äâèæåíèå ñèñòåìû äëÿ çíà÷åíèé t > 0, áëèçêèõ

ê t = 0 (äî âûõîäà íà óñòàíîâèâøèéñÿ ïðîöåññ).

Ïåðèîä ãàðìîíè÷åñêîãî êîëåáàíèÿ [6, ÷. 1, ñ. 59],

[32, ñ. 530]. Íàèìåíüøèé ïðîìåæóòîê âðåìåíè, ÷åðåç êî-

òîðûé

ñèñòåìà,

ñîâåðøàþùàÿ

êîëåáàíèå

x = A sin (ωt + α)

, âîçâðàùàåòñÿ â íà÷àëüíîå ñîñòîÿíèå.

Âû÷èñëÿåòñÿ ïî ôîðìóëå T =

2π

ω

.

Ïëå÷î ïàðû [1, ñ. 364], [34, ñ. 17], [37, ñ. 36]. Ðàññòîÿíèå

ìåæäó ïàðàëëåëüíûìè ïðÿìûìè, íà êîòîðûõ ðàñïîëîæå-

íû ýëåìåíòû a è −a ïàðû.

Ïëîñêîå äâèæåíèå [1, ñ. 36], [34, ñ. 44], [37, ñ. 54]. Äâè-

æåíèå äâóìåðíîãî òâ¼ðäîãî òåëà â ïëîñêîñòè.

Ïëîñêîïàðàëëåëüíîå äâèæåíèå [1, ñ. 36], [34, ñ. 44],

[37, ñ. 54]. Äâèæåíèå êàæäîé òî÷êè òâ¼ðäîãî òåëà ñî-

âåðøàåòñÿ â ïëîñêîñòè, ïàðàëëåëüíîé ôèêñèðîâàííîé ïëîñ-

êîñòè.

Ïëîòíîñòü ñòàòèñòè÷åñêîãî àíñàìáëÿ [1, ñ. 311],

[8, ñ. 127], [36, ñ. 184]. ρ =

µ

v

,

ãäå v âåëè÷èíà ìàëîãî

îáú¼ìà â ôàçîâîì ïðîñòðàíñòâå, µ êîëè÷åñòâî íàõîäÿ-

ùèõñÿ â îáú¼ìå ýêçåìïëÿðîâ ñòàòèñòè÷åñêîãî àíñàìáëÿ.

Ïîäâèæíîå ïðîñòðàíñòâî [1, ñ. 30], [37, ñ. 22]. Â ñëîæíîì

äâèæåíèè ïîäâèæíîå ïðîñòðàíñòâî ïåðåìåùàåòñÿ îòíî-

ñèòåëüíî ñèñòåìû îòñ÷¼òà (ïåðåíîñíîå äâèæåíèå), â ïî-

38

äâèæíîì ïðîñòðàíñòâå ïåðåìåùàþòñÿ ìàòåðèàëüíûå òî÷-

êè (îòíîñèòåëüíîå äâèæåíèå).

Ïîëå âñåìèðíîãî òÿãîòåíèÿ (íüþòîíîâñêîå ãðàâèòàöè-

îííîå ïîëå) [1, ñ. 90], [22, ñ. 98], [37, ñ. 67]. Ïîëå
ñ ïîòåíöèàëüíîé ýíåðãèåé Π

=

−γ

M m

r

, ãäå

γ = 6.67 · 10

−8

ñì

3

ã · ñåê

2

óíèâåðñàëüíàÿ ïîñòîÿííàÿ òÿãî-

òåíèÿ, M ìàññà ðàñïîëîæåííîãî â íåïîäâèæíîé òî÷êå

Ñîëíöà, m ìàññà ñîâåðøàþùåé äâèæåíèå ìàòåðèàëü-

íîé òî÷êè, r ðàññòîÿíèå òî÷êè äî Ñîëíöà.

Ïîëíàÿ ìåõàíè÷åñêàÿ ýíåðãèÿ [1, ñ. 78], [37, ñ. 61]. Âû-

÷èñëÿåòñÿ ïî ôîðìóëå E = T + Π, ãäå T , Π êèíåòè÷å-

ñêàÿ è ïîòåíöèàëüíàÿ ýíåðãèè.

Ïîëíûé

èíòåãðàë

óðàâíåíèÿ

Ãàìèëüòîíà-ßêîáè

[1,

ñ.

335],

[37,

ñ.

220].

Ðåøåíèå

S (t, q

1

, . . . , q

n

, α

1

, . . . , α

n

)

óðàâíåíèÿ Ãàìèëüòîíà-ßêîáè

(q

1

, . . . , q

n

îáîáù¼ííûå êîîðäèíàòû, α

1

, . . . , α

n

ïðîèç-

âîëüíûå

ïîñòîÿííûå),

óäîâëåòâîðÿþùåå

óñëîâèþ

det

°

°

°

°

∂

2

S (t, q, α)

∂q

i

∂α

k

°

°

°

° 6= 0.

Ïîëîæåíèå ðàâíîâåñèÿ [1, ñ. 214], [36, ñ. 71]. Ïîëîæåíèå

ìåõàíè÷åñêîé ñèñòåìû íàçûâàåòñÿ ïîëîæåíèåì ðàâíîâå-

ñèÿ, åñëè òî÷êè ñèñòåìû, ïîìåùåííûå â ýòî ïîëîæåíèå ñ

íóëåâûìè ñêîðîñòÿìè, ïðîäîëæàò îñòàâàòüñÿ â ýòîì ïî-

ëîæåíèè.

Ïîëîæèòåëüíî îïðåäåë¼ííàÿ ôóíêöèÿ. Òî æå, ÷òî îïðåäåë¼ííî-

ïîëîæèòåëüíàÿ ôóíêöèÿ.

Ïîëîæèòåëüíî ïîñòîÿííàÿ (ïîëîæèòåëüíî ïîëóîïðåäå-

ë¼ííàÿ) ôóíêöèÿ [22, ñ. 535], [28, ñ. 11],

[36, ñ. 85]. Äëÿ ôóíêöèè â íåêîòîðîé îáëàñòè, ñîäåð-

39

æàùåé òî÷êó x = 0, âûïîëíÿåòñÿ V (x)

½

= 0, x = 0,
> 0, x 6= 0.

Ïîëóãëàâíàÿ

ôóíêöèÿ

Ãàìèëüòîíà

V

¡

t, q, p

0

¢

[36, ñ. 211]. Äåéñòâèå ïî Ãàìèëüòîíó

W =

t

R

t

0

L

¡

s, q(s, q

0

, p

0

), ˙q(s, q

0

, p

0

)

¢

ds

âû÷èñëÿåòñÿ íà îáùåì ðåøåíèè q

¡

t, q

0

, p

0

¢

, p

¡

t, q

0

, p

0

¢

óðàâíåíèé Ãàìèëüòîíà.  ðåçóëüòàò âû÷èñëåíèÿ ïîäñòàâ-

ëÿåòñÿ íàéäåííàÿ èç îáùåãî ðåøåíèÿ âåêòîð-ôóíêöèÿ
q

0

= q

0

¡

t, q, p

0

¢

.

Ïîëóñâîáîäíîå

êàíîíè÷åñêîå

ïðåîáðàçîâàíèå

[36, ñ. 202]. Êàíîíè÷åñêîå ïðåîáðàçîâàíèå, óäîâëåòâîðÿ-
þùåå óñëîâèþ det

°

°

°

°

∂ ˜

p

i

(t, q, p)

∂p

k

°

°

°

° 6= 0.

Ïîñòóëàò Ìàêñâåëëà [5, ñ. 115], [20, ñ. 114],

[36, ñ. 69]. Ïîâåäåíèå ýëåêòðîìåõàíè÷åñêîé ñèñòåìû îï-

ðåäåëÿåòñÿ óðàâíåíèÿìè Ëàãðàíæà, â êîòîðûå ïîäñòàâ-

ëåíû ôóíêöèè: êèíåòè÷åñêàÿ ýíåðãèÿ, ïîòåíöèàëüíàÿ

ýíåðãèÿ, äèññèïàòèâíàÿ ôóíêöèÿ Ðåëåÿ, îáîáù¼ííûå ñè-

ëû, ñîîòâåòñòâóþùèå íåïîòåíöèàëüíûì è íåäèññèïàòèâ-

íûì ñèëàì. Âñå óêàçàííûå ôóíêöèè åñòü ñóììû ñîîòâåò-

ñòâóþùèõ ôóíêöèé äëÿ ýëåêòðè÷åñêîé ÷àñòè ñèñòåìû è

äëÿ ìåõàíè÷åñêîé.

Ïîëþñ [22, ñ. 50]. Ïðîèçâîëüíàÿ ôèêñèðîâàííàÿ òî÷êà òâ¼ð-

äîãî òåëà.

Ïîñòóïàòåëüíîå äâèæåíèå òâ¼ðäîãî òåëà [1, ñ. 22],

[37, ñ. 32]. Äâèæåíèå, ïðè êîòîðîì ëþáàÿ ïðÿìàÿ, ñâÿ-

çàííàÿ ñ òåëîì, ïåðåìåùàåòñÿ ïàðàëëåëüíî ñàìîé ñåáå.

Ïîòåíöèàëüíàÿ ñèëà [1, ñ. 60], [37, ñ. 60]. Ñèëà

F

i

(t,

r

1

, . . . ,

r

N

)

, äåéñòâóþùàÿ íà ìàòåðèàëüíóþ òî÷êó,

îïðåäåë¼ííóþ ðàäèóñ-âåêòîðîì r

i

, íàçûâàåòñÿ ïîòåíöè-

àëüíîé, åñëè ñóùåñòâóåò òàêàÿ ñêàëÿðíàÿ ôóíêöèÿ

40

Π (t,

r

1

, . . . ,

r

N

)

ïîòåíöèàëüíàÿ ýíåðãèÿ, ÷òî ñïðàâåä-

ëèâû ðàâåíñòâà

F

i

(t,

r

1

, . . . ,

r

N

) = − grad

i

Π (t,

r

1

, . . . ,

r

N

) =

= −∇

i

Π (t,

r

1

, . . . ,

r

N

)

,

ãäå grad

i

Π (t,

r

1

, . . . ,

r

N

) = ∇

i

Π (t,

r

1

, . . . ,

r

N

)

ãðàäèåíò

ïîòåíöèàëüíîé ýíåðãèè ïî ïåðåìåííûì, ñîîòâåòñòâóþ-

ùèì ðàäèóñ-âåêòîðó r

i

.

Ïîòåíöèàëüíàÿ ýíåðãèÿ [1, ñ. 60], [37, ñ. 60]. Ôóíêöèÿ

Π (t,

r

1

, . . . ,

r

N

)

, êîòîðàÿ îïðåäåëÿåò ïîòåíöèàëüíûå ñè-

ëû F

i

(t,

r

1

, . . . ,

r

N

)

, äåéñòâóþùèå íà ìàòåðèàëüíûå òî÷-

êè, îïðåäåë¼ííûå ðàäèóñ-âåêòîðàìè r

i

.

Ïîòåíöèàëüíîå ñèëîâîå ïîëå [1, ñ. 60], [37, ñ. 60]. Ñè-

ëîâîå ïîëå, â êîòîðîì îïðåäåëÿþùàÿ ïîëå ñèëà ÿâëÿåòñÿ

ïîòåíöèàëüíîé.

Ïðèâåä¼ííûé êèíåòè÷åñêèé ìîìåíò (èíòåãðàë ïëîùà-

äåé) [22, ñ. 242], [37, ñ. 64]. Ñîõðàíÿþùàÿñÿ âî âðåìÿ
äâèæåíèÿ â öåíòðàëüíîì ïîëå âåëè÷èíà c =

K

0

m

= r

2

˙

ϕ

,

ãäå K

0

êèíåòè÷åñêèé ìîìåíò îòíîñèòåëüíî öåíòðà ïî-

ëÿ, m ìàññà ìàòåðèàëüíîé òî÷êè, r, ϕ ïîëÿðíûå

êîîðäèíàòû.

Ïðèëîæåííûé âåêòîð [1, ñ. 351], [37, ñ. 36]. Âåêòîð ñ ôèê-

ñèðîâàííîé íà÷àëüíîé òî÷êîé.

Ïðèíöèï âèðòóàëüíûõ ïåðåìåùåíèé. Òî æå, ÷òî îáùåå

óðàâíåíèå ñòàòèêè.

Ïðèíöèï âîçìîæíûõ ïåðåìåùåíèé. Òî æå, ÷òî êðèòåðèé

ðàâíîâåñèÿ ñòàöèîíàðíî çàäàííîé ñèñòåìû.

Ïðèíöèï Ãàìèëüòîíà. Òî æå, ÷òî âàðèàöèîííûé ïðèíöèï

Ãàìèëüòîíà.

Ïðèíöèï Ãàìèëüòîíà-Îñòðîãðàäñêîãî. Òî æå, ÷òî âàðè-

àöèîííûé ïðèíöèï Ãàìèëüòîíà.

41

Ïðèíöèï

Ìîïåðòþè-Ëàãðàíæà

[1,

ñ.

344],

[36, ñ. 178]. Ïóòü ˜q(q

1

)

â êîîðäèíàòíîì ïðîñòðàíñòâå

ÿâëÿåòñÿ ïðÿìûì â òîì è òîëüêî â òîì ñëó÷àå, åñëè ïðè

ëþáîì âàðüèðîâàíèè q (q

1

, α)

ïðè íåèçìåííûõ ãðàíè÷íûõ

òî÷êàõ äëÿ âàðèàöèè äåéñòâèÿ ïî Ëàãðàíæó âûïîëíÿåò-

ñÿ δW

∗

|

α=0

= 0

.

Ïðèíöèï ñòàöèîíàðíîãî äåéñòâèÿ Ãàìèëüòîíà. Òî æå,

÷òî âàðèàöèîííûé ïðèíöèï Ãàìèëüòîíà.

Ïðèíöèï ñóïåðïîçèöèè [1, ñ. 248], [36, ñ. 129]. Åñëè âíåø-

íèì âîçäåéñòâèÿì Q

α

(t)

íà ëèíåéíóþ ñèñòåìó ñîîòâåò-

ñòâóþò îòêëèêè q

α

(t)

, òî âíåøíåìó âîçäåéñòâèþ

P

α

Q

α

(t)

ñîîòâåòñòâóåò îòêëèê

P

α

q

α

(t)

.

Ïðîâàðüèðîâàòü ôóíêöèþ. Òî æå, ÷òî âàðüèðîâàíèå ôóíê-

öèè.

Ïðîèçâîäÿùàÿ ôóíêöèÿ êàíîíè÷åñêîãî ïðåîáðàçîâàíèÿ

[1, ñ. 329], [36, ñ. 193]. Ôóíêöèÿ F â îñíîâíîì êðèòåðèè

êàíîíè÷íîñòè ïðåîáðàçîâàíèÿ ãàìèëüòîíîâûõ ïåðåìåí-

íûõ.

Ïðîñòðàíñòâî

ñîñòîÿíèé

(ôàçîâîå

ïðîñòðàíñòâî)

[1, ñ. 213], [36, ñ. 4]. 2n-ìåðíîå ïðîñòðàíñòâî ñ êîîðäèíà-

òàìè q

1

, . . . , q

n

, ˙q

1

, . . . , ˙q

n

(îáîáù¼ííûå êîîðäèíàòû, îáîá-

ù¼ííûå

ñêîðîñòè)

èëè

ñ

êîîðäèíàòàìè

q

1

, . . . , q

n

, p

1

, . . . , p

n

(îáîáù¼ííûå

êîîðäèíàòû,

îáîáù¼ííûå èìïóëüñû). Äëÿ ñèñòåìû îáûêíîâåííûõ äèô-

ôåðåíöèàëüíûõ óðàâíåíèé â íîðìàëüíîì âèäå ïðîñòðàí-

ñòâî ñ êîîðäèíàòàìè x

1

, . . . , x

n

.

Ïðÿìîé ïóòü [1, ñ. 286], [36, ñ. 144]. Ãðàôèê äâèæåíèÿ â

îäíîì èç ïðîñòðàíñòâ (êîîðäèíàòíîì, ðàñøèðåííîì êî-

îðäèíàòíîì è ò. ä.) ÿâëÿþùèéñÿ ðåøåíèåì óðàâíåíèé äè-

íàìèêè (óðàâíåíèé Ëàãðàíæà, óðàâíåíèé Ãàìèëüòîíà è

ò. ä.).

42

Ïóàíñî èíòåðïðåòàöèÿ. Ñì. Èíòåðïðåòàöèÿ Ïóàíñî.
Ðàáîòà ñèë [1, ñ. 58], [36, ñ. 56]. Ðàáîòà A

12

ñèë F

i

(t,

r, ˙r)

íà ïóòè r

i

(t)

ñèñòåìû ìàòåðèàëüíûõ òî÷åê çà âðåìÿ

t ∈ [t

1

, t

2

]

âû÷èñëÿåòñÿ ïî ôîðìóëå

A

12

=

t

2

R

t

1

N

P

i=1

(

F

i

, d

r

i

) =

=

t

2

R

t

1

N

P

i=1

(

F

i

(t,

r (t) , ˙r (t)) , V

i

(t)) dt.

Ðàäèàëüíîå óñêîðåíèå W

r

[26, ñ. 17], [37, ñ. 27]. Ïðîåê-

öèÿ óñêîðåíèÿ íà ðàäèóñ-âåêòîð. Âåëè÷èíà â ïîëÿðíûõ

êîîðäèíàòàõ ðàâíà W

r

= ¨

r − ˙

ϕ

2

r

.

Ðàäèóñ êðèâèçíû [1, ñ. 17], [37, ñ. 7]. Ðàäèóñ îêðóæíîñòè,

àïïðîêñèìèðóþùåé êðèâóþ â äàííîé òî÷êå.

Ðàäèóñ-âåêòîð r [22, ñ. 21], [37, ñ. 6]. Íà÷àëüíàÿ òî÷êà íåïî-

äâèæíà â ñèñòåìå îòñ÷¼òà, êîíå÷íàÿ òî÷êà îïðåäåëÿåò

ïîëîæåíèå ìàòåðèàëüíîé òî÷êè.

Ðàçäåëåíèå ïåðåìåííûõ â óðàâíåíèè Ãàìèëüòîíà-ßêîáè

[22, ñ. 375], [36, ñ. 221].  êà÷åñòâå ïîëíîãî èíòåãðàëà

ôóíêöèè S (t, q

1

, . . . , q

n

, α

1

, . . . , α

n

)

ìíîãèõ ïåðåìåííûõ

îòûñêèâàåòñÿ êîìáèíàöèÿ ôóíêöèé, êàæäàÿ èç êîòîðûõ

ÿâëÿåòñÿ

ôóíêöèåé

îäíîé

ïåðåìåííûõ.

Íàïðèìåð,

àääèòèâíàÿ

êîìáèíàöèÿ

S = S

0

(t, α) + S

1

(q

1

, α) + . . . + S

n

(q

n

, α)

, ìóëüòèïëèêàòèâ-

íàÿ êîìáèíàöèÿ S = S

0

(t, α) × S

1

(q

1

, α) × · · · × S

n

(q

n

, α)

.

Ðàñøèðåííîå êîîðäèíàòíîå ïðîñòðàíñòâî [1, ñ. 214],

[36, ñ. 4]. (n+1)-ìåðíîå ïðîñòðàíñòâî ñ êîîðäèíàòàìè
t, q

1

, . . . , q

n

(âðåìÿ, îáîáù¼ííûå êîîðäèíàòû).

Ðàñøèðåííîå ïðîñòðàíñòâî ñîñòîÿíèé (ðàñøèðåííîå ôà-

çîâîå ïðîñòðàíñòâî) [1, ñ. 214], [36, ñ. 4]. (2n+1)-

ìåðíîå

ïðîñòðàíñòâî

ñ

êîîðäèíàòàìè

43

t, q

1

, . . . , q

n

, ˙q

1

, . . . , ˙q

n

(âðåìÿ, îáîáù¼ííûå êîîðäèíàòû,

îáîáù¼ííûå

ñêîðîñòè)

èëè

ñ

êîîðäèíàòàìè

t, q

1

, . . . , q

n

, p

1

, . . . , p

n

(âðåìÿ, îáîáù¼ííûå êîîðäèíàòû,

îáîáù¼ííûå èìïóëüñû).

Ðàñøèðåííîå ôàçîâîå ïðîñòðàíñòâî. Òî æå, ÷òî ðàñøè-

ðåííîå ïðîñòðàíñòâî ñîñòîÿíèé.

Ðåàêöèÿ ñâÿçåé [1, ñ. 159], [36, ñ. 36]. Ñèëû, áëàãîäàðÿ

êîòîðûì âûïîëíÿþòñÿ íàëîæåííûå íà ñèñòåìó ìåõàíè-

÷åñêèå ñâÿçè.

Ðåàêöèÿ ñèñòåìû íà âíåøíåå âîçäåéñòâèå. Òî æå, ÷òî

âûíóæäåííîå äâèæåíèå.

Ðåãóëÿðíàÿ ïðåöåññèÿ òâ¼ðäîãî òåëà [1, ñ. 207],

[34, ñ. 191], [37, ñ. 29]. Ñëîæíîå äâèæåíèå, ïðè êî-

òîðîì ïîäâèæíîå ïðîñòðàíñòâî âðàùàåòñÿ âîêðóã íåïî-

äâèæíîé îñè ñ ïîñòîÿííîé óãëîâîé ñêîðîñòüþ ωïåð (óã-

ëîâàÿ ñêîðîñòü ïðåöåññèè), à îòíîñèòåëüíûì äâèæåíè-

åì ÿâëÿåòñÿ òàêæå âðàùåíèå âîêðóã íåïîäâèæíîé îñè ñ

ïîñòîÿííîé óãëîâîé ñêîðîñòüþ ωîòí (óãëîâàÿ ñêîðîñòü

ñîáñòâåííîãî âðàùåíèÿ). Îñè, âîêðóã êîòîðûõ ïðîèñõî-

äÿò âðàùåíèÿ, ïåðåñåêàþòñÿ. Õàðàêòåðèçóåòñÿ ïàðàìåò-

ðàìè ðåãóëÿðíîé ïðåöåññèè.

Ðåçàëÿ òåîðåìà [22, ñ. 76], [37, ñ. 8]. Äëÿ âåêòîðà

a (t) = AB

ñïðàâåäëèâà ôîðìóëà

da

dt

= ˙a = V

B

− V

A

,

ãäå V

A

, V

B

ñêîðîñòè ãðàíè÷íûõ òî÷åê.

Ðåîíîìíûå ñâÿçè. Òî æå, ÷òî íåñòàöèîíàðíûå ñâÿçè.
Ñâîáîäíîå äâèæåíèå òâ¼ðäîãî òåëà [1, ñ. 176],

[37, ñ. 108]. Åäèíñòâåííûå ìåõàíè÷åñêèå ñâÿçè, íàëî-

æåííûå íà ïîëîæåíèÿ òî÷åê òåëà: ðàññòîÿíèå ìåæäó ëþ-

áûìè äâóìÿ òî÷êàìè íåèçìåííî.

44

Ñâîáîäíîå êàíîíè÷åñêîå ïðåîáðàçîâàíèå [1, ñ. 329],

[36, ñ. 200]. Êàíîíè÷åñêîå ïðåîáðàçîâàíèå, óäîâëåòâîðÿ-
þùåå óñëîâèþ det

°

°

°

°

∂ ˜

q

i

(t, q, p)

∂p

k

°

°

°

° 6= 0.

Ñâîáîäíûé âåêòîð [34, ñ. 9], [37, ñ. 36]. Íàïðàâëåííûé

îòðåçîê ñ ïðîèçâîëüíîé òî÷êîé ïðèëîæåíèÿ.

Ñåêòîðíàÿ ñêîðîñòü [22, ñ. 243], [37, ñ. 64]. Ñêîðîñòü çà-

ìåòàíèÿ ïëîùàäè ðàäèóñ-âåêòîðîì.

Ñèëà [1, ñ. 90], [37, ñ. 48]. Ñèëîé, äåéñòâóþùåé íà ìàòå-

ðèàëüíóþ òî÷êó, (ìåðîé âçàèìîäåéñòâèÿ ñ äðóãèìè òî÷-

êàìè) íàçûâàåòñÿ ïðîèçâîäíàÿ ïî âðåìåíè îò èìïóëüñà

òî÷êè.

Ñèëà âñåìèðíîãî òÿãîòåíèÿ [1, ñ. 57], [37, ñ. 67]. Ñèëà

âçàèìîäåéñòâèÿ ìåæäó ìàòåðèàëüíûìè òî÷êàìè ñ ìàñ-

ñàìè m è M:

F = −γ

mM

r

3

r

,

ãäå γ = 6.67 · 10

−11

Í· ì

2

·

êã

−2

âñåìèðíàÿ ïîñòîÿííàÿ,

r

âåêòîð, ïðîâåäåííûé îò òî÷êè ñ ìàññîé M ê òî÷êå ñ

ìàññîé m. Ïðèâåäåíà ñèëà, äåéñòâóþùàÿ íà òî÷êó ñ ìàñ-

ñîé m.

Ñèëà èíåðöèè [1, ñ. 107], [37, ñ. 49]. Ñèëà, êîòîðóþ äî-

ïîëíèòåëüíî íóæíî ïðèëîæèòü ê ìàòåðèàëüíîé òî÷êå,

÷òîáû âòîðîé çàêîí Íüþòîíà áûë ñïðàâåäëèâ â íåèíåð-

öèàëüíîé ñèñòåìå îòñ÷¼òà

Ñèëà èíåðöèè êîðèîëèñîâà. Ñì. êîðèîëèñîâà ñèëà èíåðöèè.
Ñèëà èíåðöèè ïåðåíîñíàÿ. Ñì. ïåðåíîñíàÿ ñèëà èíåðöèè.
Ñèëà öåíòðàëüíàÿ [1, ñ. 62], [37, ñ. 63]. Äåéñòâóåò íà ìà-

òåðèàëüíóþ òî÷êó è êîëëèíåàðíà åå ðàäèóñ-âåêòîðó.

Ñèëû âíåøíèå. Ñì. âíåøíèå ñèëû.
Ñèëû âíóòðåííèå. Ñì. âíóòðåííèå ñèëû.

45

Ñèëîâàÿ ôóíêöèÿ [1, ñ. 60], [37, ñ. 630]. Ôóíêöèÿ, îáðàòíàÿ

ïî çíàêó ïîòåíöèàëüíîé ýíåðãèè.

Ñèëîâîå ïîëå [1, ñ. 59], [37, ñ. 60]. Ñèëû F

i

(t, r

1

, . . . , r

N

)

,

äåéñòâóþùèå íà îòäåëüíûå ìàòåðèàëüíûå òî÷êè, íå çà-

âèñÿò îò ñêîðîñòåé òî÷åê.

Ñèíõðîííûé äèôôåðåíöèàë [22, ñ. 38]. Òî æå, ÷òî èçî-

õðîííûé äèôôåðåíöèàë.

Ñèñòåìà â èíâîëþöèè. Òî æå, ÷òî èíâîëþöèîííàÿ ñèñòåìà.
Ñèñòåìà Êåíèãà [34, ñ. 156], [37, ñ. 57]. Ñèñòåìà (òð¼õìåð-

íîå ïðîñòðàíñòâî) äâèæåòñÿ ïîñòóïàòåëüíî, îäíà èç å¼

òî÷åê ñîâïàäàåò ñ öåíòðîì èíåðöèè ñèñòåìû ìàòåðè-

àëüíûõ òî÷åê.

Ñèñòåìà êîíñåðâàòèâíàÿ. Ñì. êîíñåðâàòèâíàÿ ñèñòåìà.
Ñèñòåìà

ëèíåéíîãî

ïðèáëèæåíèÿ

[1,

ñ.

218],

[36, ñ. 127]. Ïðàâûå ÷àñòè ñèñòåìû â íîðìàëüíîì âè-

äå ˙x = ϕ (x) ,

x ∈ R

n

,

ϕ (0) = 0

, ðàñêëàäûâàþò â

ðÿäû â îêðåñòíîñòè ðåøåíèÿ x = 0 è îñòàâëÿþò òîëüêî

ëèíåéíûå ñëàãàåìûå.

Ñèñòåìà ìàòåðèàëüíûõ òî÷åê [1, ñ. 43], [37, ñ. 50]. Ñè-

ñòåìà ñîñòîèò èç N > 1 ìàòåðèàëüíûõ òî÷åê.

Ñèñòåìà îáûêíîâåííûõ äèôôåðåíöèàëüíûõ óðàâíåíèé

â íîðìàëüíîì âèäå (â íîðìàëüíîé ôîðìå Êîøè)

[11, ñ. 9], [36, ñ. 35]. Ñèñòåìà ˙x = ϕ (t, x), x ∈ R

n

, ó êîòî-

ðîé â ëåâîé ÷àñòè íàõîäÿòñÿ ïðîèçâîäíûå, â ïðàâîé ÷àñòè

ôóíêöèè îò íåçàâèñèìîé è çàâèñèìûõ ïåðåìåííûõ.

Ñèñòåìà îòñ÷¼òà [1, ñ. 11], [37, ñ. 9]. Òð¼õìåðíîå åâêëèäîâî

ïðîñòðàíñòâî, îòíîñèòåëüíî êîòîðîãî ñîâåðøàåò äâèæå-

íèå ìåõàíè÷åñêàÿ ñèñòåìà.

Ñèñòåìà îòñ÷¼òà èíåðöèàëüíàÿ. Ñì. èíåðöèàëüíàÿ ñèñòå-

ìà îòñ÷¼òà.

46

Ñèñòåìà îòñ÷¼òà íåèíåðöèàëüíàÿ. Ñì. íåèíåðöèàëüíàÿ ñè-

ñòåìà îòñ÷¼òà.

Ñèñòåìà ïåðåìåííîãî ñîñòàâà [1, ñ. 110], [37, ñ. 72]. Ñè-

ñòåìà, ó êîòîðîé âî âðåìÿ äâèæåíèÿ ïðîèñõîäèò ïðèõîä

è óõîä ìàòåðèàëüíûõ òî÷åê.

Ñêàëÿðíàÿ ÷àñòü êâàòåðíèîíà [33, ñ. 14], [37, ñ. 83].

×àñòü λ

0

êâàòåðíèîíà

Λ = λ

0

+ λ

1

i

1

+ λ

2

i

2

+ λ

3

i

3

= λ

0

+ λ

.

Ñêàëÿðíûé èíâàðèàíò [1, ñ. 355], [37, ñ. 39]. Ñêàëÿðíîå

ïðîèçâåäåíèå (R, M

O

)

ãëàâíîãî âåêòîðà R íà ãëàâíûé

ìîìåíò M

O

ìíîæåñòâà ñêîëüçÿùèõ âåêòîðîâ.

Ñêëåðîíîìíûå

ñâÿçè

(ñòàöèîíàðíûå

ñâÿçè)

[1, ñ. 153], [36, ñ. 21]. Ìåõàíè÷åñêèå ñâÿçè, óñëîâèÿ
f

l

(r

i

, V

i

) 6 0

êîòîðûõ íå ñîäåðæàò ÿâíî âðåìåíè t.

Ñêîáêà Ëàãðàíæà [1, ñ. 327], [8, ñ. 159]. Ñîïîñòàâëåíèå

ôóíêöèÿì

ãàìèëüòîíîâûõ

ïåðåìåííûõ

ϕ

i

(t, q, p)

,

ψ

i

(t, q, p)

, i = 1, n, ôóíêöèè

[q

j

, p

k

] =

n

P

i=1

µ

∂ϕ

i

∂q

j

∂ψ

i

∂p

k

−

∂ϕ

i

∂p

k

∂ψ

i

∂q

j

¶

.

Ñêîáêà Ïóàññîíà [1, ñ. 274], [8, ñ. 87], [37, ñ. 138]. Ñîïî-

ñòàâëåíèå ôóíêöèÿì ãàìèëüòîíîâûõ ïåðåìåííûõ ϕ (t, q, p),
ψ (t, q, p)

ôóíêöèè

(ϕ, ψ) =

n

P

i=1

µ

∂ϕ

∂q

i

∂ψ

∂p

i

−

∂ϕ

∂p

i

∂ψ

∂q

i

¶

.

Ñêîëüçÿùèé âåêòîð [1, ñ. 351], [37, ñ. 36]. Íàïðàâëåííûé

îòðåçîê, êîòîðûé ìîæíî ïåðåìåùàòü âäîëü ëèíèè äåé-

ñòâèÿ.

Ñêîðîñòü ìàòåðèàëüíîé òî÷êè [1, ñ. 14], [37, ñ. 7]. Îïðåäå-

ëÿåòñÿ ïî ôîðìóëå V = dr/dt = ˙r, ãäå r ðàäèóñ-âåêòîð

òî÷êè.

47

Ñëîæíîå äâèæåíèå [1, ñ. 30], [37, ñ. 22]. Ïîäâèæíîå ïðî-

ñòðàíñòâî ïåðåìåùàåòñÿ îòíîñèòåëüíî ñèñòåìû îòñ÷¼-

òà (ïåðåíîñíîå äâèæåíèå), â ïîäâèæíîì ïðîñòðàíñòâå

ïåðåìåùàþòñÿ ìàòåðèàëüíûå òî÷êè (îòíîñèòåëüíîå äâè-

æåíèå).

Ñëó÷àé Êîâàëåâñêîé äâèæåíèÿ òâåðäîãî òåëà. Ñì. Êî-

âàëåâñêîé ñëó÷àé .

Ñëó÷àé Ëàãðàíæà äâèæåíèÿ òâåðäîãî òåëà. Ñì. Ëàãðàí-

æà ñëó÷àé äâèæåíèÿ òâåðäîãî òåëà.

Ñëó÷àé Ýéëåðà äâèæåíèÿ òâåðäîãî òåëà [1, ñ. 199],

[37, ñ. 100]. Òâ¼ðäîå òåëî ñîâåðøàåò äâèæåíèå ñ íåïî-

äâèæíîé òî÷êîé O. Ãëàâíûé ìîìåíò M

O

âíåøíèõ ñèë

îòíîñèòåëüíî íåïîäâèæíîé òî÷êè ðàâåí íóëþ.

Ñîáñòâåííûé êâàòåðíèîí [33, ñ. 33], [37, ñ. 89]. Áàçèñ i

k

íîðìèðîâàííûì êâàòåðíèîíîì Λ = λ

0

+

3

P

k=1

λ

k

i

k

ïåðåâî-

äèòñÿ â áàçèñ e

k

, êîòîðûé íîðìèðîâàííûì êâàòåðíèîíîì

M = µ

0

+

3

P

k=1

µ

k

e

k

ïåðåâîäèòñÿ â áàçèñ n

k

. Â ñîáñòâåííîì

êâàòåðíèîíå M

∗

= µ

0

+

3

P

k=1

µ

k

i

k

ïî îòíîøåíèþ ê êâàòåð-

íèîíó M êîýôôèöèåíòû ðàçëîæåíèÿ ïî áàçèñó e

k

ïðè-

ïèñûâàþòñÿ èñõîäíîìó áàçèñó i

k

.

Ñîáñòâåííûé àìïëèòóäíûé âåêòîð (ôîðìà ãëàâíîãî êî-

ëåáàíèÿ) [36, ñ. 100]. Àìïëèòóäíûé âåêòîð â ãëàâíîì

êîëåáàíèè.

Ñîáñòâåííàÿ ÷àñòîòà [17, ñ. 438], [36, ñ. 100]. Êðóãîâàÿ

÷àñòîòà â ãëàâíîì êîëåáàíèè.

Ñîãëàñîâàííûå êîíòóðû [36, ñ. 171]. Êîíòóðû C

0

è C

1

îõâàòûâàþò òðóáêó ïðÿìûõ ïóòåé è ïàðàìåòðèçîâàíû

êàæäûé ïàðàìåòðîì α òàê, ÷òî çíà÷åíèþ ïàðàìåòðà α

48

ñîîòâåòñòâóþò òî÷êè êîíòóðîâ C

0

, C

1

, ðàñïîëîæåííûå íà

îäíîì è òîì æå ïðÿìîì ïóòè.

Ñîïðîâîæäàþùèé òð¼õãðàííèê [1, ñ. 15], [37, ñ. 6]. Áàçèñ

â êàæäîé òî÷êå òðàåêòîðèè, ñîñòîÿùèé èç îðòîâ êàñà-

òåëüíîé, íîðìàëè è áèíîðìàëè.

Ñîïðÿæåííûå êèíåòè÷åñêèå ôîêóñû. Òî æå, ÷òî êèíåòè-

÷åñêèå ôîêóñû.

Ñîïðÿæ¼ííûé êâàòåðíèîí [33, ñ. 38], [37, ñ. 84]. Êâà-

òåðíèîíó Λ = λ

0

+

3

P

k=1

λ

k

i

k

ñîîòâåòñòâóåò ñîïðÿæ¼ííûé

êâàòåðíèîí ˜Λ = λ

0

−

3

P

k=1

λ

k

i

k

.

Ñîñòîÿíèå ìàòåðèàëüíîé òî÷êè [17, ñ. 32], [36, ñ. 5]. Ïî-

ëîæåíèå è ñêîðîñòü òî÷êè îòíîñèòåëüíî ñèñòåìû îòñ÷¼-

òà.

Ñòàòèñòè÷åñêèé àíñàìáëü [1, ñ. 311], [36, ñ. 1841]. Ìíîæå-

ñòâî ãàìèëüòîíîâûõ ñèñòåì, ó êîòîðûõ ñîâïàäàþò ôóíê-

öèè Ãàìèëüòîíà, íî ðàçëè÷àþòñÿ íà÷àëüíûå äàííûå
q

0

, p

0

.

Ñòàòè÷åñêèé âèíò (äèíàìà) [1, ñ. 371], [36, ñ. 40]. Âèíò,

ñîîòâåòñòâóþùèé ìíîæåñòâó ñèë.

Ñòàöèîíàðíî çàäàííàÿ ñèñòåìà [36, ñ. 26]. Ðàäèóñ-âåêòîð

r

i

(q)

ëþáîé òî÷êè ìåõàíè÷åñêîé ñèñòåìû åñòü ôóíêöèÿ

òîëüêî îáîáù¼ííûõ êîîðäèíàò (íåò ÿâíîé çàâèñèìîñòè

îò âðåìåíè t).

Ñòàöèîíàðíî

ïîòåíöèàëüíîå

ñèëîâîå

ïîëå

[36, ñ. 60]. Ïîòåíöèàëüíîå ñèëîâîå ïîëå, äëÿ êîòîðîãî

îïðåäåëÿþùàÿ ïîëå ïîòåíöèàëüíàÿ ýíåðãèÿ Π (r

1

, . . . ,

r

N

)

íå çàâèñèò ÿâíî îò âðåìåíè.

Ñòàöèîíàðíûå ñâÿçè. Òî æå, ÷òî ñêëåðîíîìíûå ñâÿçè.

49

Ñòðóêòóðíàÿ ôîðìóëà äëÿ óðàâíåíèé Ëàãðàíæà

[36, ñ. 12]. Ïðîìåæóòî÷íàÿ ôîðìóëà äëÿ óðàâíåíèé Ëà-

ãðàíæà â ïðîèçâîëüíûõ ïàðàìåòðàõ (íå îáÿçàòåëüíî â

îáîáù¼ííûõ êîîðäèíàòàõ).

Òàíãåíöèàëüíîå (êàñàòåëüíîå) óñêîðåíèå. Ñì. êàñàòåëü-

íîå óñêîðåíèå.

Òâ¼ðäîå òåëî [1, ñ. 17], [37, ñ. 9]. Òàêàÿ ñîâîêóïíîñòü ìàòå-

ðèàëüíûõ òî÷åê, ÷òî ðàññòîÿíèå ìåæäó ëþáûìè äâóìÿ

íåèçìåííî.

Òåíçîð èíåðöèè [1, ñ. 181], [36, ñ. 94]. Ìàòðèöà

^

I

=





I

1

−I

12

−I

13

−I

21

I

2

−I

23

−I

31

−I

32

I

3



 êâàäðàòè÷íîé ôîðìû

I

e

=

3

P

k=1

I

k

α

2

k

− 2

P

k<l

I

kl

α

k

α

l

, ãäå I

e

ìîìåíò èíåðöèè

òâ¼ðäîãî òåëà îòíîñèòåëüíî îñè, îðèåíòèðîâàííîé îðòîì
e

, α

k

ïðîåêöèè îðòà e íà êîîðäèíàòíûå îñè, I

k

ìî-

ìåíòû èíåðöèè îòíîñèòåëüíî êîîðäèíàòíûõ îñåé, I

kl

öåíòðîáåæíûå ìîìåíòû èíåðöèè.

Òåîðåìà

Áàðáàøèíà-Êðàñîâñêîãî

[12,

ñ.

122],

[28, ñ. 49], [36, ñ. 109]. Ïóñòü ñóùåñòâóåò òàêàÿ ôóíê-

öèÿ V (x), ÷òî äëÿ íå¼ â íåêîòîðîé îáëàñòè, ñîäåðæàùåé

òî÷êó x = 0, è ñèñòåìû ˙x = ϕ (x) , x ∈ R

n

, èìåþùåé ðå-

øåíèå x(t) ≡ 0, âûïîëíÿåòñÿ:

1. V (x) ïîëîæèòåëüíî îïðåäåë¼ííàÿ ôóíêöèÿ;
2. W (x) = ˙V (x) =

n

P

i=1

∂V (x)

∂x

i

ϕ

i

(x)

½

= 0, x ∈ M,
< 0, x /

∈ M, ãäå

M

íåêîòîðîå ìíîæåñòâî;

3. åäèíñòâåííûì ðåøåíèåì, ïðèíàäëåæàùèì M ïðè t ∈
[0, ∞)

ÿâëÿåòñÿ x (t) ≡ 0.

Òîãäà x (t) ≡ 0 àñèìïòîòè÷åñêè óñòîé÷èâîå ïî Ëÿïó-

íîâó ðåøåíèå. Åñëè óñëîâèå 1. çàìåíèòü óñëîâèåì

1*.V (0) = 0; ∀δ > 0, ∃|x

0

| < δ

, V (x

0

) < 0

,

òî ðåøåíèå x (t) ≡ 0 íåóñòîé÷èâî ïî Ëÿïóíîâó.

50

Òåîðåìà Ãþéãåíñà Õ., Øòåéíåðà ß. Ñì. Ãþéãåíñà Õ.,

Øòåéíåðà ß. òåîðåìà.

Òåîðåìà: çàêîí ñîõðàíåíèÿ ïîëíîé ìåõàíè÷åñêîé ýíåð-

ãèè [1, ñ. 78], [37, ñ. 61]. Ïîëíàÿ ìåõàíè÷åñêàÿ ýíåðãèÿ
E = T + Π

êîíñåðâàòèâíîé ñèñòåìû ñîõðàíÿåòñÿ âî âðå-

ìÿ äâèæåíèÿ.

Òåîðåìà Êåíèãà äëÿ ñèñòåìû ìàòåðèàëüíûõ òî÷åê. Ñì.

Êåíèãà òåîðåìà äëÿ ñèñòåìû ìàòåðèàëüíûõ òî÷åê.

Òåîðåìà Êåíèãà äëÿ òâ¼ðäîãî òåëà. Ñì. Êåíèãà òåîðåìà

äëÿ òâ¼ðäîãî òåëà.

Òåîðåìà Êîðèîëèñà. Ñì. Êîðèîëèñà òåîðåìà.
Òåîðåìà Ëàãðàíæà-Äèðèõëå [1, ñ. 231], [36, ñ. 92]. Ïóñòü

â íåêîòîðîé ∆-îêðåñòíîñòè òî÷êè q

0

= 0

êîîðäèíàòíîãî

ïðîñòðàíñòâà ïîòåíöèàëüíàÿ ýíåðãèÿ Π (q) êîíñåðâàòèâ-

íîé

ñèñòåìû

èìååò

â

ïîëîæåíèè

q

0

= 0

ñòðîãèé ìèíèìóì. Òîãäà q

0

= 0

óñòîé÷èâîå ïî

Ëÿïóíîâó ïîëîæåíèå ðàâíîâåñèÿ.

Òåîðåìà Ëèóâèëëÿ î ïåðâûõ èíòåãðàëàõ â èíâîëþöèè

[22, ñ. 381], [36, ñ. 225]. Ïóñòü äëÿ ïåðâûõ èíòåãðàëîâ
w

i

(t, q, p) = α

i

, i = 1, n, 2n-ìåðíîé ãàìèëüòîíîâîé ñè-

ñòåìû âûïîëíÿåòñÿ:

à) (w

i

, w

k

) = 0,

i, k = 1, n,

((·, ·) ñêîáêà Ïóàññîíà)

ïåðâûå èíòåãðàëû íàõîäÿòñÿ â èíâîëþöèè;

á) óðàâíåíèÿ w

i

(t, q, p) = α

i

,

i = 1, n,

ðàçðåøèìû îòíî-

ñèòåëüíî p: p

i

= ψ

i

(t, q, α)

.

Òîãäà, íå âûõîäÿ çà ðàìêè àëãåáðàè÷åñêèõ îïåðàöèé è

êâàäðàòóð, ïî ôóíêöèÿì w

i

(t, q, p)

, i = 1, n, âû÷èñëÿþò-

ñÿ: ïîëíûé èíòåãðàë S (t, q, α) óðàâíåíèÿ Ãàìèëüòîíà-

ßêîáè;

äîïîëíèòåëüíûå

ïåðâûå

èíòåãðàëû

w

n+i

(t, q, p) = α

n+i

, i = 1, n; îáùåå ðåøåíèå q

i

(t, α)

,

p

i

(t, α)

, i = 1, n, óðàâíåíèé Ãàìèëüòîíà.

51

Òåîðåìà Ëèóâèëëÿ î ñîõðàíåíèè âåëè÷èíû ôàçîâîãî

îáú¼ìà [1, ñ. 311], [36, ñ. 180]. Ïóñòü ïðàâûå ÷àñòè

ñèñòåìû îáûêíîâåííûõ äèôôåðåíöèàëüíûõ óðàâíåíèé â

íîðìàëüíîì âèäå ˙x = ϕ (t, x), x ∈ R

n

, óäîâëåòâîðÿþò

óñëîâèþ

div ϕ (t, x) =

n

P

i=1

∂ϕ

i

(t, x)

∂x

i

= 0

(óñëîâèå âûïîëíåíî äëÿ ãàìèëüòîíîâûõ ñèñòåì). Òîãäà

ïðè ïåðåíîñå ôàçîâîãî îáú¼ìà ðåøåíèÿìè ñèñòåìû ñîõðà-

íÿåòñÿ åãî âåëè÷èíà.

Òåîðåìà Ëè Õóà÷æóíà [1, ñ. 316], [36, ñ. 185]. Ñëåäóþùèå

äâà óòâåðæäåíèÿ ýêâèâàëåíòíû:
à) èíòåãðàë J =

H

C

n

P

i=1

{A

i

(t, q, p) δq

i

+ B

i

(t, q, p) δp

i

}

àíà-

ëîãè÷íî

èíòåãðàëüíîìó

èíâàðèàíòó

Ïóàíêàðå

H

C

n

P

i=1

p

i

δq

i

èíòåãðàëüíûé èíâàðèàíò;

á) ñóùåñòâóåò òàêîå ÷èñëî ñ è òàêàÿ ôóíêöèÿ
F (t, q, p)

, ÷òî ïîäûíòåãðàëüíûå âûðàæåíèÿ ñâÿçàíû ñî-

îòíîøåíèåì

n

P

i=1

{A

i

(t, q, p) δq

i

+ B

i

(t, q, p) δp

i

}

=

= c

n

P

i=1

p

i

δq

i

− δF (t, q, p) ,

ãäå δF (t, q, p) èçîõðîííûé äèôôåðåíöèàë (t ôèêñè-

ðîâàííûé ïàðàìåòð).

Òåîðåìà Ëÿïóíîâà îá óñòîé÷èâîñòè íóëåâîãî ðåøåíèÿ

ñèñòåìû

â

íîðìàëüíîì

âèäå

[28,

ñ.

22],

[36, ñ. 85]. Ïóñòü â ∆-îêðåñòíîñòè íóëåâîãî ðåøåíèÿ àâ-

òîíîìíîé ñèñòåìû â íîðìàëüíîì âèäå ˙x = ϕ (x) , x ∈ R

n

,

ñóùåñòâóåò ïîëîæèòåëüíî îïðåäåë¼ííàÿ ôóíêöèÿ V (x)

òàêàÿ, ÷òî å¼ ïðîèçâîäíàÿ ˙V (x) â ñèëó ñèñòåìû ˙x = ϕ (x),
x ∈ R

n

, îòðèöàòåëüíî ïîñòîÿííàÿ. Òîãäà íóëåâîå ðåøå-

íèå óñòîé÷èâî ïî Ëÿïóíîâó.

52

Òåîðåìà Ëÿïóíîâà î íåóñòîé÷èâîñòè ïîëîæåíèÿ ðàâíî-

âåñèÿ

êîíñåðâàòèâíîé

ñèñòåìû

(ïåðâàÿ)

[1, ñ. 233], [36, ñ. 93]. Ïóñòü äëÿ ïîòåíöèàëüíîé ýíåð-

ãèè Π (q) (Π (0) = 0) êîíñåðâàòèâíîé ñèñòåìû â íåêî-

òîðîì ïîëîæåíèè q∗ âûïîëíÿåòñÿ Π

2

(q∗) < 0

, ãäå Π

2

ñîâîêóïíîñòü ñëàãàåìûõ â Π (q) âòîðîãî ïîðÿäêà (îòñóò-

ñòâèå ïðè q

0

= 0

ìèíèìóìà ó Π (q), âêëþ÷àÿ íåñòðîãèé).

Òîãäà ïîëîæåíèå ðàâíîâåñèÿ q

0

= 0

íåóñòîé÷èâî ïî Ëÿ-

ïóíîâó.

Òåîðåìà Ëÿïóíîâà î íåóñòîé÷èâîñòè ïîëîæåíèÿ ðàâíî-

âåñèÿ êîíñåðâàòèâíîé ñèñòåìû (âòîðàÿ) [1, ñ. 233],

[36, ñ. 93]. Ïóñòü Π

m

ñîâîêóïíîñòü ñëàãàåìûõ â ïî-

òåíöèàëüíîé ýíåðãèè Π (q) (Π (0) = 0) êîíñåðâàòèâíîé

ñèñòåìû íàèìåíüøåé ñòåïåíè m > 2, è ôóíêöèÿ Π

m

(q)

îòðèöàòåëüíî îïðåäåëåíà. Òîãäà ïîëîæåíèå ðàâíîâåñèÿ
q

0

= 0

íåóñòîé÷èâî ïî Ëÿïóíîâó.

Òåîðåìà ͼòåð Ýììè [1, ñ. 296], [36, ñ. 153]. Ïóñòü îäíî-

ïàðàìåòðè÷åñêàÿ ãðóïïà

_

t =

_

t (t, q, τ )

,

_

q

i

=

_

q

i

(t, q, τ )

,

i = 1, n,

ãðóïïà âàðèàöèîííûõ ñèììåòðèé äëÿ ëà-

ãðàíæåâîé ñèñòåìû, îïðåäåë¼ííîé ôóíêöèåé Ëàãðàíæà
L (t, q, ˙q)

. Òîãäà ó ñèñòåìû åñòü ïåðâûé èíòåãðàë

w =

n

P

i=1

p

i

η

i

− ξH

, ãäå p

i

è H, ñâÿçàííûå ñ ôóíêöèåé Ëà-

ãðàíæà L (t, q, ˙q) îáîáù¼ííûé èìïóëüñ è ãàìèëüòîíèàí,

ôóíêöèè ξ è η

i

âû÷èñëÿþòñÿ ïî óðàâíåíèÿì ãðóïïû

ξ (t, q) =

∂

_

t (t, q, τ )

∂τ

¯

¯

¯

¯

¯

τ =0

, η

i

(t, q) =

∂

_

q

i

(t, q, τ )

∂τ

¯

¯

¯

¯

¯

τ =0

.

Òåîðåìà îá àñèìïòîòè÷åñêîé óñòîé÷èâîñòè ïîëîæåíèÿ

ðàâíîâåñèÿ äèññèïàòèâíîé ñèñòåìû [1, ñ. 236],

[36, ñ. 112]. Ïóñòü q

0

= 0

èçîëèðîâàííîå ïîëîæåíèå

ðàâíîâåñèÿ ñòàöèîíàðíî çàäàííîé îïðåäåë¼ííî-äèññèïà-

òèâíîé ñèñòåìû. Ïóñòü ïîòåíöèàëüíàÿ ýíåðãèÿ èìååò

ïðè q

0

= 0

ñòðîãèé ìèíèìóì. Òîãäà q

0

= 0

àñèìï-

òîòè÷åñêè óñòîé÷èâîå ïîëîæåíèå ðàâíîâåñèÿ.

53

Òåîðåìà îá óãëîâîé ñêîðîñòè [1, ñ. 24], [22, ñ. 59]

[36, ñ. 9], [37, ñ. 17]. Â êàæäûé ìîìåíò âðåìåíè t ñóùå-

ñòâóåò òàêîé åäèíñòâåííûé âåêòîð ω (óãëîâàÿ ñêîðîñòü),

÷òî ñêîðîñòè ëþáûõ äâóõ òî÷åê òâ¼ðäîãî òåëà B è C

ñâÿçàíû ñîîòíîøåíèåì V

B

=

V

C

+ [ω, ρ]

, ãäå ρ = CB.

Òåîðåìà îá óñòîé÷èâîñòè íóëåâîãî ðåøåíèÿ ëèíåéíîé

àâòîíîìíîé ñèñòåìû [11, ñ. 278, 279], [36, ñ. 112].
λ

k

= µ

k

+ iν

k

êîðíè õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ

ëèíåéíîé àâòîíîìíîé ñèñòåìû ˙x = Dx, x ∈ R

n

,

D =

const.

1. {∀µ

k

= Reλ

k

< 0} ⇔ {x ≡ 0

àñèìïòîòè÷åñêè

óñòîé÷èâîå ðåøåíèå ñèñòåìû ˙x = Dx};

2. {∃µ

k

= Reλ

k

> 0} ⇒ {x ≡ 0

íåóñòîé÷èâîå ðåøåíèå

ñèñòåìû ˙x = Dx};

3. {µ

k

= Reλ

k

< 0, k = 1, r < n, µ

k

= Reλ

k

= 0, k =

r + 1, n} ⇒ {x ≡ 0

óñòîé÷èâîå ïî Ëÿïóíîâó èëè

íåóñòîé÷èâîå ðåøåíèå ñèñòåìû ˙x = Dx}.

Òåîðåìà îá óñòîé÷èâîñòè ïî ëèíåéíîìó ïðèáëèæåíèþ

[1, ñ. 236], [36, ñ. 127]

1. Ïóñòü äëÿ êîðíåé λ

k

= µ

k

+ iν

k

õàðàêòåðèñòè÷åñêî-

ãî óðàâíåíèÿ ñèñòåìû ëèíåéíîãî ïðèáëèæåíèÿ ˙x = Dx,
x ∈ R

n

, D = const, âûïîëíÿåòñÿ ∀µ

k

= Reλ

k

< 0

. Òî-

ãäà ðåøåíèå x ≡ 0 íåëèíåéíîé ñèñòåìû ˙x = ϕ (x) =
Dx + R (x)

(R (x) íåëèíåéíûå ñëàãàåìûå) àñèìïòîòè-

÷åñêè óñòîé÷èâî.

2. Ïóñòü äëÿ êîðíåé λ

k

= µ

k

+ iν

k

õàðàêòåðèñòè÷åñêî-

ãî óðàâíåíèÿ ñèñòåìû ëèíåéíîãî ïðèáëèæåíèÿ ˙x = Dx,
x ∈ R

n

, D = const, âûïîëíÿåòñÿ ∃µ

k

= Reλ

k

> 0

. Òîãäà

ðåøåíèå x ≡ 0 íåëèíåéíîé ñèñòåìû ˙x = ϕ (x) = Dx+R (x)

(R (x) íåëèíåéíûå ñëàãàåìûå) íåóñòîé÷èâî.

Òåîðåìà î ñëîæåíèè ñêîðîñòåé â ñëîæíîì äâèæåíèè

[1, ñ. 32], [37, ñ. 24]. Àáñîëþòíàÿ ñêîðîñòü Vàáñ òî÷êè

â ñëîæíîì äâèæåíèè åñòü ñóììà ïåðåíîñíîé è îòíîñè-

òåëüíîé ñêîðîñòåé: Vàáñ = Vïåð + Vîòí.

54

Òåîðåìà î ñëîæåíèè óñêîðåíèé â ñëîæíîì äâèæåíèè

(òåîðåìà Êîðèîëèñà) . Ñì. Êîðèîëèñà òåîðåìà.

Òåîðåìà Ðàóñà-Ãóðâèöà. Òî æå, ÷òî êðèòåðèé Ðàóñà-Ãóðâèöà.
Òåîðåìà Ðåçàëÿ. Ñì. Ðåçàëÿ òåîðåìà.
Òåîðåìà ×åòàåâà î íåóñòîé÷èâîñòè íóëåâîãî ðåøåíèÿ

ñèñòåìû

â

íîðìàëüíîì

âèäå

[28,

ñ.

26],

[36, ñ. 85]. Ïóñòü â ε-îêðåñòíîñòè ðåøåíèÿ x (t) = 0 ñè-

ñòåìû â íîðìàëüíîì âèäå ˙x = ϕ (x) , x ∈ R

n

, ñóùåñòâóåò

îáëàñòü M (∂M ãðàíèöà îáëàñòè M), â êîòîðîé ïðè

íåêîòîðîì ÷èñëå k äëÿ ôóíêöèè V (x) âûïîëíÿåòñÿ:

1. 0 < V (x) 6 k;
2. W (x) = ˙V (x) =

n

P

i=1

∂V (x)

∂x

i

ϕ

i

(x) > 0

;

3. {V (x) > V

0

} ⇒ {∃l > 0, W (x) > l}

;

4. {x = 0} ∈ ∂M;

5. {x ∈ ∂M, |x| < ε} ⇒ {V (x) = 0}.

Òîãäà ðåøåíèå x (t) = 0 ñèñòåìû ˙x = ϕ (x) , x ∈ R

n

íåóñòîé÷èâî ïî Ëÿïóíîâó.

Òåîðåìà ×åòàåâà î íåóñòîé÷èâîñòè ïîëîæåíèÿ ðàâíîâå-

ñèÿ

êîíñåðâàòèâíîé

ñèñòåìû

[1,

ñ.

234],

[36, ñ. 94]. Ïóñòü ïîòåíöèàëüíàÿ ýíåðãèÿ Π (q)

(Π (0) = 0) êîíñåðâàòèâíîé ñèñòåìû îäíîðîäíàÿ ôóíê-

öèÿ, è â ïîëîæåíèè q∗ ñèñòåìû âûïîëíÿåòñÿ Π (q∗) < 0

(îòñóòñòâèå ïðè q

0

= 0

ìèíèìóìà, âêëþ÷àÿ íåñòðîãèé).

Òîãäà ïîëîæåíèå ðàâíîâåñèÿ q

0

= 0

íåóñòîé÷èâî ïî Ëÿ-

ïóíîâó.

Òåîðåìà Ýììè ͼòåð. Òî æå, ÷òî òåîðåìà ͼòåð Ýììè.
Òåîðåìà ßêîáè-Ïóàññîíà [1, ñ. 275], [36, ñ. 119]. Ñêîá-

êà Ïóàññîíà (ϕ, ψ) ïåðâûõ èíòåãðàëîâ ϕ (t, q, p) = c

1

,

ψ (t, q, p) = c

2

ãàìèëüòîíîâîé ñèñòåìû ïåðâûé èíòå-

ãðàë òîé æå ãàìèëüòîíîâîé ñèñòåìû.

55

Òðàåêòîðèÿ

ìàòåðèàëüíîé

òî÷êè

[22,

ñ.

20],

[37, ñ. 6]. Ãîäîãðàô ðàäèóñ-âåêòîðà.

Òðàíñâåðñàëüíîå óñêîðåíèå [26, ñ. 17], [37, ñ. 27] Â ïëîñ-

êîì äâèæåíèè ïðîåêöèÿ óñêîðåíèÿ ìàòåðèàëüíîé òî÷êè

íà íàïðàâëåíèå, ïåðïåíäèêóëÿðíîå ðàäèóñ-âåêòîðó. Âå-

ëè÷èíà â ïîëÿðíûõ êîîðäèíàòàõ ðàâíà W

ϕ

= ¨

ϕr + 2 ˙

ϕ ˙r

.

Òðåòèé çàêîí Êåïëåðà [1, ñ. 93], [37, ñ. 69]. Îòíîøåíèå

êâàäðàòà âðåìåíè îáðàùåíèÿ ïëàíåòû âîêðóã Ñîëíöà ê

êóáó áîëüøîé ïîëóîñè òðàåêòîðèè îäèíàêîâî äëÿ âñåõ

ïëàíåò îäíîé è òîé æå Ñîëíå÷íîé ñèñòåìû.

Òðåòèé çàêîí Íüþòîíà [1, ñ. 57], [37, ñ. 50]. Ñèëû âçàèìî-

äåéñòâèÿ ìåæäó äâóìÿ ìàòåðèàëüíûìè òî÷êàìè ïðåä-

ñòàâëÿþò ñîáîé âåêòîðíûé íóëü.

Òðóáêà ïðÿìûõ ïóòåé [1, ñ. 302], [36, ñ. 171]. Â ðàñøèðåí-

íîì ôàçîâîì ïðîñòðàíñòâå ðàññìàòðèâàåòñÿ çàìêíóòûé

êîíòóð, è ÷åðåç êàæäóþ åãî òî÷êó t

0

, q

0

, p

0

(êàê íà÷àëü-

íóþ) ïðîâîäèòñÿ ïðÿìîé ïóòü ðåøåíèå ãàìèëüòîíî-

âîé ñèñòåìû.

Óãëîâàÿ ñêîðîñòü òâ¼ðäîãî òåëà [1, ñ. 24], [22, ñ. 59],

[36, ñ. 9], [37, ñ. 17]. Âåêòîð, ñóùåñòâîâàíèå è åäèí-

ñòâåííîñòü êîòîðîãî óñòàíàâëèâàåòñÿ òåîðåìîé îá óãëî-

âîé ñêîðîñòè.

Óãëîâàÿ ñêîðîñòü ïðåöåññèè [1, ñ. 207], [22, ñ. 196],

[37, ñ. 29]. Ïðè ðåãóëÿðíîé ïðåöåññèè òâ¼ðäîãî òåëà

óãëîâàÿ ñêîðîñòü ïîäâèæíîãî ïðîñòðàíñòâà.

Óãëîâàÿ ñêîðîñòü ñîáñòâåííîãî âðàùåíèÿ [1, ñ. 207],

[22, ñ. 196], [37, ñ. 29]. Ïðè ðåãóëÿðíîé ïðåöåññèè òâ¼ð-

äîãî òåëà óãëîâàÿ ñêîðîñòü îòíîñèòåëüíî ïîäâèæíîãî

ïðîñòðàíñòâà.

Óãëîâàÿ ÷àñòîòà ãàðìîíè÷åñêîãî êîëåáàíèÿ. Ñì. êðóãî-

âàÿ (óãëîâàÿ, öèêëè÷åñêàÿ) ÷àñòîòà ãàðìîíè÷åñêîãî êî-

ëåáàíèÿ.

56

Óãëîâîå

óñêîðåíèå

òâ¼ðäîãî

òåëà

[1,

ñ.

23],

[37, ñ. 18]. Âû÷èñëÿåòñÿ ÷åðåç óãëîâóþ ñêîðîñòü ω ñëå-

äóþùèì îáðàçîì: ε = dω/dt = ˙ω.

Óãëû Ýéëåðà [1, ñ. 193], [37, ñ. 80]. Çàäàþò îðèåíòàöèþ áà-

çèñà e

1

, e

2

, e

3

, ñâÿçàííîãî òâ¼ðäûì òåëîì, îòíîñèòåëü-

íî áàçèñà i

1

, i

2

, i

3

, ñâÿçàííîãî ñ ñèñòåìîé îòñ÷¼òà: óãîë

íóòàöèè θ = [

i

3

, e

3

; óãîë ïðåöåññèè ψ = d

i

1

, n

; óãîë ñîá-

ñòâåííîãî âðàùåíèÿ ϕ = [

n, e

1

, ãäå n îðò, ðàñïîëîæåí-

íûé íà ëèíèè óçëîâ: n⊥i

3

, n⊥e

3

.

Óãîë íóòàöèè. Ñì. óãëû Ýéëåðà.
Óãîë ïðåöåññèè. Ñì. óãëû Ýéëåðà.
Óãîë ñîáñòâåííîãî âðàùåíèÿ. Ñì. óãëû Ýéëåðà.
Óäåðæèâàþùàÿ ñâÿçü [1, ñ. 151], [36, ñ. 21]. Îãðàíè÷åíèå

f (t, r

i

, V

i

) = 0

òèïà ðàâåíñòâà, íàëîæåííîå íà ñîñòîÿíèÿ

ìåõàíè÷åñêîé ñèñòåìû.

Óíèâàëåíòíîå

êàíîíè÷åñêîå

ïðåîáðàçîâàíèå

[1, ñ. 329], [36, ñ. 199]. Äëÿ âàëåíòíîñòè c âûïîëíÿåòñÿ
c = 1

.

Óðàâíåíèå Áèíå. Ñì. Áèíå óðàâíåíèå.
Óðàâíåíèå Ãàìèëüòîíà-ßêîáè [1, ñ. 335], [36, ñ. 191].

Ñòðîèòñÿ ïî ôóíêöèè Ãàìèëüòîíà H (t, q, p) ñëåäóþùèì
îáðàçîì:

∂S

∂t

+ H

µ

t, q,

∂S

∂q

¶

= 0

.

Óðàâíåíèå Ëÿïóíîâà [36, ñ. 123]. Óðàâíåíèå D

T

X + XD =

C

îòíîñèòåëüíî êâàäðàòíîé ÷èñëîâîé ìàòðèöû X, C è D

êâàäðàòíûå ÷èñëîâûå ìàòðèöû.

Óðàâíåíèå Ìåùåðñêîãî [1, ñ. 123], [36, ñ. 74]. Îïðåäåëÿ-

åò ïîñòóïàòåëüíîå äâèæåíèå òâ¼ðäîãî òåëà ïåðåìåííîãî

ñîñòàâà:

57

m

d

V

dt

=

Râíåøí −

n

X

i=1

dmóõ

i

dt

uóõ

i

+

r

X

k=1

dmïð

k

dt

uïð

k

,

ãäå m

ïåðåìåííàÿ ìàññà òåëà, V ñêîðîñòü òåëà, Râíåøí

ãëàâíûé âåêòîð âíåøíèõ ñèë, móõ

i

, mïð

k

óøåäøèå

è ïðèøåäøèå ê ìîìåíòó âðåìåíè t ìàññû, uóõ

i

, uïð

k

ñêîðîñòè óõîäÿùèõ è ïðèõîäÿùèõ ìàññ â ïîäâèæíîé ïî-

ñòóïàòåëüíîé ñèñòåìå, ñâÿçàííîé ñ òåëîì.

Óðàâíåíèå Íüþòîíà. Òî æå, ÷òî âòîðîé çàêîí Íüþòîíà.
Óðàâíåíèå ÷àñòîò. Òî æå, ÷òî âåêîâîå óðàâíåíèå.
Óðàâíåíèÿ Ãàìèëüòîíà. Òî æå, ÷òî ãàìèëüòîíîâà ñèñòåìà.
Óðàâíåíèÿ Ëàãðàíæà. Òî æå, ÷òî ëàãðàíæåâà ñèñòåìà.
Óðàâíåíèÿ Óèòòåêåðà [1, ñ. 340], [36, ñ. 137]. Óðàâíåíèå

H (q, p) = h

, ãäå H (q, p) ôóíêöèÿ Ãàìèëüòîíà îáîáù¼í-

íî êîíñåðâàòèâíîé ñèñòåìû, ðàçðåøàåòñÿ îòíîñèòåëüíî

îäíîãî èç îáîáù¼ííûõ èìïóëüñîâ, íàïðèìåð, p

1

:

p

1

= −K (q

1

, q

2

, . . . , q

n

, p

2

, . . . , p

n

, h)

. Ïðèíèìàÿ îáîáù¼í-

íóþ êîîðäèíàòó q

1

çà íåçàâèñèìóþ, ïî ôóíêöèè Óèò-

òåêåðà K (q

1

, q

2

, . . . , q

n

, p

2

, . . . , p

n

, h)

âû÷èñëÿþòñÿ óðàâ-

íåíèÿ Óèòòåêåðà (ãàìèëüòîíîâà ñèñòåìà):

dq

i

dq

1

=

∂K

∂p

i

,

dp

i

dq

1

= −

∂K

∂q

i

,

i = 2, n

.

Óðàâíåíèÿ Ýéëåðà [4, ñ. 24].  âàðèàöèîííîì èñ÷èñëåíèè

óðàâíåíèÿ Ëàãðàíæà íàçûâàþòñÿ óðàâíåíèÿìè Ýéëåðà.

Óðàâíåíèÿ ßêîáè [1, ñ. 341] [36, ñ. 178]. Ëàãðàíæåâà ñè-

ñòåìû

d

dq

1

∂P
∂q

0

i

−

∂P
∂q

i

= 0

, â îñíîâå êîòîðîé ëåæèò ôóíêöèÿ

ßêîáè P (q

1

, q, q

0

)

, q

1

íåçàâèñèìàÿ ïåðåìåííàÿ, øòðèõ

ïðîèçâîäíàÿ ïî íåé.

Óñêîðåíèå ìàòåðèàëüíîé òî÷êè [1, ñ. 14], [37, ñ. 8]. Îïðå-

äåëÿåòñÿ ïî ôîðìóëå W = dV/dt = ˙V = ¨r, ãäå V

ñêîðîñòü òî÷êè, r ðàäèóñ-âåêòîð òî÷êè.

58

Óñêîðåíèå Êîðèîëèñà. Ñì. êîðèîëèñîâî óñêîðåíèå.
Óñêîðåíèå ðàäèàëüíîå. Ñì. ðàäèàëüíîå óñêîðåíèå.
Óñêîðåíèå òðàíñâåðñàëüíîå. Ñì. òðàíñâåðñàëüíîå óñêîðå-

íèå.

Óñëîâèÿ ðàâíîâåñèÿ òâ¼ðäîãî òåëà [10, ñ. 257],

[36, ñ. 81]. Íåêîòîðîå ïîëîæåíèå òâ¼ðäîãî òåëà ÿâëÿåòñÿ

åãî ïîëîæåíèåì ðàâíîâåñèÿ â òîì è òîëüêî â òîì ñëó÷àå,

åñëè âûïîëíÿþòñÿ ðàâåíñòâà: R = 0, M

O

= 0

, ãäå R

ãëàâíûé âåêòîð, M

O

ãëàâíûé ìîìåíò äåéñòâóþùèõ íà

òåëî ñèë, O ïðîèçâîëüíàÿ òî÷êà òåëà.

Óñòàíîâèâøèéñÿ ïðîöåññ. Òî æå, ÷òî âûíóæäåííîå äâèæå-

íèå.

Óñòîé÷èâîñòü ïî Ëÿïóíîâó [1, ñ. 222], [36, ñ. 83]. Ðå-

øåíèå x = 0 ñèñòåìû â íîðìàëüíîì âèäå ˙x = ϕ (t, x),
x ∈ R

n

,

óñòîé÷èâî ïî Ëÿïóíîâó, åñëè äëÿ îáùåãî ðåøå-

íèÿ x (t, t

0

, x

0

)

âûïîëíÿåòñÿ: ∀ε > 0, ∀t

0

> 0, ∃δ > 0

,

∀|x

0

| < δ, ∀t > t

0

, |x (t, t

0

, x

0

) | < ε

.

Óñòîé÷èâûé ìíîãî÷ëåí [8, ñ. 196], [36, ñ. 117]. Ìíîãî÷ëåí

â

ëåâîé

÷àñòè

õàðàêòåðèñòè÷åñêîãî

óðàâíåíèÿ

a

0

λ

m

+a

1

λ

m−1

+· · ·+a

m−1

λ+a

m

= 0

íàçûâàåòñÿ óñòîé÷è-

âûì, åñëè âñå êîðíè λ

k

= µ

k

+ iν

k

õàðàêòåðèñòè÷åñêîãî

óðàâíåíèÿ ðàñïîëàãàþòñÿ â êîìïëåêñíîé ïëîñêîñòè ñëåâà

îò ìíèìîé îñè: ∀µ

k

= Reλ

k

< 0

.

Ôàçà ãàðìîíè÷åñêîãî êîëåáàíèÿ [6, ÷. 1, ñ. 59],

[32, ñ. 110]. Âûðàæåíèå ωt + α â ãàðìîíè÷åñêîì êîëå-

áàíèè x = A sin (ωt + α).

Ôàçîâàÿ õàðàêòåðèñòèêà [1, ñ. 252], [36, ñ. 132]. Çàâè-

ñèìîñòü àðãóìåíòà ψ

jk

(Ω) = arg W

jk

(iΩ)

àìïëèòóäíî-

ôàçîâîé õàðàêòåðèñòèêè W

jk

(iΩ) = R

jk

(Ω) e

iψ

jk

(Ω)

îò

ïåðåìåííîé Ω.

59

Ôàçîâûé îáú¼ì [1, ñ. 310], [36, ñ. 83]. Âåëè÷èíà îáú¼ìà

çàìêíóòîé îáëàñòè â ôàçîâîì ïðîñòðàíñòâå (ïðîñòðàí-

ñòâå ñîñòîÿíèé).

Ôàçîâûé ïîòîê ãàìèëüòîíîâîé ñèñòåìû [22, ñ. 358],

[36, ñ. 205]. Ñîâîêóïíîñòü ïðåîáðàçîâàíèé q

0

, p

0

↔ q, p

ôàçîâîãî ïðîñòðàíñòâà, êîòîðûå îïðåäåëÿþòñÿ ïðè ðàç-

íûõ ôèêñèðîâàííûõ çíà÷åíèÿõ âðåìåíè t îáùèì ðåøåíè-

åì q = q

¡

t, q

0

, p

0

¢

, p = p

¡

t, q

0

, p

0

¢

ãàìèëüòîíîâîé ñèñòå-

ìû.

Ôîêàëüíûé ïàðàìåòð [1, ñ. 92], [37, ñ. 67]. Ïîñòîÿííàÿ p

â ôîðìóëå r =

p

1 + e cos (ϕ + β)

äëÿ îðáèò â ïîëå âñåìèð-

íîãî òÿãîòåíèÿ êîíè÷åñêèõ ñå÷åíèé â ïîëÿðíûõ êîîð-

äèíàòàõ.

Ôîêóñ êèíåòè÷åñêèé. Ñì. êèíåòè÷åñêèé ôîêóñ.
Ôîðìà ãëàâíîãî êîëåáàíèÿ. Òî æå, ÷òî ñîáñòâåííûé àì-

ïëèòóäíûé âåêòîð.

Ôîðìóëà Öèîëêîâñêîãî [1, ñ. 124], [37, ñ. 75]. Ñêîðîñòü

îäíîìåðíîãî äâèæåíèÿ ðàêåòû ïðè îòñóòñòâèè âíåøíèõ
ñèë: V (t) = V

0

+u ln

m

0

m (t)

, ãäå V

0

, m

0

ñêîðîñòü è ìàññà â

íà÷àëå äâèæåíèÿ, u ñêîðîñòü èñòå÷åíèÿ ðàáî÷åãî òåëà,
m (t)

òåêóùàÿ ìàññà.

Ôóíêöèè Ëÿïóíîâà V (x) [1, ñ. 239], [36, ñ. 83]. Îïðåäåëå-

íû â íåêîòîðîé ∆−îêðåñòíîñòè íóëÿ: |x| < ∆. Äëÿ V (x)

ïðåäïîëàãàåòñÿ V (0) = 0. Èñïîëüçóþòñÿ ôóíêöèè Ëÿïó-

íîâà: çíàêîîïðåäåë¼ííûå (ïîëîæèòåëüíî, îòðèöàòåëü-

íî), çíàêîïîñòîÿííûå (ïîëîæèòåëüíî, îòðèöàòåëüíî),

çíàêîïåðåìåííûå.

Ôóíêöèÿ Ãàìèëüòîíà. Òî æå, ÷òî ãàìèëüòîíèàí.
Ôóíêöèÿ Ëàãðàíæà. Òî æå, ÷òî ëàãðàíæèàí.

60

Ôóíêöèÿ ñèëîâàÿ. Ñì. ñèëîâàÿ ôóíêöèÿ.
Ôóíêöèÿ

Óèòòåêåðà

K (q

1

, q

2

, . . . , q

n

, p

2

, . . . , p

n

, h)

[1, ñ. 340], [36, ñ. 142]. Ðåçóëüòàò ðàçðåøåíèÿ óðàâíåíèÿ
H (q, p) = h

îòíîñèòåëüíî îäíîãî èç îáîáù¼ííûõ èìïóëü-

ñîâ, íàïðèìåð, p

1

: p

1

= −K (q

1

, q

2

, . . . , q

n

, p

2

, . . . , p

n

, h)

.

H (q, p)

ôóíêöèÿ Ãàìèëüòîíà îáîáù¼ííî êîíñåðâàòèâ-

íîé ñèñòåìû.

Ôóíêöèÿ ßêîáè P (q

1

, q, q

0

)

[1, ñ. 341], [36, ñ. 178]. Âû÷èñ-

ëÿåòñÿ

ïî

ôóíêöèè

Óèòòåêåðà

K (q

1

, q

2

, . . . , q

n

, p

2

, . . . , p

n

, h)

êàê ëàãðàíæèàí ïî ãàìèëü-

òîíèàíó: P (q

1

, q, q

0

) =

n

P

k=2

p

k

q

0

k

− K

, q

1

íåçàâèñèìàÿ

ïåðåìåííàÿ, øòðèõ ïðîèçâîäíàÿ ïî íåé.

Õàðàêòåðèñòè÷åñêèé

ìíîãî÷ëåí

[1,

ñ.

220],

[36, ñ. 115]. Ìíîãî÷ëåí, ðàñïîëîæåííûé â ëåâîé ÷àñòè

õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ

a

0

λ

m

+ a

1

λ

m−1

+ · · · + a

m−1

λ + a

m

= 0

.

Õàðàêòåðèñòè÷åñêîå

óðàâíåíèå

[1,

ñ.

220],

[36, ñ. 115]. Ðåøåíèå ëèíåéíîé àâòîíîìíîé ñèñòåìû

˙x = Dx

, x ∈ R

n

, D = const, îòûñêèâàåòñÿ â âèäå x = ue

λt

,

ïîñëå ñîêðàùåíèÿ íà e

λt

îñòà¼òñÿ àëãåáðàè÷åñêîå óðàâ-

íåíèå (D − λE) u = 0 äëÿ ÷èñåë λ, u. Óðàâíåíèå èìå-

åò íåòðèâèàëüíîå ðåøåíèå u 6= 0 òîãäà è òîëüêî òîãäà,

êîãäà λ óäîâëåòâîðÿåò õàðàêòåðèñòè÷åñêîìó óðàâíåíèþ
det (D − λE) = a

0

λ

m

+ a

1

λ

m−1

+ · · · + a

m−1

λ + a

m

= 0

.

Õàðàêòåð

ýêñòðåìóìà

äåéñòâèÿ

ïî

Ãàìèëüòîíó

[4, ñ. 70], [27, ò. 2, ñ. 231], [36, ñ. 156]

Íåîáõîäèìîå óñëîâèå ìèíèìóìà. Åñëè äåéñòâèå ïî

Ãàìèëüòîíó ïðè ëþáîì âàðüèðîâàíèè ïðÿìîãî ïóòè ñ

çàêðåïëåííûìè ãðàíè÷íûìè òî÷êàìè

¡

t

0

, q

0

¢

,

¡

t

1

, q

1

¢

â

ðàñøèðåííîì êîîðäèíàòíîì ïðîñòðàíñòâå äîñòèãàåò ìè-

íèìóìà íà ïðÿìîì ïóòè, òî ïðè t

0

< t < t

1

îòñóòñòâóþò

êèíåòè÷åñêèå ôîêóñû, ñîïðÿæåííûå òî÷êå

¡

t

0

, q

0

¢

.

61

Äîñòàòî÷íîå óñëîâèå ñòðîãîãî ìèíèìóìà.

Åñëè

íà

ïðÿìîì ïóòè ïðè t

0

< t 6 t

1

îòñóòñòâóþò êèíåòè÷åñêèå

ôîêóñû, ñîïðÿæ¼ííûå íà÷àëüíîé òî÷êå

¡

t

0

, q

0

¢

, òî ïðè

ëþáîì

íåòðèâèàëüíîì

âàðüèðîâàíèè

q (t, α)

(∂q (t, α) /∂α 6= 0) ñ çàêðåïë¼ííûìè ãðàíè÷íûìè òî÷êàìè

¡

t

0

, q

0

¢

,

¡

t

1

, q

1

¢

â ðàñøèðåííîì êîîðäèíàòíîì ïðîñòðàí-

ñòâå äåéñòâèå ïî Ãàìèëüòîíó ïðèíèìàåò íà ïðÿìîì ïó-

òè ñòðîãèé ìèíèìóì.

Öåíòðàëüíàÿ îñü. Ñì. îñü âèíòà.
Öåíòðàëüíàÿ ñèëà. Ñì. ñèëà öåíòðàëüíàÿ.
Öåíòðàëüíîå ïîëå [1, ñ. 62], [37, ñ. 65]. Ñèëîâîå ïîëå, îá-

ðàçîâàííîå öåíòðàëüíûìè ñèëàìè.

Öåíòð

èíåðöèè

ñèñòåìû

ìàòåðèàëüíûõ

òî÷åê

[1, ñ. 73], [37, ñ. 50]. Ðàäèóñ-âåêòîð öåíòðà èíåðöèè

âû÷èñëÿåòñÿ ïî ôîðìóëå r

C

=

1

m

N

X

i=1

m

i

r

i

, m =

N

P

i=1

m

i

,

ãäå m

i

, r

i

ìàññà è ðàäèóñ-âåêòîð îòäåëüíîé òî÷êè.

Öåíòð êðèâèçíû [1, ñ. 17], [36, ñ. 7]. Öåíòð îêðóæíîñòè,

àïïðîêñèìèðóþùåé êðèâóþ â äàííîé òî÷êå.

Öåíòð ìàññ [1, ñ. 73], [37, ñ. 50]. Öåíòð èíåðöèè òâ¼ðäîãî

òåëà.

Öåíòðîáåæíûé

ìîìåíò

èíåðöèè

òâ¼ðäîãî

òåëà

[1, ñ. 180], [37, ñ. 93]. Âû÷èñëÿåòñÿ ïî ôîðìóëå
I

12

= I

21

=

P

i

m

i

x

i1

x

i2

, ãäå m

i

ìàññà òî÷êè íîìåð i,

x

i1

, x

i2

, x

i3

êîîðäèíàòû òî÷êè â îðòîíîðìèðîâàííîé

äåêàðòîâîé ñèñòåìå êîîðäèíàò. Àíàëîãè÷íî âû÷èñëÿþò-

ñÿ öåíòðîáåæíûå ìîìåíòû èíåðöèè I

13

= I

31

, I

23

= I

32

.

Öèêëè÷åñêàÿ êîîðäèíàòà [1, ñ. 277], [36, ñ. 139]. Êîîðäè-

íàòà q

k

íàçûâàåòñÿ öèêëè÷åñêîé, åñëè ôóíêöèÿ Ãàìèëü-

òîíà H (t, q

1

, . . . , q

k−1

, q

k+1

, . . . , q

n

, p

1

, . . . , p

n

)

îò íå¼ íå çà-

62

âèñèò. Öèêëè÷åñêàÿ êîîðäèíàòà q

k

ïîðîæäàåò ïåðâûé èí-

òåãðàë p

k

= c

ñîîòâåòñòâóþùåé ãàìèëüòîíîâîé ñèñòå-

ìû.

Öèêëè÷åñêàÿ ÷àñòîòà ãàðìîíè÷åñêîãî êîëåáàíèÿ. Ñì. êðó-

ãîâàÿ (óãëîâàÿ, öèêëè÷åñêàÿ) ÷àñòîòà ãàðìîíè÷åñêîãî êî-

ëåáàíèÿ.

Öèîëêîâñêîãî ôîðìóëà. Ñì. ôîðìóëà Öèîëêîâñêîãî.
×àñòîòà ãàðìîíè÷åñêîãî êîëåáàíèÿ [6, ÷. 1, ñ. 59],

[32, ñ. 849]. Âåëè÷èíà ν =

1

T

=

ω

2π

, îáðàòíàÿ ïåðèîäó T

ãàðìîíè÷åñêîãî êîëåáàíèÿ x = A sin (ωt + α).

×àñòîòà ãàðìîíè÷åñêîãî êîëåáàíèÿ êðóãîâàÿ (óãëîâàÿ,

öèêëè÷åñêàÿ). Ñì. êðóãîâàÿ (óãëîâàÿ, öèêëè÷åñêàÿ) ÷à-

ñòîòà ãàðìîíè÷åñêîãî êîëåáàíèÿ.

×àñòîòíûå õàðàêòåðèñòèêè [12, ñ. 45], [36, ñ. 128]. Ñî-

âîêóïíîñòü õàðàêòåðèñòèê: àìïëèòóäíî-ôàçîâàÿ, àìïëè-

òóäíàÿ, ôàçîâàÿ, äåéñòâèòåëüíàÿ, ìíèìàÿ.

×èñëî ñòåïåíåé ñâîáîäû ãîëîíîìíîé ñèñòåìû [1, ñ. 156],

[36, ñ. 23]. Êîëè÷åñòâî îáîáù¼ííûõ êîîðäèíàò.

×èñòîå

âðàùåíèå

òâ¼ðäîãî

òåëà

[22,

ñ.

50],

[37, ñ. 32]. Ïðè ÷èñòîì âðàùåíèè äëÿ íåêîòîðîé òî÷-

êè O òåëà âûïîëíÿåòñÿ V

O

= 0

, à äëÿ äðóãèõ òî÷åê B:

V

B

= [ω, ρ]

, ρ = OB.

Ýéëåðà äèíàìè÷åñêèå óðàâíåíèÿ. Ñì. äèíàìè÷åñêèå óðàâ-

íåíèÿ Ýéëåðà.

Ýéëåðà êèíåìàòè÷åñêèå óðàâíåíèÿ. Ñì. êèíåìàòè÷åñêèå

óðàâíåíèÿ Ýéëåðà.

Ýéëåðà ñëó÷àé. Ñì. ñëó÷àé Ýéëåðà.
Ýéëåðà óãëû. Ñì. óãëû Ýéëåðà.

63

Ýêâàòîðèàëüíàÿ ïëîñêîñòü [13, ñ. 88], [18, ñ. 257],

[37, ñ. 96]. Ïëîñêîñòü, ïåðïåíäèêóëÿðíàÿ â íåïîäâèæ-

íîé òî÷êå òâ¼ðäîãî òåëà îñè äèíàìè÷åñêîé ñèììåòðèè.

Ýêâàòîðèàëüíûé

ìîìåíò

èíåðöèè

[13,

ñ.

88],

[18, ñ. 257], [37, ñ. 96]. Ìîìåíò èíåðöèè îòíîñèòåëü-

íî îñè, ðàñïîëîæåííîé â ýêâàòîðèàëüíîé ïëîñêîñòè.

Ýêñöåíòðèñèòåò [1, ñ. 92], [37, ñ. 67]. Ïîñòîÿííàÿ e â ôîð-

ìóëå r =

p

1 + e cos (ϕ + β)

äëÿ îðáèò â ïîëå âñåìèðíîãî

òÿãîòåíèÿ êîíè÷åñêèõ ñå÷åíèé â ïîëÿðíûõ êîîðäèíà-

òàõ.

Ýëåêòðîìåõàíè÷åñêàÿ ñèñòåìà [8, ñ. 58], [20, ñ. 56],

[36, ñ. 69]. Ñèñòåìà, ñîñòîÿùàÿ èç âçàèìîäåéñòâóþùèõ

÷àñòåé: ìåõàíè÷åñêîé è ýëåêòðè÷åñêîé.

Ýëåêòðîìåõàíè÷åñêèå àíàëîãèè [8, ñ. 58], [20, ñ. 56],

[36, ñ. 66]. Ââåäåíèå äëÿ ýëåêòðè÷åñêîé öåïè: êèíåòè÷å-

ñêîé è ïîòåíöèàëüíîé ýíåðãèé, äèññèïàòèâíîé ôóíêöèè

Ðåëåÿ, îáîáù¼ííûõ ñèë, ñîîòâåòñòâóþùèõ íåïîòåíöè-

àëüíûì è íåäèññèïàòèâíûì ñèëàì. Íà îñíîâå ââåä¼ííûõ

ôóíêöèé âû÷èñëÿþòñÿ óðàâíåíèÿ Ëàãðàíæà óðàâíåíèÿ

ñîñòîÿíèÿ ýëåêòðè÷åñêîé öåïè.

Ýëåìåíòàðíàÿ ðàáîòà ñèë [1, ñ. 58], [36, ñ. 56]. Âû÷èñëÿ-

åòñÿ ïî ôîðìóëå δA =

N

P

i=1

(F

i

, dr

i

)

, ãäå F

i

ñèëà, dr

i

ïåðåìåùåíèå òî÷êè åå ïðèëîæåíèÿ.

Ýëåìåíòàðíàÿ

òåîðèÿ

ãèðîñêîïà

[1,

ñ.

209],

[36, ñ. 107]. Ïðåäïîëàãàåòñÿ, ÷òî óãëîâàÿ ñêîðîñòü ñîá-

ñòâåííîãî âðàùåíèÿ ω

1

çíà÷èòåëüíî ïðåâîñõîäèò óãëî-

âóþ ñêîðîñòü ïðåöåññèè ω

2

: ω

1

À ω

2

. Ýòî îáñòîÿòåëüñòâî

äà¼ò âîçìîæíîñòü ïîëüçîâàòüñÿ óïðîùåííîé ôîðìóëîé

äëÿ ìîìåíòà, ïîääåðæèâàþùåãî âûíóæäåííóþ ðåãóëÿð-

íóþ ïðåöåññèþ: M

O

= C [ω

2

, ω

1

]

.

64

Ýëëèïñîèä èíåðöèè [1, ñ. 182], [37, ñ. 94]. Íà îñè, ïðîõîäÿ-

ùåé ÷åðåç òî÷êó O òâ¼ðäîãî òåëà, îòêëàäûâàåòñÿ îòðå-
çîê OA = 1

.√

I

, ãäå I ìîìåíò èíåðöèè îòíîñèòåëüíî

äàííîé îñè. Ãåîìåòðè÷åñêîå ìåñòî òî÷åê A ýëëèïñîèä

èíåðöèè.

65

Ñïèñîê ëèòåðàòóðû

[1] Àéçåðìàí Ì.À. Êëàññè÷åñêàÿ ìåõàíèêà: Ó÷åáíîå ïîñîáèå.

3-å èçä. Ì.: Èçäàòåëüñòâî Ôèçèêî-ìàòåìàòè÷åñêîé ëè-

òåðàòóðû, 2005. 380 ñ.

[2] Aðíîëüä Â.È. Ìàòåìàòè÷åñêèå ìåòîäû êëàññè÷åñêîé ìåõà-

íèêè. Ì.: Íàóêà, 1974. 432 ñ.

[3] Àðíîëüä Â.È., Êîçëîâ Â.Â., Íåéøòàäò À.È. Ìàòåìàòè÷å-

ñêèå àñïåêòû êëàññè÷åñêîé è íåáåñíîé ìåõàíèêè. Èçä. 2-å,

ïåðåðàá. è äîï. Ì.: Åäèòîðèàë ÓÐÑÑ, 2002. 416 ñ.

[4] Áóñëàåâ Â.Ñ. Âàðèàöèîííîå èñ÷èñëåíèå: Ó÷åá. ïîñîáèå.

Ë.: Èçä-âî Ëåíèãð. óí-òà, 1980. 288 ñ.

[5] Áóòåíèí Í.Â., Ôóôàåâ Í.À. Ââåäåíèå â àíàëèòè÷åñêóþ

ìåõàíèêó. 2-å èçä., ïåð. è äîï. Ì.: Íàóêà, 1991.

256 ñ.

[6] Áóõãîëüö Í.Â. Îñíîâíîé êóðñ òåîðåòè÷åñêîé ìåõàíèêè. Â

2-õ ÷àñòÿõ. Ì.: Íàóêà, 1972.

[7] Ãàëèóëëèí À.Ñ. Àíàëèòè÷åñêàÿ ìåõàíèêà. Ì.: Âûñø.

øê., 1989, 264 ñ.

[8] Ãàíòìàõåð Ô.Ð. Ëåêöèè ïî àíàëèòè÷åñêîé ìåõàíèêè:

Ó÷åáíîå ïîñîáèå äëÿ âóçîâ / 3-å èçä. Ì.: ÔÈÇÌÀÒËÈÒ,

2001. 264 ñ.

[9] Ãîëäñòåéí Ã. Êëàññè÷åñêàÿ ìåõàíèêà. Íàóêà, 1975. 416 ñ.

[10] Ãîëóáåâ Þ.Ô. Îñíîâû òåîðåòè÷åñêîé ìåõàíèêè. Ó÷åáíèê.

Ì.: Èçä-âî ÌÃÓ. 1992. 525 ñ.

[11] Åãîðîâ À.È. Îáûêíîâåííûå äèôôåðåíöèàëüíûå óðàâíå-

íèÿ ñ ïðèëîæåíèÿìè. Ì.: ÔÈÇÌÀÒËÈÒ, 2003. 384 ñ.

[12] Åãîðîâ À.È. Îñíîâû òåîðèè óïðàâëåíèÿ. Ì.: ÔÈÇÌÀÒ-

ËÈÒ, 2004. 504 ñ.

[13] Æóðàâë¼â Â.Ô. Îñíîâû òåîðåòè÷åñêîé ìåõàíèêè. Èçä. 2-å

ïåðåðàá. Ì.: ÔÈÇÌÀÒËÈÒ, 2001. 320 ñ.

[14] Èáðàãèìîâ Í.Õ. Ãðóïïû ïðåîáðàçîâàíèé â ìàòåìàòè÷å-

ñêîé ôèçèêå. Ì.: Íàóêà, 1983. 280 ñ.

66

[15] Êèðÿêîâ Ï.Ï., Ñåíàøîâ Ñ.È., ßõíî À.Í. Ïðèëîæåíèå ñèì-

ìåòðèé è çàêîíîâ ñîõðàíåíèÿ ê ðåøåíèþ äèôåðåíöèàëü-

íûõ óðàâíåíèé. Èçäàòåëüñòâî ÑÎ ÐÀÍ, 2001. 192 ñ.

[16] Êîñìîíàâòèêà: Ýíöèêëîïåäèÿ / Ãë. ðåä. Â.Ï. Ãëóøêî

Ì.: Ñîâ. Ýíöèêëîïåäèÿ, 1985. 528 ñ.

[17] Ëèäîâ Ì.Ë. Êóðñ ëåêöèé ïî òåîðåòè÷åñêîé ìåõàíèêå.

Ì.: ÔÈÇÌÀÒËÈÒ, 2001. 478 ñ.

[18] Ëîéöÿíñêèé Ë.Ã., Ëóðüå À.È. Êóðñ òåîðåòè÷åñêîé ìåõàíè-

êè. Òîì II. Ì.: ÃÈÒÒË, 1955. 596 ñ.

[19] Ëóðüå À.È. Àíàëèòè÷åñêàÿ ìåõàíèêà. Ì.: Ôèçìàòãèç,

1961. 824 ñ.

[20] Ëüâîâè÷ À.Þ. Îñíîâû òåîðèè ýëåêòðîìåõàíè÷åñêèõ ñè-

ñòåì. Èçä.-âî Ëåíèíãð. óí-òà, 1973. 196 ñ.

[21] Ìàãíóñ Ê. Ãèðîñêîï. Òåîðèÿ è ïðèìåíåíèå. Ì.: Ìèð, 1974.

528 ñ.

[22] Ìàðêååâ À.Ï. Òåîðåòè÷åñêàÿ ìåõàíèêà: Ó÷åáíèê äëÿ óíè-

âåðñèòåòîâ. Èæåâñê: ÍÈÖ Ðåãóëÿðíàÿ è õàîòè÷åñêàÿ

äèíàìèêà, 2001. 572 ñ.

[23] Ìàòåìàòè÷åñêàÿ ýíöèêëîïåäèÿ. Ì.: ÑÝ.  5 ò., 1977-1985.

1152 ñ.; 1104 ñ.; 1184 ñ.; 1216 ñ.; 1248 ñ.

[24] Îëâåð Ï. Ïðèëîæåíèå ãðóïï Ëè ê äèôôåðåíöèàëüíûì

óðàâíåíèÿì. Ïåð. ñ àíãë. Ì.: Ìèð, 1989. 639 ñ.

[25] Ïàðñ Ë.À. Àíàëèòè÷åñêàÿ äèíàìèêà: Ïåð. ñ àíãë. Ì.:

Íàóêà, 1971. 636 ñ.

[26] Ïåòêåâè÷ Â.Â. Òåîðåòè÷åñêàÿ ìåõàíèêà: Ó÷åáíîå ïîñîáèå.

Íàóêà. Ôèçìàòëèò, 1981. 496 ñ.

[27] Ïóàíêàðå À. Èçáðàííûå òðóäû â òðåõ òîìàõ. Òîì II. Èçä-

âî Íàóêà, 1974. 1000 c.

[28] Ðóø Í., Àáåòñ Ï., Ëàëóà Ì. Ïðÿìîé ìåòîä Ëÿïóíîâà â

òåîðèè óñòîé÷èâîñòè. Ì.: Ìèð, 1980. 304 ñ.

[29] Ñáîðíèê òåðìèíîâ ïî êëàññè÷åñêîé ìåõàíèêå íà ïÿòè ÿçû-

êàõ: ðóññêèé, íåìåöêèé, àíãëèéñêèé, ôðàíöóçñêèé, ïîëü-

ñêèé. Wydavnictwa Naukowo-Techniczne, Warszawa, 1965.

67

[30] Ñóñëîâ Ã.Ê. Òåîðåòè÷åñêàÿ ìåõàíèêà. 3-å èçä. Ì.: Ë.:

Ãîñòåõèçäàò, 1946. 655 ñ.

[31] Òåîðåòè÷åñêàÿ ìåõàíèêà. Òåðìèíîëîãèÿ. Áóêâåííûå îáî-

çíà÷åíèÿ âåëè÷èí: Ñáîðíèê ðåêîìåíäóåìûõ òåðìèíîâ. Ì.:

Íàóêà, 1984. Âûï. 102.

[32] Ôèçè÷åñêèé ýíöèêëîïåäè÷åñêèé ñëîâàðü. Ì.: Ñîâ. ýí-

öèêëîïåäèÿ, 1984. 944 ñ.

[33] ×åëíîêîâ Þ.Í. Êâàòåðíèîííûå è áèêâàòåðíèîííûå ìîäå-

ëè è ìåòîäû ìåõàíèêè òâåðäîãî òåëà è èõ ïðèëîæåíèÿ.

Ãåîìåòðèÿ è êèíåìàòèêà äâèæåíèÿ. Ì.: ÔÈÇÌÀÒËÈÒ,

2006. 512 ñ.

[34] ×åòàåâ Í.Ã. Òåîðåòè÷åñêàÿ ìåõàíèêà / Ïîä ðåä. Â.Â. Ðó-

ìÿíöåâà, Ê.Å. ßêèìîâîé. Ì.: Íàóêà, 1987. 368 ñ.

[35] Ýíöèêëîïåäèÿ äëÿ äåòåé. Òîì 14. Òåõíèêà / Ãëàâ. ðåä.

Ì.Ä. Àêñåíîâà. Ì.: Àâàíòà

+

, 2000. 688 c.

[36] ßêîâåíêî Ã.Í. Êðàòêèé êóðñ àíàëèòè÷åñêîé äèíàìèêè

Ì.: ÁÈÍÎÌ. Ëàáîðàòîðèÿ çíàíèé, 2004. 238 ñ.

[37] ßêîâåíêî Ã.Í. Êðàòêèé êóðñ òåîðåòè÷åñêîé ìåõàíèêè

Ì.: ÁÈÍÎÌ. Ëàáîðàòîðèÿ çíàíèé, 2006. 116 ñ.

[38] Hughes Peter C. Spacecraft attitude dynamics. Dover

publications, inc. Mineola, New York, 2004. 574 p.

68