Piotr Łukowski, Wykład dla studentów prawa

Logiczne podstawy prawoznawstwa

Piotr Łukowski

1

Piotr Łukowski, Wykład dla studentów prawa

WYKŁAD 13

przykłady odpowiedzi na

możliwe pytania egzaminacyjne

2

Piotr Łukowski, Wykład dla studentów prawa

☺

Uwaga: na egzaminie mogą pojawić się pytania nie uwzględnione w przedstawionych niżej przykładach.

3

Piotr Łukowski, Wykład dla studentów prawa

ZADANIE 1

1. Podaj definicję wyrażeń:

„metajęzyk języka L”, „język przedmiotowy”, „język drugiego stopnia”.

2. Podaj przykład zdania w języku przedmiotowym, zdania w języku drugiego stopnia i w języku

trzeciego stopnia.

3. Jakim językiem jest metajęzyk dla języka piątego stopnia?

ODPOWIEDŹ

ad 1.

- Metajęzykiem języka L jest taki język L’, w którym wypowiadamy się o wyrażeniach języka L.

- Językiem przedmiotowym jest język, w którym wypowiadamy się o rzeczywistości nas

otaczającej (pozajęzykowej).

- Językiem drugiego stopnia jest język, w którym wypowiadamy się o wypowiedziach

formułowanych w języku pierwszego stopnia.

ad 2.

Przykład zdania w języku przedmiotowym: „Słońce świeci”.

Przykład zdania w języku drugiego stopnia: „„Słońce świeci” jest zdaniem fałszywym”.

Przykład zdania w języku trzeciego stopnia: „„„Słońce świeci” jest zdaniem fałszywym” jest

zdaniem języka polskiego”.

ad 3.

Metajęzykiem języka piątego stopnia jest język szóstego stopnia.

4

Piotr Łukowski, Wykład dla studentów prawa

ZADANIE 2

Jaki jest warunek zrozumiałego dla obu stron posługiwania się w rozmowie wyrażeniem W?

Odpowiedź zilustruj przykładami.

ODPOWIEDŹ

Tym warunkiem jest tożsamość rozumienia wyrażenia W przez obie strony rozmowy. Chodzi tu

między innymi o:

- tożsamość tego do czego W się odnosi (obiektu, stanu rzeczy).

Przykład: Błędem jest, gdy jedna strona pojmuje W = „reformę systemu karania” jako złagodzenie

kar, a strona druga jako racjonalizację karania.

- tożsamość metody rozstrzygania o poprawności użycia W.

Przykład: Błędem jest, gdy jedna strona rozumie udowodnienie tezy jako rozumowania opartego na

związku tetycznym, a strona druga na związku logicznym.

- tożsamości funkcji użycia W.

Przykład: Błędem jest, gdy jedna strona rozumie wypowiedź jako poważną, a strona druga uważa ją

za żart - różne rozumienie siły illokucyjnej.

- zgodność zabarwienia emocjonalnego towarzyszącego użyciu W.

Przykład: Błędem jest, gdy jedna strona rozumie W jako zjawisko pozytywne, więc pożądane, a

strona druga jako zjawisko neutralne, więc obojętne.

5

Piotr Łukowski, Wykład dla studentów prawa

ZADANIE 3

Jakie znasz kryteria prawdy? Podaj policyjno-sądowe przykłady zastosowania każdego z nich.

ODPOWIEDŹ

Kryterium klasyczne - prawdziwym jest sąd zgodny z rzeczywistością.

Przykład: Odrzucamy twierdzenie, że A popełnił samobójstwo, ponieważ strzał pozbawiający A życia padł z odległości 10 m.

K. koherencyjne - prawdziwym jest sąd zgodny (spójny, niesprzeczny) z innymi sądami.

Przykład: W wyniku konfrontacji dwóch sprzecznych ze sobą zeznań, akceptujemy zeznania A jako spójne ( A sobie w nich nie zaprzeczył) i odrzucamy zeznania B jako niespójne ( B sobie w nich zaprzeczył).

K. oczywistości ( intuicyjne) - prawdziwym jest sąd, który wydaje się być oczywistym.

Przykład: „ A musiał rozpoznać B, bo był od niego oddalony o 3 m, na otwartej przestrzeni, w samo południe.”

K. strukturalne ( formalno-logiczne) - prawdziwość sądu wynika z budowy składniowej zdania go wyrażającego, może też być wypadkową prawdziwości i fałszywości innych sądów.

Przykład: „Raz z pana zeznań wynika, że był pan na miejscu zbrodni, innym zaś razem wynika, że nie.

Proszę się zdecydować! Przypominam, że zeznaje pan pod przysięgą!”

K. autorytetu - prawdziwym jest sąd wypowiedziany przez kogoś obdarzonego autorytetem lub przez znawcę

tematu (prestiżowy ośrodek naukowy, ekspert z danej dziedziny, wiarygodna gazeta/stacja tv).

Przykład: Każda ekspertyza jest tu przykładem.

K. zgody powszechnej - prawdziwym jest sąd podzielany przez większość ludzi.

Przykład: „Przecież wszyscy świadkowie mówią to samo!”

K. pragmatyczne - prawdziwym jest sąd, który jest pożyteczny.

Przykład: Umorzono śledztwo w sprawie Kuby Rozpruwacza, aby nie wywołać pogromu śydów w Londynie

(przypuszczenie podane w filmie produkcji BBC wyemitowanym przez Discovery Channel).

6

Piotr Łukowski, Wykład dla studentów prawa

ZADANIE 4

Kiedy kryterium K jest warunkiem koniecznym, a kiedy wystarczającym zajścia zdarzenia

opisanego zdaniem A? Rozpoznaj, które kryterium w podanym przykładzie jest warunkiem

koniecznym, a które wystarczającym dla zdania „ Ulice są mokre”?

Przykład: Ulice są mokre wtedy i tylko wtedy gdy pada deszcz lub jeździła polewaczka.

ODPOWIEDŹ

K jest warunkiem wystarczającym (dostatecznym) zajścia A, jeśli zajście K pociąga za sobą zajście A: ∀ x ( K( x) → A( x))

K jest warunkiem koniecznym zajścia A, jeśli z faktu, iż zaszło A wynika, że zaszło K:

∀ x ( A( x) → K( x))

W podanym przykładzie:

♠ warunkiem koniecznym dla zdania „ Ulice są mokre” jest alternatywa „ Pada deszcz lub jeździła

polewaczka”, bo „ Jeśli ulice są mokre, to pada deszcz lub jeździła polewaczka”.

♠ warunkiem wystarczającym jest każde z trzech zdań: „ Pada deszcz lub jeździła polewaczka”,

„ Pada deszcz”, „ Jeździła polewaczka”, bo:

1. „ Jeśli pada deszcz lub jeździła polewaczka, to ulice są mokre”;

2. „ Jeśli pada deszcz, to pada deszcz lub jeździła polewaczka” (prawo logiczne) i

„ Jeśli pada deszcz lub jeździła polewaczka, to ulice są mokre” (założenie), więc

„ Jeśli pada deszcz, to ulice są mokre” (prawo przechodniości);

3. „ Jeśli jeździła polewaczka, to pada deszcz lub jeździła polewaczka” (prawo logiczne) i

„ Jeśli pada deszcz lub jeździła polewaczka, to ulice są mokre” (założenie), więc

„ Jeśli jeździła polewaczka, to ulice są mokre” (prawo przechodniości).

7

Piotr Łukowski, Wykład dla studentów prawa

ZADANIE 5

Czym jest zbiór w sensie dystrybutywnym, a czym zbiór w sensie kolektywnym? Który zbiór jest

dystrybutywny, a który kolektywny: 1. ręka złożona z barku, ramienia, przedramienia, dłoni; oraz

2. klasa 3b rozumiana jako zbiór uczniów ją stanowiących. Czym różni się relacja należenia

dystrybutywnego od relacji należenia kolektywnego?

ODPOWIEDŹ

Zbiór w sensie dystrybutywnym jest przedmiotem abstrakcyjnym, ujmującym w całość różne,

częstokroć nie związane ze sobą obiekty. Zbiór dystrybutywny nie jest obiektem ani czasowym,

ani przestrzennym.

Zbiór w sensie kolektywnym (mereologicznym), to obiekt przestrzenny (bryła, płaszczyzna lub

linia), którego elementami są jego części. Istnieje w czasie i przestrzeni.

Przykład:

1. Ręka złożona z barku, ramienia, przedramienia, dłoni, to zbiór w sensie kolektywnym.

2. Kasa 3b rozumiana jako zbiór uczniów ją stanowiących, to zbiór w sensie dystrybutywnym.

Relacja należenia dystrybutywnego jest przeciwzwrotna i przeciwprzechodnia, bo: a) żaden zbiór

do siebie nie należy oraz b) uczeń należący do klasy 3b, która należy do zbioru klas szkoły nr 65, sam nie jest elementem zbioru klas szkoły nr 65.

Relacja należenia kolektywnego jest zwrotna i przechodnia, bo: a) każdy zbiór jest własnym

elementem (jest ingrediensem) oraz b) palec będący częścią dłoni, która jest częścią ręki, sam

też jest częścią ręki.

8

Piotr Łukowski, Wykład dla studentów prawa

ZADANIE 6

Co to jest absurd, a co nonsens? Podaj przykład absurdu i przykład nonsensu.

ODPOWIEDŹ

Absurd to zdanie, z którego wynika sprzeczność, czyli koniunkcja dwóch zdań, z których jedno

jest zaprzeczeniem drugiego.

Przykład: Kupiłem wczoraj rybę drugiej świeżości.

Skoro ryba była drugiej świeżości, to znaczy że jednocześnie była świeża i nieświeża. Bo

świeżość jest jedna - pierwsza i zarazem ostatnia - jak twierdzi Woland z Mistrza i Małgorzaty.

Nonsens to wyrażenie, które nie posiada znaczenia.

Przykład: Człowiek jest ssakiem parzystym. Człowiek to zwierzą podzielne przez 5.

Człowiek jest ssakiem non-parzystym (bo przecież ani parzystym, ani nieparzystym).

9

Piotr Łukowski, Wykład dla studentów prawa

ZADANIE 7

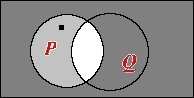
Stosująca diagramy Venna sprawdź, czy ze zdań „ Każdy człowiek jest łapówkarzem” i „ Każdy

jest człowiekiem” wynika na mocy rachunku nazw Arystotelesa zdanie „ Każdy jest łapówkarzem”.

Oceń poprawność tego wnioskowania.

ODPOWIEDŹ

Rozumowanie to reprezentuje schemat: ∀ x ( P( x) → Q( x)) → (∀ x P( x) → ∀ x Q( x)), gdzie P( x) oznacza „ x jest człowiekiem”, Q( x) oznacza „ x jest łapówkarzem”. Ograniczmy rozumowanie do dziedziny, którą stanowi zbiór wszystkich ludzi.

1.

2.

Dowód nie wprost - zakładam prawdziwość obu przesłanek: ∀ x ( P( x) → Q( x)) i ∀ x P( x), oraz fałszywość wniosku ∀ x Q( x). Mamy wówczas dwa przypadki, tak jak na rysunkach. W obu

dochodzimy do sprzeczności - nie może bowiem być tak, aby coś należało do zbioru pustego.

Rozumowanie jest niepoprawne, gdyż chociaż poprawne formalnie nie jest ono poprawne

materialnie, z powodu fałszywości pierwszej przesłanki - przecież nie wszyscy ludzie są

łapówkarzami. Gdyby dziedziną nie był zbiór ludzi, to fałszywą byłaby także druga przesłanka.

[komentarz: skąd więc ten głupi, a popularny w Polsce tekst „ U nas wszyscy biorą”?]

10

Piotr Łukowski, Wykład dla studentów prawa

ZADANIE 8

Co to jest rozumowanie? Rozpoznaj rodzaj rozumowania w podanym przypadku. Wiem, że Jan

się wzbogacił. Na tej podstawie sądzę, że Jan wziął łapówkę.

Co w tym rozumowaniu jest w racją, a co następstwem? Czy jest ono niezawodne?

Rozpoznaj związek jaki zachodzi między racją i następstwem, który jest podstawą tego

rozumowania.

ODPOWIEDŹ

Rozumowanie to myślenie uzasadniające, w którym przyjmujemy określone wartości pewnych

zdań i dochodzimy do przeświadczenia o określonych wartościach logicznych innych zdań.

Przyjmuję prawdziwość następującej implikacji: Jeśli Jan wziął łapówkę, to Jan się wzbogacił.

Zatem, racją jest „ Jan wziął łapówkę”, a następstwem „ Jan się wzbogacił”.

Podane jako przykład rozumowanie jest tłumaczeniem, czyli dobieraniem racji do znanego

skądinąd jako prawdziwe następstwa.

Tłumaczenie jest rozumowaniem zawodnym, gdyż prawdziwość następnika implikacji nie

gwarantuje prawdziwości jej poprzednika.

Podane jako przykład rozumowanie opiera się na związku przyczynowo-skutkowym wyrażonym

implikacją: „ Jeśli Jan wziął łapówkę, to Jan się wzbogacił”.

Uwaga na marginesie (ostrzeżenie):

Racja „ Jan wziął łapówkę” to przyczyna, a następstwo „ Jan się wzbogacił” to skutek.

11

Piotr Łukowski, Wykład dla studentów prawa

ZADANIE 9

Co to jest rozumowanie? Rozpoznaj rodzaj rozumowania w podanym przypadku. Wiem, że Jan

kupił dom. Na tej podstawie sądzę, że Jan się wzbogacił.

Co w tym rozumowaniu jest w racją, a co następstwem? Czy jest ono niezawodne?

Rozpoznaj związek jaki zachodzi między racją i następstwem, który jest podstawą tego

rozumowania.

ODPOWIEDŹ

Rozumowanie to myślenie uzasadniające, w którym przyjmujemy określone wartości pewnych

zdań i dochodzimy do przeświadczenia o określonych wartościach logicznych innych zdań.

Przyjmuję prawdziwość następującej implikacji: Jeśli Jan kupił dom, to Jan się wzbogacił.

Zatem, racją jest „ Jan kupił dom”, a następstwem „ Jan się wzbogacił”.

Podane jako przykład rozumowanie jest wnioskowaniem, czyli dobieraniem następstwa do znanej

skądinąd jako prawdziwa racji.

Wnioskowanie jest rozumowaniem niezawodnym, gdyż prawdziwość poprzednika implikacji

gwarantuje prawdziwość jej następnika.

Podane jako przykład rozumowanie opiera się na związku strukturalnym (ew. przyczynowo-

skutkowym) wyrażonym implikacją: „ Jeśli Jan kupił dom, to Jan się wzbogacił”.

Uwaga na marginesie (ostrzeżenie):

Racja „ Jan kupił dom” to skutek, a następstwo „ Jan się wzbogacił” to przyczyna.

12

Piotr Łukowski, Wykład dla studentów prawa

ZADANIE 10

Co to jest nazwa? Jaka nazwa jest pustą, a jaka sprzeczną? Czym jest zakres nazwy pustej?

Podaj przykład nazwy sprzecznej oraz nazwy pustej niesprzecznej. Określ w jakim stosunku ze

względu na zakres pozostają nazwy, które podałeś jako przykład. W jakim stosunku pozostają

nazwy „nazwa pusta” i „nazwa sprzeczna”?

ODPOWIEDŹ

Nazwa jest to wyrażenie mogące wystąpić w zdaniu jako podmiot lub orzecznik orzeczenia

imiennego. Orzeczenie imienne to orzeczenie stwierdzające o podmiocie, że jest taki a taki.

Zatem, jeśli mamy zdanie „a jest b”, to a jest w tym zdaniu podmiotem, a b orzecznikiem

orzeczenia imiennego.

Nazwa pusta to nazwa, która nie ma desygnatu. Zatem zakresem nazwy pustej jest zbiór pusty.

Nazwa sprzeczna to taka nazwa, dla której założenie istnienia desygnatu prowadzi do

sprzeczności, czyli do koniunkcji dwóch zdań, z których jedno jest zaprzeczeniem drugiego.

Przykładem nazwy sprzecznej jest „parterowy wieżowiec”. Przykładem nazwy pustej

niesprzecznej jest „stupiętrowy dom w Poznaniu”. Desygnat nazwy sprzecznej nie może istnieć

więc nie istnieje, zaś desygnat nazwy sprzecznej nie istnieje choć może istnieć. Zakresem każdej

z tych dwóch nazw jest zbiór pusty. Ponieważ istnieje tylko jeden zbiór pusty, zatem nazwy te są

równozakresowe - mają ten sam zakres.

„Nazwa pusta” jest nazwą nadrzędną (ze względu na zakres) wobec nazwy „nazwa sprzeczna”,

ponieważ każda nazwa sprzeczna jest pusta, ale nie każda nazwa pusta jest sprzeczna.

13

Piotr Łukowski, Wykład dla studentów prawa

Inne możliwe zadania egzaminacyjne:

- Czym jest rozumowanie przez analogię? Podaj przykład trafnego i nietrafnego zastosowania

analogii.

- Jakie znasz błędy definiowania? Podaj przykład każdego z nich. Kiedy błąd definiowania jest

błędem logicznym? Który z błędów definiowania nie jest błędem logicznym?

- Jak ocenisz następujące rozumowanie: "Kto ukończył 18 lat życia, ten może sam kupić

samochód. Kto może sam kupić samochód, ten ma pieniądze na kupno samochodu. Zatem, kto

ukończył 18 lat życia, ten ma pieniądze na kupno samochodu."?

- Kiedy zdanie W wynika ze zdania Z? Jakie znasz związki wynikania? Podaj przykład każdego z

nich. Jak jest różnica między wynikaniem a opartym na nim rozumowaniem?

- Omów wieloznaczność, nieostrość i ogólność nazwy. Podaj przykłady nazwy: wieloznacznej,

nieostrej, ogólnej.

- Co to jest indukcja? Wymień kanony Milla. Omów kanon jedynej zgodności. Podaj przykład

trafnego i nietrafnego zastosowania tego kanonu.

- Co to jest relacja określona na zbiorze Z? Jaka relacja jest relacją równoważnościową na

zbiorze Z? Co to jest klasa abstrakcji relacji równoważności? Podaj przykład relacji

równoważnościowej i podziału dokonanego przy jej użyciu.

- Podaj definicję kłamstwa.

14