Egzamin dla Aktuariuszy z 17 marca 2008 r.
Matematyka Finansowa
Zadanie 1
,
0 055
1
i =
; v =
2
1 + i
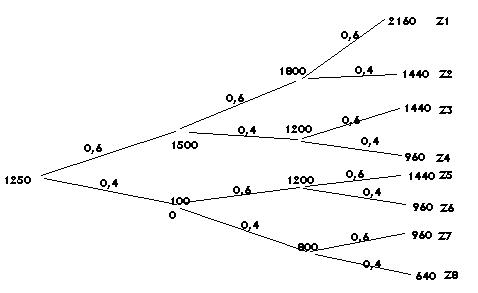
K – ile wydamy na obligację z tytułu długiej pozycji K = 1500(
2
3
4
5
6
v + v + v + v + v + v ) 6
+ 50000 v
3000( 5
,
0
2
v + v + 5
,
1
3
v + 2 4
v )+ (200000 − 2 K ) 4
ODP =
v ≈
3000(
2
3
4
v + v + v + v ) 8
,
1 5
+ 1
( 00000 − K ) 4
v
Zadanie 2
1000 ⋅ ,
1 01
1
968
= 968 →
=
= v
1
1 + r
1 + r
1000 ⋅ ,
1 01
1
1
1000 ⋅ ,
1 01⋅ ,
1 011
1
937
(
= 937 →
=
= v
1 + r 1 + r
1 + r 1 + r
1000 ⋅ ,
1 01⋅ ,
1 011
1 )(
2 )
( 1)(
)
2
2
1000 ⋅ ,
1 01⋅ ,
1 011⋅ ,
1 012
1
907
(
→
=
= v
1 + r 1 + r 1 + r 1 + r 1 + r 1 + r 1000 ⋅ ,
1 01⋅ ,
1 011⋅ ,
1 012
1 )(
2 )(
3 )
( 1)( 2)(
)
3
3
é 0
,
0 5 + 5
,
0 ⋅ ,
0 2
0
,
0 5 + 5
,
0 ⋅ ,
0 2
0
,
0 5 + 5
,
0 ⋅ ,
0 2 + 1 ù
Z 1 = ê
+
+
ú
ë
1 + r
+ r
+ r
+ r
+ r
+ r
1
(1 1)(1 2 ) (1 1)(1 2 )( 3) 1000000
1
û
Z 2 = 1000000 (
[ 0,
0 5 + 5
,
0 ⋅ ,
0 2) v + ( 0
,
0 5 + 5
,
0 ⋅ ,
0 )
2 v + ( 0
,
0 5 + )
1 v
1
2
3 ]
Z 3 = 100000 [
0 ( 0
,
0 5 + 5
,
0 ⋅ ,
0 )
2 v + 0
,
0 5 v + ( 0
,
0 5 + 5
,
0 ⋅ ,
0 2 + )
1 v
1
2
3 ]
Z 4 = 100000 [
0 ( 0
,
0 5 + 5
,
0 ⋅ ,
0 )
2 v + 0
,
0 5 v + ( 0
,
0 5 + )
1 v
1
2
3 ]
Z 5 = 100000 [
0
0
,
0 5 v + ( 0
,
0 5 + 5
,
0 ⋅ ,
0 )
2 v + ( 0
,
0 5 + 5
,
0 ⋅ ,
0 2 + )
1 v
1
2
3 ]
Z 6 = 100000 [
0
0
,
0 5 v + ( 0
,
0 5 + 5
,
0 ⋅ ,
0 )
2 v + ( 0
,
0 5 + )
1 v
1
2
3 ]
Z 7 = 100000 [
0
0
,
0 5 v + 0
,
0 5 v + ( 0
,
0 5 + 5
,
0 ⋅ ,
0 2 + )
1 v
1
2
3 ]
0
0
,
0 5 v + 0
,
0 5 v + ( 0
,
0 5 + )
1 v
1
2
3 ]
i wychodzi odpowiedź (A)
Zadanie 3
Trzeba znaleźć rozkład A,B,A+B
A: X - wypłata
A
P( X
A = 10000) =
9
,
0 5
P( X
P X
A = 7000) =
( A = 6000) = 0,
0 5 ⋅ 5
,
0
= 0
,
0 25
rozkład A:
æ
1 ö
æ
10
ö
Pç A = ÷ = Pç A =
−1÷ = 9
,
0 5
è
9 ø
è
9
ø
æ
3 ö
æ
2 ö
Pç A = − ÷ = ,
0 025 = Pç A = − ÷
è
9 ø
è
9 ø
B: P( X
B = 10000) =
9
,
0 5
P( X
B = 6200) =
0
,
0 25
P( X
B = 6800) =
0
,
0 25
æ
1 ö
Pç B = ÷ = 9
,
0 5
è
9 ø
æ
28 ö
æ
22 ö
Pç B = −
÷ = Pç B = −
÷ = ,
0 025
è
90 ø
è
90 ø
A+B: ozn: a – bankructwo A, b – bankructwo B
P(a)=P(b)=0,05
P( a ∩ b) = 0
P( a′ ∩ b′) = P( a b)′
∪
= 1− P( a ∪ b) = 1− P( a) − P( b) + P( a ∩ b) = 1− , 0 05 ⋅ 2 = 9
,
0
P( a′ ∩ b) = P (Ω − a)∩ b) = P (
[ Ω ∩ b)− ( a ∩ b)]= P( b) − P( a ∩ b) = 0, 0 5
P( b′ ∩ a) = P (Ω − b) ∩ a) = P (
[ Ω ∩ a)− ( b ∩ a)]= P( a) − P( a ∩ b) = 0, 0 5
P( X
A+ B = 20000) =
9
,
0
P( X
A+ B = 16000) =
0
,
0 5 ⋅ 5
,
0
P( X
A+ B = 17000) =
0
,
0 5 ⋅ 5
,
0
P( X
P X
A+ B = 16200) =
( A+ B =16800) = 0,
0 25
æ
1 ö
Pç A + B = ÷ = 9
,
0
è
9 ø
æ
1 ö
æ
1 ö
æ
18 ö
æ
12 ö
Pç A + B = − ÷ = Pç A + B = −
÷ = Pç A + B = −
÷ = Pç A + B = −
÷ = ,
0 025
è
9 ø
è
18 ø
è
180 ø
è
180 ø
ì
14
3
0 x ≤ -
ï
0 x ≤ −
ï
45
ï
9
ï
æ 14
11 ù
ï
æ
ï
3
2 ù
,
0 02
5 x ∈ ç -
;−
ï ,
0 02
5 x ∈ ç - ;− ú
ïï
ú
è 45 45û
P( A < x) = í è 9 9û
P( B < x) = í ï
ï
æ 11 5 ù
ï
æ 2 1ù
,
0 0
5 x ∈ ç -
;
,
0 0
5 x ∈ ç − ;
ï
ú
è 45 45û
ï
ú
è 9 9û
ï
ï
5
î
ï
1 x > 1
ï
1 x >
î
45
ì
20
ï
0 x ≤ -
ï
180
ï
æ 20
18 ù
ï ,
0 02
5 x ∈ ç −
;−
ú
ï
è 180 180û
ï
æ 18
12 ù
,
0 0
5 x ∈ ç −
;−
ïï
ú
è 180 180û
P( A + B < x) = í ï
æ 12
10 ù
ï ,
0 07
5 x ∈ ç −
;−
ú
è 180 180û
ïï
æ 10 20 ù
ï
1
,
0 x ∈ ç −
;
ú
ï
è 180 180û
ï
20
ï
1 x >
î
180
2
40
3
60
VaR
( )
A =
=
VaR
( )
A =
=
%
5
2, %
5
9
180
9
180
11
44
14
56
VaR
( B) =
=
VaR
( B) =
=
%
5
2, %
5
45
180
45
180
18
20
VaR
( A + B) =
VaR
( A + B) =
%
5
2, %
5
180
180
sprawdzamy i wychodzi odpowiedź C
Zadanie 4
Chcemy by kwota, którą dostaniemy po 3 miesiącach była niezaleŜna od X – cena akcji Z opcji kupna max(X-40;0)
Z opcji sprzedaŜy max(40-X;0)
k
- ilość opcji kupna
1
k
- ilość opcji sprzedaŜy
2
c – kwota na inwestycję wolną od ryzyka X – tyle musimy zwrócić (z krótkiej sprzedaŜy) Dostaniemy: k max( X − 40 0
; ) + k max 4
( 0 − X 0
; )
0,025
+ ce
− X > 0 (chcemy Ŝeby taka
1
2
nierówność zachodziła)
Dla X>40 k ( X − 40) 0,025
+ ce
− X > 0 → k = 1
1
1
Dla X<40 k (40 − X ) 0,025
+ ce
− X > 0 → k = 1
−
2
2
k ⋅ 3 + k ⋅ ,
2 25 + c = 42 → 3 − ,
2 25 =
7
,
0 5 → c = 42 − 7
,
0 5 = 4 ,
1 25
1
2
0,025
ce
− 40 = 4 ,125 0,025
e
− 40
ODP = (4 ,
1 25 0,025
e
− 40) −0,025
e
≈ ,
2 24
Zadanie 5
r - stopa realna
0
r – stopa nominalna
f – stopa inflacji
1 + r
1 + r
0 = 1+ f
r =0,0455
0
1+r=x
1+r=1,0455(1+f)
y=1+f
70
60
50
−130 +
+
+
= 1
,
9
1 + r
1
( + r)2
1
( + r)3
−130 3
x + 70 2
x + 60 x + 50 = 1
,
9
3
x ⋅10
1391 3
x − 700 2
x − 600 x − 500 = 0
f ( y) = 1391⋅ ,
1 04553 3
y − 700 ⋅ ,
1 04552 2
y − 600 ⋅ ,
1 0455 y − 500 = 0
i sprawdzamy które najbliŜej:
dla y=1,08 czyli f=8% f(y) równa się około –67,46
dla f=9% około –34,19
dla f=10% około 6,22
dla f=11% około 34,99
dla f=12% około ....
czyli C najbliŜej
Zadanie 6
Model CAPM: r − r = β r − r i
f
i ( M
f )
r
f =
,
0 06
dla I: β =
;
8
,
0
r
r
r
r
M −
f =
,
0 04
1 l
u
b M − f = ,
0 041 + ,
0 023
r =
0
,
0 6 + 8
,
0 ⋅ 0
,
0 41 =
0
,
0 92
8 l
u
b r =
0
,
0 6 +
+
=
1
1
(8
,
0
0
,
0 41
0
,
0 2 )
3
1
,
0 112
dla II: β = 9
,
0
;
7 r =
0
,
0 6 + 9
,
0 7 ⋅ 0
,
0 41 =
0
,
0 9977
2
Zadanie 7
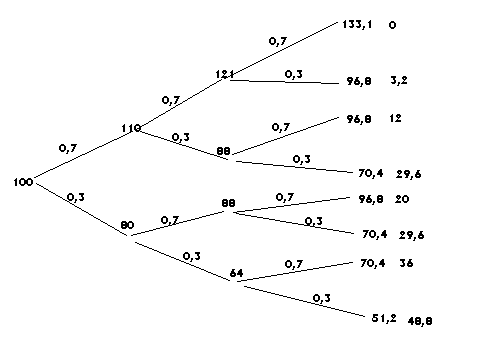
ODP = ( ,
3 2 ⋅
2
,
0 7
3
,
0 + 12 ⋅
2
,
0 7
3
,
0 + 2 ,
9 6 ⋅
2
3
,
0
,
0 7 + 20 ⋅
2
,
0 7
3
,
0 + 2 ,
9 6 ⋅
2
3
,
0
,
0 7 + 36 ⋅
2
3
,
0
,
0 7 + 48 8
, ⋅
3 ) 1
3
,
0
3
,
1 08
= [ ,3
( 2 + 12 + 20) ,
0 72 3
,
0 + (2 ,
9 6 + 2 ,
9 6 + 36) 3
,
0 2 ,
0 7 + 48 8
,
3
⋅
] 1
3
,
0
≈ 9
,
9
,
1 083
Zadanie 8
∞
2
å k (− )1 k vk
1
k 1
ODP = =
g
dzi
e v =
∞
0
,
1 5
å k(− )1 k vk
k 1
=
− v + 22 2
v − 32 3
v + 42 4
v + ...
=
− v + 2 2
v − 3 3
v + 4 4
v ....
L = 22 v 2 + 42 v 4 + 62 v 6 + ... − v + 32 v 3 + 52 v 5 + ...
1
4
4
4
4
2
4
4
4
4
3
(
)
1
4
4
4
2
4
4
4
3
A
B
M = 2 v 2 + 4 v 4 + 6 v 6 + ... − v + v 3 3 + v
5 5 + ...
1
4
4
4
2
4
4
4
3
(
)
1
4
4
4
2
4
4
4
3
C
D
2
Av = 22 4
v + 42 6
v + 62 8
v + ...
( A 1− 2 v)= 22 2 v +(42 −22) 4 v +(62 −42) 6 v +...= 2 n −( n− )22 = 4 n−4 =
= (4 ⋅ 2 − 4) 2
v + (4 ⋅ 4 − 4) 4
v + ... = 4(2 2
v + 4 4
v + .. ).− 4( 2
4
v + v + .. ).
2
3
Bv = v + 32 5
v + 52 7
v + ...
B(1− 2
v ) = v + (32 − )
1 3
v + (52 − 32 ) 5
v + ... = v + (4 ⋅ 3 − 4) 3
v + (4 ⋅ 5 − 4) 5
v + ... =
= v + 4(3 3
v + 5 5
v + .. ).− 4( 3
5
v + v + .. ).
X
Y
6
4
4
7
4
4
8
6
4
4
7
4
4
8
2
4
4 2 v + 4 v + .. ).− ( 2
4
4 v + v + .. ).− v − 4( 3
5
3 v + 5 v + .. ).+ ( 3
5
4 v + v + .. ).
L =
2
1 − v
2
Xv = 2 4
v + 4 6
v + ...
X (
2
v
v
1 − v )
2
2
2
4
2
2
= 2 v + 2 v + ... =
→ X =
2
1 − v
(1− v )22
2
Yv = 3 5
v + 5 7
v + ...
5
3
2 v
+ −
Y (
3 v
2
v
1 − v )
5
2
3
5
7
3
2
1
= 3 v + 2 v + 2 v + ... = 3
v
v +
→ Y =
2
2
1 − v
1 − v
5
3
2 v
+
2
2
3 v
3
2
8 v
4 v
4 v
−
(
1
−
− v − 4
v
+
2
1 − v )2
2
2
2
1 − v
1 − v
1 − v
L =
2
1 − v
2
Cv = 2 4
v + 4 6
v + ...
C(
2
v
v
1 − v )
2
2
2
4
2
2
= 2 v + 2 v + ... =
→ C =
2
1 − v
(1− v )22
2
3
Dv = v + 3 5
v + 5 7
v + ...
D(
2
v
v
v
1 − v )
3
3
3
5
2
2
= v + 2 v + 2 v + ... = v +
→ D =
+
2
2
1 − v
1 − v
(1− v )22
M=C-D
= L
ODP
≈ ,
0 025
M
Zadanie 9
Źle sformułowane zadanie – nie wiadomo o co chodzi Moim zdaniem chodzi o zmianę róŜnicy cen opcji Czyli korzystając z pu-call parity róŜnica C-P nie zaleŜy od zmienności czyli jak była taka jest i stąd ODP D jest prawidłowa
Zadanie 10
−
−
−
1 æ 3 + 2 2,5
e
3 − 3 2,5
e
ö 6
2,5
− e
P( h) =
+
=
çç
÷÷
2
5
5
10
è
ø
−
−
−
1 æ 2 − 2 2,5
e
2 + 3 2,5
e
ö 4
2,5
+ e
P( b) =
+
=
çç
÷÷
2
5
5
10
è
ø
ODP = P( h) ⋅100 0,025 0 1, e
e
+ P( b 1
) 00 0,025 0,025
e
e
≈ 110