Uniwersytet Śląski

Wydział Informatyki i Nauki o Materiałach

Sprawozdanie na potrzeby przedmiotu

Analiza i złożoność obliczeniowa algorytmów

Zadanie 39. Wyszukiwanie

Michał Daniel

Magisterskie, zaoczne, grupa F

Sosnowiec 2012

1. Treść zadania

Niech A będzie posortowaną tablicą n różnych liczb całkowitych, wśród których mogą być też

liczby ujemne. Zaprojektuj efektywny algorytm znajdowania indeksu k, 1 ≤ k ≤ n, takiego, że A[k]

= k, o ile taki indeks istnieje. Następnie dokonaj analizy zaprojektowanego algorytmu (wyznacz

optymistyczny i pesymistyczny czas jego działania).

2. Teoria

Jedno z założeń zadania mówi, iż A jest posortowaną tablicą zawierającą różne liczby całkowite,

w tym również liczby ujemne. Założenie to umożliwia zastosowanie bisekcji znanej z algorytmu

wyszukiwania binarnego. Ponieważ zbiór A jest posortowany i zawiera różne elementy, możemy

wyznaczyć jego środkowy element, sprawdzić jego wartość i porównać ją z jego indeksem. Jeśli te

wartości są równe to otrzymujemy rozwiązanie zadania w jego optymistycznym czasie działania.

Jeśli natomiast wartości te są różne, to sprawdzając czy wartość tego elementu jest większa lub

mniejsza od swojego indeksu możemy wybrać połówkę zbioru w którym należy spodziewać się

rozwiązania (i tym samym zmniejszyć obszar poszukiwań o połowę). Nowo otrzymaną połówkę

zbioru również możemy podzielić na pół i tym samym wykonać operację wyszukiwania od nowa na

zbiorze mniejszym o połowę. Operację taką należy wykonywać dopóki nie odnaleźliśmy

rozwiązania lub ilość elementów w zbiorze jest większa niż 1 (czyli dopóty dopóki podział jest

możliwy).

Dodatkowym warunkiem jaki możemy zastosować w algorytmie jest warunek sprawdzenia, czy

wartość skrajnie prawego elementu zbioru (tzn o indeksie końca przedziału) nie jest mniejsza od 1.

Jeśli jest, oznacza to, że w zadanej tablicy nie odnajdziemy rozwiązania, ponieważ tablica jest

posortowana.

3. Rozwiązanie

Algorytm zapisany w pseudokodzie:

Binarysearch(A)

1

lewo := 0

2

prawo := n-1

3

while lewo <= prawo do

4

if A[prawo] < 1 then return false

5

środek := (lewo + prawo)/2

6

if środek = A[środek] then return środek

7

if A[środek] > środek then prawo := środek – 1

8

else lewo := środek + 1

9

return false

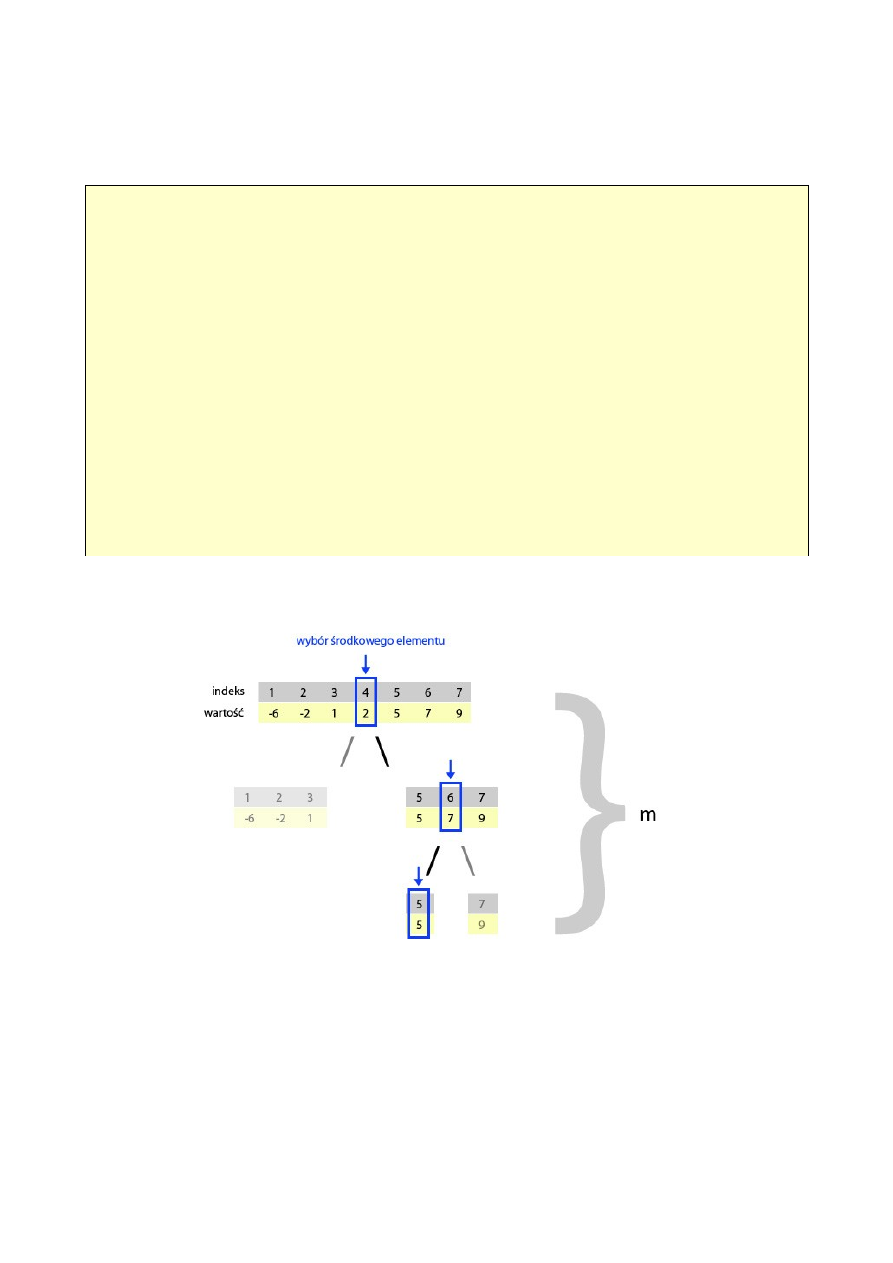
Graficzne przedstawienie działania algorytmu dla A = [-6, -2, 1, 2, 5, 7, 10]

Złożoność optymistyczna

Optymistyczny czas działania powyższego algorytmu wynosi 1 operację, ponieważ pierwszy

element, który wybierzemy jako środkowy w zadanym zbiorze może spełniać A[k] = k lub też

ostatni element zbioru A[n] może być niedodatni. W takim przypadku algorytm wykona 1

porównanie.

Złożoność pesymistyczna

Pesymistyczny przypadek to taki, dla którego rozwiązanie nie istnieje, a wszystkie elementy

zbioru są dodatnie. Jak możemy zaobserwować na powyższym rysunku, zbiór który należy

przeszukać z każdym przebiegiem zmniejsza się o połowę. Ponieważ w każdym przebiegu pętli

możemy wykonać maksymalnie 3 porównania możemy określić, że liczba wykonywanych operacji

x wynosi:

gdzie m to liczba podziałów zbioru. Liczba operacji porównania jest w tym przypadku pomijalna,

ponieważ nie ma znaczącego wpływu (jest to stała), tak więc:

A więc pesymistyczna złożoność obliczeniowa algorytmu jest klasy O(log n).

Załącznik 1 – implementacja algorytmu w PHP

Algorytm zapisany w języku PHP wraz z objaśnieniami:

// parametrem jest posortowana tablica
function binarysearch(&$array)
{

if (!is_array($array)) return false;

$l = 0; // indeks początku przedziału
$p = count($array)-1; // indeks końca przedziału

while ($l <= $p) // główna pętla algorytmu
{

// jeśli wartość skrajnie prawego elementu jest ujemna = brak rozwiązania

if ($array[$p] < 1) {
return false;
}

$s = floor(($l+$p)/2); // znajdujemy środek przedziału
$value = $array[$s]; // pobieramy wartość środkowego elementu

if ($s == $value) { // jeśli wartość i indeks są takie same, mamy rozwiązanie
return $s;
}

// jeśli wartość elementu jest większa niż indeks to idziemy
// do lewej połówki – tylko tam możemy znaleźć rozwiązanie

if ($value > $s) $p = $s - 1;
else $l = $s + 1; // w przeciwnym wypadku do prawej

}
return false; // brak rozwiązania

}