Guitar Music Theory Norm Vincent Lydian Dominant Theory

Lydian-Dominant Theory

for

Improvisation

Norm Vincent

Lydian-Dominant Music Theory assumes the 12-Tone Tempered Scale
and the naturally occurring Physics of the OverTone Series. A small
amount of high school level Algebra is used in this treatise as Music
Theory is highly Mathematical. In fact, in Plato's Scheme of things,
Mathematics is derived from Music! Music (i.e. organized vibrational
frequencies) is Primal. This sounds like modern physics to me.

Although one does not have to be a Mathematical Wizard to do Music,
exciting new research has shown a definite link between the two. Musical
Performance involves very high-level integrated mental processes we have
only begun to explore in a Scientific manner. I find it regrettable that
knowledge known to ancient peoples has become lost, suppressed, and
distorted. It is my intention that this treatise be a "first step" toward the
development of a truly scientific exploration of the Domain of Music and all
its ramifications. We will start with the basic physical facts.

The OverTone Series

The OverTone Series is a naturally occurring physically demonstrable set of
Frequencies present above any given pitch. The relative mix of these upper
frequencies is different for every tone generator. This is why different
musical instruments sound remarkably different even though they are
sounding the same pitch. The OverTone Series is infinite in extent, but in
practice, only the first few are important to us here as the relative volume of
the upper partials gradually becomes inaudible.

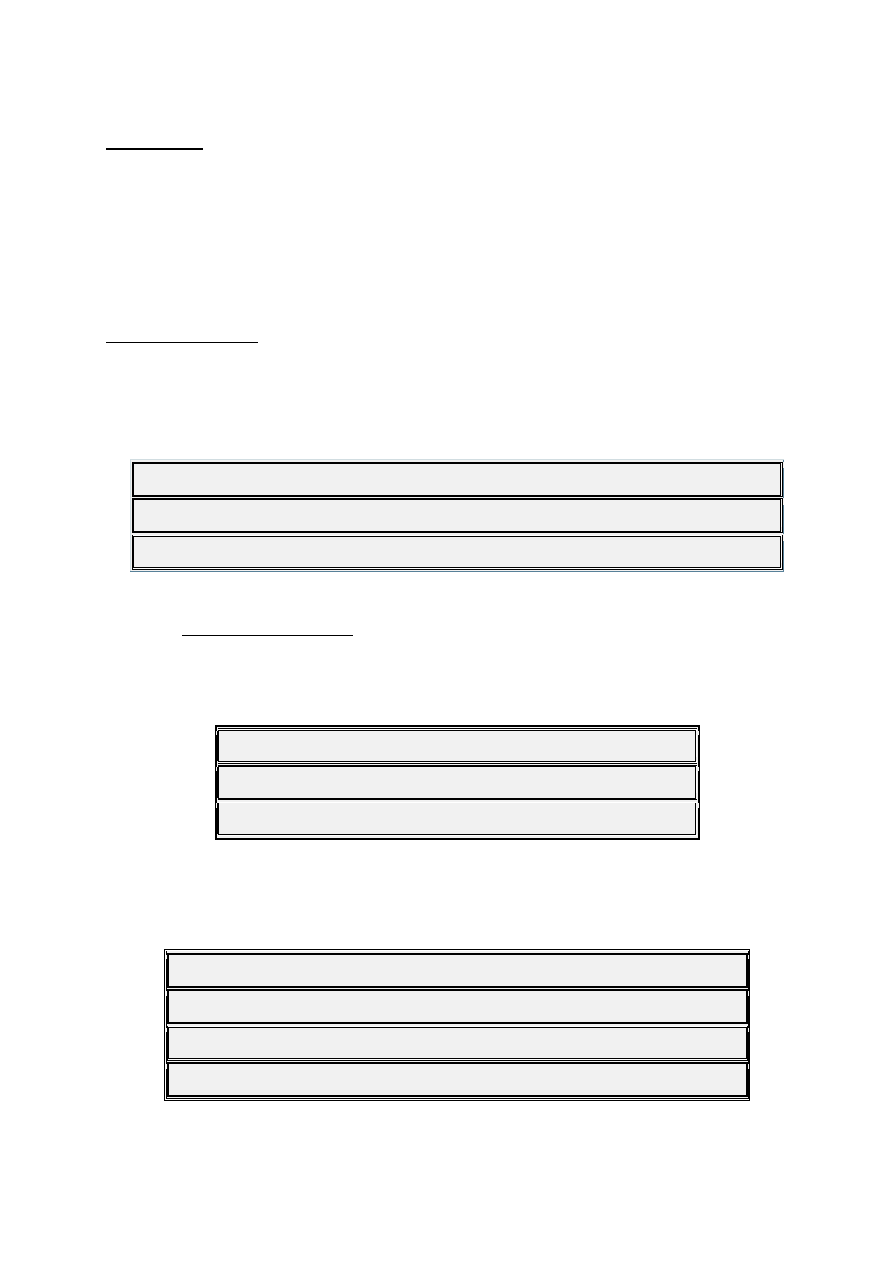
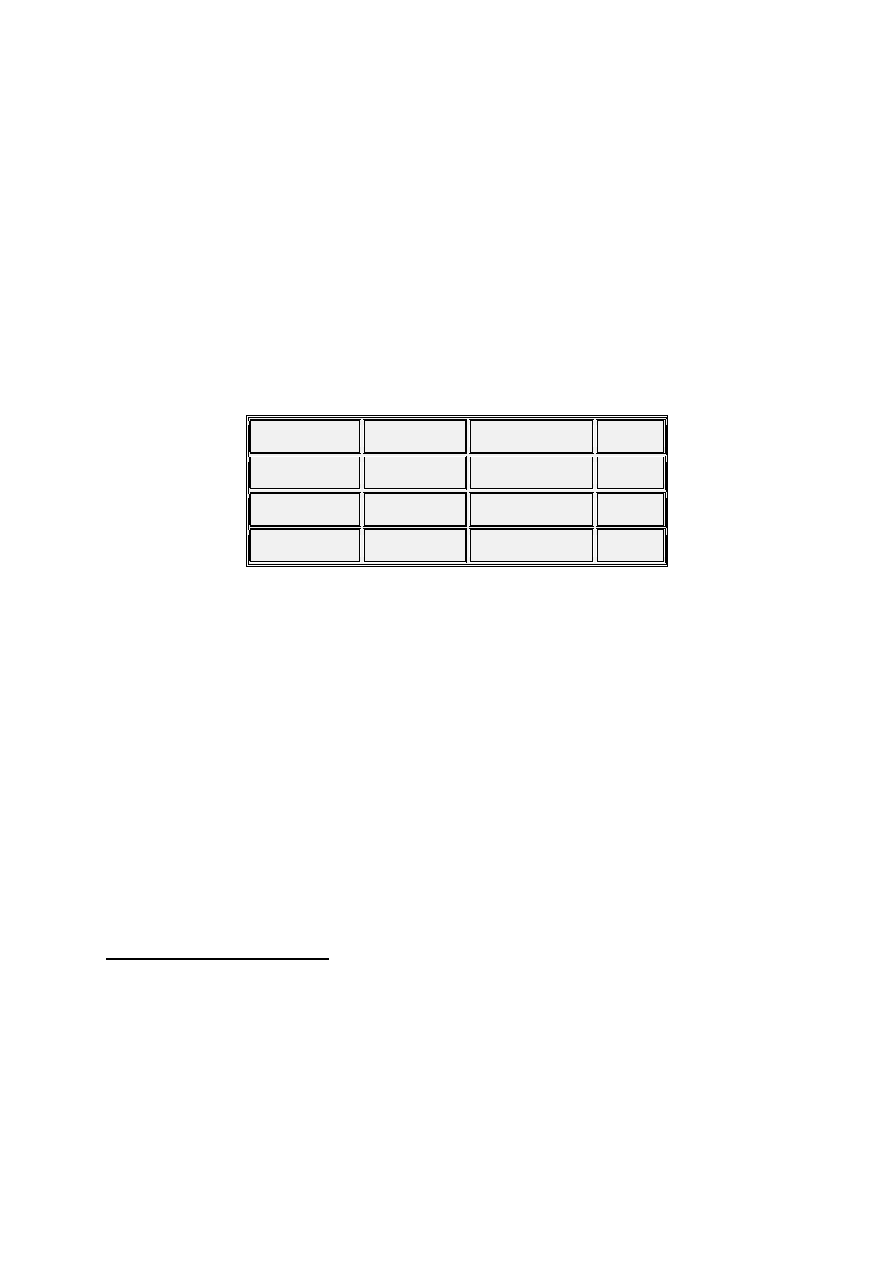
OverTone #

1 - 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 ...

Note #

1 - 1 5 1 3 5

7 1 2 3

4 5 6

7 7 1 ...

Note Name

C - C G C E G B

C D E F

G A B

B C ...

Try this experiment on a Piano. Hold Down the Sustain Pedal. Strongly Hit
and Release a low 'C'. What do you hear? I hear all sorts of other strings
vibrating. The sounding strings are not accidental, they are strictly
determined by the OverTone Series. These associated frequencies are called
Harmonics.

The exact single-octave Harmonic Series values are given in the next
table. It is an ordering of the Rational Numbers. These values are used the
same way the fundamental values of Sines and Cosines are used in
Trigonometry. You simply multiply the initial pitch by these values to
derive the frequency of the desired harmonic.

OverTone # 1 - 2 3

4 5

8 9

10 11

12 13

14 15

16 ...

Note #

1 - 1 5

1 3

7 1 2

7 7

1 ...

Harmonic # 1 - 1 3/2 1 5/4 3/2 7/4 1 9/8 5/4 11/8 3/2 13/8 7/4 15/8 1 ...

A few comments on the OverTone Series relevant to Lydian-Dominant
Theory. Notice the natural occurrence of the

7 and the

11. Also notice the

natural occurrence of the Chord » {1 3 5

7} and the Scale » {1 2 3

4 5 6

7 1}. I will refer back to these facts later on in this treatise. The OverTone

Series is explained in greater depth in my book Natural Music Theory.

The 12-Tone Tempered System

Our modern 12-Tone Tempered Scale is derived from the Pythagorean
Spiral of 5

ths

.The 12-Tone Tempered Scale approximates the values of

the Pure Harmonics of the naturally occurring OverTone Series using
only the ratio for the 5

» (3/2).

What is a 5

? Briefly, what is known as a 5

is the first distinct (other than

octave doublings) OverTone to emerge from the OverTone Series and is
associated with the number 3. Experiments on strings by ancient people
showed that when you take a string tuned to any starting pitch and divide it
into 2

you get octave doublings. When you divide it into 3

, you get what is

known as a perfect 5

. When you divide it into 5

, you get what is known as

a Major 3

. When you divide it into 7

, you get what is known as a Minor 7

This process can continue to any desired level and is explained in greater
depth in my book Natural Music Theory.

The formula for the Pythagorean Spiral of 5

ths

is:

p·(3/2)

k is any Integer and p is any starting Pitch.

Twelve intervals of a 5

almost closes in on itself - the "snake almost

swallows its tail". The discrepancy has been known about since ancient times
and goes by various names. I call it - the Pythagorean Error Factor.
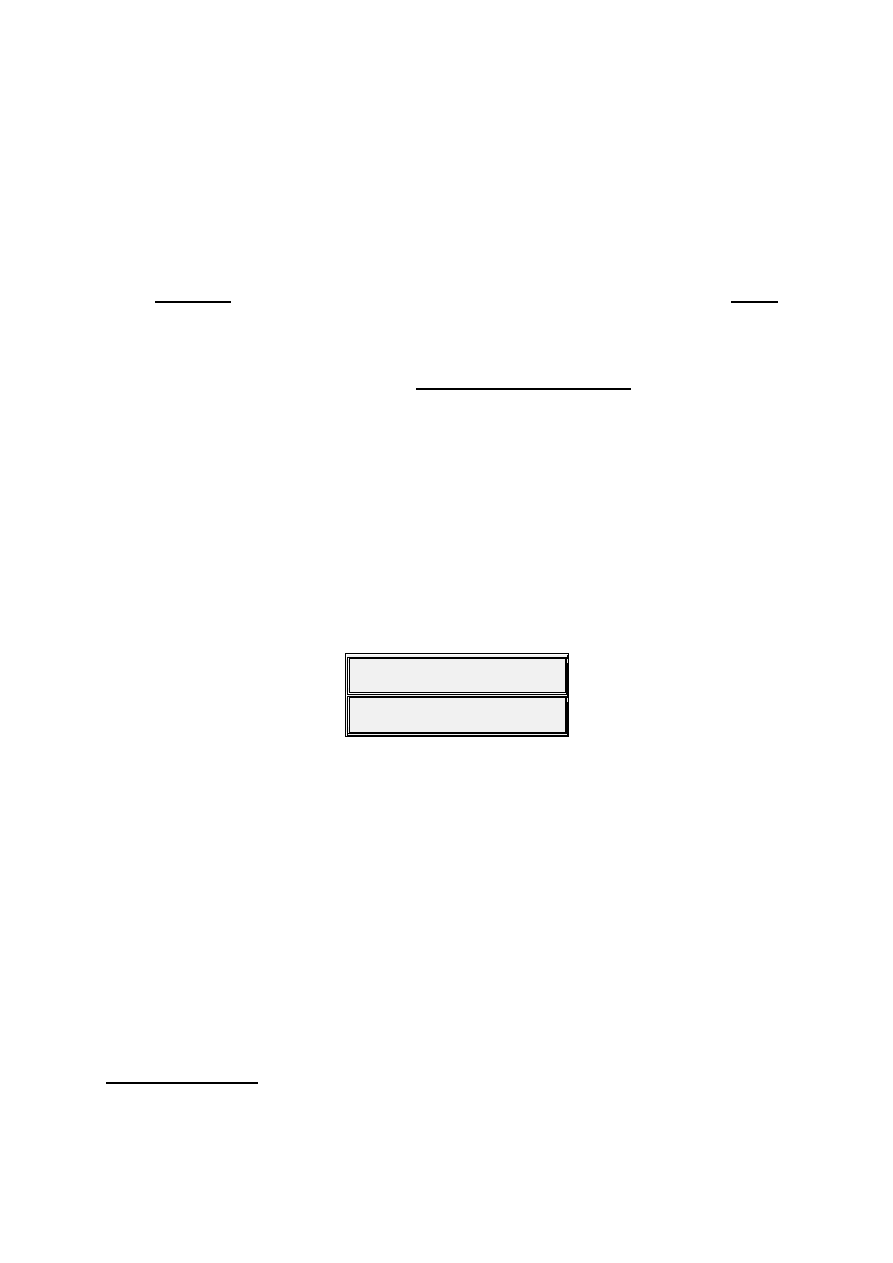
Consider the following table consisting of Twelve 5

ths

(#)

and Twelve 5

ths

Down

(b)

C G

C F

In natural occurring pure intervallic evolutions, a B

in not equivalent to a

C. Likewise, a D

is not equivalent to a C. Both B

and D

are audibly

different from C. However, it was discovered in early classical times
(European) that if you take an almost imperceptible amount (2 cents) away
from each 5

, you can get a Cycle of 5

ths

that does close in on itself

perfectly. The "snake eats its tail". Bach's Well Tempered Clavier was a great
success in promoting the new system. The gain is tremendous - we now
have 12 different Keys to modulate to that all sound remarkably good. The
cost is that each 5

is 2 cents flat, a price that most are willing to pay for

the usefulness of the system. In the 12-Tone Tempered system B

=C.

Thus we end up with a true Pythagorean Cycle of 5

ths

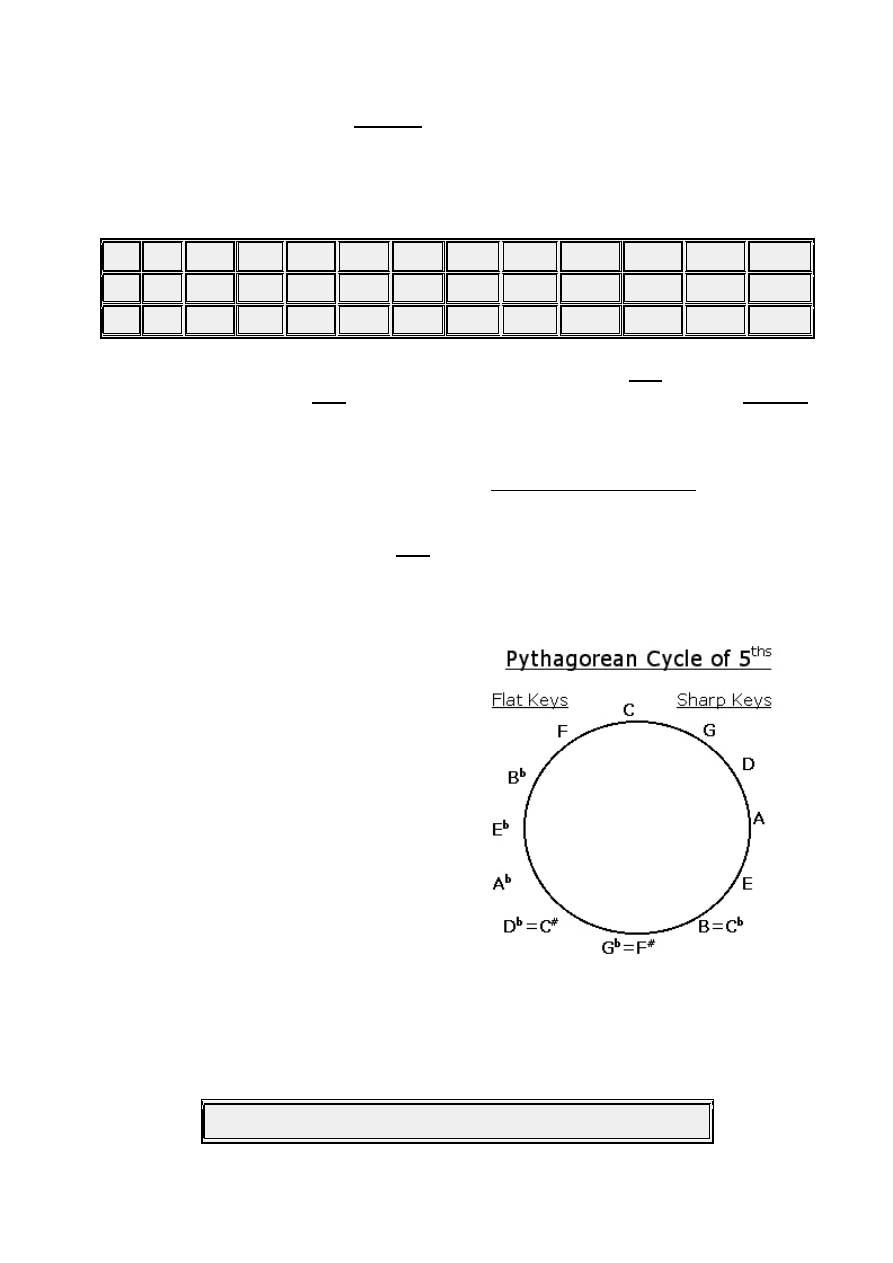
To the right is a table showing this
Cycle that is very concise and
informative. From it we can clearly
see each of the 15 Standard Keys
and their relationships to each other.
The Dominant relationship goes
counter-clockwise. Notice the
enharmonic keys. This is where the
Flat Keys merge into the Sharp Keys
due to Tempering.

From this information we can
construct what is known as the
Chromatic Scale This Scale contains
12 exactly equal intervals of a semi-
tone (1/2 step).

{ C=B

, C

, D, D

, E=F

F=E

, F

, G, G

, A, A

, B=C

}

The exponential formula for our 12-Tone Tempered System is:

p·2

(k/12)

k is any Integer and p is any starting Pitch.

Why is the number 2 in this formula? Because the result multiplying or
dividing any frequency by 2 is an 'octave' higher or lower. The Psycho-
Acoustical perception of the same/different quality of octaves is
discussed in great depth in my book Natural Music Theory.

The value of a chromatic interval is p·2

(1/12)

. The accepted Modern Standard

is A=440 cps, but any base pitch will do. In fact, the base pitch has been
steadily rising. It was A=432 in Beethoven's time.

The 12-Tone Tempered System is not without its problems. As opposed to
the fact that 5

ths

and 4

ths

are only slightly out of tune, other intervals are

grossly distorted. In particular, the out-of-tune-ness of the Major 3

led to

what is known as Just Intonation - the harmonic value (5/4) being used
rather than the Pythagorean (81/64). Similar problems exist with the

4, and other theoretically important notes.

The Cosmic Quirk involving the number 12, legendary for its number
mystic properties, in evolving our common 12-Tone Tempered System and
the evolution of other N-Tone Tempered Systems from Cycles different from
(3/2), some of which are more exact than the 12-Tone Tempered, are
developed in great detail in my book Natural Music Theory.

Discussion of Dominance in Music

Before we go any further, I will define Lydian-Dominant. Lydian is a word
found in old Greek treatises on Music referring to the classical 7-note (so-
called Dia-Tonic) Scale with the 4

Scale degree raised (#) a half-step. The

easy way to remember this is by playing a Scale on a Piano starting on 'F'
and pressing only the white notes. As the 4

degree of an F-Major Scale is a

, we clearly have a different Scale - the Lydian Scale. This Scale is a

Major Scale with a

degree. In the exposition that follows, I will be doing

all examples in the Key of C. The C

Lydian

Scale is spelled: { C D E F

G A B

C }.

The notion of Dominance is quite complex. Western polyphonic Multi-Keyed
Music based on the 12-Tone Tempered Scale has led to the concept of the
Dominant 7

Chord. It is a psycho-acoustic tension and release

phenomenon. This is how it is postulated to work in the European Classical
Music Theory.

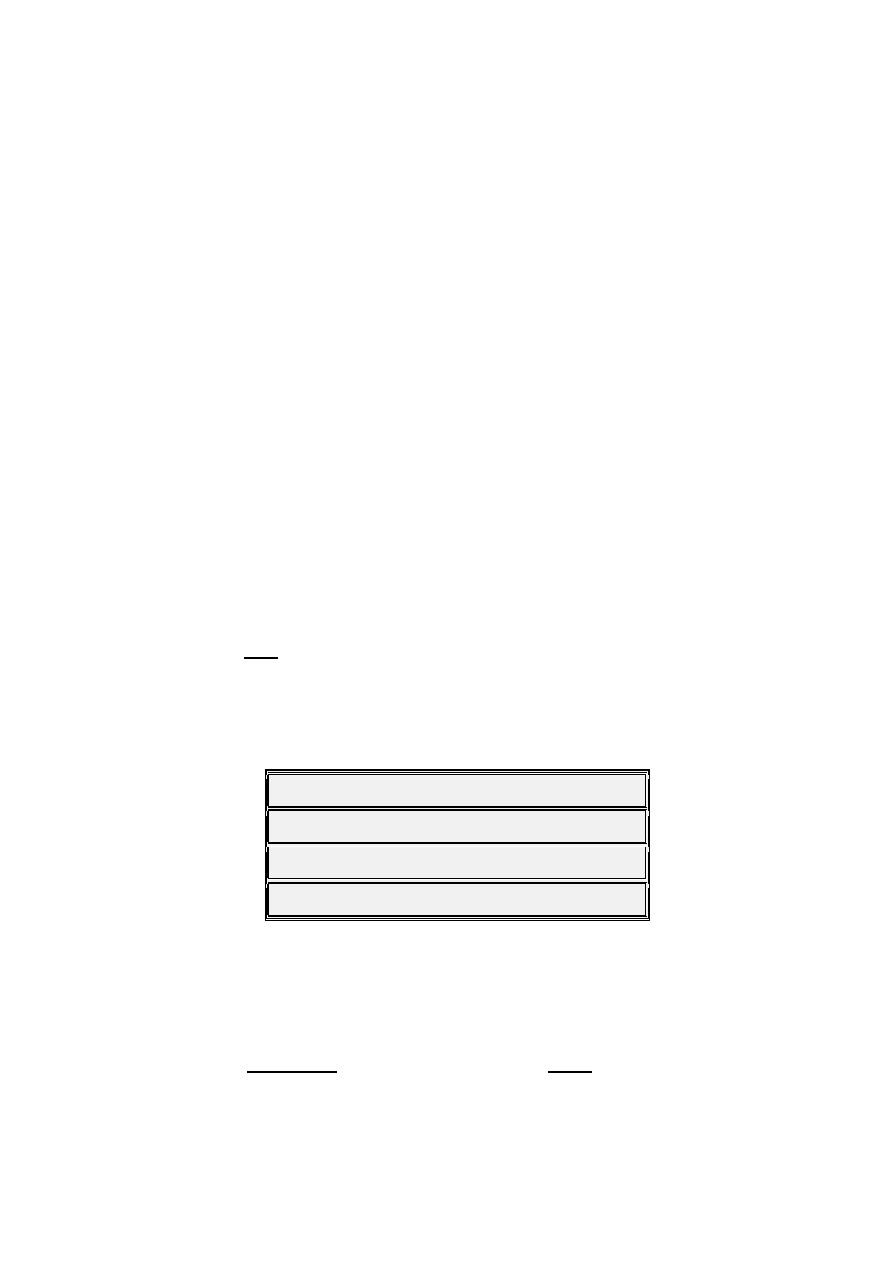
The four note Chord formed on the 5

degree of the Major Scale is called

the Dominant 7

Chord. It is formally referred to as the

Chord. The

presence of the Dominant 7

(

7) in the Chord sets up a tension that needs

to be released. Classical theory states that this tension is released by
resolving to the Key Root Chord, also known as the

Chord - G

»»» C.

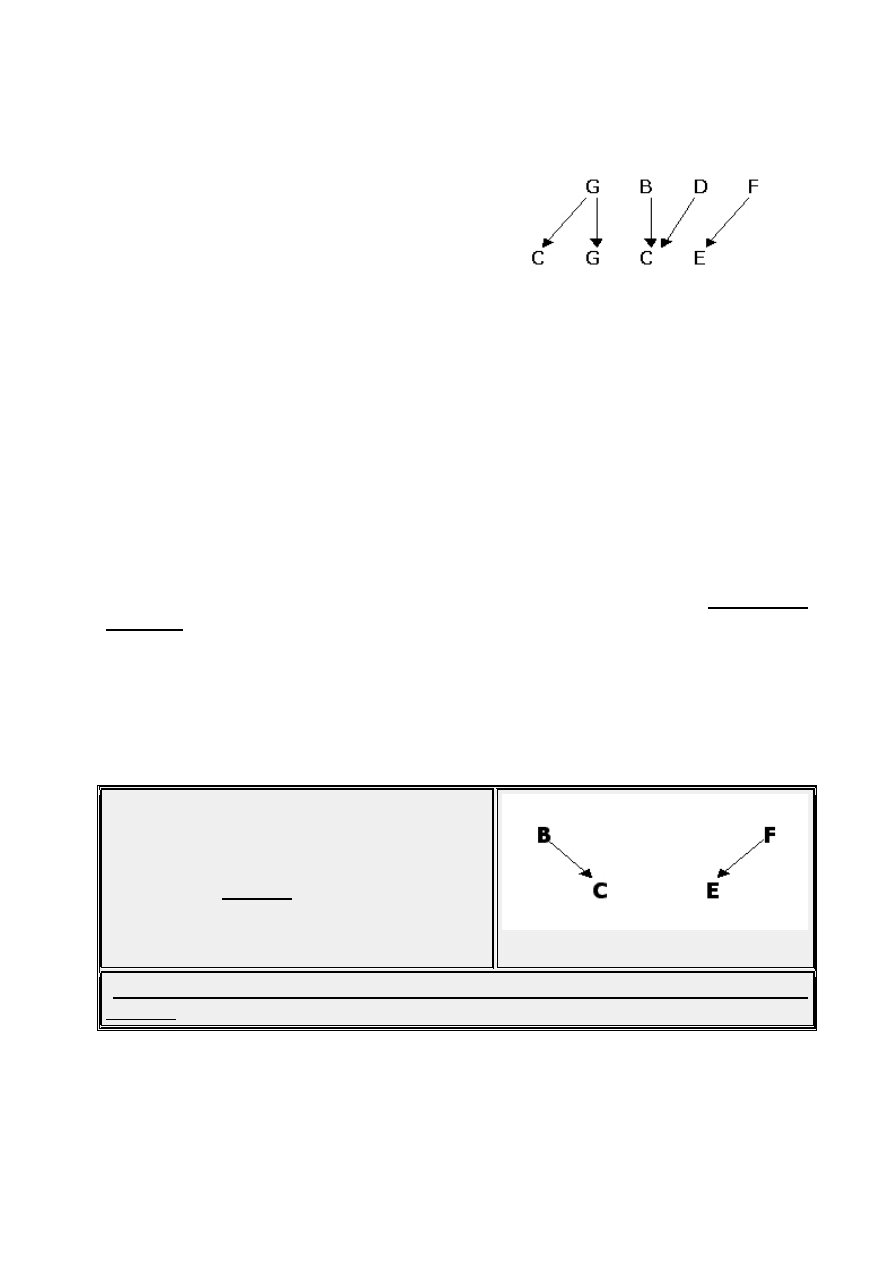
The table to the right shows an
idealized form of this resolution.
What, exactly, causes this resolution
to occur? Remember, we are dealing
with psycho-acoustic phenomena
which is highly subjective and the
topic of much debate down through
the ages continuing to the present
day. For now, let's put politics aside.

You are encouraged to do the following e
decide for yourself.

xperiment on a Piano or Guitar and

In the G

Chord, the root (G) and fifth (D) are quite consonant, as are the

root (G) and Major third (B). The Major third (B) and the fifth (D) form an
interval of a Minor third, also considered consonant, as do the fifth (D) and
the Dominant

(F). The interval between the root (G) and the

Dominant 7

(F) was considered dissonant in old classical theory. Most

modern theorists are not so strict and would consider the interval as colorful
if not downright consonant.

This leaves us with the interval B-F. This interval was actually outlawed by
the Medieval Christian Church and marked with the name Intervallo
Diabolo. This Interval spans 3 whole tones. There are many names for this
interval - diminished 5

, augmented 4

, #11

, and my favorite - TriTone. A

TriTone is naturally formed between the Major 3

and the Dominant 7

Because of the relative consonance of all the other intervals in the G

Chord,

most, if not all, of the tension in this Chord is caused by the presence of this
TriTone interval. Lydian-Dominant Theory is, literally, the study of
TriTones.

In Western Classical Music Theory, this
interval was always resolved inwardly.

We are now at the first really important place in Lydian-Dominant
Theory.

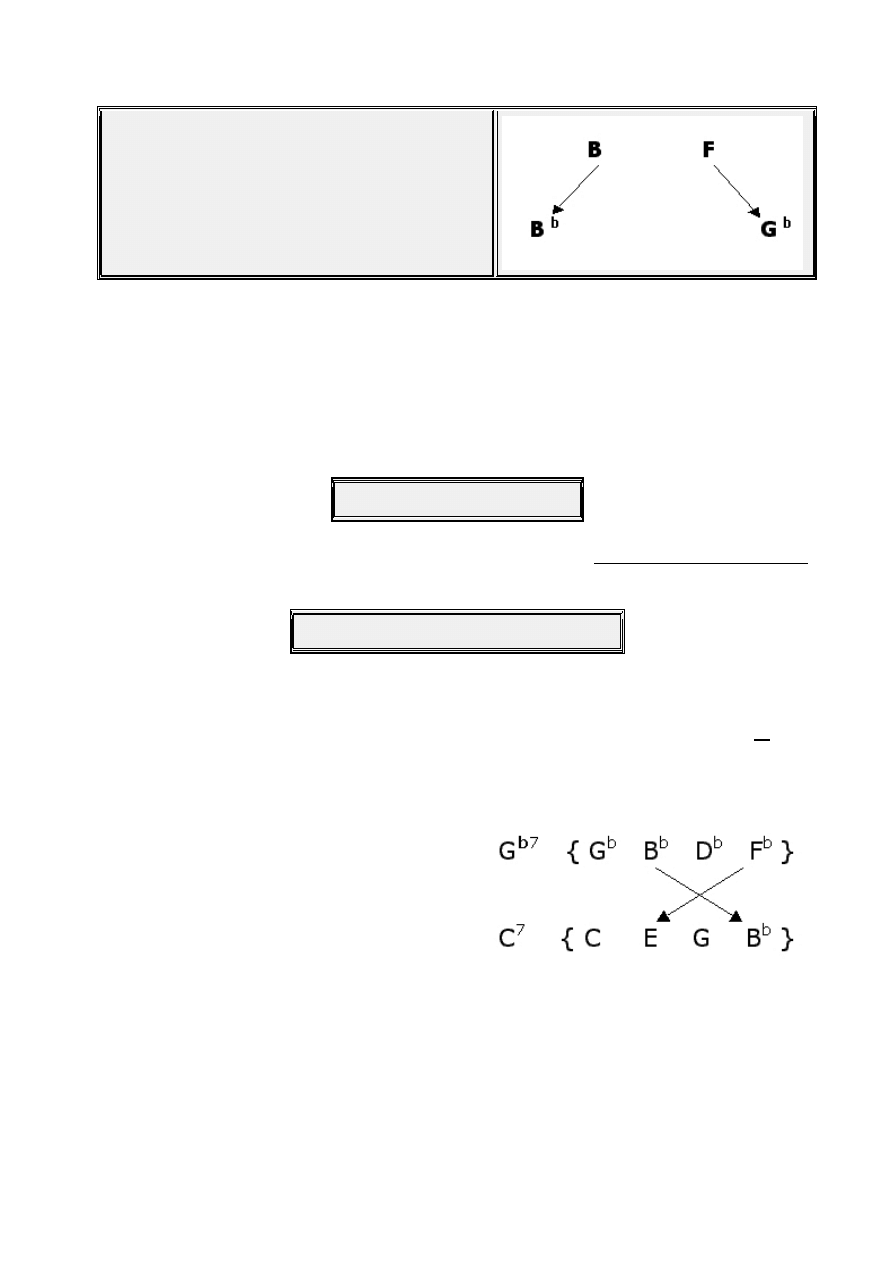
The TriTone interval also resolves
outwardly as easily and as naturally as
it resolves inwardly.

You should try this out repeatedly on a Piano and let your ear be your final
arbiter. These resolutions are symmetric and, I believe neither has any
precedence over the other. I agree with most modern theorists, that they
are equivalent and neither should be preferred for any subjective reasons.
So what does this mean???

All students of Jazz soon discover the ubiquitous Chord progression:

II m

» I Maj

Consider the Chord progression of the verse part of The Girl From Ipanema
by Antonio Carlos Jobim. It goes like this:

Maj

What in the world is that G

doing all over the place??? By classical rules,

this should be a C

as it is the Dominant 7

Chord in the Key of F. How

does the G

cause the desired resolution to the I Maj

Chord? This is the

heart of Lydian-Dominant Theory. In the table that follows I will spell out the
requisite chords, identify the relevant
TriTone - the rest is magic.

The operational TriTone is {E - B

}

(remember F

=E). Each of these

Dominant 7

chords has the same

TriTone !!! As stated earlier in the
analysis of the generalized
Dominant 7

, it is the TriTone that

causes the tension that gets resolved.

Notice also that C and G

are

themselves TriTones. Consider this. It would seem that the root (I) of the
Chord and it's closely allied 5

are quite exchangeable. It is the TriTone

Core of the Chord that is Invariant. We will see later just how ambiguous
TriTones can be. One can actually "get lost" aurally in an improvisation with

many sequential Lydian-Dominant changes in the Chord progression. Thus
the first Postulate of the Lydian-Dominant Music Theory.

Postulate 1

Any Dominant 7

Chord can be replaced by its TriTone equivalent

with no loss of resolving power.

This postulate is the Fundamental Assertion of Lydian-Dominant
Theory. Once we recognize the power of Lydian-Dominant structures and
introduce them into our music, we find that the word modulation takes on
an entirely new and exciting meaning. I would also add, that along with this
newfound modulating flexibility, a wealth of harmonic richness is also
realized. Classical music theory shortchanged itself terribly by banning
and/or ignoring this fundamental theoretical fact implied by the OverTone
Series and realized by the 12-Tone Tempered Scale.

Understanding and appreciating the fundamental assertion of the first
Postulate - TriTone Dominant Substitution - is but the beginning of our
journey. Next we will study and develop the essential core elements that are
the "building blocks" of Lydian-Dominant Theory - the TriTones.

Postulate 2

There are 6 TriTone pairs

= { c - f

} TT

= { a - d

}

= { g - c

} TT

= { e - a

}

= { d - g

} TT

= { f/e

- b/c

}

Each pair is associated with two interchangeable Dominant 7

Chords. That

is, they may be substituted for each other to provide harmonic richness
and/or chromatic movement as can readily be seen in the Chord progression
snippet from The Girl From Ipanema used above.

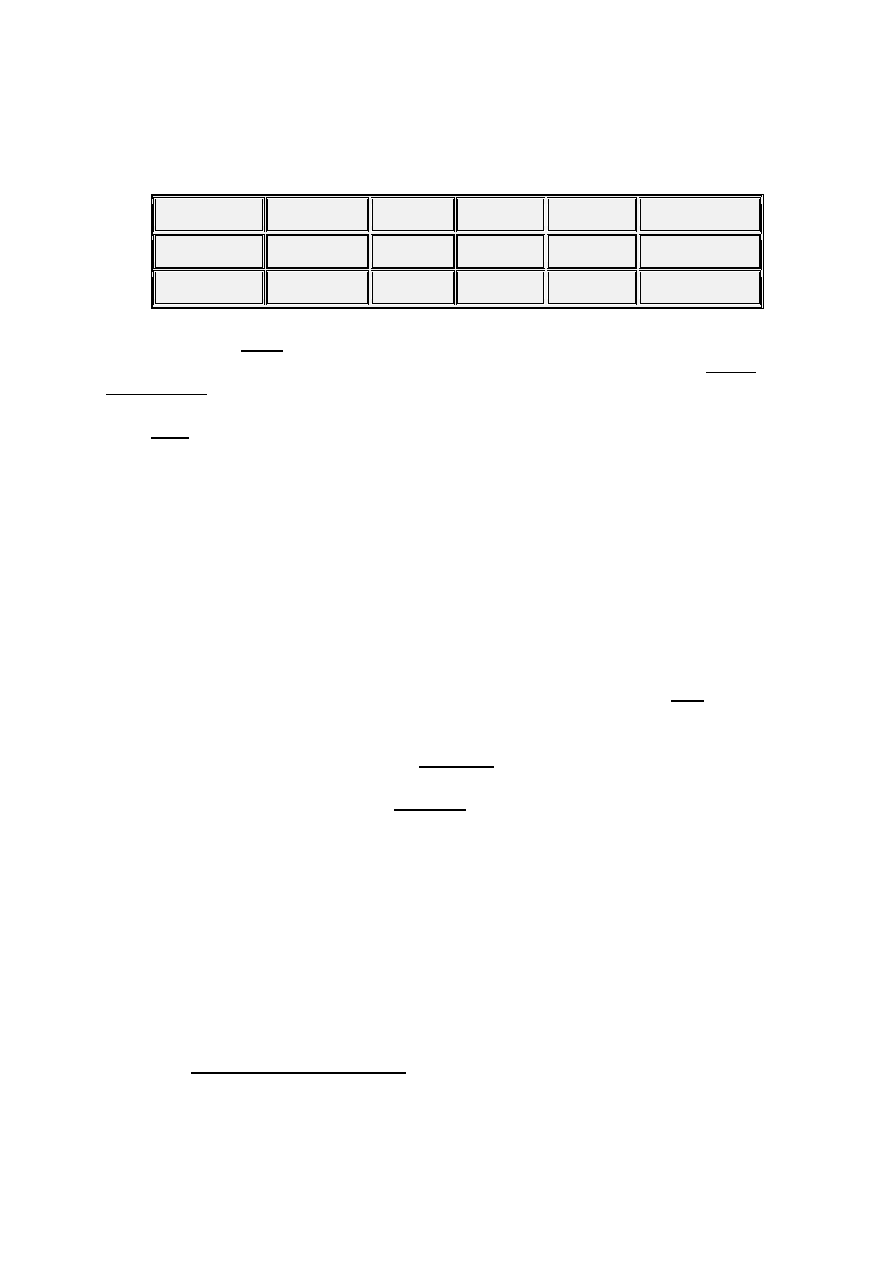
The following table enumerates the 6 Dominant

pairs and their associated

TriTones. Read this table up and down the columns - the involved TriTone is
in between.

- e/f

f/e

- b/c

c - f

g - c

d - g

a/b

- d

Now we know why that G

is there in Jobim's Song. In fact, all of his work

is heavily Lydian-Dominant. Check out his compositions Wave and
Desafinado to see what I mean.

The BIG Fact is, that Jazz is heavily permeated with Lydian-Dominant
Chord Progressions and Melodic development. Swing, Blues and their
derivatives in the Pop/Rock styles less so, but still Lydian-Dominant. South
American forms like Samba and Bossa Nova and Tango are, again, heavily
permeated with Lydian-Dominant Chord Progressions and Melodic
development. Likewise, the Afro-Cuban inspired Salsa forms. Certain 20

Century Classical Composers have also ventured into Lydian-Dominant,
Debussy, Ravel, Stravinsky to name just a few.

You should become aware of an odd thing with these pairs. Are they
augmented 4

ths

(

11) or are they diminished 5

ths

(

5)? In Natural Music

Theory (pure Harmonic Series intervallic evolutions), there is a definite
difference. In the 12-Tone Tempered System there is not. The very
process of Tempering obliterates any difference.

Indeed, the TriTone interval is an Artifact of the 12-Tone Tempered System
- it doesn't even exist in non-tempered systems. Approximations of it do
exist in pure Scale, in fact, an infinite number of them. But as the TriTone
has a value of p·2

(1/2)

, ( any starting pitch p times the square root of 2 ),

all the Harmonic Series (which is based exclusively on rational numbers)
can do is spit out closer and closer approximations to the TriTone. This is not
at all as weird as it seems at first glance. A famous Mathematical Proof,
attributed to Euclid, may be found in any high school Geometry textbook
showing that:

No rational number, that is, an number of the form a/b , where a, b are

natural numbers, can equal √2. TriTones are intimately related to this
number that caused the Pythagoreans so much trouble with ir-rational
numbers. This topic and other related items are explored in greater depth in
my book Natural Music Theory.

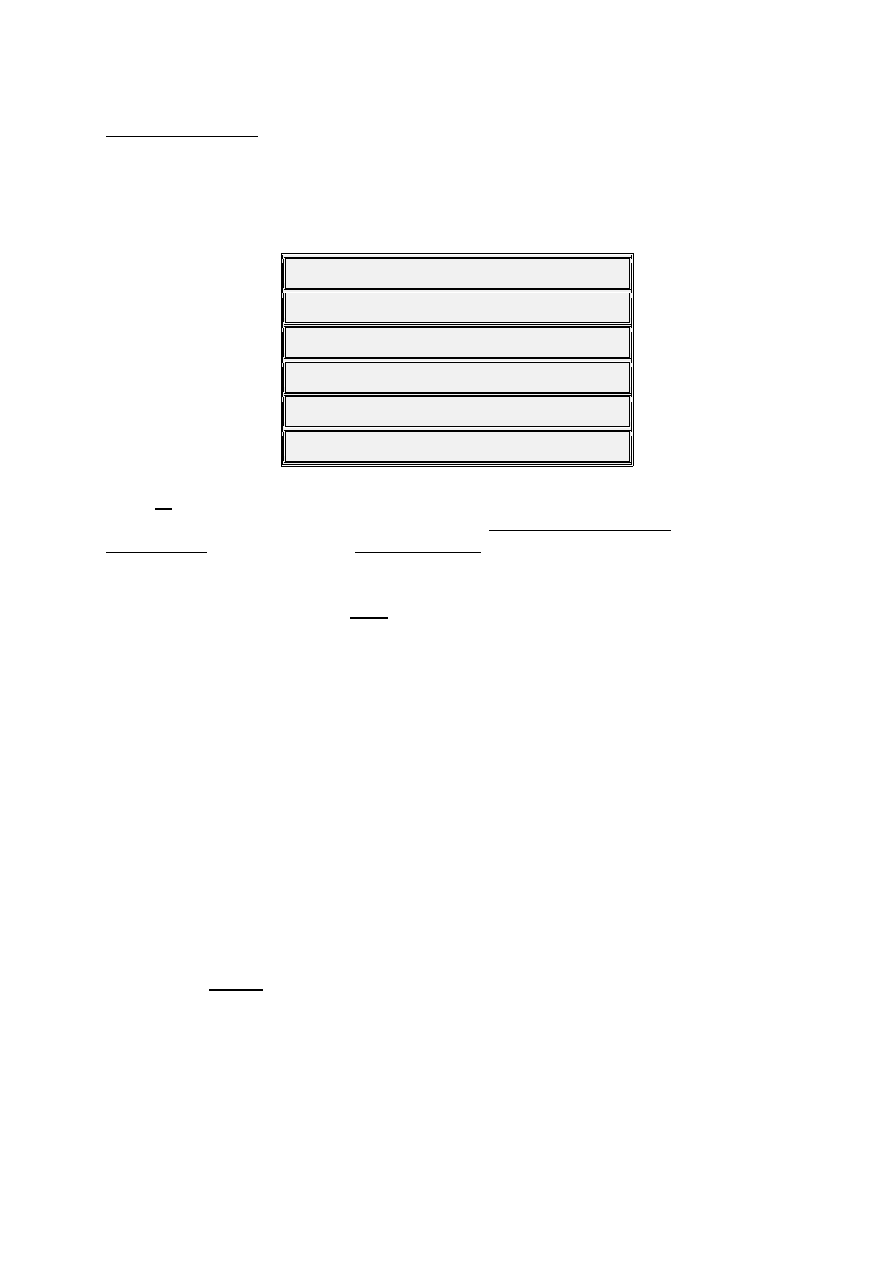
Postulate 3

There are 6 Dominant

7 b5

Chords.

7 b5

= F

#7 b5

= { C E G

}

7 b5

= D

b7 b5

= { G/A

B/C

F }

7 b5

= A

b7 b5

= { D/E

C }

7 b5

= E

b7 b5

= { A/B

G }

7 b5

= B

b7 b5

= { E/F

D }

7 b5

= F

7 b5

= { F A C

/B E

}

This is the quintessential Lydian-Dominant Chord. It is both Lydian and
Dominant. This Chord puts the 'A' in Take The 'A' Train, the 'Des' in
Desafinado, the 'Tune' in Bernie's Tune, and that special sonic twist in so
many Lydian-Dominant compositions.

The Chord is comprised of two TriTone pairs a Major 3

apart. In the case of

the C

7 b5

- F#

7 b5

pair, they are {c - f

} and { e - a

}. Play this

Chord - listen to it. Grab the 4 notes in the C-F

pair - { f

c e }. Now

play a C bass note - listen. Now play an F

bass note - listen. What do you

hear? I hear the same tonality in each case. Nothing really changes except
the voicing, i.e. a particular rearrangement of notes.

For the Improviser, this is really important. The first problem encountered
when analyzing a particular Chord progression is figuring out what Scale(s)
are implied by which Chord(s). It doesn't matter how fast your fingers are
or how good your tone is if you're playing the wrong notes - it'll still sound
bad. This is the major problem I have with some Improvisational Methods of
listing a seemingly different Scale to each and every Chord in a
progression. I find it more confusing than helpful, especially to the novice.

The fact is, that the underlying scalar note group frequently does not
change at all ! More often than not, whole sequences of Chord changes
define the same note group. It doesn't matter which notes in a particular
Scale you choose to include in a motif, its still the same underlying
tonality. This is why Handel sounds as homogeneously boring as a lot of
more modern music of all kinds - the whole song is defined by one
scalar group! You might see a lot of Chord changes, but all that is really
changing is which note(s) the bass player is currently emphasizing. For the
Improviser, nothing changes at all - its same Scale throughout.

Once the student progresses up to Lydian-Dominant, they find that what
looks like wicked hard Chord changes are really not so bad at all. There are
only 6 Dominant

7 b5

Chords, not 12 as with most other chords. This makes

learning them take half the time. All that remains is to fit them in properly.
Lydian-Dominant is actually easier than it looks. Things get even simpler in
the next postulate.

Postulate 4

There are 3 TriTone Quad Diminished Sub-Systems

= Cdim = E

dim = F

dim = Adim = { C E

A/B

}

= C

dim = Edim = Gdim = B

dim = { C

E/F

G B

}

= Ddim = Fdim = A

dim = Bdim = { D/E

F A

B/C

}

This is the infamous Diminished

Chord. As we can easily see, the quads

form 3 mutually exclusive sets of 4 notes. Each group is comprised of 2
interlaced TriTones a minor 3

apart. Notice that 4 super-imposed minor

rds

equals an octave in the 12-Tone Tempered System. This note group is

totally symmetric any way you look at it.

= TT

+ TT

= { c - f

} + { a - d

}

= TT

+ TT

= { g - c

} + { e - a

}

= TT

+ TT

= { d - g

} + { f - b/c

}

No group of notes has caused more problems for Music Theorists than this
one. Just naming the intervals is problematic within the old system. Below is
a technically correct naming of a C dim

Chord.

C - The Root - we'll see ...

- A Minor 3

above the root C - O.K.

- A Diminished 5

above C - A Minor 3

above E

- O.K.

- What shall we call this interval???

is a Minor 3

above G

and it is a diminished 5

above E

. But what

interval is it above C??? I have heard it called a diminished 7

. In

Standard Musical Nomenclature, 7

ths

are designated as major and minor

along with 2

nds

, 3

rds

, and 6

ths

- 4

ths

and 5

ths

are called perfect, and along

with roots, can be diminished, and, augmented. So what is a
diminished 7

???

I claim there is no such thing as a diminished 7

. This Chord is a 100%

total Artifact of the 12-Tone Tempered System. It doesn't exist at all in
any OverTone Series derived Systems. It is an emergent property of the
12-Tone Tempered System and is central to Lydian-Dominant Theory.
Interestingly, other Tempered Systems have analogous structures and are
discussed in depth in my book on Natural Music Theory.

B

/A is clearly a Major 6

(in disguise) above the root C. It acts like a 6

it sounds like a 6

, so why not call it a 6

!!! I seriously suggest that we

rename this wonderfully ambiguous Lydian-Dominant note set the
diminished 6

Chord - C dim

. As justification in addition to the above

analysis, I would point out that this Chord is remarkably close in sound and
function to the minor 6

Chord, a Chord more commonly used in older

American music, and still important in some indigenous styles like Tango.
This Chord has an ambivalent tonality and differs from the dim

in that the

is perfect rather than diminished.

= { C E

G A }

dim

= { C E

A }

Furthermore, if we invert the 6

in the C m

thereby changing the root note

to A instead of C, we derive the modern Jazz Chord, the A m

7 b5

- the so-

called half-diminished Chord. This Chord will be discussed in depth later on
in this treatise.

The dim

sub-systems also define 3 Lydian-Dominant Scalar entities called

diminished scales. They will be discussed later on in this treatise. The
diminished quads are integrally involved in several other important Lydian-
Dominant Chords which leads us to the next postulate.

Postulate 5

There are 3 Sets of Dominant

7 b9

Chords, one for each Diminished

Quad Sub-System.

Technically speaking, there are 12 of these chords. In Lydian-Dominant
reality however, they each fall into one of the 3 Diminished Quad Sub-
Systems. I will show this using:

DQ

= {c e

a/b

}

Consider the Chord:

F

7 b9

= { F A C E

}

As discussed before, most of the "action" (tension-release) in a Chord is
created by the 3

and 7

. In this Chord the

9 also contributes significantly.

Play this Chord alternating the

9 (G

)with the octave (F'). What does your

ear think of this? We already know that in a Dominant Chord, the 3

and 7

are a TriTone. In this Chord, the 5

and

form another TriTone! Once

again, as in the Dominant

7 b5

, there are two TriTone pairs in the same

Chord.

But this is a property of diminished quad sub-systems - is there one lurking
within this Chord. Sure is. The 3

, 5

, and

form a dim

Chord!

This is the substance of this postulate. The "action" in this Chord is caused
by every note but the root. This is one of the most striking aspects of the
Lydian-Dominant System - that roots are frequently extraneous to the
function of a Chord. They can be exchanged in certain proscribed ways.
In this case, DQ1 contains the "action" notes for:

7 b9

= { F + DQ

= ( A C E

) }

b7 b9

= { A

+ DQ

= ( C E

) }

7 b9

= { B + DQ

= ( D

A C ) }

7 b9

= { D + DQ

= ( F

A C E

) }

Notice also, that the exchangeable roots themselves form a dim

quad !!!

Grab the diminished quad on a Piano with the right hand. Now play each
root in turn and listen. Do you hear what I hear? The "action" notes are the
same no matter how you choose to voice them. Changing the root notes
alters the note set (thus the sonority changes), but the tension/resolution
mechanism is invariant. Lydian-Dominant is very cool. The same thing
goes for the other two quads and figuring them out I leave to you as an
exercise.

Don't forget - this note-group is in the Dominant

Chord-Space and, as

such, can be substituted for its TriTone equivalent! Lydian-Dominant is
wicked cool. A frequent companion of the X

7 b9

is the subject of the next

postulate.

Postulate 6

The minor

7 b5

/ minor

Chord.

As mentioned briefly above, this note group has a dual nature. It also called
the "half-diminished" Chord. This makes some sense in that it is formed
by adding a

7 to a diminished triad. However, this pseudonym hides the

fact of the dual nature of this Chord - it can be looked at as a 6

Chord or a

Chord, dependent on other factors such as melodic leading, resolution,

and rooted-ness.

7 b5

= { C E

}

= { E

C }

When used as a m

7 b5

, it is most commonly the first part of what I call a

minor

II-V-I:

Major

II-V-I

- G

- C M

minor

II-V-I

7 b5

- G

7 b9

- C m

Though this is the most common usage of this Chord, especially in Jazz
compositions, the subtle ambiguity of this note group lends itself to other
uses. It doesn't have to resolve to a

I m

Chord through the

7 b9

- it can

just as easily go other places though not anyplace. Check out Stella By
Starlight.

When this note group is used as a m

Chord, it is quite common to find it

used as a

Chord! There are innumerable songs that do this Remember, all

that has changed is the root note. It's the same basic tonality, but
emphasizing a different bass note gives this note group a different quality.
This note group is truly ambivalent in character and has power in many
different directions.

Actually, the m

7 b5

is the OverTone Series Inverse of the Dominant

Chord

making it an important fundamental theoretical construct - want to know

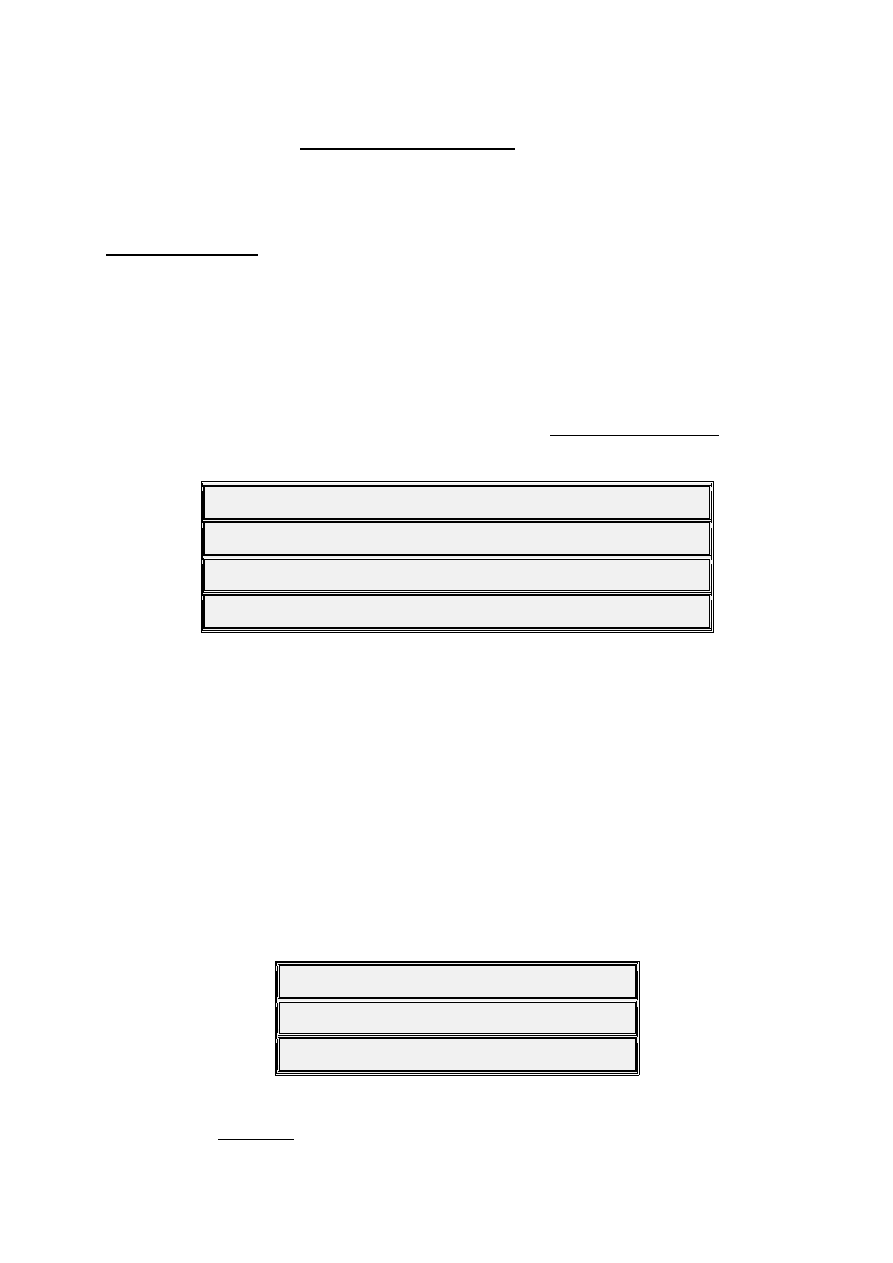
more? The derivation of this Chord and that of minor itself are presented in
depth in my book on Natural Music Theory.

Postulate 7

There are 4 Augmented Triad Sub-Systems.

Notice that 3 super-imposed Major 3

rds

exactly equals an octave in the 12-

Tone Tempered System. Like the dim

sub-systems, the 4 Augmented sub-

system triads are totally symmetric and form 4 mutually exclusive sets of 3
notes. They are:

= Caug = Eaug = A

aug = { C E G

}

= E

aug = Gaug = Baug = { E

G B }

= F

aug = B

aug = Daug = { F

D }

= Aaug = C

aug = Faug = { A C

F/E

}

Though not properly Lydian-Dominant, the 4 augmented triads are heavily
involved in Lydian-Dominant Theory in at least two important ways. First,
the scales that underlay this Chord are all Whole-Tone (altered) Scale
variants. These scales can also underlay other important Lydian-Dominant
Chords. I will have more to say on this later in this treatise. Second,
Augmented Triads are usually used as Dominant 7

or 9

Chords making

them Lydian-Dominant and subject to all the other Lydian-Dominant
Postulates.

Here's where the fun begins again. These 4 augmented sub-systems imply 4
corresponding Augmented

sub-systems as well. I'll show you the T

sub-

system and leave the other three for you to do as an exercise.

C aug

= { AT

= ( C E G

) + B

}

E aug

= { AT

= ( E G

C ) + D }

aug

= { AT

= ( A

C E ) + G

}

As with the diminished sub-systems, these augmented sub-systems are a
100% total Artifact of the 12-Tone Tempered System. As shown above in

Postulate 5, the X

7 b9

is essentially a diminished quad plus one of 4 related

roots, themselves forming another diminished quad. With these aug

note

groups, we have an augmented triad plus 3 related Dominant sevenths,
themselves forming another augmented triad!

The Aug

Chord is not as common used as many other Lydian-Dominant

Chords, but because it in the Dominant Group, it turns up in strategic
positions in many songs and must be handled properly. As mentioned briefly
above, the augmented sub-systems are intimately connected with Whole-
Tone Scales which brings us to our next postulates after a short digression.

Before we get to the next postulate I want to briefly discuss the Western
Classical bias (from the Greeks) toward the 7-note (so called) Dia-Tonic
Scale and an important bit of nomenclature

Despite the fact that we in the Western Cultures have come to enshrine
"Rational Thinking" as the epitome of human evolution, and view any
continued reliance on pre-rational systems as atavistic and downright
ignorant, we have nevertheless perpetrate on each unsuspecting generation
since the "Enlightenment" a plethora of number mystic systems which
are unquestionably accepted as "cosmic" Law.

Case in point - ask anyone why there are 7 days in a week and you will
usually get stunned silence and strange looks for a reply. Some will
desperately be mentally searching for a "logical" reason (there must be one)
for these commonly encountered systems. You may get a straightforward
"... and God rested on the 7

day." from a Religionist, and though I

respect their right to their strongly held convictions, I don't feel that I am
bound by them in any way. The point is, that there is No cosmic reason at
all why the number 7, or any other number for that matter, should be
specially favored.

In Music Theory, we use the two terms Scale and Chord without much
discretion. In fact, there is no real difference between them. It only depends
on how far we space out the intervals and even this is poorly defined. If we
space out the intervals in whole and half steps the note-group is usually
called a Scale. If we super-impose Major and minor thirds, it is usually
called a Chord. Problem is, some scales have intervals of a min 3

, and

some chords have intervals of whole step. I and many modern music
theorists use the term ChordScale. I also use the term note-group. This
makes more sense to me than trying to define a difference that does not
exist.

Consider the following analysis:

•

C-Major Scale = { C D E F G A B }

•

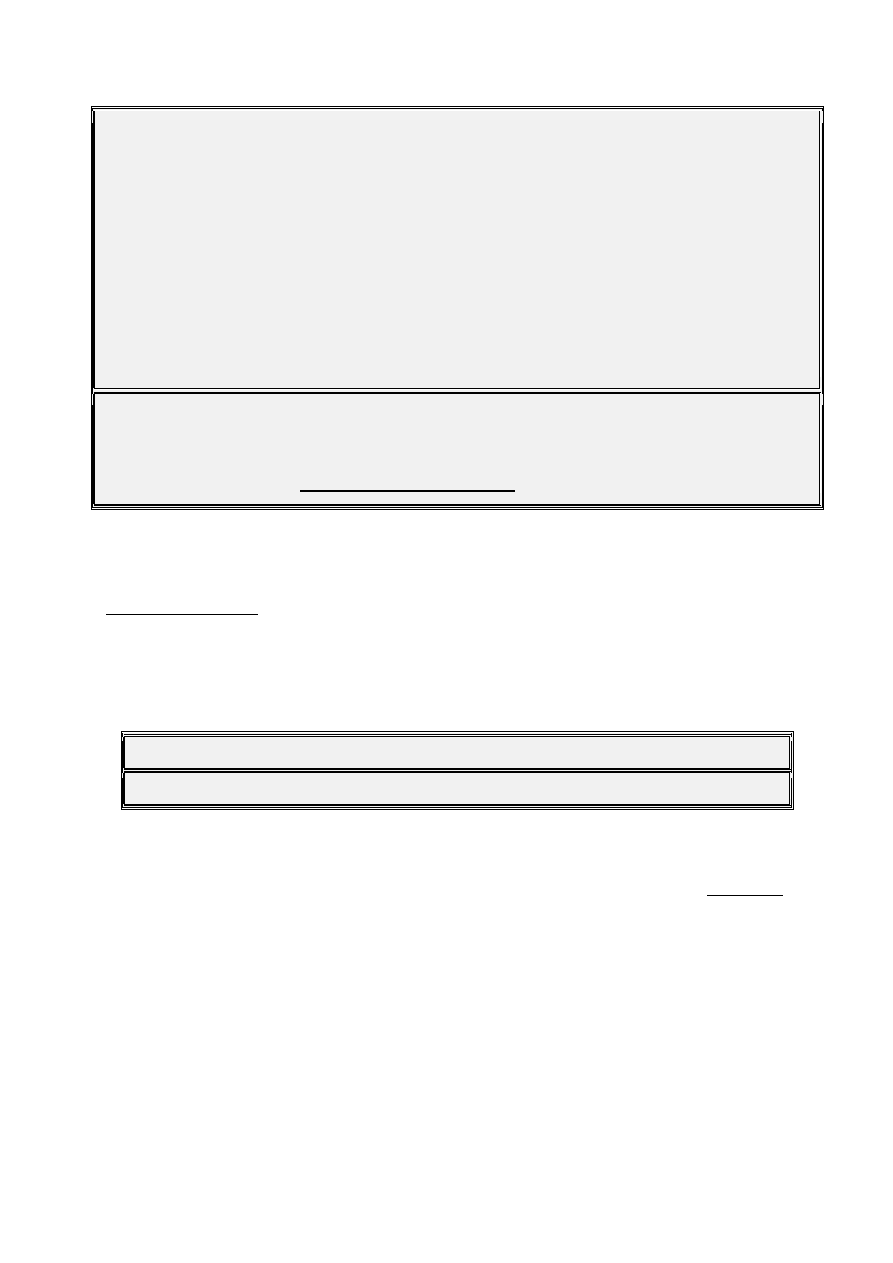
C Maj

Chord = { C E G B D F A }

A better way to show this is:

•

F-Major Scale = { F G A B

C D E }

•

Chord = { C E G B

D F A }

is in the Dominant

Group in the Key of F. In both cases, the note-

group is identical and the same ChordScale is defined. There happens to
be 7 notes in it and, indeed, there are a lot of 7-note scales. But, there are
many other ChordScales with a different number of elements that are just as
useful and legitimate as the dia-tonic.

The number 12 (as in 12-Tone Tempered System, inches in a foot, months
in a year, hours of day/night, and various groups of Apostles ) is also totally
bunged up with number mysticism. As usual, I discuss this issue in great
depth in my book on Natural Music Theory.

Postulate 8

There are 2 Whole Tone Scalar Sub-Systems.

= AT

+ AT

= TT

+ TT

= { C D E F

}

= AT

+ AT

= TT

+ TT

= { F G A B/C

}

This is a totally symmetrical Scale of 6 notes! It is constructed of nothing but
Whole steps. Play them on your instrument - was your ear fooled? They are
even more fun to sing - try it. This Scale is a Lydian-Dominant Artifact of
the 12-Tone Tempered System. It is not found in natural OverTone Series
harmonic derivations. Once again, tempering allows the "snake to eat its
tail".

The Whole-Tone Scale and its altered variants underlay many Lydian-
Dominant Chords. Basically, they fit any Chord with a diminished 5

or an

augmented 5

or both They can also be used when a

11 or a

13 is

present. I will show how they can be used to fit the common Lydian-
Dominant Chord - the Dominant

7 b5

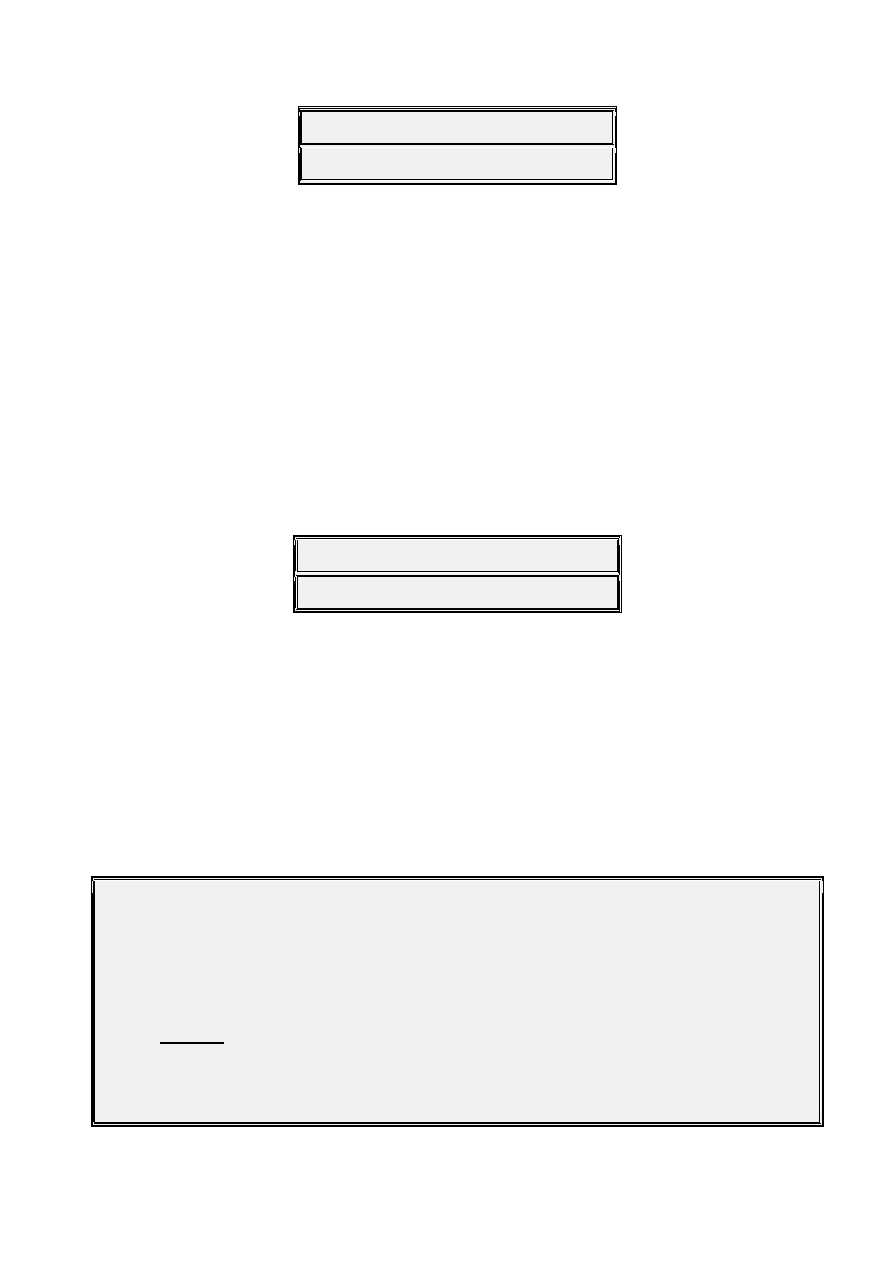
= { C E G

}

= WT

= { C D E G

}

Notice that we have 4 notes of WT

already in the Chord itself! The two

notes that are missing are D and A

. The D is easily justified as a 9

. As 9

ths

are, in reality, only the 2

note of a Major Scale, and this is a Major Chord,

it can always be used in a situation like this. The A

is more of a problem to

justify. Technically, C

is a Major Mode Chord and as such, a Major 6

should

be played giving us an A rather than an A

. Indeed an A can be played

turning our Scale into one of the many Whole-Tone variants. However, using
the A

gives us a slightly "outside" sound. In particular, it provides sonic

variance using a non-critical note - the 6

. This is very important to the

Improviser.

Next, I'll show how the Whole-Tone Scale can be used to fit an
augmented 7

Chord.

C aug

= { C E G

}

= WT

= { C D E F

}

Notice that we have 4 notes of WT

already in the Chord itself! The two

notes that are missing are D and F

. As above the D is easily justified as a

. This time, the F

is the problem to justify. Strictly speaking, as this is a

Major Chord, we should have an F rather than a F

. Indeed an F can be

played turning our Scale into a Whole-Tone variant. However, using the F

gives us a slightly "outside" sound. In particular, it provides sonic variance
using a non-critical scalar note - the 11

. This is very important to the

Improviser.

A comment on "playing outside"

Jazz players are famous for "playing outside" (i.e. playing non-chordscale
implied notes) in the course of their improvisations. Indeed, it is an
important part of the Jazz Style. I believe, however, that not all "outside"
notes are justified at the theoretical level. Some "outside" notes are just
plain wrong - i.e. not at all justifiable within the structure of the Chord
progression. Too often, "playing outside" is used as an excuse for playing
wrong notes due to an inadequate analysis of the Chord Progression implied
Harmonic Structure of a piece.

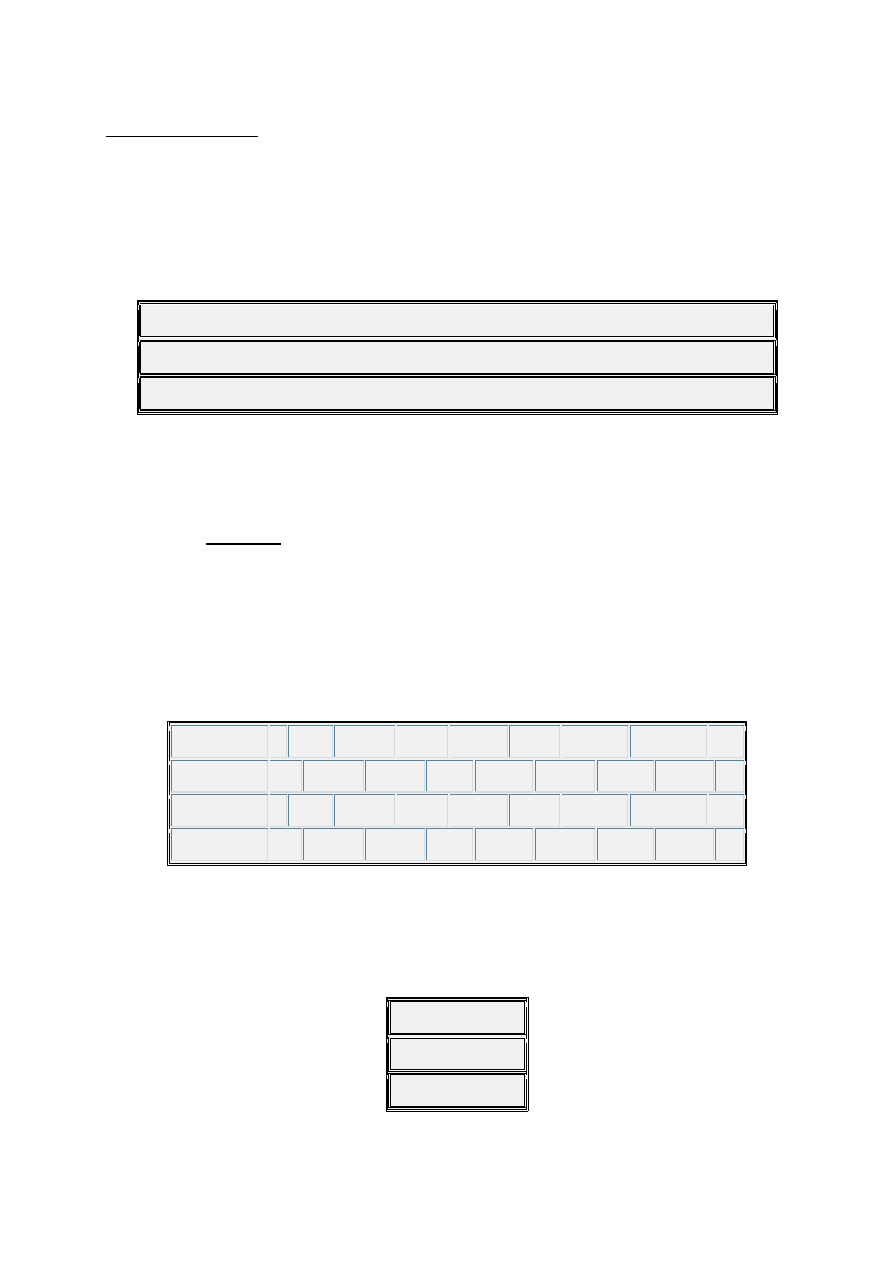
Postulate 9

There are 3 Diminished Scalar Sub-Systems.

= ( DQ

+ DQ

) = { C D E

F F

A/B

B/C

}

= ( DQ

+ DQ

) = { G A B

C C

E/F

}

= ( DQ

+ DQ

) = { F G A

B C

D/E

E/F

}

This is a totally symmetrical Scale of 8 notes! It is constructed of alternate
Whole and Half-steps. Play them on your instrument - was your ear
fooled? They are even more fun to sing - try it. This Scale is a Lydian-
Dominant Artifact of the 12-Tone Tempered System. It is not found in
natural OverTone Series harmonic derivations. Once again, Tempering
allows the "snake to eat its tail".

The diminished Scale comes in two flavors DS

and DS

depending on how

the diminished Scale is constructed - whole step first or half-step first. The
following table shows the difference.

DIM(wh)

= C D

A/B

B/C

DIM(hw)

= C C

E/F

Notice that C

DIM(hw)

= C

DIM(wh)

!!! All we do is start on a different note in

scalar sub-system. This is generally true of every one of these scales leading
to the following relations.

wh1

= DS

hw2

wh2

= DS

hw3

wH4

= DS

hw1

There are many ways to use these scales. In either flavor, they remain
wonderfully ambiguous and their use now and again over the proper Chord
changes, though tricky, creates much sonic richness. I will show some ways
to use these scales and leave others for you to investigate as an exercise.

I will use the classic Lydian-Dominant Chord progression elaborated on
extensively above:

The Lydian-Dominant

II - V - I »»» IIm

- I Maj

Let's work in the Key of C. The Chord progression we need to fit is: Dm

- CMaj

- the x signifying some form of Major Chord like a C

, a CMaj

or a CMaj

LD II-V-I Dm

CMaj

DIM(wh-up)

(D E F G) (A

) D'

Set

DIM(wh-down)

(D' C B A) (A

F E

) D

Notice that there is an Up and a Down version of the Scale, both being
constructed of alternating whole & half-steps. The Scale D

DIM(wh)

composed of 2 sets (called tetrads from Greek Music Theory) of 4 notes. In
the Up version, Set

is the first 4 notes of a Dm Scale and Set

is the first

4 notes of a A

m Scale. In the Down version, Set

is the last 4 notes of a

Dm (Dorian as implied by the Key of C) Scale and Set

is the last 4 notes of

the corresponding A

m Scale.

I hope by now that you have noticed that D & A

are TriTones !!! This

shouldn't be a surprise to you anymore. Play the chords and the
accompanying scales on the Piano - listen. They are super-diminished every
way you look at them. Try playing them in "thirds" - in "fourths". See if you
can find other ways to use these wonderfully ambiguous Scale patterns.

For now, I will conclude this treatise with an excerpt from my book on
Natural Music Theory. It deals with the actual OverTone Series implied
note-groups that underlie Lydian-Dominant Theory. To appreciate its
simplicity one only has to look carefully at the OverTone Series and list the
note-groups by Doublings.

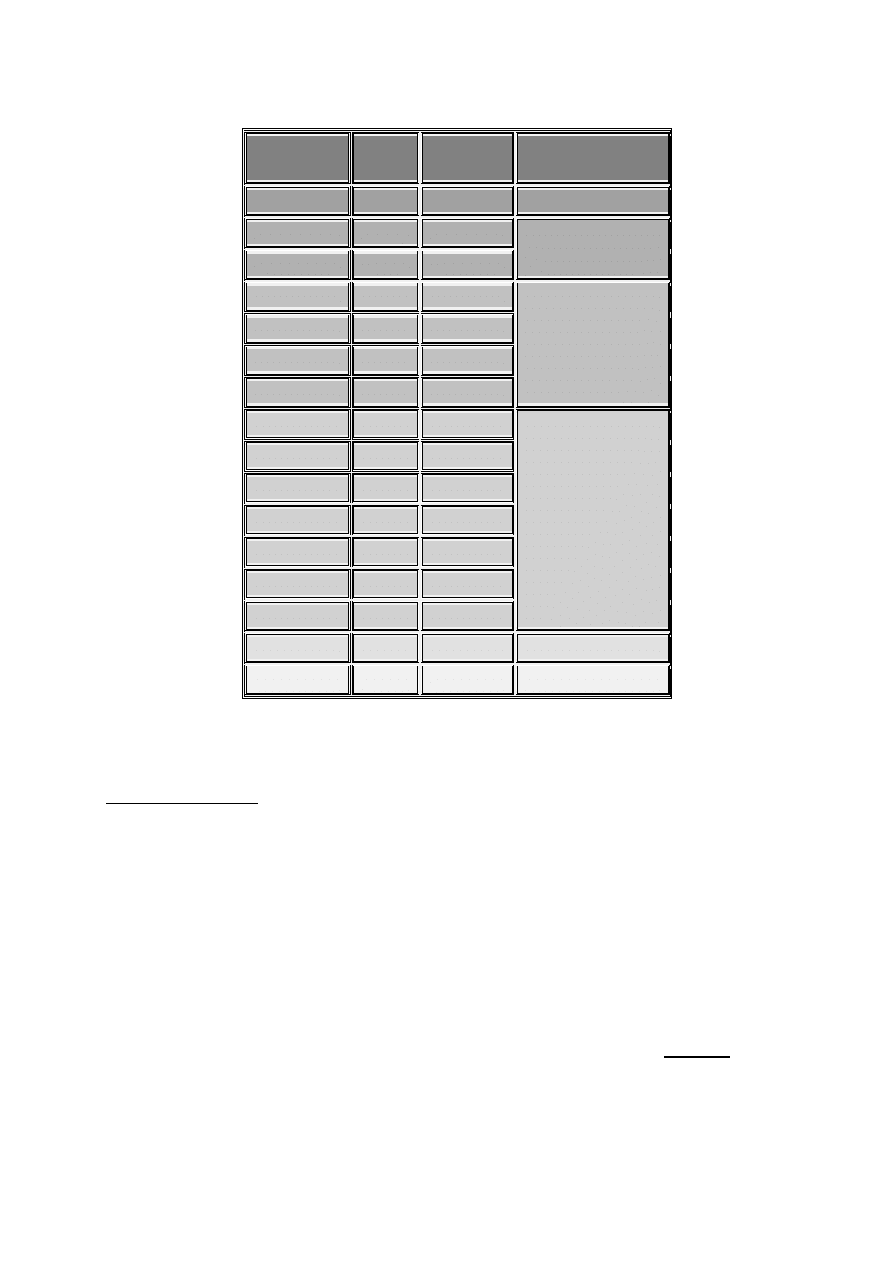
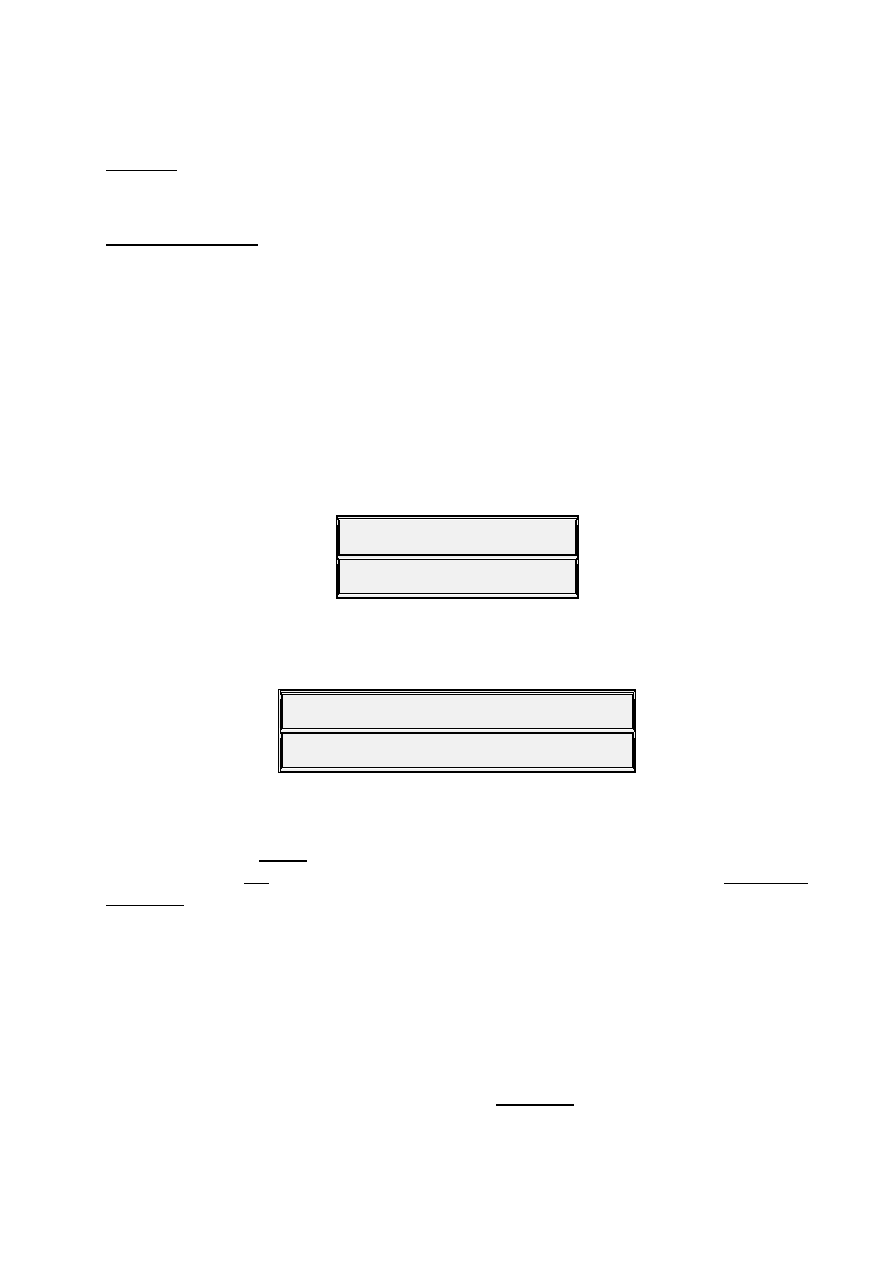
OverTone Note

Note
Name

Analysis

Fundamental

Fifth

Dominant

Lydian-Dominant

Scale

Leading Tone

Doubling

Postulate 0

The Primal Lydian-Dominant ChordScale

» { C D E F

G A B

}

This ChordScale is Legendary. It is found the world over and is usually
associated with the local culture's Goddess. Notable among these are the
Greek Sappho of Lesbos and the Hindu Saraswati - Goddess of Music,
Mathematics & the Sciences. It is a wonderful Scale and wholly derived
from the OverTone Series generated Harmonic Series. This knowlege is
Ancient! Most people today don't know that Plato, Aristotle, Euclid, Ptolemy,
and who-knows-how-many others wrote extensively about Music Theory. It
is written about in the Vedas, the World's oldest books. It is amazing to me

to be constantly re-discovering facts known to humans so long ago and then
forgotten in the headlong rush of Civilization's March.

Discussion based on the previous OverTone Series Table:

Note the 'natural' note-group progression:

•

First, you produce a Pitch, any Frequency

•

Next, you get a Doubling (see below)

•

Then, a 5

- the first interval created that is not a Doubling. This interval

(3/2)

generates the 12-Tone Tempered (Pythagorean) Scale

•

Then, you get a Chord - C

- The Dominant

Chord. It is 100% naturally

derived from the OverTone Series.

•

Lo and Behold, this Chord implies the Lydian-Dominant Scale - C

, not

the Pure Major, nor the Myxo-Lydian as older Music Theories claim.

•

A Leading-Tone into the next Doubling. I will have more to say about this
concept in the book.

•

The process continues to Infinity with new chordscales emerging that
transcend and include those already manifest. As usual, I discuss this issue
in great depth in my book on Natural Music Theory.

Notice my use of the word "Doubling" instead of "Octave". The word
octave contains a built-in and totally unwarranted bias toward 7-note scales
- it literally means the "eighth" note. It is true that there are many
wonderful and important 7-note Scales, but this fact hardly justifies priority
status. Doubling is a Psycho/Physio-Acoustical phenomenon - it has nothing
at all to do with scales.

Concluding Remarks:

As we continue our studies, I will point out Lydian-Dominant elements
where ever they occur in the Songs we learn and the Improvisations we
create for them. Regularly and methodically practice the preparatory
exercises that I have created for you to learn the Lydian-Dominant System.
Your hard work and diligence will reap great rewards as your Improvisations
develop the tremendous sonic richness implicit in the Brave New World of
Lydian-Dominant Music Theory.

Norm Vincent

NorthStar Studios - April 2000
Norm@LydianDominant.Com

Wyszukiwarka

Podobne podstrony:
(Sheet Music) Theory Bob Taylor Jazz Improvisation Book 200 Standards Bb
Music theory and improvising outline
Music Theory Finishing the Blues (For Now) John Duarte
Music Theory Quick Facts Sheet
Dans Music Theory
Music Theory John Dowlands Chromatic Harmony (John Duarte)
Music Theory Basic Level
Music Theory Is Not Nuclear Physics
Music Theory Shades of Blue (John Duarte)
Analysing Popular Music Theory, Method And Practice By Phi
The Beatles Hey Jude song chords and lyrics for guitar music downloads pdf
Boceto Andaluz uit The Guitar Music of Spain Volume One Bartolome Calatayud
Foundations of diatonic theory a mathematically based approach to music fundamentals The Scarecrow
Juslin, Slobada Music and emotion theory and research str 71 134
(ebook PDF)Shannon A Mathematical Theory Of Communication RXK2WIS2ZEJTDZ75G7VI3OC6ZO2P57GO3E27QNQ
Goertzel Theory
Hawking Theory Of Everything
Maslow (1943) Theory of Human Motivation
Habermas, Jurgen The theory of communicative action Vol 1

więcej podobnych podstron