
Autor: Martin Slota
Zdroj: http://www.zones.sk
Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú
č
ely a akéko
ľ
vek verejné
publikovanie je bez predchádzajúceho súhlasu zakázané.
1/3
MATURITNÉ PRÍKLADY Z MATEMATIKY
M
ATURITNÝ OKRUH
7:
M
OCNINY
1. príklad (82/Pr. 4)
Zadanie: Ur
č
te, ktoré z
č
ísel
e
e
π
π
,
je vä
č
šie.
Riešenie:
Vyjdeme z hypotézy, že
e
e
π
π
>
, a tú dokážeme, alebo vyvrátime. Nerovnicu zlogaritmujeme pri
základe
e
:
π
π
π
π
ln
ln
ln
ln
>
⋅
>
⋅
e
e
e
e
Teraz vyšetríme priebeh funkcie
( )
x
x
x
f
ln
=
na
π
,
e
:
( )
2
ln
1
x
x
x
f
−
=
′
Ke
ď
že prvá derivácia funkcie
f
nadobúda pre
č
ísla vä
č
šie než
e
záporné hodnoty, je funkcia
f
klesajúca na intervale
)
∞
,
e
.
Ke
ď
že
π
<
e
, platí aj
( ) ( )
π
f
e
f
>
a naša hypotéza je dokázaná (
č
iže
e
e
π
π
>
).
2. príklad (83/7)
Zadanie: Ur
č
te hodnotu sú
č
inu, ktorý má nekone
č
ný po
č
et
č
inite
ľ
ov:
K
⋅
⋅
⋅
⋅
16
8
4
3
3
3
3
(Tento sú
č
in
chápeme ako limitu postupnosti
č
iasto
č
ných sú
č
inov podobne ako pri sú
č
te nekone
č
ného radu.)
Riešenie:
Najprv si výraz upravíme:
K
K
+
+
+
+
=
⋅
⋅
⋅
⋅
16
1
8
1
4
1
2
1
16
8
4
3
3
3
3
3
. Teraz nám už sta
č
í vypo
č
íta
ť
sú
č
et
nekone
č
ného radu
∑
∞
=
=
+
+
+
+
1
2
1
16
1
8
1
4
1
2
1
n
n
K
. Podaktorí asi už vedia, že to bude 1, ale to by na
mature asi neobstálo, takže sa to pokúsime vyjadri
ť
pod
ľ
a vzorca.
∑
∞
=
1
2
1
n
n
je teda nekone
č
ný
geometrický rad s kvocientom
2
1
=
q
a prvým
č
lenom
2
1
1
=
a
. Jeho sú
č
et je teda
1
2
1
1
2
1
1
2
1
1
1
=
−
=
−
=
∑
∞
=
q
a
n
n
.
Teraz už iba dosadíme:
3
3
3
3
3
3
3
3
1
2
1
16
1
8
1
4
1
2
1
16
8
4
1
=
=
=
=
⋅
⋅
⋅
⋅
∑
∞
=
+
+
+
+
n
n
K
K
3. príklad (83/11)
Zadanie: Ur
č
te všetky reálne
č
ísla
x
, pre ktoré platí
0
1
1
5
6
≤
−
+
−
x
x
x
.
Autor: Martin Slota
Zdroj: http://www.zones.sk
Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú
č
ely a akéko
ľ
vek verejné
publikovanie je bez predchádzajúceho súhlasu zakázané.
2/3
MATURITNÉ PRÍKLADY Z MATEMATIKY
M
ATURITNÝ OKRUH
7:
M
OCNINY
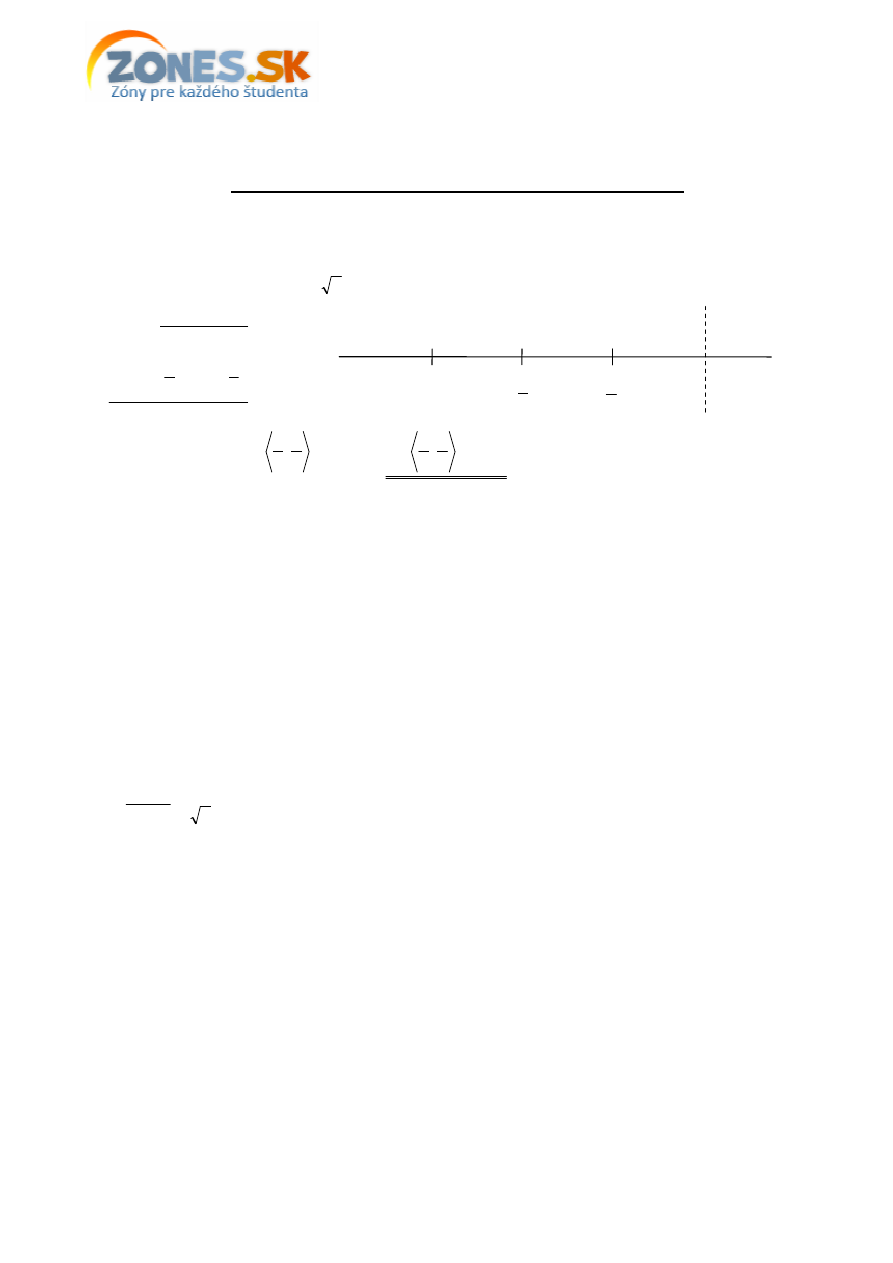
Riešenie:
Zavedieme si substitúciu
x
y
=
(takže
0
>
y
) a nerovnicu upravíme:
0
1
3
1
2
1
6
0
1
1
5
6
2
≤
−
−
⋅
−
⋅
≤
−
+
−
y
y
y
y
y
y
Výsledok teda je:
( )
( )
∞
∪
∈
⇒
∞
∪
∈
,
1
4
1
,
9
1
,
1
2
1
,
3
1
x
y
.
4. príklad (83/13)
Zadanie: Pre každé kladné celé
č
íslo
n
platí
(
)
1
5
8
40
|
28
+
−
−
n
n
n
. Dokážte.
Dôkaz (priamy):
Výraz
si
upravíme:
( ) ( ) ( ) ( )
1
5
1
8
1
5
1
5
8
1
5
8
40
−
⋅
−
=
−
−
−
⋅
=
+
−
−
n
n
n
n
n
n
n
n
.
Platí
vzorec
(
)
(
)
(
)
1
2
2
3
2
1
−
−
−
−
−
+
+
+
+
+
⋅
−
=
−
n
n
n
n
n
n
n
b
ab
b
a
b
a
a
b
a
b
a
K
, a preto:
( )
(
)
( )
( )
(
)
( )
( ) ( )
(
)
(
)
1
5
8
40
|
28
1
5
1
8
|
28
1
5
|
4
1
5
5
5
1
5
1
5
1
5
1
8
|
7
1
8
8
8
1
8
1
8
1
8
2
1
2
1
+
−
−
⇒
−
⋅
−
⇒
−
⇒
+
+
+
+
⋅
−
=
−
=
−
−
⇒
+
+
+
+
⋅
−
=
−
=
−
−
−
−
−
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
K
K
Č
BTD.
5. príklad (84/22)
Zadanie: Ur
č
te všetky reálne
č
ísla
x
, pre ktoré sa štvrtý
č
len binomického rozvoja výrazu
(
)
6
12
log
1
2
1
+
+
x
x
x
rovná 200.
Riešenie:
Všeobecný zápis binomického rozvoja je:
(
)
∑
=
−
−
−
⋅
=
+
+
⋅
+
+
⋅
+
⋅
=
+
n
i
i
i
n
n
k
k
n
n
n
n
b
a
i
n
b
n
n
b
a
k
n
b
a
n
a
n
b
a
0
1
1
0
K
K
Pre náš konkrétny prípad:
nedef.
+
+
–
–
2
1
3
1
0
1

Autor: Martin Slota
Zdroj: http://www.zones.sk
Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú
č
ely a akéko
ľ
vek verejné
publikovanie je bez predchádzajúceho súhlasu zakázané.
3/3
MATURITNÉ PRÍKLADY Z MATEMATIKY
M
ATURITNÝ OKRUH
7:
M
OCNINY
(
)
( )
(
)
(
)
(
)
(
) (
)
0
1
4
0
4
3
1
4
4
7
log
10
log
log
log
1
4
log
1
6
10
200
20
200
3
6
2
2
log
1
4
log
1
6
4
1
log
1
2
3
3
12
log
1
2
3
=
−
⋅
+
=
−
+
=
+
+
=
=
⋅
+
+
+
=
=
⋅
=
⋅
⋅
+
+
+
+
+
+
y
y
y
y
y
y
y
x
y
x
x
x
x
x
x
x
x
x
x
x
10
1
10
4
4
=
⇒
=
=
⇒
−
=
−
x
y
x
y
{
}
10
,
10
4
−
=
K
Wyszukiwarka
Podobne podstrony:
3 6 Mocninne funkce
Mocniny
więcej podobnych podstron