/
!"
/
# $%
&'( !"
/
)*+*
, -
./ 0 1 2/13 ( 4 % 0 5 6
(Melia azedarach)
16
(Morus alba)
!% 57 8 (
0 $ 9 '
)
*
! / :
;
0 6 $ :
*
5 5 < :
;
$= 9 $>
?
)
:
/
/
:
/
/
(
"
@
#
4
A B
C #
!% 57
' 8 ( 0 1D ( E 9 /C
% 0 5 F
G
G'
EG% 9 GH > G'
E #
( 57
8 E
.
#( ( G16
G ./ 0 1 1D (
J ( % E
0 5 F 4 K6
( G4
( G
L :M9 N L M % ED ( 2/13
M
> (
!
( # O ( P ( - >
( :2/13 F 6 ( 0 1D ( Q RS
6 N
0 57 %
% < '
.
MT1U V1 0 6 F 1U V1 0 6 ( 4 F 0
J 5<
9 ( 9 ( < L/13 '
( 4 % 0 5 F $3
6
J
S #( L1 (
0
>
J ( F # %
J #
.
5< W 1
F ( 9 ( ( 0
'
/$X 6" : RD Y
Z
0
J [ A F
:# % \
'
MG S 0 G6 G $1 GO Y G :E
$
7S
#
( 4 F $3
F
%
J
./ 0 1
J ( ( 0
> ( #
)
M9 N L
^_
/
`
=
R
2
6 N L :
b_
/
`
=
R
2
Q RS :
b_
/
`
=
R
2
(
16
)
M9 N L
b`
/
`
=
R
2
6 N L :
?`
/
`
=
R
2
Q RS :
bd
/
`
=
R
2
(
%
4
.
F 1G
G J ( ' ( F 6e$'
#
( 4 % E
F , 5 0 5$' # %
J
)d
% # ( 0 1D ( # UD % A % Q RS ( O
.
#f
'
/9
:
0
J :F :./ 0 1 : 16
: % ( 4
.
!"
#
$%&
' ( !"
)* +
$! ,- . / 01 '& 2 # 3 & 4 ')5 !" #
.
$! ,- . / 01 '& 2 6 !"
$%&
' ( !" #
)* +
& 4 ')5 !" #
$! ,- . / 01 '& 2 # 3
.
1" 3 '& 2 6 !"
$%&
' ( !" #
)* +
'& 2 # 3 & 4 ')5 !" #
1" 3
.
%"
$! ,- . / 01 '& 2
$%&
' ( !" #
)* +
! ,- . / 01 '& 2 # 3 & 4 ')5 !" #
$
*
:
7 , 8+ 9 :;+
#
86!& 8<" ;
$
:
zkarimianf@gmail.com
Downloaded from jcpp.iut.ac.ir at 13:57 IRDT on Wednesday May 3rd 2017
/
!"
/
# $%
&'( !"
/
)*+*
==
T
9 >"
1
?*+ 3" $8 $ @ 3 A B
C D;+ E
$DD+
*DDF G,DD% DDH $DDI" J
)DDF .
.
E DD! 3 DD% *F
K+ ! .
K.
*F G,% L H G
$MMN $ 6< O 7 >
$+ AP K. $*Q ? K ')+P
L DH $ " D RL D K. )!"
F
@+
*F S6T+ 6U6
" &
+
)
V
.(
H W,< -
B
S6T+ A
&
%" KQ" +
&)T+ .
*F L
X DU " Y! 3" Z 0[+ 6O\& K. A)6% " . ) . A B
KB F
;2 #] 0. / (@L
K KO% & K@ [^ # L
A&)D. DL
6< O 9_ B"
"
" " $! D+" 6 / D;Q" & $! D;!" L
)@F . $ F K0> & H
.
B S " F 2"
Y! E " 3" A
" DD. ')DDF DD " $DD P 7_8DD + )DDF . `DD% @+ )DDF " DD.
' 6
' Q # L&
A a B % # L
*DF DL 0. D # DL
)
WD> MB
$2)@!" & $ a@L" ? _1
(
& CDB" 7"G6* & C %& K60 &
$+ b I & K RL E6+3 3" A& 6.
c DL K. 3 6! & )! F
. )L" N! )O. CI" +
)
.(
K0D> D 1 /)1 $ J 3"
K %
" d J 3" A B E6. `% @+
D. . ^ & $L
AP )DF 9_ B"
" e1 . f0 N+ g. @+ %
DF $D+ DL
)
h
.(
DDY@+
DDaO+
#
DDY! KDD[i! 3" KDDj A DD B DD
A"GD6+
D+ $L 2P K. $ B @F , 3 K,@Q 3" Kj & $8 k < "
l [^ & X U "
%" K ;."& B
.
6O^ + & $. H
$. D
E DF" D.
*DF L B % . m , " ')F A B
$D+ &
%" ;6+ B )F 3" $ 7 1_J"
$DI" J )D!"
$DO^"& & DD *. DDY@+
DDaO+ DF
)DD@ ?L" DD
DD
)
.(
A DD B fDD0 N+ DDO." E6DD. SDD."& DD. DDQ + 7 DD1_J"
Wn DDaO+ G,DD% DDH
&
DD%"
DD 7")L DD + c DD%" DD.
R6D c D%" . W,< -
7 D> KD. A D B )DF 1 D% $D@6.
$U6
)
g D% $D06B & g D% #SD% + #K D;LP )F
(
A&)D. &
$D+ ' " o6D\ $D\ & $Da
i+ 3" ' U %"
DF
)
&
=
.(
9)+
DB O." . $@ ,+
)O + )F $\ S."& & L
KD! 2 3"
6;.
DL
$D B $D0(@Q
)
#
V
&
(
GD6! &
K! 2 3" $B .
D%" ')DF *@ 6 G,% H $ B L
)
#
&
(
&
&)DT+ 7 Di6iT & 7 DO< [+ A D@ D +"
9)+ E66O
AP ED% &
DB DO." E6D. $\ S."& & L
DL
K. G6! p)!" " + E6aL K
" Q&
7& U C6<
E6D. L
K! 2
& "
9)+ $a60^"
L
A aL W, i
. Y!
+ K! 2
' " KD! 2 L " . & )@ ;L ' U %" C. ^ &
& KD G &
" D.
%" 3 6!
+ ) )Q C60T
)
.(
0 A 3 K! 2
).
L
Melia azedarach
' 6 3"
(Meliaceae
J DB KD. K %" $^ F Z @Q 6%P & 6<" %" $+ . $ B
+
+& i+
W ,D;! $D[6T
n D.
)
(
9 DM AP D j $ D, 3 &
K. A" " L *F q " G,% H f0 N+
DL 9 % 'r &
D%" K 2 " ^ '
;2 ' U %"
+ 6B"
.
$D @ 3 7 D KD! 2
)
Morus alba
L.
' 6 3"
Moraceae
(
D%" /& Di+ $ B G6!
K. K
K. AP ! s@Q 'r &
D1 & l `% @+ ' ;2 C6<
DQ& /)
%"
*F G,% L H A"&" 9 ,^"
+ ' 6+
)
.(
&
RL&r A @ $ @ 3 7 & 0 A 3 K! 2
$Dta KO< [+ & L
7 D> AP fD0 N+ DO." )DF &
DB E% E6. $\ &
AP
)+ &
%" K (!
F K0>
1 Y! 3" L
AP E6.
& X ! ?L A B ( . L
?DL & X ! ?L 6-
E6D@j
'3 D% & 7"GD6* D. *!P F K0>
1
&
*DF DL
R6
AP )F $@6.
D & $D.
7")L D + c %" . W,< - L
$+ 7 >
62
.
RL&r E " 3" b)L
#
9)+ 9)+ E66O
$ DL
*Q
E6aN
& )F A"G6+ 1 %
3" ' U %" .
+ K! 2
S."&
$\
.
uB F E6
DB O." K. m . + L
)
X DU "
l [^ & l X U " K@ X U " #C
(
$D+ B E% &
#)DF .
K! 2 K.
9)+ E " va K. A" . K
"
&
DB DO." DL
)DF
!P
R6 f0 N+ E6@% " *
G,% H `% @+
)+ & $@6.
"
9 a1"
.
' \ (
'3")!"
62
& L
#
*DF G,D% H B K! 2
A D 3
@ 3 7 & 0
D
;. $
D
6 & A
D
D% G
9
=
DH
Downloaded from jcpp.iut.ac.ir at 13:57 IRDT on Wednesday May 3rd 2017
-
,
h6
2/13 ( 4 % 0 5
./ 0 1
h16
=
MB%
)
.
#
( 4
ED ( '
# %
J
:
M9 N L
)
2
(
Q N L :
)
i
(
6 N L :
)
Q
(
Q RS
)
(
.(
GDDD,%
)DDF / DD !" )*DD + $DD%&
' (DD !" s
DD
.
DDO."
D
'3")!"
2
DB CD X DU " C+ F K! 2 & E " ')F
6
)
3"
KB F E )@0. p ! E6+3 o[%
Da1 DL
(
KD@ X DU " #
B
)
E6 E6+3 o[% 3"
w . E
l L
(
l X U " &
)! . B l [^ &
.
'3")D!"
D*Q & l D D[^
D62
6+ W *! & )F / !" B K@ . a1 & 3" +
& ED " E6(!
)!)F ' U %" [^ K,% T+ " . ")i+
)
C8F
.(
'3")!"
62
KD06+ 3" ' U D%" D. L
D + & )D@0. l )D+ DL
$! a B %
)
^ .
$06+
+
(
)DF / D !"
.
)D@0. A D B
$D%)@L SD."& 3" ' U D%" . & @% x@% `6F va . X U "
)
y - q6 K[."
(
)!)F K,% T+
.
K.
3" ' U D%" . K `6 E "
`6F
@% x@%
dD " o[D% D DB p D! 3" `6F ")i+
&
?L
3" E6@j
E.
d " o[% B
'3")!"
B X U " &
62
3" ' U %" .
3 9 +
)F K,% T+
.
H = B (Tg –Tg )
h
:
# B X U "
B
:
+ `;I . B $i " K0>
#
Tg
:
E. `6F )>
B
&
Tg
:
p ! `6F )>
B
.
' " 3" ' U D%" . A B E%
#An :D;+ )D6 z
D+ DL
$DJ s
KJ T+ G,% H A" 2 & A" { !
=
9 D%
K. K F 2
)+P %
.
D*!P D A D+3 3" A B E% 6O+
)!)F K 2 Y! s
KJ T+
.
A B E% K
" +
K.
N+ C n
'3")D!" & 3" D,! D% fD0
S6DT+
D62
)DF ' U %" AP E% E6aN " . B
.
S6DT+ & ED "
'3")!" B K@ A +" 6
D 3 9 + va . s|% & )F
62
)F K,% T+ AP $, i E%
)
=
.(
B [^
=
B S6T+
/
$ )1
B E%
=
B [^
×
)F
B
ED " &
%" $ & U + ")i+ f0 N+ A B )F
$D @ 3 7 & 0 A 3 A B " . ")i+
WD, i
DY!
)F K 2
)
=
.(
&)I C
=
'3")!" B
)!)DF
D62
K
=
& $D @ 3 7 D KD! 2 KD. m . + B
=
DB
E6. $@% K@+" . 0 A 3 K! 2 K. d0O +
)D! . 9 %
.
A 8+ ')F A B
g 3 s
KJ T+ f0 N+ L
'3")!" &
F" $! ;8 W ,;! $@%
A D8+ DL A D B
62
K.
)DF / D !" $ M W_+ 7 >
.
3" A D B D K0D>
9&)Q # ( )8
A D8+ KD. KDQ D. & E6DF + L 6D;+ & L
'3")!"
D62
)
D. 6B K6DF I # " D< .
G,D% DH D & $D A
G a +
(
K. +" . 7& U +
7 D A B E6. K0> S% + J
&)I $ @ 3
/
0 A 3 &
. +
.
A B
q "
KD. $D%&
' (D !" s
KJ T+ G,% H ')F
CD6<
S6DT+ A ;8
)+
#
D6.P DY! 3" K. D + WD, i DL
f01 9 @ #$L
& 3 L L
...
)D! . KD
&
.
E6D.
'3")!" O."
B L ')F
62
)
D[^ & KD@ X U " #C X U "
l
(
AP E% &
"G " / ! 3" ' U %" .
Excel
A 6% 2 X" !"
L
' %
$D[B
)
Linear
(
)D@j #
KD0aQ
"
)
Polynomial
(
#
$ Da!
)
Exponential
(
$a
DD(< #
)
Logarithmic
(
$!" DD &
)
Power
(
Downloaded from jcpp.iut.ac.ir at 13:57 IRDT on Wednesday May 3rd 2017
/
!"
/
# $%
&'( !"
/
)*+*
=
)F K 2
fD0 N+ E6@D% & DO." DB )DF 1 D%
F K,% T+
.
9)+ K^ % $[6T+ )F G6< !P " . f0 N+ 7 O< [+
L
$a
D(< #$ Da! CDq+
)O + )F $@T@+
)
(
#
Lundqvist
)
(
&
Richarde family
)
(
)!)F R +3P
.
KD< O+ D *!
K. $a
(<
O+ E *. A" @1
K^ D% S6T+ )F K,% T+ " . K<
' " ." .
& )DF KD 2 DY! DB E% K. m . + L
DO." )DF 1 D% E6D6O " . G6! \ I RL&r E " . @.
'3")!" f0 N+
$D @ 3 7 D & 0 A 3 K! 2 & ')F
62
)F ' U %" $a
(< K< O+ 3"
.
K! 2 )F R@ "&
+" c %" . L
B O."
L
.
K
)!)F G6< !P K!n % )F
1 % E6(! 6+ K06%&
)
h
(
E "
K[."
:
AGR
=
a-b/t
K[."
)
(
AGR
K!n % )F 1 % E6(! 6+
)
(Annual Growth Rate
.
`;I
06+
$
9 % +
a
:
w G.
B )O. E
)
mm
(
#
b
:
vj
DB )DO. E
)
mm
(
w G. )1 # B [^ & X U " O." E6. 3" #
A" @1 K.
a
vj )1 &
K.
A" @1
b
F $+ K 2 Y!
.
t
:
62 '3")!" E6. $! +3 ' &
L
)
$! D+3 ' & d6iT E "
%" ')F K 2 Y! 9 %
.(
E6(! D6+ ~ K[." 3" ' U %" .
K!n % )F
$! D+3 '3 D.
KD! 2 DL " D. D. vD 9 D%
F $+ K,% T+
.
j W 1
E6D6, ` " D\ #$! 6D% 2 7n DO+
)
R
(
D[B E6(! D6+ &
")! D%"
)
MSE
(
$DD @ 3 7 D & D0 A D 3 KD! 2 & " D.
K.
9&")Q `6
&
')F K•" "
)D!"
.
D0 A D 3 KD! 2
" E6D. A 6% 2 ` " \ E n .
DB ED% & CD X DU
KD0aQ )DD@j SD."&
"
)
/
=
=
R
(
$D[B #
)
/
=
=
R
(
&
$!"
)
/
=
=
R
(
SD."& DB E% & K@ X U " E6. &
KD0aQ )@j
"
)
/
=
=
R
(
$!" D #
)
/
=
=
R
(
$a
D(< #
)
/
=
=
R
(
$[B &
)
/
=
=
R
(
ED% & l [^ E6. &
$!" K[."
)
h
/
=
=
R
(
)
2 &P .
.
A aL
J
9&)DQ 3" K
)
(
$D+ uND +
DO." E6D. )DF .
'3")!"
K. 0 A 3 B ')F
62
& K D;."& D6€ + A" @1
KD. *!P E%
& n D. W ,D;! E6D6, ` D\ Ci D;+ D6€ + A" D@1
@O+
$
$! 6% 2 g." AP ")i+ E 6. K
" Q&
"
U " E6. ')F &P .
$+ ') B E% & C X
F
)
9&)DQ
.(
X DU " E6D. A 6% 2 ` " \ E n . $ @ 3 7 K! 2
)D@j S."& B E% & C
KD0aQ
"
)
h
/
=
=
R
(
$D[B #
)
Vh
/
=
=
R
(
$ a! &
)
V
/
=
=
R
(
ED% & l D [^ E6. &
$!" S."&
)
Vh
/
=
=
R
(
$ a! #
)
VV
/
=
=
R
(
KD0aQ )@j #
"
)
V
/
=
=
R
(
$DD[B &
)
V
/
=
=
R
(
)DD
2 &P DD.
.
` DD\
CD> I SD."& KD60 B E% & K@ X U " E6. A 6% 2
/
=
-
=
/
=
=
R
.
K
)+P %
.
'3")!" O." E6. $ @ 3 7
DB C X U " ')F
62
K. l [^ &
A" @1
6€ +
D6€ + A" @1 K. *!P E% & K ;."& L
` \ #Ci ;+
$@O+ & n . E66,
" DQ&
"
$< DI
KD
K. K@ X U " E6,, ` \ ")i+
ED% & K D;."& D6€ + A" @1
K.
%" E6 Ci ;+ 6€ + A" @1
)
9&)Q
.(
K. K! 2 & L
` D\ A"GD6+ E D a $D @ 3 7 'r &
A D B KD@ X U " K. m . + E% &
B O." E6. A 6% 2
%"
.
c L
K. A
KB F g[^ 'r &
DB l D $@6 D DL
KD. G,D% DH A B
")*(! 7 60a1 3" $8
D, 3 DY@+
KB DF )DF 9 D @ D & D*!P 3 D%
3"
62 DD0Q D*Q DL
*F 7"G6* & )+P &
" . $< a I" aI"G+
D%"
B K@ X U " & E " 3"
3" $O. D # *!P $O6,J )F . '&_1
a1
$+ G6! A B
")*(! &
F" 7 60
)F .
)
&
.(
$01
E " ?-
#$D @ 3 7 D & D0 A 3 K! 2& L K
9)D+ $( D;."& ` " \ E n .
WD,< - #CD> I gD." & DL
K0aQ )@j X ! g." K. m . +
$ a! & $[B # "
)
D6- $O." D
$a
(< g." 3"
(
R6 " . Q& E " . .
.
)DF A"GD6+ $@6
Downloaded from jcpp.iut.ac.ir at 13:57 IRDT on Wednesday May 3rd 2017
-
,
h6
2/13 ( 4 % 0 5
./ 0 1
h16
=
X
)
.
:
MSE
;
R
F F
J Y
MC H
)
lMT1U V1
x
(
6 N L :M9 N L l
' 1
-
Q RS
)
l 1U V1
y
(
./ 0 1 (
R
2
MSE
b
a
9)+
)
K< O+
(
K< O+ X !
./
=
V
/
h
/
V
h
/
y =
h
/
x +
h
/
V
$[B
hV
/
=
“
h
/
=
-
V
/
y =
V
/
Ln (x) –
h
/
=
$a
(<
/
=
“
/
/
=
y =
/
=
x +
/
x +
=
/
" K0aQ )@j
E% & C X U "
/
=
“
/
=
/
y =
/
x
/
=
$!"
hh
/
=
“
h
/
=
h
/
=V
y =
h
/
=V
e
h
/
=
x
$ a!
/
=
/
/
V
/
y =
V
/
x +
h
/
$[B
V
/
=
“
V
/
-
h
/
h=
y =
h
/
h=
Ln (x) –
V
/
$a
(<
/
=
“
V
/
/
-
y = -
h
/
x +
V
/
x –
h=
/
" K0aQ )@j
& K@ X U "
E%
/
=
“
V
/
=
/
y =
/
x
V
/
=
$!"
/
=
“
/
=
VV
/
y =
VV
/
e
/
=
x
$ a!
V
/
=
/
=
h
/
-
VV
/
V
y =
VVV
/
V
x –
h
/
V
$[B
V
/
=
“
V
/
h
-
/
y =
/
Ln (x) –
V
/
h
$a
(<
V
/
=
“
h
/
-
y = -
h h
/
x
2
+
==
/
x –
V
/
h
" K0aQ )@j
E%& l [^
h
/
=
“
/
=
/
=
y =
=
/
=
x
/
$!"
V
/
=
“
= h
/
V
/
y =
V
/
e
= h
/
=
x
$ a!
X
;
.
:
MSE
;
R
F F
J Y
MC H
)
lMT1U V1
x
(
6 N L :M9 N L l ' 1
-
Q RS
)
l 1U V1
y
(
16
(
R
2
MSE
b
a
9)+
)
K< O+
(
K< O+ X !
Vh
/
=
/
/
h
h
/
y
=
h
/
x +
/
h
$[B
=
/
=
“
/
/
V
y =
/
V
Ln (x) +
/
(<
$a
h
/
=
“
/
=
/
y =
=
/
x –
/
x +
/
h
K0aQ )@j
"
E% & C X U "
/
=
“
Vh
V
/
=
y =
V
/
=
x
Vh
/
=
$!"
V
/
=
“
=
=
/
=
y =
=
/
=
e
=
x
a!
$
/
=
h
/
h
/
/
y =
/
x +
h
/
$[B
=
/
=
“
=h
/
V=
/
y =
V=
/
Ln (x) +
=h
/
(<
$a
/
=
“
V
/
V
/
=
-
y =
/
=
-
x +
V
/
V
x +
VV
/
=
K0aQ )@j
"
E% & K@ X U "
/
=
“
h
/
=
h
/
y =
h
/
x
h
/
=
$!"
/
=
“
X
=
/
=
/
y =
/
e
=
/
=
x
!
a
$
V
/
=
h
/
V
=
/
h
h
/
y =
h
/
x +
=
/
h
$[B
/
=
“
h
/
=
-
/
h
y =
/
h
Ln (x) –
h
/
=
(<
$a
V
/
=
“
=h
/
h
hVV
/
=
y =
hVV
/
=
x +
=h
/
h
x +
/
K0aQ )@j
"
E% & l [^
Vh
/
=
“
V h
/
=
/
y =
/
x
V h
/
=
$!"
VV
/
=
“
/
=
/
VV
y =
/
VV
e
/
=
x
a!
$
Downloaded from jcpp.iut.ac.ir at 13:57 IRDT on Wednesday May 3rd 2017
/
!"
/
# $%
&'( !"
/
)*+*
=
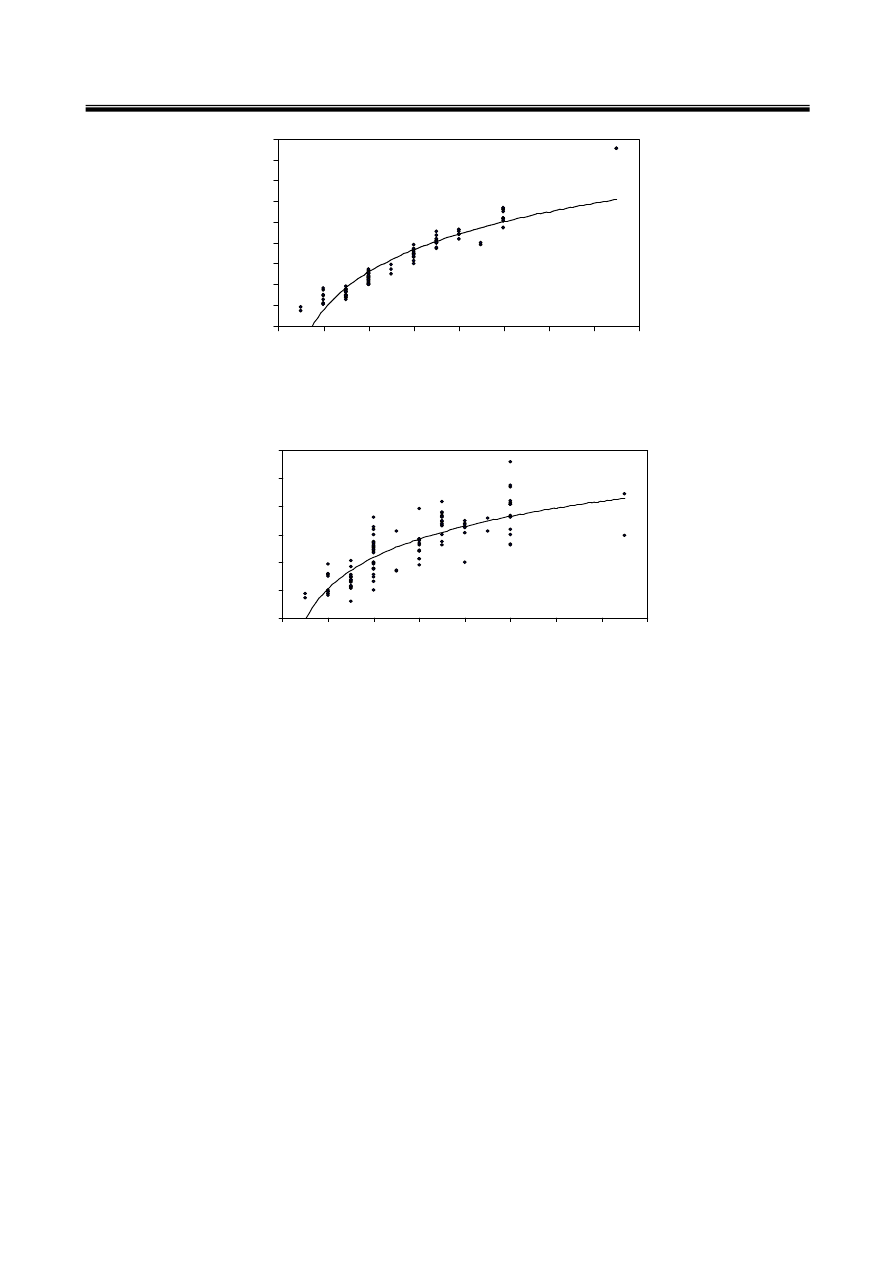
y = 264.37Ln(x) - 105.98
R
2
= 0.8664
0
100
200
300
400
500
600
700
800
900
0
2
4
6
8
10
12
14
16
(
)
(
)
MB%
)
.
./ 0 1 ( ED ( F N L F $1 O
J Y ( $
y = 80.185Ln(x) - 1.9574
R
2
= 0.6682
0
50
100
150
200
250
300
0
2
4
6
8
10
12
14
16
(
)
(
)
MB%
;
.
./ 0 1 ( ED ( F
6 N L F $1 O
J Y ( $
'3")D!" O."
9)D+ #fD0 N+ E6@D% ')DF
D62
gD." & DL
K. $a
(<
)+ A" @1
9
R6 `% @+ & ') G2 . L
DL $D@6.
)!)F Z N !" K! 2 &
.
X U " #C X U " )F 9)+ & (<"
KD@
?L &
$08DF K. $ @ 3 7 & 0 A 3 A B l [^ E6@j
K0aQ )@j & $[B g." 3" ' U %" . K
%"
"
&)DI &
R6 $!"
KD. $< D,^ CD. ^ & o6TD> $@6.
)D+P )DL" N! D%
K.
J
9)+ E " K
K. A B E% R "G " . L
E6@D% 'rD &
n DD.
)
&)DDI
n DD. & 9 DD%
(
R6DD
$ n DD. 6DD;. $DD@6.
)
Overestimate
(
S " DDF W_Da1 KD )DD! " DB DO." 3"
ED% AP O." E6@j . $! B $O6,J
ED " &
")D! DQ&
9)+
R6 *Q g." & L
)F
(<" $@6.
KD. A D B ED "
)@ ;6! 9 ,^ C. ^ $a01 ‚ T<
)
.(
3"
$DB . K. X Q . $ J
&
6O\& K. KQ . $a
(< 9)+ #K. + 7n i+ & 7 i6iT
9)D+ A" D@1 KD. l [^ & K@ X U " #C X U " )F
(<"
R6 *Q 9 ,^ C. ^
fD0 N+ E6@D% O." E " )F $@6.
F $+ K 2 Y!
)
,
&
(
.
C8F
L
)
-
(
&
)
-
(
K.
6
@T@+ ')@L A ! `
$
% 2 K."
6
(< A
a
$
.6
DO." E
3 KD! 2 & ED% & )DF f0 N+
3 7 D & D0 A D
D @
$
+
$
)F .
.
K. $a
(< 7n O+ 3" ' U %" .
KD! 2 L " . ')+P %
'3")!" O." )F A"G6+
')F
62
)
" #C X U "
D[^ & K@ X U
l
(
E6@%
=
#
&
=
R6 9 %
)!)DF $@6.
)
9&)DQ
.(
R6
E6@% C^")I O." $@6.
=
&
$DO^"& DO." KD. 9 %
)@ ;L v G! 6;. E6@% E " A B
.
K!n D% )F 1 %
Downloaded from jcpp.iut.ac.ir at 13:57 IRDT on Wednesday May 3rd 2017
-
,
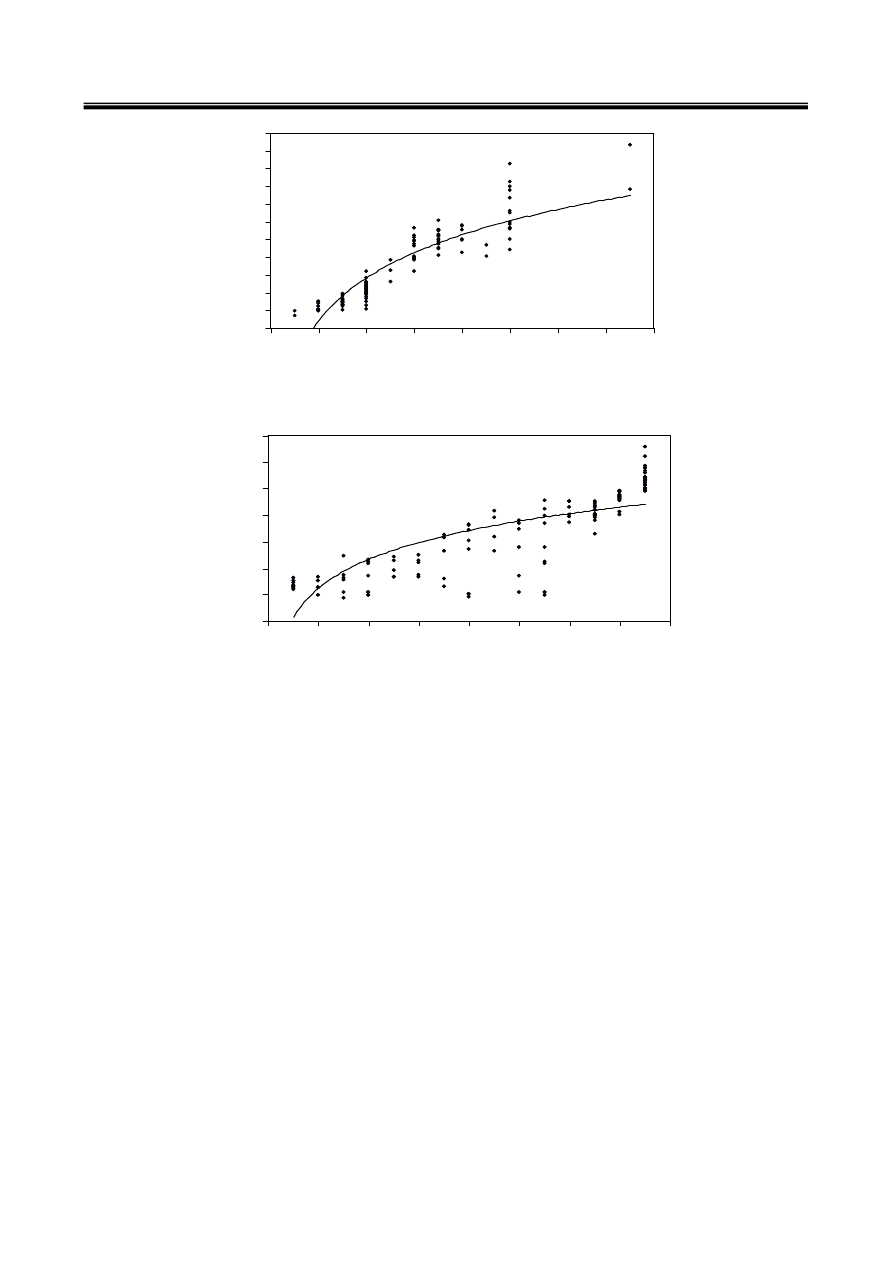
h6
2/13 ( 4 % 0 5
./ 0 1
h16
=
y = 352.96Ln(x) - 204.45
R
2
= 0.8008
0
100
200
300
400
500
600
700
800
900
1000
1100
0
2
4
6
8
10
12
14
16
(
)
(
)
MB%
*
.
./ 0 1 ( ED ( F Q RS F $1 O
J Y ( $
y = 157.61Ln(x) + 14.326
R
2
= 0.6027
0
100
200
300
400
500
600
700
0
2
4
6
8
10
12
14
16
(
)
(
)
B%
M
?
.
16
( ED ( F N L F $1 O
J Y ( $
E% 0 A 3 B C X U "
$D "G " )!& $(< %
E6@% +" K F"
h
-
AP 3" sD $D<& KD RL D $(< D%
$+ $
) R "G " K. & W" ) +
" 2
.
KD@ X U " )F 1 %
E%
& R "G " $(< %
K. AP 3" s
J
RL D KD. & $D0
+" " 2 $+
KDYI_+ CD. ^ R "G " l [^ )F 1 %
" "
K.
E% 'r &
$+ A ! $(< %
$,D;! J AP 3" s $<& )L
$+ RL K. &
" 2
.
K.
J
$+ $0
ED% R "G " . U2 A"
&)I
9 D% K.
,;! K! 2 E " )F 1 % $(< %
DL
K6<&"
$+ A ! R "G " )F
)L
.
K.
J
DO." )DF 1 % $0
'3")!"
D. $ @ 3 7 B l [^ & K@ X U " ')F
62
$+ R "G " E% R "G "
v )@j L ).
3 D. & uND + KU^&
E6@%
-
?D j KD. KD@ X DU " )DF 1 D% $(< D%
$+
$+ K
B
)+ „ % K. m . + )!"
)F . $ L
)F K
6…z T " K@ $< J
$+ " ^
D[^ )F 1 % K " j )@L
$+ A ! " $O % $ "G " )!& A @j ?L E% E " l
)L
&
")D! $DaY@+ )D!& DB CD X U " )F 1 % +"
$+ ')L + f0 N+ E6@% AP R "G " & RL
F
)
9&)DQ
.(
A aL
9&")Q K
J
&
$+ A !
KD! 2 & DL )DL
. K; i+ E% R "G " . l [^ )F 1 %
)DF 1 %
ED " KD. AP D01 ) DF KD %" 6. K@ X U " & C X U "
&)DI D ED% R "GD " D. K )F . C6<
A D B $(< D%
E;+
')DF vD G! B $1 U " & $< J )F q ")I K.
)D!"
$< I
;2 & $,! Q )F K
?DL DB l
KD+" " A D@j
"
)
.(
Downloaded from jcpp.iut.ac.ir at 13:57 IRDT on Wednesday May 3rd 2017
/
!"
/
# $%
&'( !"
/
)*+*
=
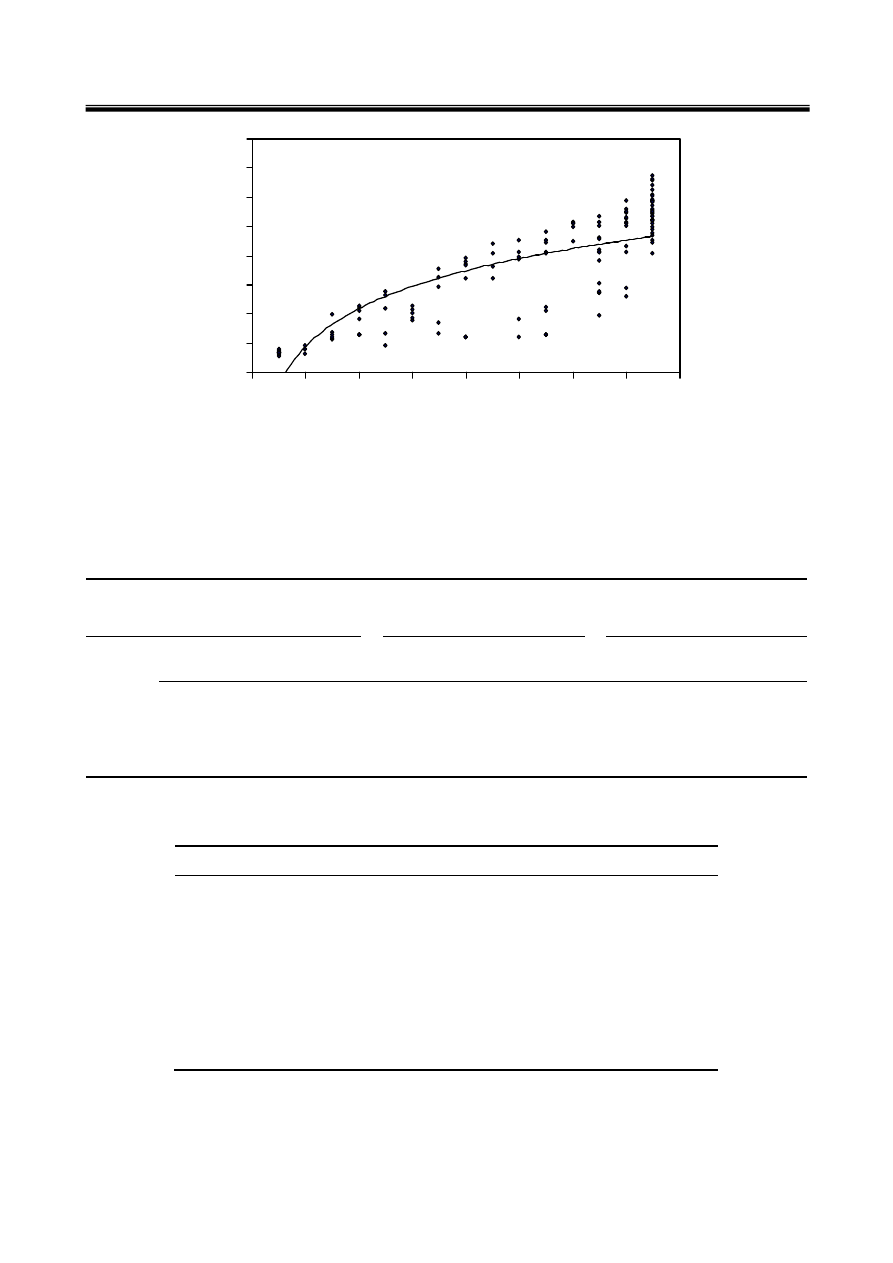
y = 186.91Ln(x) - 40.284
R
2
= 0.6472
0
100
200
300
400
500
600
700
800
0
2
4
6
8
10
12
14
16
(
)
(
)
MB%
d
.
16
( ED ( F Q RS F $1 O
J Y ( $
X
*
.
, -
F 6 ( Q RS
6 N L :M9 N L 6
)`
:
)d
*`
16
./ 0 1 (
$1 O # % \
m
l [^
)
+
(
K@ X U "
)
+
(
C X U "
)
+
(
K! 2
=
9 %
9 %
=
9 %
=
9 %
9 %
=
9 %
=
9 %
9 %
=
9 %
/
/
V
/
V
/
/
h
/
/
V
=h
/
=
/
0 A 3
/
/
=
/
/
=
/
h
/
=
/
/
VV
/
$ @ 3 7
X
?
.
% E
F O
' # % 7
Q RS
6 N L :M9 N L
;
./ 0 1 ED ( ( 7B
l [^
)
mm
(
K@ X U "
)
mm
(
C X U "
)
mm
(
E%
==
=
=
-
=
=
V =
V
-
==
=
-
V
=
=
h
-
=
=
=
=
-
h
V
V
h
-
=
h
V
V
-
Downloaded from jcpp.iut.ac.ir at 13:57 IRDT on Wednesday May 3rd 2017
-
,
h6
2/13 ( 4 % 0 5
./ 0 1
h16
=V
X
d
.
' # % 7
Q RS
6 N L :M9 N L
% E
F O
;
16
ED ( ( 7B
l [^
)
mm
(
K@ X U "
)
mm
(
C X U "
)
mm
(
E%
V=
==
-
=
V
-
=
=
=
-
=
V=
h
-
h=
V
=
-
h
V
-
=
h=
=
h==
-
AP
DL K %" E " %" uN + 9&")Q & x ! 3" Kj
KD. $ n D. W ,;! )F 1 % $ @ 3 7 & 0 A 3 K! 2 &
E6@D% D C^")DI l D KOD% &
;2 Y! 3" 'r &
-
*. $@O G,% )F 9 M AP 3& . &
*{ K )! " $(< %
A ;. &
uN +
K. &
%"
J
D W ,D;! A B &GQ $0
$D+ Z ;I K. G,% H )F
)D@ P
.
9)D+ 3" ' U D%"
& DL
)DF
D(<" A D $Da D( $! D6. KD. & $\ g."
" A D8+" ED " G,D% DH A" )+ & A I" J K. $ @ 3 A B
$+
E6@D% " DB fD0 N+ DO." )DF 1 D% KD )L
f0 N+
R6
o6T>
M & )@@ $@6.
$O^"& &
H 3"
)@DF . K F" ')@ P ')F $I" J G,%
.
9)D+ ED "
gD." & DL
CDDq+ G,DD% DDH DDL "G " / DD! ' U DD%" DD60. ^
CAD
(Computer Aided Design software)
EDD " KDD. & )DD! " "
< D 6
7 > K. f0 N+ E6@% B )F 66€ `6
$
K6,F G6!
M &
$+ 3 %
F
)
.(
$ D 7 1_J" E F"
B O." . m , "
)
l D D[^ & KD@ X DU " #C X U "
(
$+
# Da60 & 86+ ,*. #" L $2 <P Z Q A
9)+ " . )!"
& E. Z Q K,% T+
...
S6T+
F K 2 K.
*F L
)
(
.
1_J" E F" . $ J 3"
A 8+" A B O." K. m . + 7
d6^ K,% T+
K@ GL
K+ ! . G6< !P # L
Z D0[+ $
)D+ L
9 %
?L" D
*F ") G,% L H
" b)L . ')@ P L
$+
F
.
9)+ E " va .
)DF 1 D% KDj A D@j gD." & L
A D8+ AP D & ' U %" A 8+" )F . 3 $ B
D. $ DL
H
D6O^ + & 3 .
& g D% G,D% RDF 3 D6! KD $ DL
%" K6> C. ^ F $+ c ;I"
.
?L
D+ E6@j
A D8+ DF K. K6> )F ? A B
L DH D. $ DL
. Cq+ &)T+
' 6 & L " <
A . 6B L&
] 0DF &
L
. )L" B K6Q C. ^
.
Y 6
#( L1 (
1. Brewer, J. A., P. Y. Burns and Q. V. Cao. 1985. Short term Projection accuracy of Ive asymptotic height–age
curves For Loblolly pine. Forest Science 31: 414–418.
2. Du Toit, S. H. C. 1979. Analysis of growth curves. Ph.D. Thesis, University of South Africa, Pretoria, South Africa.
3. Fox, J., H. Bi and P. Ades. 2007. Spatial dependence and individual-tree growth models II. Modeling spatial
dependence, Forest Ecology and Management 245: 20–30.
4. Gerhold, H. D., N. L. Lacasse and W. W. Andel. 1993. Street tree fact sheets. University Park, The Pennsylvania
State University. AGRS-056.
5. Harrison N. A., E. Boa and M. L. Carpio. 2003. Characterization of phytoplasmas detected in Chinaberry trees with
symptoms of leaf yellowing and decline in Bolivia. Plant Pathology 52: 147-157.
6. Hickey M. and C. J. King. 1981. Moraceae, 100 families of flowering plants. Cambridge University Press, London.
Downloaded from jcpp.iut.ac.ir at 13:57 IRDT on Wednesday May 3rd 2017
/
!"
/
# $%
&'( !"
/
)*+*
=h
7. http://www.learner.org/jnorth/tm/leaf/HowOld.html
8. Ishii, H., J. P. Clement and D. C. Shawc. 2000. Branch growth and crown form in old coastal Douglas-fir, Forest
Ecology and Management 131: 81-91.
9. Jalota, R. K., and K. K. Sangha. 2000. Comparative ecological–economic analysis of growth performance of exotic
Eucalyptus tereticornis and indigenous Dalbergia sissoo in mono-culture plantations. Ecological Economics 33:
487–495.
10. Joffe, P. 1993. The gardener’s guide to South African plants. Tafelberg-Uitgewers Beperk, CapeTown.
11. Kirsten, K. E. and L. Meyer. 1992. Keith Kirsten’s complete garden manual for South Africa. Human and Rousseau,
Cape Town.
12. Larsen, F. K. and P. Kristoffersen. 2002. Tilia’s physical dimensions over time. Journal of Arboriculture 25: 209–
213.
13. Peper, P. J., E. G. Mc Pherson and S. M. Mori. 2001a. Predictive equations for dimensions and leaf area of coastal
southern California street trees. Journal of Arboriculture 27: 169–181
14. Peper, P. J., E. G. Mc Pherson and S. M. Mori. 2001b. Equations for predicting diameter, height, crown width and
leaf area Of San Joaquin Valley street trees. Journal of Arboriculture 27: 306–317.
15. Pukkala, T., T. Kolstrom and J. Miina. 1994. A method for predicting tree dimensions in Scots pine and Norway
spruce stands. Forest Ecology and Management 65: 123-134.
16. Simard, S. W., and B. J. Zimonick. 2005. Neighborhood size effects on mortality, growth and Crown morphology
of paper birch. Forest Ecology and Management 214: 251–265.
17. Stoffberg, G.H., M. W. van Rooyen, M. J. van der Linde and H. T. Groeneveld. 2008. Predicting the growth in tree
height and crown size of three street tree species in the city of Tshwane. South Africa Urban Forestry and Urban
Greening 7: 259–264.
18. Teimoori, R., S. Roostaee, A. Akbarizamaneh and M. Ahadinejad. 2010. The evaluation of spatio-temporal
suitability of urban parks using GIS (a case study of area no. 2 neighborhood parks of Tabriz municipality).
Itanian Jornal of Geographic Space 10: 137-168. (In Farsi).
19. Wyckoff, P. H., and J. S. Clark. 2005. Tree growth prediction using size and exposed crown area. Canadian Journal
of Forest Research 35: 13-20.
20. Zhanga, L., H. Bi, P. F. Chenga and C. J. Davis. 2004. Modeling spatial variation in tree diameter–height
relationships. Forest Ecology and Management 189: 317–329.
Downloaded from jcpp.iut.ac.ir at 13:57 IRDT on Wednesday May 3rd 2017