Financial Market

Derivatives Market – Vanilla Options – Call option

HOLDER

WRITER

Participans:

The deal:

For a specific period of time

HOLDER

will have a

RIGHT to buy

some underling security for a price specified

today.

Options’ features:

when the maturity comes, holder has the

right to demand from option’s writer to sell him particular security at price

specified in contract.

WRITER

will have an

OBLIGATION

to

deliver

the underlying security.

Strike (Exercise price) (K) = price at which the underlying transaction will occur

upon exercise.

Expiration date (Maturity) (T) = the day when the options expiry.

Multiplier (N) = the quantity of the underlying asset.

Underlying security = what security is going to be traded.

CALL option

=

holder gets the

right to buy

=

Financial Market

Derivatives Market – Vanilla Options – Call option

Today

Maturity

Holder

gets

the right

for a future transaction.

Holder can (but doesn’t have to)

finalize transaction.

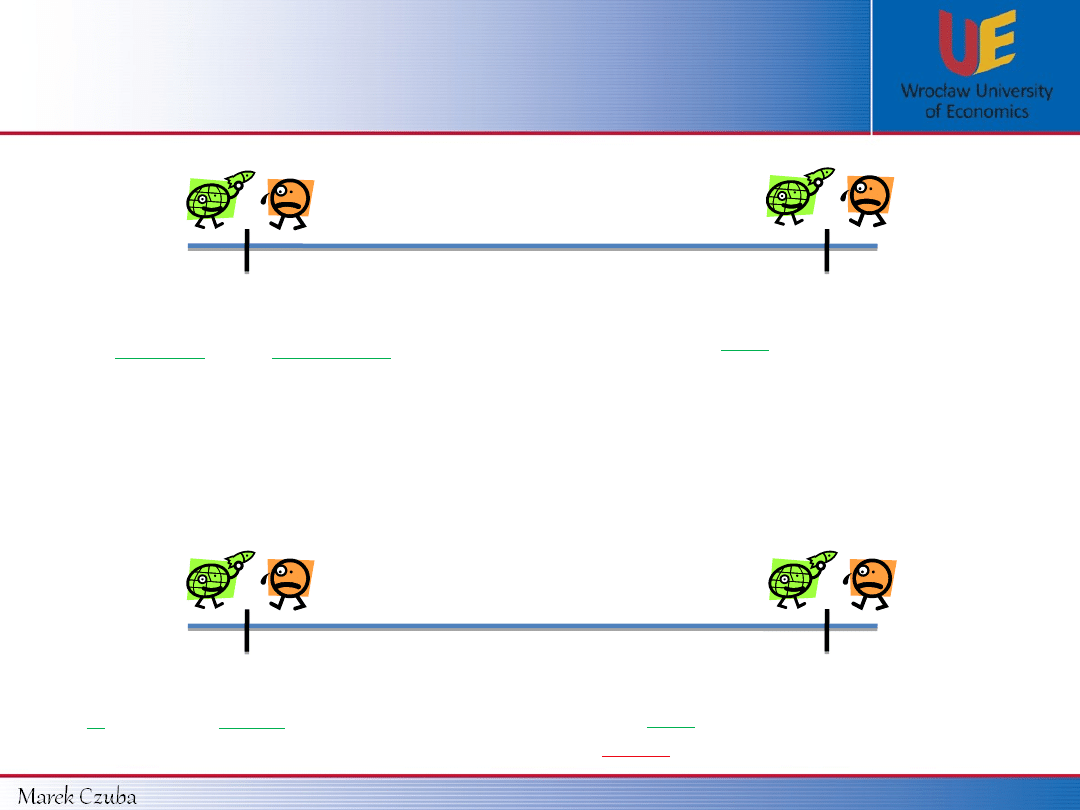
Example 1:

A is signing a contract with B specifying that in a one year from now he will have
the right to buy 1 stock of X company for a 10$ (the price specified in the
contract).

Today

After 1 year

A

gets the

right

to buying 1

stock of X company from

B

but

after 1 year.

A can

buy 1 stock of X company.

B must

sell that 1 stock, if

A

will call for

that.

Writer is obliged

to finalize

transaction but

only if holder

calls

for that.

Financial Market

Derivatives Market – Vanilla Options – Call option

Data from example 1:

Will CALL’s holder execute his rights ??

Underlying security = Stock X

N = 1

T = 1 year

K = 10 $

Let’s assume that stock X price after T is going to be:

a) S

T

= 20

$

b) S

T

= 15

$

e) S

T

= 10

$

c) S

T

= 8

$

d) S

T

= 5

$

CALL’s holder has the right to buy stock X for 10 $ (stock X is listed

with higher price at this moment) – Holder executes his right and in

the same moment sells stock X at the market for a higher price.

CALL’s holder will not execute his right while he can buy the same

stock at the market much cheaper. Hence CALL option is worthless.

CALL’s holder will not execute his right while he can buy the same

stock at the market at the same price. Hence CALL option is

worthless.

Financial Market

Derivatives Market – Vanilla Options – Call option

CALL

option

HOLDER

will execute his right

when:

S

T

> K

What will be CALL’s holder payoff (if Strike = 10 $):

a) S

T

= 20

$

b) S

T

= 15

$

e) S

T

= 10

$

c) S

T

= 8

$

d) S

T

= 5

$

CALL’s holder executes his right: he buys stock X for 10 $ from writer.

At the same moment, he sells this security for:

a) 20 $ b) 15 $

a) 10 $ b) 5 $

Payoff:

CALL’s holder will not execute his right, while he can buy the same

stock from market for:

c) 8 $ d) 5 $

c) 0 $

d) 0 $

Payoff:

CALL’s holder will not execute his right, while he can buy the same

stock from market for the same price.

e) 0 $

Payoff:

Financial Market

Derivatives Market – Vanilla Options – Call option

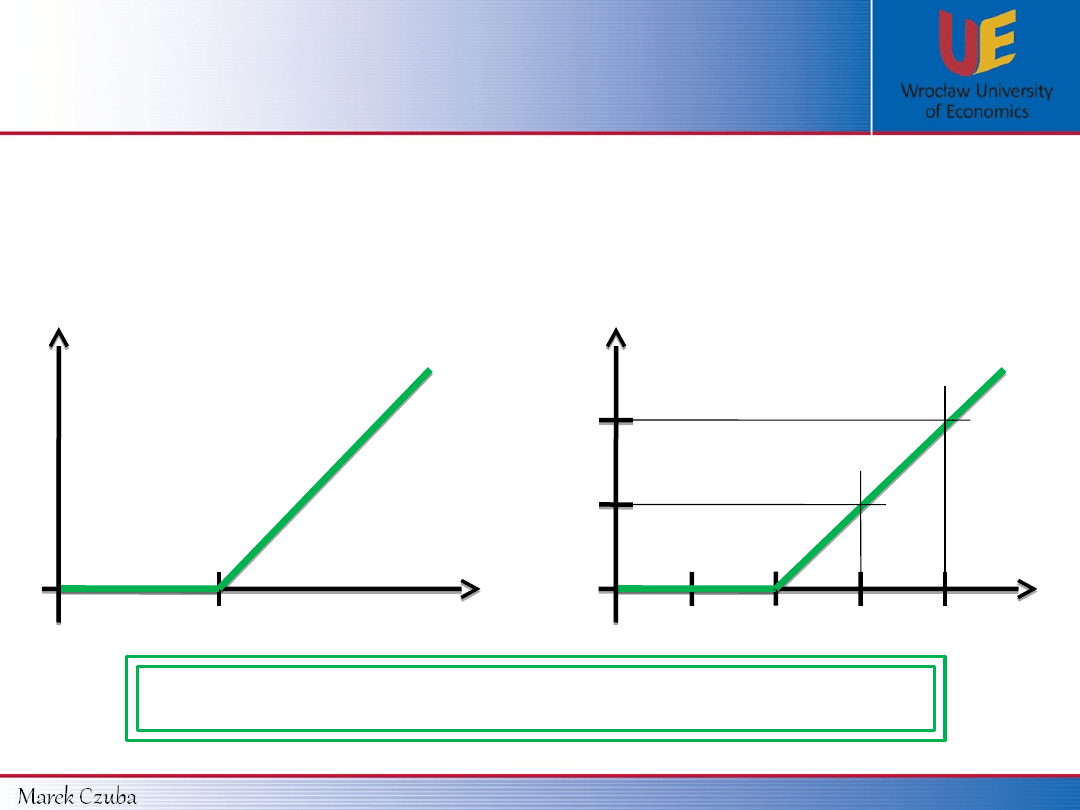
CALL’s

holder

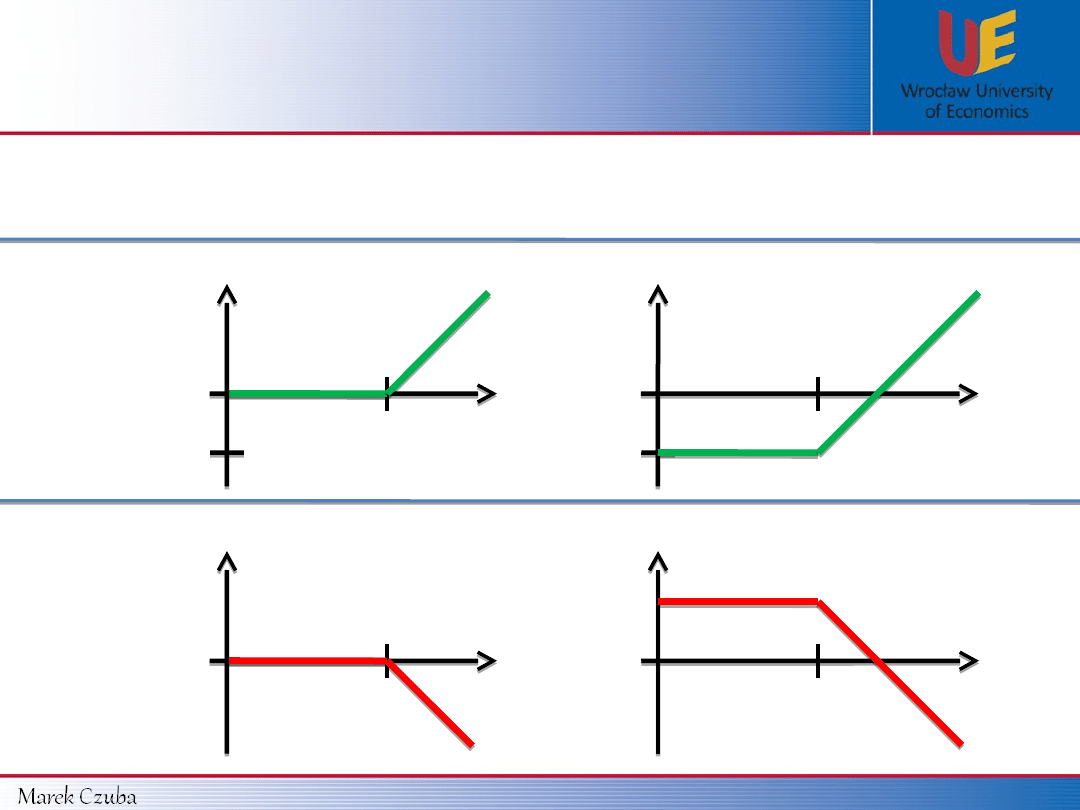
payoff function:

K

0

S

T

Payoff

In general:

10 $

0

S

T

Payoff

Data from example 1 (K = 10 $):

15 $

20 $

5 $

5 $

10 $

MAX(S

T

– K ,

0)

Payoff function for CALL’s

holder

=

Financial Market

Derivatives Market – Vanilla Options – Call option

Data form example 1:

CALL’s

writer

payoff function:

a) S

T

= 20

$

b) S

T

= 15

$

e) S

T

= 10

$

c) S

T

= 8

$

d) S

T

= 5

$

Writer will be asked by the holder to sell the security. Hence, writer

will buy stock X from the market (paying a) 20 $ b) 15 $) and will sell

this stock immediately to holder (asking 10 $).

Writer won’t be called to sell the stock X, while holder will not execute

his right.

c) 0 $

d) 0 $

e) 0 $

Payoff:

a) -10 $b) -5 $

Payoff:

Underlying security = Stock X

N = 1

T = 1 year

K = 10 $

Let’s assume that stock X price after T is going to be:

Underlying security = Stock X

N = 1

T = 1 year

K = 10 $

Financial Market

Derivatives Market – Vanilla Options – Call option

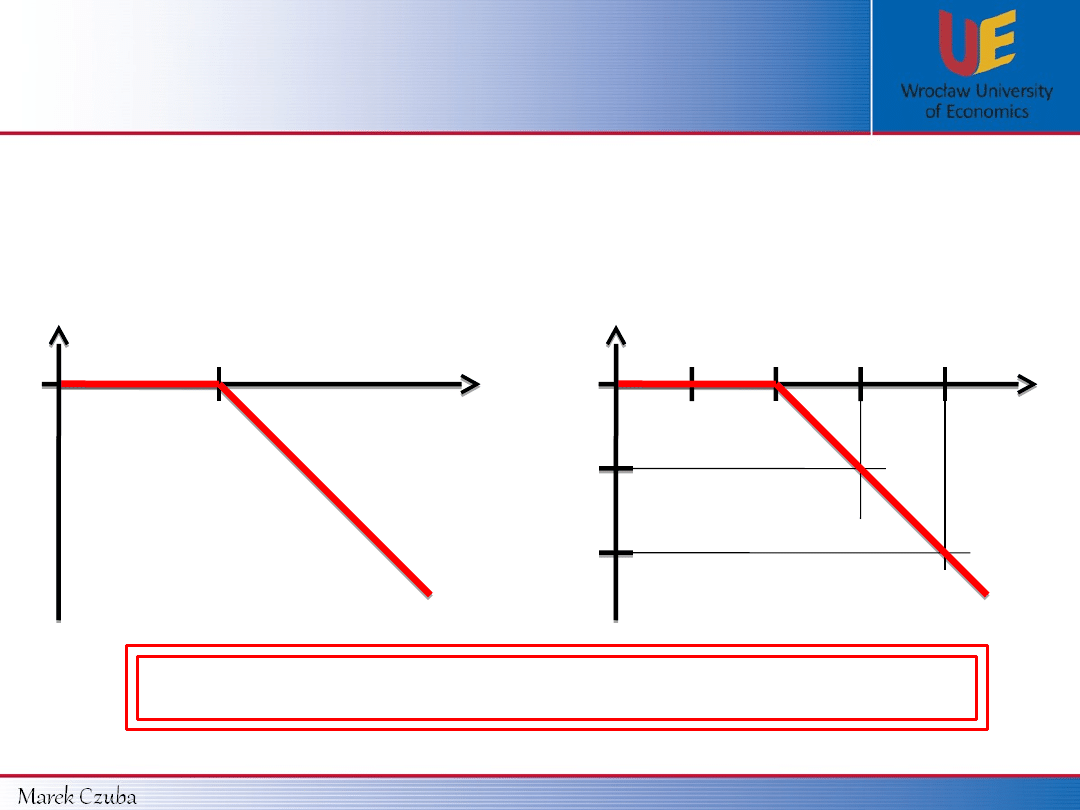
K

0

S

T

Payoff

10 $

0

S

T

Payoff

15 $

20 $

5 $

- 5 $

- 10 $

- MAX(S

T

– K ,

0)

CALL’s

writer

payoff function:

In general:

Data from example 1 (K = 10 $):

Payoff function for CALL’s

writer

=

Financial Market

Derivatives Market – Vanilla Options – Call option

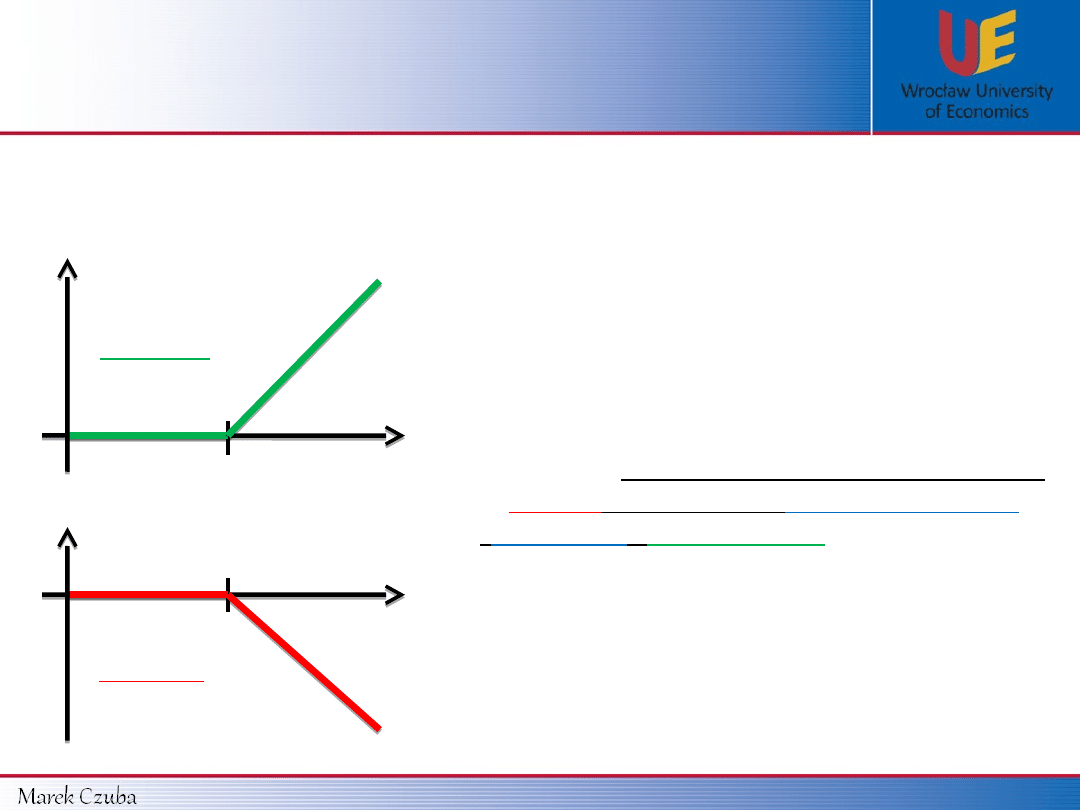
Holder

 

Writer

K

0

S

T

Payoff

K

0

S

T

Payoff

HOLDER

WRITER

Holder:

has

nothing to lose

– can

make a

big profit.

This is why

when the contract is signed

writer

demands a

single payment

(

Premium

)

from holder

for giving him the

right to buy some security in the future for a

price specified today.

This is definitely unfair.

c

–

CALL

option price

(Premium, which needs to be paid by the holder

to the writer for obtaining the right for a future

transaction).

Writer:

he is

risking a lot

- got

nothing to

gain.

Financial Market

Derivatives Market – Vanilla Options – Call option

What will be CALL’s

holder profit

(K = 10 $, c = 5 $) assuming that the stock X price

is going to be:

a) S

T

= 20

$

b) S

T

= 15

$

e) S

T

= 10

$

c) S

T

= 8

$

d) S

T

= 5

$

CALL’s holder executes his right an gain: a) 10 $ b) 5 $.

Unfortunately, he has paid a 5 $ premium to a writer, hence the final

profit is going to be:

a) 5 $

b) 0 $

Profit:

CALL option is worthless, but holder has paid 5 $ premium, hence the

profit is:

c) - 5 $ d) - 5 $

Profit:

e) - 5
$

Profit:

Holder’s

payoff - premium =

Holder’s

profit

CALL option is worthless, but holder has paid 5 $ premium, hence the

profit is:

Financial Market

Derivatives Market – Vanilla Options – Call option

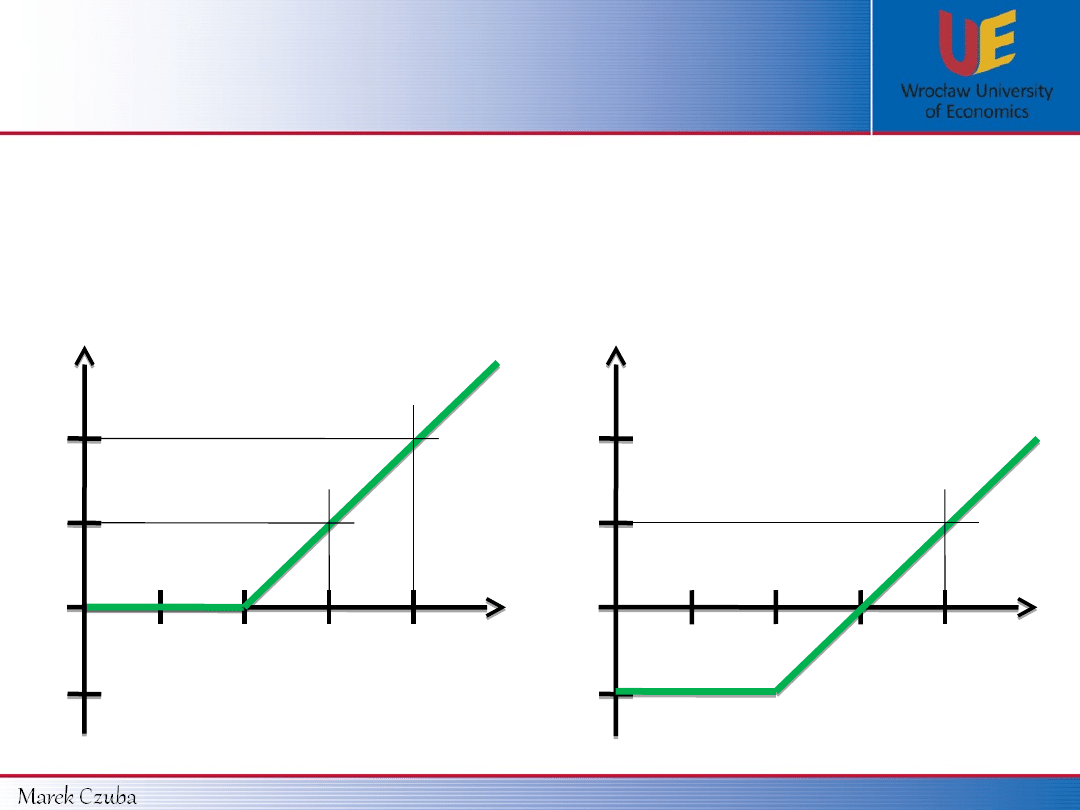
Payoff function   Profit function

for CALL’s

holder

:

10 $

0

S

T

Payoff

Payoff function (K = 10 $):

15 $

20 $

5 $

5 $

10 $

10 $

0

S

T

Profit

15 $

20 $

5 $

5 $

Profit function (K = 10 $, c = 5 $):

- 5 $

10 $

- 5 $

Financial Market

Derivatives Market – Vanilla Options – Call option

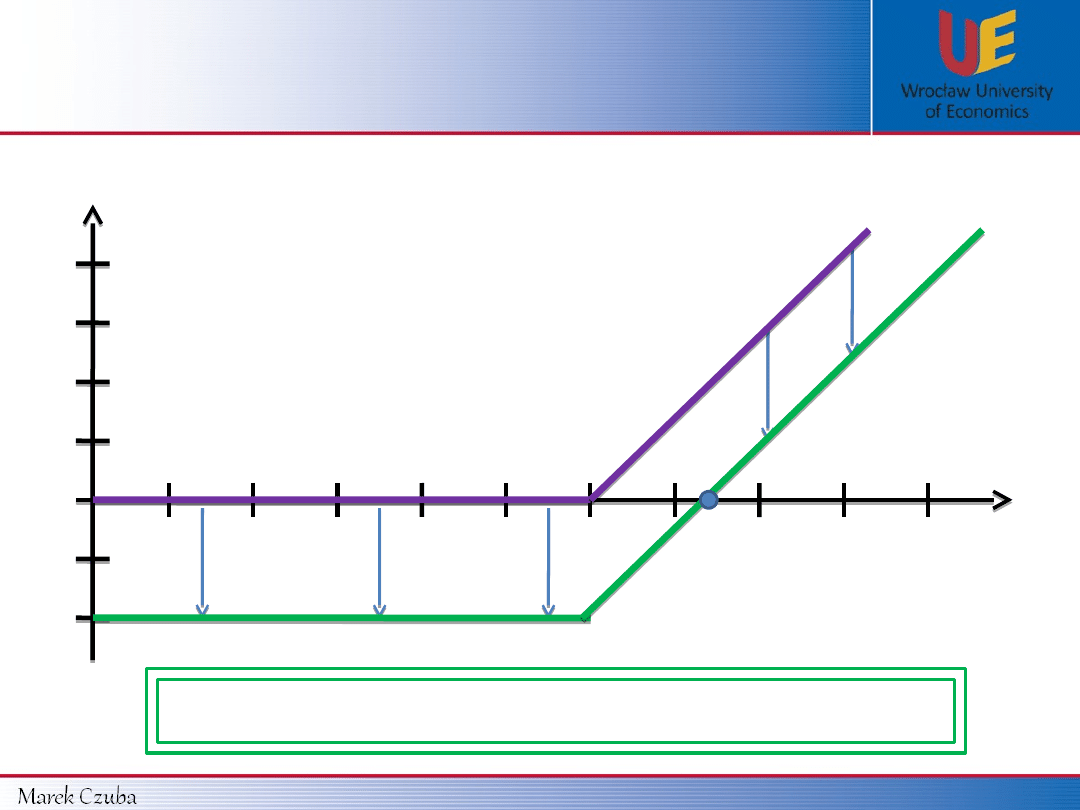
Payoff function

and

Profit function

for CALL’s

holder:

0

S

T

K

-
c

- c

- c

- c

- c

- c

K +
c

Pa

yo

ff

fu

nc

tio

n

Pr

ofi

t

fu

nc

tio

n

$

Financial Market

Derivatives Market – Vanilla Options – Call option

MAX(S

T

– K , 0)

- c

Profit function for CALL’s

holder

=

a) S

T

= 20

$

b) S

T

= 15

$

e) S

T

= 10

$

c) S

T

= 8

$

d) S

T

= 5

$

Writer will be asked to sell stock X, hence writer will make: a) - 10 $

b) - 5 $. On the other hand writer gain 5 $ premium for writing the

contract. To sum it up, writer’s profit is equal to:

a) - 5 $ b) 0 $

Profit:

CALL option is worthless. Writer’s will be left with a premium:

c) 5 $

d) 5 $

Profit:

e) 5 $

Profit:

Writer’s

payoff + premium =

Writer’s

profit

What will be CALL’s

writer profit

(K = 10 $, c = 5 $) assuming that the stock X price is going to be:

CALL option is worthless. Writer’s will be left with a premium:

Financial Market

Derivatives Market – Vanilla Options – Call option

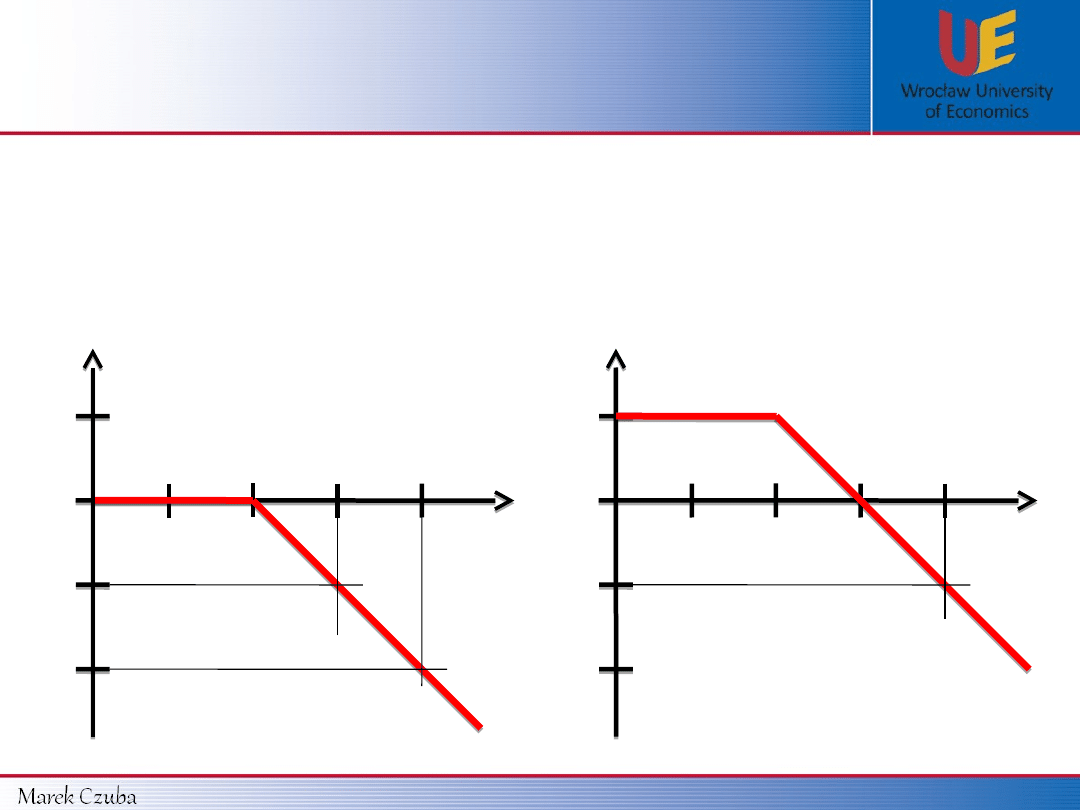
10 $

0

S

T

15 $

20 $

5 $

- 5 $

- 10 $

10 $

0

S

T

15 $

5 $

- 5 $

- 10 $

5 $

5 $

20 $

Payoff function   Profit function

for CALL’s

writer:

Payoff

Payoff function (K = 10 $):

Profit

Profit function (K = 10 $, c = 5 $):

Financial Market

Derivatives Market – Vanilla Options – Call option

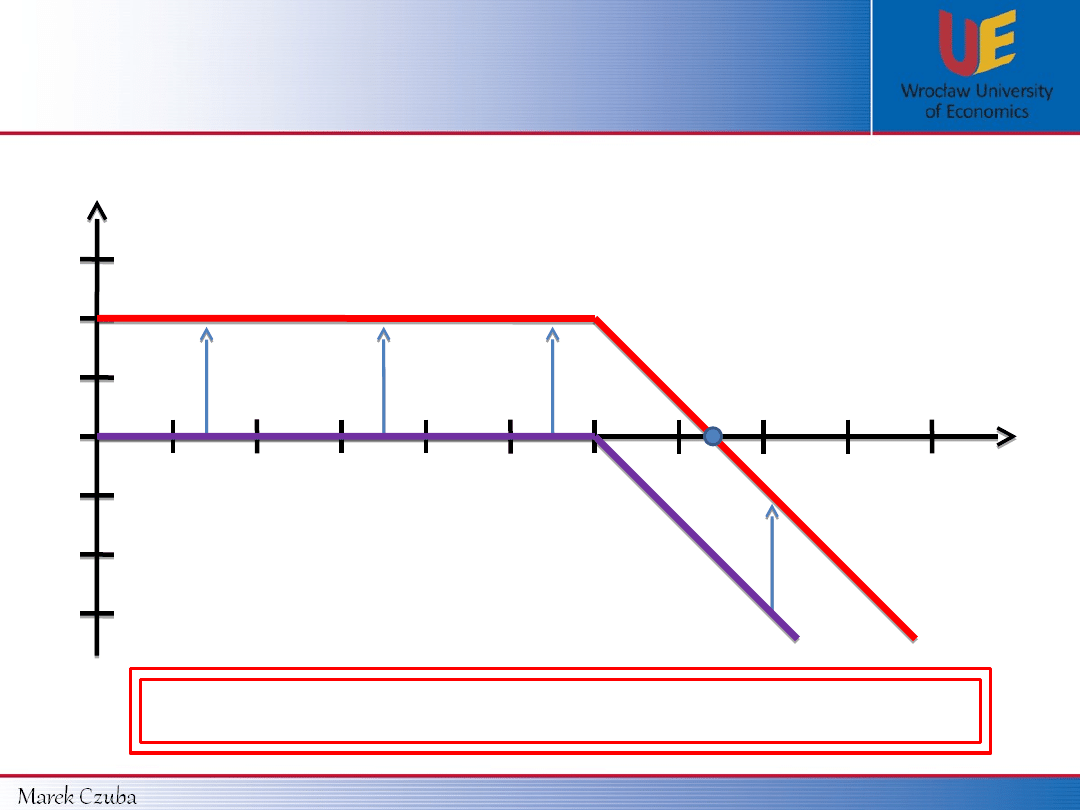
0

S

T

$

K

c

K +
c

Payoff function

Profit function

+
c

+
c

+
c

+
c

Payoff function

and

Profit function

for CALL’s

writer:

Financial Market

Derivatives Market – Vanilla Options – Call option

- MAX(S

T

– K , 0)

+ c

Profit function for CALL’s

writer

=

Payoff and Profit Functions

for CALL’s

holder

and

writer

S

T

Payoff

S

T

Payoff

S

T

Profit

S

T

Profit

HOLDER

WRITER

Financial Market

Derivatives Market – Vanilla Options – Call option

CALL Premium (c)

Option premium

Intrinsic value

Time Value

+

=

What will be an option

payoff if it would expire right

now.

Max ( S

0

– K ; 0 )

What could happen in a

future.

c – Max ( S

0

– K ; 0 )

Time value

approaches

zero

as the expiration

date nears.

Financial Market

Derivatives Market – Vanilla Options – Call option

CALL Premium (c)

CALL option premium mostly depends on:

S

0

– spot price (what is the current underlying security price).

K – Strike (execution price).

T – Time (How long this option is going to live).

When the other variables are constant then:

If

S

0

raises

then

If

S

0

falls

then

If

T raises

then

If

T falls

then

If

K raises

then

If

K falls

then

c raises too

.

c falls.

c raises too

.

c falls too

.

c raises

.

c falls too

.

Financial Market

Derivatives Market – Vanilla Options – Call option

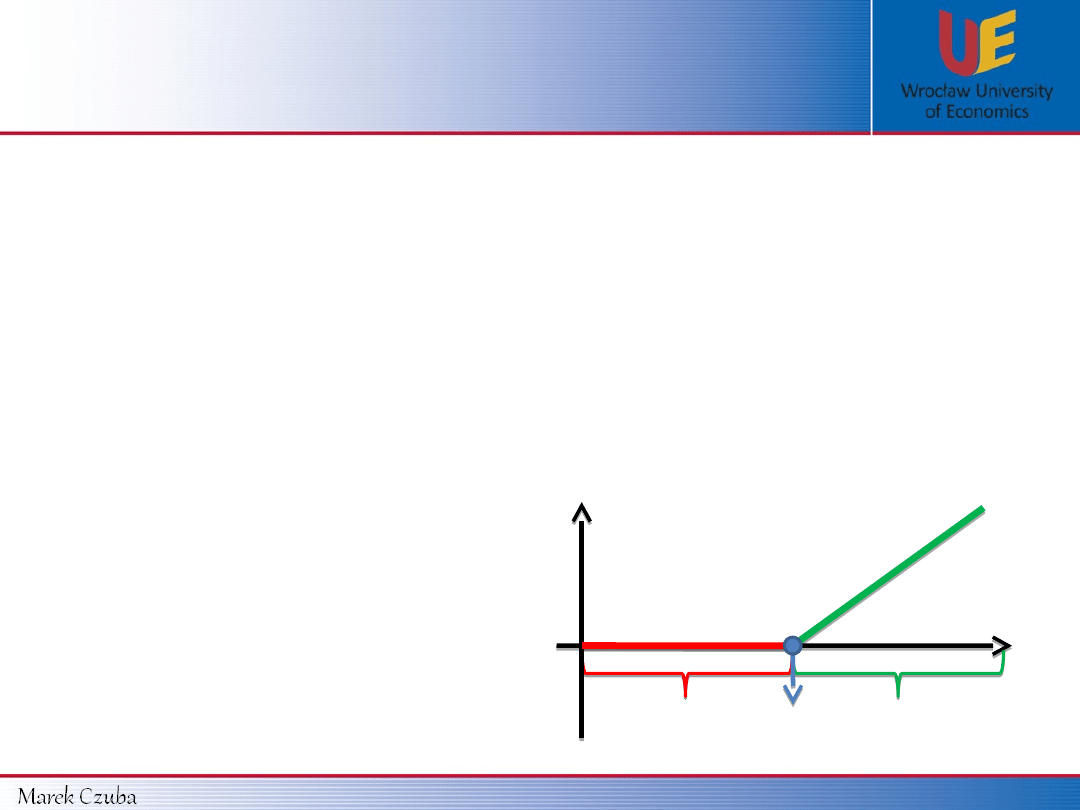
Terminology:

Based on relationship between S

0

and K we can distinguish such options:

IN the money

(ITM)

AT the money

(ATM)

OUT of the money

(OTM)

K

0

S

0

Payoff

CALL option is:

ITM

when S

0

>

K

ATM

when S

0

=

K

OTM

when S

0

<

K

ITM

ATM

OTM

Financial Market

Derivatives Market – Vanilla Options – Call option