Strength of materials – laboratory

Photoelasticity

AGH University of Science and Technology Faculty: ……………... ……………………

Kraków

Year of study ………… Group No ………

Department of Strength & Fatigue of Material & Structures

Date of exercise ………… Mark: …………

Laboratory exercises

Names: ……………………………………….

PHOTOELASTIC ANALYSES

.…………………………………..……

Task No. 1.A: Determination of the constant of the photoelastic model based on isochromatic fringe pattern observed on a beam loaded by pure bending.

1) The test stand diagram:

1

2

3

4

5

1 – source of light

2 – polarizer

3 – load frame

4 – tested specimen

5 – analyzer

DIFFUSED-LIGHT POLARISCOPE

2) The loading diagram:

2 P

P

P

σ

y

z (

)

i

y

m i

y i

h

x

z

z

g

P

P

Basic relationships:

a

a

l

σ ( ) = m ⋅ K

z y

i

(A1)

i

P

Mg( )

12 ⋅

z

Pa

T

P

(z)

σ ( ) =

⋅ y =

⋅ y

z y

i

3

i

(A2)

i

J

g

P

⋅ h

x

z

P

From eq. (1) & (2):

Pure bending

Mg

12 Pa

y

(z)

i

K =

⋅

(A3)

z

g ⋅ h 3 mi

Pa

where:

yi – coordinate of the m i order isochromatic fringe

K – constant of the photoelastic model 3) Dimensions of the specimen:

h =............... mm

g =............... mm

l =............... mm

a =............... mm

Force gage factor:

k =............... N/scale, 1/4

Strength of materials – laboratory

Photoelasticity

4) Experimental and calculation results:

Coordinate

Constant of the

Isochromatic of m

Load level

i – order

photoelastic

fringe order isochromatic

model

mi

fringe

2 P, (scale)

2 P, (N)

yi, (mm)

K, (MPa)

Kav=

Task No. 1.B: Determination of constant of the photoelastic model based on isochromatic fringe pattern observed on a compressed circular disc.

1) The loading diagram:

2) Basic relationships:

a)

Stresses in the center of disc:

2 P

σ =

6 P

;

σ = −

;

(B1)

x

y

π gD

y

π gD

P

8 P

σ −σ = σ −σ =

;

(B2)

1

2

x

y

π gD

b)

Stress-optic law:

σ −σ = m ⋅ K;

(B3)

1

2

x

c)

Model stress-optical coefficient for the circular disc (compare to eq. B2 – B3):

× g

8 P

K =

;

P

π

(B4)

gDm

where:

D, g – disk dimensions (see on the figure) m –isochromatic fringe order in the center of the disc 3) Dimensions of the disc:

D =............... mm

g =............... mm

4) Experimental and calculation results: Isochromatic

constant of the

Load level

fringe order in

photoelastic

the center of disc

model

P, (scale)

P, (N)

mi

K, (MPa)

Kav=

2/4

Strength of materials – laboratory

Photoelasticity

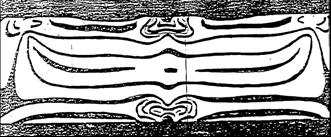
Task No. 2: Determination of the stress concentration factor ( kt) for the loaded by pure bending beam with single and double notch.

1) The loading diagram:

2 P

P

P

σ σ max

n

1 – distribution of the

1

nominal stress

z

2

2 – distribution of the

real stress

P

P

a

a

l

2) Considered specimens:

a) Model I

b) Model II

The single-notch beam:

The double-notch beam:

H

h

H

h 1

× g

× g

m max

m max

3) Basic relationships:

a) Stress concentration factor k t (definition): b) Maximum stresses at the notch tip σmax: σ max

k =

;

(2.1)

σ

= K ⋅ m ;

t

σ

max

max

(2.2)

n

where: m max – maximum isochromatic fringe order observed at the notch tip K – constant of the photoelastic model – assume K= K av (acc. to Task No. 1.A) c) Nominal stresses σn:

Model I:

Model II:

M

M

g

6 Pa

σ =

=

g

6 Pa

;

(2.3a)

σ =

=

;

(2.3b)

n

2

W

gh

n

2

W

gh

g

1

netto

g netto

3/4

Strength of materials – laboratory

Photoelasticity

4) Specimens’ dimensions:

l =................. mm

a =............... mm

H =............... mm

g =............... mm

h1 =............... mm

h =............... mm

5) Experimental and calculation results: Load level

Isochromatic

Stress concentration

Specimen:

fringe order at the

2 P, (scale)

2 P, (N)

factor - k

notch tip - m

t

max

Model I

Model II

6) Stress distributions in the loaded by pure bending beam determined based isochromatic pattern fingers:

Kav =................. MPa ( acc. to Task No. 1.A) a) The smooth beam:

y

σ, MPa

b) The single notch beam:

y

σ, MPa

c) The double notch beam:

y

σ, MPa

4/4