Równania ró·

zniczkowe zwyczajne z zasosowaniami w biologii.

Laboratorium 8. Rozwi ¾

azywanie uk÷

adów równań liniowych.

Zadanie 1.

Znaleźć rozwi ¾

azanie uk÷

adu równań ró·

zniczkowych

x0 = 2x + y

;

y0 = 3x + 4y

gdzie x = x (t) ; y = y (t) : Rozwi ¾

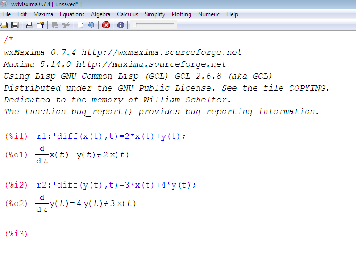
azanie w programie Maxima (Wersja 1) Wpisujemy najpierw oba równania uk÷

adu. Dla wygody podstawmy je do zmiennych: r1:’di¤(x(t),t)=2*x(t)+y(t); r2:’di¤(y(t),t)=3*x(t)+4*y(t); Mamy wi ¾

ec wpisane równania:

Zauwa·

zmy, ·

ze niewiadome funkcje musimy zapisywać podaj ¾

ac zmienn ¾

a niezale·

zn ¾

a czyli we

postaci x(t) i y(t) a nie x i y. Nast ¾

epnie, aby znaleźć rozwi ¾

azanie uk÷

adu u·

zwamy polecenia

desolve([równania],[niewiadome]) (patrz: Help programu Maxima): desolve([r1,r2],[x(t),y(t)]); 1

W efekcie otrzymujemy rozwi ¾

azanie w postaci

Zauwa·

zmy, ·

ze postać rozwi ¾

azania otrzymana za pomoc ¾

a funkcji desolve zawiera zamiast sta÷

ych dowolnych wartości szukanych funkcji w zerze.

Rozwi ¾

azanie w programie Maxima (Wersja 2) Wiemy, ·

ze macierz ¾

a fundamentaln ¾

a dla uk÷

adu o sta÷

ych wspó÷

czynnikach jest X (t) =

exp (tA) : Zgodnie ze wzorem (9.8) (patrz: Twierdzenie 9.5 w notatkach do wyk÷

adu), uwzgl ¾

ed-

niaj ¾

ac fakt, ·

ze powy·

zszy uk÷

ad równań jest uk÷

adem jednorodnym (tzn. f (t) 0) oraz fakt,

·

ze X 1 (0) = I 1 = I; otrzymujemy wzór na rozwi ¾

azanie uk÷

adu w postaci

x (t)

x (0)

= exp (tA)

:

y (t)

y (0)

W programie Maxima mo·

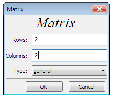
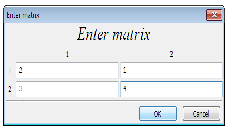
zemy wyznaczyć exp (tA) : Wprowadźmy najpierw macierz uk÷

adu

u·

zywaj ¾

ac plecena z menu programu Algebra/Enter matrix wpisuj ¾

ac odpowiednie wartości

jak poni·

zej:

2

Otrzymamy wówczas

Powy·

zej, poleceniem A:% podstawiamy wpisan ¾

a macierz uk÷

adu do zmiennej A: W pro-

gramie Maxima mo·

zemy wyznaczyć macierz exp (tA) : Wykorzystujemy pakiet diag. Czyn-imy to nast ¾

epuj ¾

aco:

1. ÷

adujemy pakiet poleceniem load("diag")$

2. u·

zywamy polecenia mat_function(exp,t*A); Otrzymamy wtedy

Jeśli oznaczymy przez x0 i y0 wartości x (0) i y (0) ; to rozwi ¾

azanie otrzymamy ze wspom-3

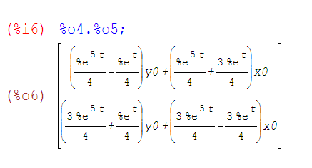
nianego na pocz ¾

atku wzoru. Mianowicie robimy to jak poni·

zej

tzn. w linii (%i5) wprowadzamy odpowiedni wektor zaś w linii (%i5) mno·

zymy macierze

zgodnie ze wzorem (: oznacza mno·

zenie macierzy).

Rozwi ¾

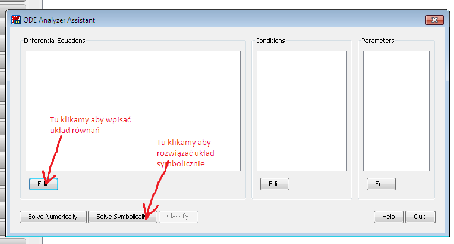
azanie w programie Maple 11 (Wersja 1) Uruchamiamy program Maple 11. Wykorzystujemy polecenie menu programu: ToolsnAssistantsnODE Analyzer...

Mianowicie

4

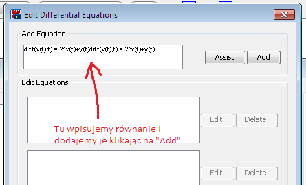
1. wpisujemy uk÷

ad równań

Po wpisaniu obu równań klikamy Done.

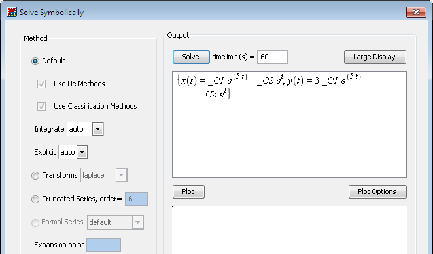
2. Po wpisaniu obu równań, rozwi ¾

azujemy uk÷

ad, klicaj ¾

ac na Solve Simbolically a nast ¾

epnie na Solve i otrzymujemy rozwi ¾

azanie uk÷

adu

Rozwi ¾

azanie w programie Maple 11 (Wersja 2) Do wyznaczania funkcji wyk÷¾

adniczej od macierzy w programie Maple s÷

u·

zy polecenie

MatrixExponential

z pakietu LinearAlgebra.

Post ¾

epujemy nast ¾

epuj ¾

aco: najpierw

5

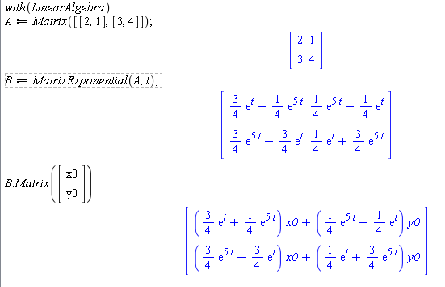
wprowadzamy macierz uk÷

adu, obliczamy macierz exp(tA) a na koniec wyznaczamy rozwi ¾

azanie:

6