XXI SYMPOZJUM – VIBRATIONS IN PHYSICAL SYSTEMS – Poznań-Kiekrz 2004
WDOWICKI Jacek, WDOWICKA Elżbieta,
Poznan University of Technology,
ul. Piotrowo 5, 60-965 Poznań, Poland
tel.: +48 61 665 24 62, E-mail: jacek.wdowicki@put.poznan.pl
SEISMIC ANALYSIS OF THE SHEAR WALL DOMINANT BUILDING
USING CONTINUOUS-DISCRETE APPROACH
1. INTRODUCTION
In tall buildings the lateral loads that arise from effects of wind and earthquakes are
often resisted by a system of coupled shear walls acting as vertical cantilevers. It is
possible to perform the analysis of shear wall structures using either the discrete method
or the continuous one. In the continuous approach, the horizontal connecting beams,
floor slabs, and vertical joints are substituted by continuous connections. In recent years
the use of continuum models in structural analysis has received considerable attention.
These models offer an attractive, low cost method for analysing large structures and they
represent the useful tool for design analysis.
For the dynamic analysis it is convenient to use a hybrid approach based on the
analysis of an equivalent continuous medium and a discrete lumped mass system
[1,4,7,8]. The coupled shear wall system is represented by either a continuous system or
a discrete system at various stages of analysis. The advantage of using these two ways of
representing of the shear wall system is that the flexibility and mass matrices required
for structural dynamic analysis are easily obtained.
The paper presents results of the seismic analysis based on the above-mentioned
method. The seismic analysis was carried out by means of the response spectrum
technique. Design spectrum for elastic analysis according to Eurocode 8, Draft No.6 [6]
was used.
2. MODEL AND THEORETICAL BACKGROUND OF ANALYSIS
In the analysed building, lateral loads that arise as a result of winds and earthquakes
are resisted by the three-dimensional system of coupled shear walls. A diaphragram
action of all floor slabs is taken into consideration as the effect of their in-plane infinite
rigidity and negligible transverse one. Owing to the height to width ratio of the shear
walls, there is a possibility to treat each wall as an open thin-walled beam, according to
Vlasov theory assumptions.
The static analysis was carried out on the basis of some variant of the continuous
connection method [9]. In this method lintel beams are treated as the equivalent shear
connection medium between shear walls, while the walls are simply regarded as vertical
cantilevers. The technique may be used for both plane and spatial structures, which are
essentially regular in form throughout the height.
Dynamic solutions have been obtained by treating the structure as a lumped parameter
system with discrete masses in the form of rigid floor slabs arbitrary located along the
height [7]. The coupled torsional-flexural vibrations have been considered because
torsional response of buildings during ambient and earthquake response is
significant. For shear wall multi-storey structure it is more natural to determine the
flexibility matrix D than stiffness matrix K. The vibration of a structure is described by the
following relation [3]:
M
D
x
&
& +
C
D
x
& + x =
F
D
(1)
where
D - flexibility matrix,
M - mass matrix,
C - damping matrix,
x - d-element vector of generalised coordinates (d - number of dynamic degrees of
freedom of the calculated structure),
F - d-element vector of generalised excitation forces, corresponding to generalised
coordinates.
Calculations were made using DAMB program (Dynamic Analysis of Multistorey
Buildings), as part of an Integrated System [10], which gives a possibility to perform linear
dynamic analysis of three-dimensional shear wall structures.
The flexibility matrix D is generated from the exact solution of the governing
differential equation for 3-D continuous model. Also mass matrix is generated exactly
according to real distribution of walls, connecting beams and floor slabs and including
flexural and torsional inertia. The seismic response of the structure is estimated using the
response spectrum technique. The involved steps are as follows: 1) determination of
natural frequencies and mode shapes, 2) evaluation of modal participation factors and
calculation of modal loading on the structure (using an appropriate design spectrum),
3) determination of response estimate taking into account the contribution from the given
number of modes for various parameters of interest (using three methods: SRSS – the
square root of the sum of the squares, CQC – the complete quadratic combination, DSC
– the double sum combination [5]).
3. RESULTS OF THE SEISMIC ANALYSIS
The results of static and free vibration analyses were presented in previous papers
[7,9]. As the numerical example of seismic analysis the shear wall dominant building,
analysed in [2] was chosen. The analysed multistorey reinforced concrete structure,
constructed by using a special tunnel form technique, is composed of vertical and
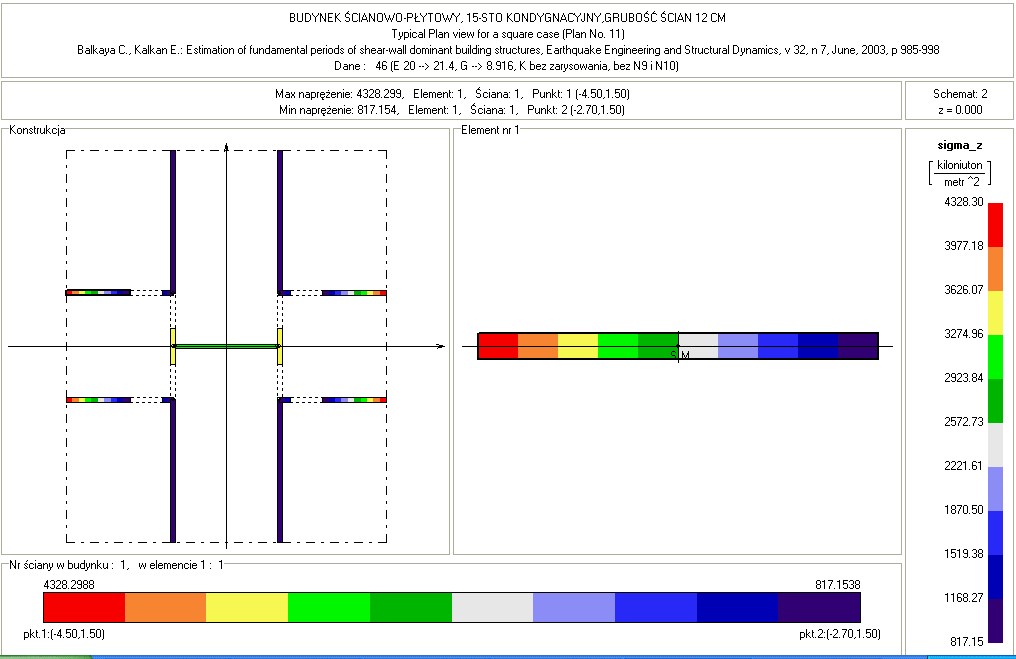
horizontal panels set right angles. The plan of the analysed structure is given in Figure 1.
The building height is 42 m, the storey height – 2.8 m and the height of connecting
beams – 0.7 m. The properties of material are taken to be E = 21.4 GPa and G =
8.92 GPa.
In the analysis the design spectrum for linear analysis according to Eurocode 8 has
been taken. The type 1 spectrum and subsoil class C ( S = 1.35, TB = 0.2, TC = 0.6,
TD = 2.0) have been considered. The value of viscous damping ratio ξ = 5% has been
assumed. The analysis has been carried out for the design ground acceleration
ag = 2.5 m/s2 . The results of the analysis based on the response spectrum technique,
obtained for the seismic wave direction parallel to X-axis, are shown in Figures 1 and 2.
4. CONCLUSIONS
In this study the seismic analysis of shear wall tall building has been carried out
using a continuous-discrete approach and the response spectrum technique. It can be
noted that in the method applied both the preparation of data is easy and the length of
computation time is short. Consequently, the software based on this method, represents
a useful tool for the design analysis.
REFERENCES
1. Aksogan O., Arslan H.M., Choo B.S., Forced vibration analysis of stiffened
coupled shear walls using continuous connection method, Engineering
Structures, 25 (2003) 499-506.
2. Balkaya C., Kalkan E., Estimation of fundamental periods of shear-wall dominant
structures, Earth. Eng. & Struct. Dyn., 32 (2002) 985-998.
3. Clough R.W., Penzien J., Dynamics of Structures, McGraw-Hill, New York 1993.
4. Li G.-Q., Choo B.S., A continuous-discrete approach to the free vibration analysis
of stiffened pierced walls on flexible foundations, Int. J. Solids and Structures., 33
(1996) 249-263.
5. Maison BF., Neuss CF., Kasai K., The comparative performance of seismic
response spectrum combination rules in building analysis, Earth. Eng. & Struct.
Dyn., 11 (1983) 623-647.
6. PrEN 1998-1:200X: Eurocode 8: Design of structures for earthquake resistance.
Part 1: General rules, seismic actions and rules for buildings. DRAFT No 6.
Version for translation (Stage 49). January 2003. CEN, Bruxelles.
7. Wdowicki J., Wdowicka E., Wrześniowski K., Free vibration of unsymmetrical
multistorey shear wall buildings, In: Proc. Third Int. Symp. on "Wall Structures".
CIB, Warsaw, Poland, 1984, vol.II: 339-346.
8. Wdowicki J., Wdowicka E., Integrated system for analysis of three-dimensional
shear wall structures, Comp. Meth. in Civil Engineering, 1 (1991) 53-60.
9. Wdowicki J., Wdowicka E., System of programs for analysis of three-dimensional
shear wall structures, The Structural Design of Tall Buildings, 2 (1993) 295- 305.
10. Wdowicki J., Wdowicka E., Błaszczyński T., Integrated system for analysis of shear
wall tall buildings, In: Proc. of the Fifth World Congress "Habitat and High- Rise:
Tradition and Innovation". Council on Tall Buildings and Urban Habitat,
Amsterdam, 1995, 1309-1324.

Figure 1. Normal stresses at the base of shear wall structure
for the seismic wave direction parallel to X-axis
Figure 2. Horizontal displacements of shear wall structure
for the seismic wave direction parallel to X-axis
Wyszukiwarka
Podobne podstrony:
SEISMIC ANALYSIS OF THE ‘SOUTH GATE’ TALL BUILDING ACCORDING TO EUROCODE 8
Analysis of spatial shear wall structures of variable cross section
An%20Analysis%20of%20the%20Data%20Obtained%20from%20Ventilat
Analysis of the Persian Gulf War
Analysis of the Holocaust
Analysis of the Infamous Watergate Scandal
Road Not Taken, The Extensive Analysis of the Poem
Analysis of the End of World War I
Night Analysis of the Novel
Preliminary Analysis of the Botany, Zoology, and Mineralogy of the Voynich Manuscript
Victory, The Analysis of the Poem
Analysis of Police Corruption In Depth Analysis of the Pro
Analysis of the First Crusade
Babi Yar Message and Writing Analysis of the Poem
Crime and Punishment Analysis of the Character Raskol
Legalization of Drugs Extensive Analysis of the?bate
Hospital Window, The Analysis of the Poem
Death of a Salesman Analysis of the Character Willy
więcej podobnych podstron