Microsoft Excel 2000
"Szukaj wyniku" i rozwiązywanie równań
Szukaj wyniku z menu Narzędzia służy do numerycznego rozwiązywania równań z jedną niewiadomą. Przydaje się w sytuacjach, gdy chcemy wymusić, by wpisana do komórki formuła osiągnęła pożądany wynik i jednocześnie dowiedzieć się, jaka wartość innej komórki, od której formuła zależy, doprowadziła do tego wyniku.
Zadanie 57.
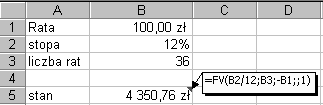
Klient wpłaca co miesiąc do banku 100 zł na 12%. Odpowiedzieć na następujące pytania:
a) Jaki będzie stan jego oszczędności po 3 latach?
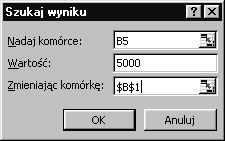
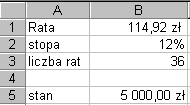
b) Ile powinna wynosić miesięczna wpłata, aby stan oszczędności po 3 latach wynosił 5000zł?
c) Jakie powinno być oprocentowanie, aby po 3 latach uzyskać 5000zł przy miesięcznej wpłacie 110 zł?
Rozwiązanie.
a) Zastosujmy funkcję finansową FV:
- 207 -
Microsoft Excel 2000
b) Ustawiając B5 jako komórkę aktywną wybieramy Narzędzia |
Szukaj wyniku... , w oknie dialogowym podajemy:
i
i otrzymamy rozwiązanie:
Komórka B5 zawiera wymuszoną wartość oszczędności, a komórka B1 wysokość raty, która do tej wartości doprowadziła.
Zadanie 58.
Rozwiązać równanie
x − 3cos2 ( ,
1 04 x) = 0 ,
wiedząc, że rozwiązanie mieści się w przedziale (2,9; 3,1).
Wartość rozwiązania 2,99837388792227.
Rozwiązanie.
Metoda I
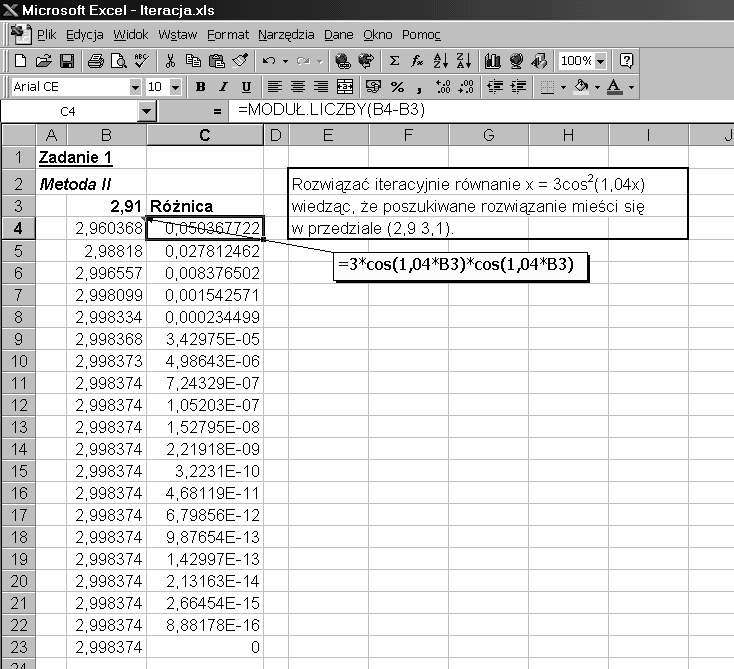
Zastosujemy narzędzie Szukaj wyniku... . Przygotowujemy arkusz jak na poniżej zamieszczonym rysunku wpisując do komórki
- 208 -
Microsoft Excel 2000
B4 formułę, a do komórki B3 wartość należącą do przedziału zawierającego rozwiązanie tzn. (2,9 3,1) np. 2,91.
Wybieramy z menu Narzędzia opcję Szukaj wyniku... i w okienku dialogowym wpisujemy odpowiednie wartości (patrz rysunek). Po kliknięciu OK otrzymujemy rozwiązania. Widać, że wartość w komórce B4 nie jest dokładnie równa 0, ale bardzo mała.
Metoda II
Dla porównania rozwiążmy to równanie inną metodą. Zastosujemy rozwiązanie polegające na wykorzystaniu przekształconego równania: x = 3cos2
04
,
1
(
x)
W komórce B3 umieszczamy wartość początkową procesu iteracyjnego. Jest to pierwszy wyraz ciągu {xn} kolejnych przybliżeń wartości rozwiązania. Przy spełnieniu warunku:
'
f ( x) < 1
- 209 -
Microsoft Excel 2000
w otoczeniu poszukiwanego rozwiązania proces iteracyjny jest zbieżny. Gwarantuje to znalezienie rozwiązania. W komórce B4
umieszczamy
formułę
obliczającą
wartość
prawej
strony
przekształconego równania dla argumentu z komórki powyżej.
Komórka C4 zawiera formułę obliczającą bezwzględną wartość różnicy kolejnych wyrazów ciągu przybliżeń. (widoczna w pasku edycji).
Wyliczenie kolejnych wyrazów ciągu przybliżeń polega na skopiowaniu formuł z komórek B4 i C4 w dół dowolną znaną metodą.
Kopiować należy tak daleko aż wartości z kolumny C staną się dostatecznie małe.
- 210 -
Microsoft Excel 2000
Zadanie 59.
Każde z poniżej zamieszczonych równań rozwiązać stosując obie wyżej omówione metody.
x − cos2 3
,
0 87 x = 0
Rozwiązanie w przedziale (0, 1)
(0,886777199701406)
1
2
10 x
x =
Rozwiązanie w przedziale (1, 2)
(1,89665100190419)
Uwaga!
Rozwiązując dwa pierwsze przykłady metodą II możemy się spotkać z rozbieżnością procesu iteracyjnego. Wynika to z niespełnienia warunku
koniecznego
zbieżności. Czasem można równanie
wyjściowe przekształcić w inny sposób do postaci x = f(x), tak aby pochodna prawej strony spełniała warunek zbieżności. Nie zawsze jest to jednak możliwe.
- 211 -
Wyszukiwarka
Podobne podstrony:
EXCEL funkcja SZUKAJ wyniku
EXCEL funkcja SZUKAJ wyniku
57-59, polski
Excel El.ster. zad 37-40
57 59
57 59
Excel Makra i VB zad 65 67(1)
57 59
57 59
57-59, polski
Szukaj wyniku
08a szukaj wyniku
07 1993 57 59
57 59 206p pol ed01 2008
więcej podobnych podstron