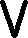
CALIC (Context-based Adaptive Lossless Image Codec)
Kryteria modelowania kontekstu dla bezstratnego kodowania obrazu w znaczeniu maksymalnej kompresji i in¿ynierskiej przydatnoœci (stosowalnoœci) s¹ nastêpuj¹ce: a) silna dekorelacja - przyjêty model obrazu pozwala ca³kowicie okreœliæ i zredukowaæ statystyczn¹
nadmiarowoœæ Ÿród³a.
b) uniwersalnoœæ - model obrazu mo¿e szybko przystosowaæ siê (adoptowaæ) do nieznanej statystyki Ÿród³a.
c) niski koszt obliczeniowy - same konteksty oraz modelowanie obrazu i predykcja oparte na tych kontekstach mog¹ byæ efektywnie obliczane (wyznaczane).
d) niskie wymagania pamiêciowe - przestrzeñ pamiêci przeznaczona do gromadzenia kontekstów i informacji zwi¹zanych z tymi kontekstami u¿ywana w modelowaniu i predykcji nie powinna byæ nadmierna.
Trzy-stopniowy schemat kodowania predykcyjnego z przeplotem.
Na ka¿dym etapie przeprowadzane jest przeplatane próbkowanie obrazu oryginalnego. Niech obraz oryginalny, wielopoziomowy ze skal¹ szaroœci, o szerokoœci W i wysokoœci H bêdzie opisany przez I i
[ , j], 0 ≤ i < W, 0 ≤ j < H .
i
j
Pierwszy etap
Drugi etap
Trzeci etap
Rys. 1. Schemat modelowania kontekstu do trzy etapowej predykcji kodowanych wartoœci w CALIC-u.
Pierwszy etap
A. tworzony jest podobraz o dwukrotnie zmniejszonej rozdzielczoœci w obu kierunkach W / 2 × H / 2 w sposób nastêpuj¹cy:
µ
I[ i
2 ,2 j] + I[ i
2 + ,
1 2 j + ]
1
[ i, j] =,
, 0 i W / 2, 0 j H / 2
2
≤ <
≤ <
B. podobraz koduje siê wykorzystuj¹c typowy kontekst dla DPCM, np.
[ i, j
]
1
[ i
,
1 j]
i
[
1, j 1] - i
[
1, j 1]
$
µ µ
µ
µ
µ
=
− +
−
+
−
−
−
+
, 0 ≤ i < W / 2, 0 ≤ j < H / 2
2
4
Wspó³czynniki predykcji zosta³y wyznaczone metod¹ regresji liniowej przy pomocy zbioru obrazów treningowych (zaokr¹glone zosta³y do potêgi dwójki ze wzglêdu na prostotê obliczeñ).
A. ten sam podobraz jest stosowany jako kontekst predykcji WH/2 pikseli obok wartoœci pikseli obrazu oryginalnego w sposób nastêpuj¹cy:
chcemy zakodowaæ wartoœci pikseli
I[ i
2 ,2 j], I[ i
2 + ,
1 2 j + ]
1 , 0 ≤ i < W / 2, 0 ≤ j < H / 2
B. liniowa predykcja - aby zakodowaæ wartoœci I[2i,2j] stosuje siê nastêpuj¹cy model liniowej predykcji: I[ i
2
,
1 2 j
]
1
I[ i
2
,
1 2 j
]
1
I[ i
2
,
1 2 j
]
1
$ x = .
0 9 [
µ i, j] +
−
+ +
−
− +
+
−
6
- 0 05
. ( I i
[2 − 2,2 j] + I i
[2 ,2 j − 2]) - 0.15( [
µ i + ,
1 j] + [
µ i, j + ]).
1
Natomiast wartoœci I[2i+1,2j+1] nie potrzeba ju¿ kodowaæ. S¹ one rekonstruowane z zale¿noœci: I[ i
2 + ,
1 2 j + ]
1 = 2 [
µ i, j]− I[ i
2 ,2 j].
Mo¿e przy tym wyst¹piæ b³¹d obciêcia reszty u³amkowej, gdy przy liczeniu œredniej diagonalnej suma dwóch wartoœci pikseli jest liczb¹ ca³kowit¹ nieparzyst¹ (mo¿na go zignorowaæ).
Trzeci etap
A. nale¿y zakodowaæ dwie pozosta³e wartoœci pikseli obrazu oryginalnego z ka¿dego elementarnego bloku czterech pikseli, a mianowicie
I[ i
2 + ,
1 2 j], I[ i
2 ,2 j + ]
1 , 0 ≤ i < W / 2, 0 ≤ j < H / 2.
Wykorzystano kontekst '360 stopni' sk³adaj¹cy siê z czterech pikseli najbli¿szego s¹siedztwa w rastrze cztero-po³¹czeniowym oraz dwóch pikseli z s¹siedztwa oœmio-po³¹czeniowego (wszystkie one s¹ ju¿
wczeœniej kodowane oraz dekodowane, a wiêc dostêpne w procesie rekonstrukcji).
B. zastosowano nastêpuj¹cy model predykcji:
3
I[ i
,
1 j
]
1
I[ i
,
1 j
]
1
$ x = ( I[ i − ,
1 j] + I[ i, j − ]
1 + I[ i + ,
1 j] + I[ i, j + ])
1 −
−
− +
+
−
8
4
Modelowanie i kwantyzacja kontekstu.
Dot¹d dla modelowania kontekstów predykcji poszczególnych pikseli wykorzystywano wartoœci odpowiednio K = 4, 9, 6 (1,2 i 3 etap) s¹siednich pikseli Aby przy entropijnym kodowaniu uzyskaæ minimaln¹
d³ugoœæ kodu wyjœciowego dla zbioru wartoœci e = x − x$ (gdzie $ x wyznaczono dla ka¿dej wartoœci x w trójetapowej predykcji) potrzeba maksymalizowaæ prawdopodobieñstwo warunkowe p( e / x ,..., x ).
1
K
U¿ywaj¹c standardowych metod np. kodowania arytmetycznego z za³o¿onym modelem Markowa n - tego rzêdu potrzeba by okreœliæ w sposób istotny statystycznie model o 2 ZK stanach ( Z- liczba poziomów szaroœci), co jest niebagatelnym problemem! (tzw. problem rozrzedzenia kontekstu). Zastosowano wiêc nastêpuj¹cy model kwantyzacji kontekstu w celu prostszego okreœlenia wartoœci prawdopodobieñstw warunkowych oraz korekcji przewidywanej wartoœci w pêtli sprzê¿enia zwrotnego. Tak wiêc:
A. aby u³atwiæ modelowanie kontekstu b³êdów DPCM kwantyzuje siê kontekst x , x ,..., x zwi¹zany z 1
2
K
przewidywan¹ wartoœci¹ $ x do liczby binarnej t = t ... t sk³adaj¹cej siê z K bitów tak, ¿e: K
1
0
x
if
≥ x$
t
k
=
, 1 ≤ k ≤ K.
k
1 x
if
< x
$
k
Liczba t reprezentuje wy¿szego rzêdu przestrzenn¹ strukturê modeluj¹cego kontekstu, czyli cechê obrazu, która mo¿e wskazywaæ na zachowanie siê b³êdu predykcji DPCM (korelacja). Mo¿na w ten sposób uwzglêdniæ krawêdzie, rogi, tekstury, które nie mog³y byæ uchwycone przez DPCM.
B. obliczana jest tak¿e wartoœæ dyskryminatora mocy b³êdu, który charakteryzuje zmiennoœæ wartoœci kontekstu (jego g³adkoœæ), w nastêpuj¹cy sposób:
K
∆ =
|
$|.
k −
∑ w x x
k
k =1
Na jej podstawie mo¿na estymowaæ prawdopodobieñstwo warunkowe b³êdu predykcji jako p(e/ ) zamiast p( e / x ,..., x ). Aby zlikwidowaæ problem 'rozrzedzenia kontekstu' przy estymacji p(e/ ) dokonywana jest 1
K
kwantyzacja wartoœci na L poziomów (w praktyce najczêœciej L= 8). £¹cz¹c teraz, jako iloczyn kartezjañski L
K
× 2 , kwantowany do L poziomów dyskryminator oraz 2 K kwantowanych wzorców tekstury kontekstu t otrzymujemy ostatecznie kwantyzacjê 2 ZK stanów Ÿród³a Markowa w znacznie zredukowan¹
k
liczbê L K
2 stanów. Te stany nazywane s¹ kwantowanym kontekstem i oznaczone s¹ nastêpuj¹co: C d t 0 ≤ d < L 0 ≤ t
K
( , ),
,
< 2 .
Pozostaje oczywiœcie problem jak dobraæ wartoœci wspó³czynników w . Wartoœæ jest ustalana jako k
œredniokwadratowa estymata | e|. Stosuj¹c standardow¹ metodê regresji liniowej okreœla siê wiêc wartoœci K
wspó³czynników w . Tak wiêc maj¹c przyk³adowy predyktor DPCM $ x =
a x (w jednym z trzech
k
∑ k k
k =1
etapów predykcji), jest wyznaczany treningowy zbiór S wartoœci | |
e =| x − $|
x oraz | x − $ x|,1 ≤ k ≤ K .
k
Nastêpnie wartoœci w , 1 ≤ k ≤ K s¹ obliczane metod¹ regresji liniowej tak, aby zminimalizowaæ wartoœæ: k
K
{| |
e − } =
| x
∑ ∆ ∑ − $ x|− w | x − $| x
∑ k k
S
S
k =1
na treningowym zbiorze danych.
Adaptacyjne, oparte na kontekœcie modelowanie b³êdu (wraz z drug¹ faz¹ kwantyzacji) Jednak L K
2 stanów kontekstów modeluj¹cych to jednak dalej za du¿o do dobrej estymacji prawdopodobieñstw warunkowych, w tym przypadku p(e/C(d,t)). Wobec tego nastêpuje: A. estymowanie warunkowej wartoœci oczekiwanej E{e/C(d,t)} poprzez wyznaczenie odpowiedniej œredniej próbek e( d, t) dla ró¿nych kwantowanych kontekstów. Intuicyjnie znacznie mniej próbek potrzeba do dobrej estymacji warunkowej wartoœci oczekiwanej ni¿ prawdopodobieñstwa ( O( n− .05)
O( n− .04
versus
)). Poniewa¿ œrednia warunkowa e( d, t) lepiej estymuje b³¹d predykcji DPCM w kwantowanym kontekœcie C(d,t), mo¿na skompensowaæ b³¹d DPCM poprzez modyfikacjê predykcji x z $ x na predykcjê x z & x = $ x + e( d, t) . & x jest nowym, adaptacyjnym nieliniowym opartym na kontekœcie predyktorem (mechanizm sprzê¿enia zwrotnego b³êdu predykcji z opóŸnieniem jednego kroku). Wykorzystuj¹c nowy predyktor mamy teraz nowy b³¹d predykcji: ε = x − x& dla entropijnego kodowania b³êdu. Rozk³ad wartoœci b³êdu predykcji zachowuje w tym przypadku postaæ rozk³adu Laplace'a, ale jest wyraŸnie wyostrzony.
B. optymalizacja kwantyzatora Q wartoœci Kryterium kwantyzacji jest minimalizacja warunkowej entropii wartoœci b³êdów zale¿nej od p( /Q( )). Ze zbioru obrazów treningowych obliczamy zbiór wartoœci par ( ) i u¿ywamy standardowej dynamicznej techniki wyboru wartoœci 0 = q < q < ⋅⋅⋅ < q q
L− <
L = ∞
0
1
1
dziel¹ce przedzia³ wartoœci na L podprzedzia³ów:
S = { ε| q ≤ ∆ < q } , takich ¿e wra¿enie: d
d
d +1
−
( ε)log ( ε| ε ∈
∑ p
p
S )
d
ε
osi¹ga minimum.
Dwa procesy poszukiwania optymalnego schematu kwantyzacji (szukanie wspó³czynników i podzia³
przedzia³u wartoœci na L podprzedzia³ów) mog¹ byæ przeprowadzane równie¿ w sposób ³¹czny (kwantyzacja ³¹czna).
C. entropijne kodowanie wartoœci - adaptacyjne entropijne kodowanie (najlepiej arytmetyczne) z u¿yciem tylko L prawdopodobieñstw warunkowych p( /Q( ) =d), 0 ≤ d < L dla poszczególnych wartoœci .
Przerzucanie znaku b³êdu predykcji
Znaki warunkowych œrednich próbek ε ( d, t) mog¹ byæ u¿yte do wyostrzenia prawdopodobieñstw warunkowych p( /Q( ) =d), a wiêc redukcji warunkowej entropii. Dla dwóch ró¿nych kontekstów C( d , t ) i 1
C( d , t ), wartoœci warunkowych œrednich próbek ε ( d, t ) i ε ( d, t ) mog¹ mieæ przeciwne znaki i 2
1
2
odpowiednio ró¿ne wartoœci p( ε| C( d, t )) i p( ε| C( d, t )) . Dla ustalonej wartoœci 0 ≤ d < L mo¿na 1
2
rozdzieliæ prawdopodobieñstwo p( /Q( ) =d) na dwa: p ( ε| d) p( ε| d, ε ( d, t
+
=
) ≥ )
0 , p ( ε| d) p( ε| d, ε ( d, t
−
=
) < )
0 .
Oczywistym jest, ¿e oba prawdopodobieñstwa warunkowe p i p daj¹ ni¿sz¹ entropiê ni¿
+
−
p( /Q( ) =d) (bardziej wyró¿niona jest statystyka b³êdu). Wydaje siê jednak ¿e wówczas podwajaj¹ siê: zu¿ycie pamiêci oraz rozmycie kontekstów.
Mo¿na zaobserwowaæ, ¿e p ( ε| Q(∆) d
+
= ) oraz p ( ε| Q(∆) d
−
= ) s¹ w przybli¿eniu swoim
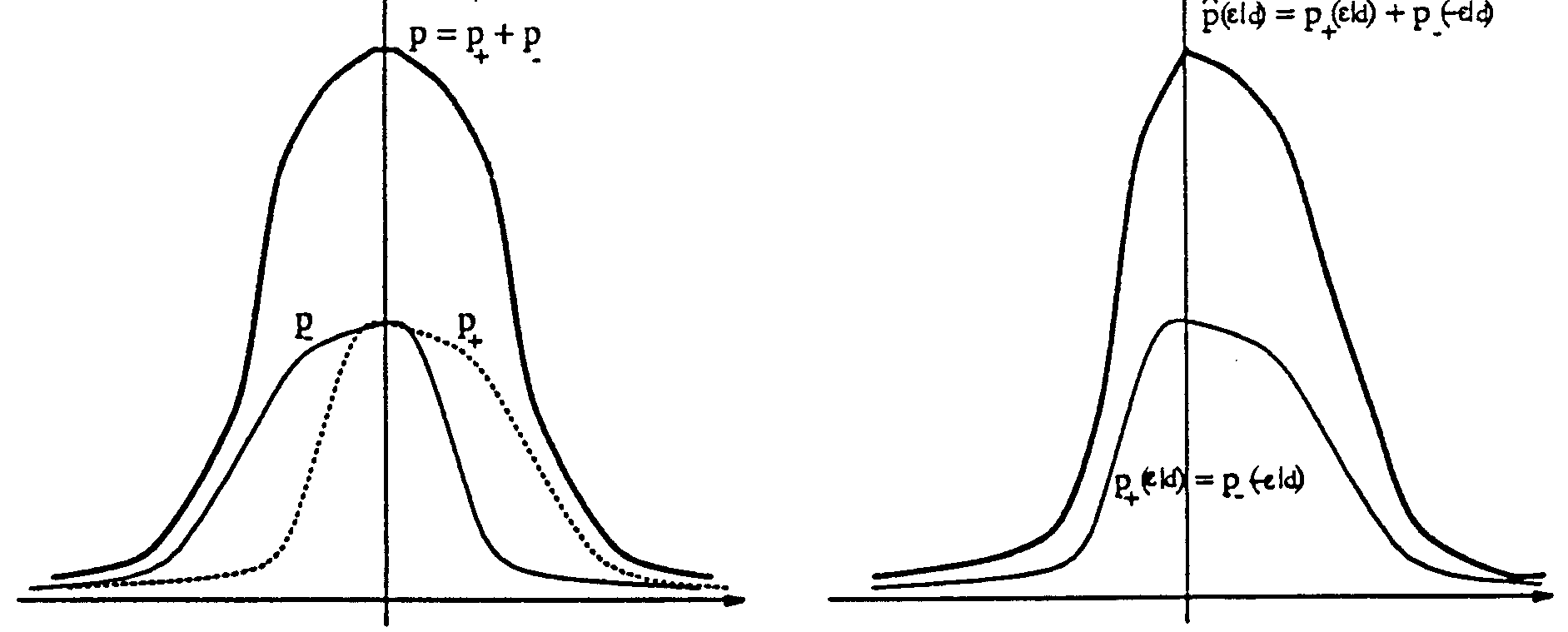
lustrzanym odbiciem wzglêdem wartoœci oczekiwanej (równej zero) rozk³adu p = p
. Mo¿na wiêc
+ + p−
przerzuciæ p symetrycznie wzglêdem osi zerowej (
ε
) i na³o¿yæ na p otrzymuj¹c obci¹¿any
−
p ( | d
− −
)
+
estymator prawdopodobieñstwa $(
p ε| Q(∆) = d) o mniejszej wariancji w stosunku do p( /Q( ) =d) - rys. 2.
Zastosowanie tego estymatora pozwala zmniejszyæ œredni¹ bitow¹ kodu bez dodatkowej pamiêci oraz bez rozrzedzenia kontekstu.
Dzia³anie: przed kodowaniem ε = x − x& , koder sprawdza czy ε ( d, t) < 0 na podstawie kontekstu C(d,t).
Jeœli tak - jest kodowany, a w pozosta³ych przypadkach . Poniewa¿ dekoder tak¿e zna C(d,t) i ε ( d, t) mo¿e jeœli to konieczne odwróciæ znak, aby zrekonstruowaæ wartoœæ ε.
Rys. 2. Wyostrzanie prawdopodobieñstwa warunkowego p = p poprzez przerzucanie p .
+ + p−
−
Najwa¿niejsze zalety metody kompresji CALIC
Z³agodzenie problemu rozrzedzenia kontekstu poprzez:
• rozró¿nienie kontekstu C(d,t) dla modelowania b³êdu oraz kontekstu Q( ) dla warunkowego kodowania entropijnego b³êdu predykcji;
• estymatê pojedynczego parametru wartoœci oczekiwanej zamiast szeregu prawdopodobieñstw warunkowych dla danego kontekstu.
Pozwoli³o to uzyskaæ du¿¹ liczbê kontekstów przy modelowaniu b³êdu, aby uchwyciæ bardziej z³o¿one struktury b³êdu (z³o¿one korelacje) w celu zwiêkszenie efektywnoœci kodowania.
Opis algorytmu
Algorytm sk³ada siê z trzech g³ównych sk³adników:
• adaptacyjna predykcja,
• modelowanie kontekstu,
• kodowanie z entropi¹ warunkow¹,
przy czym modelowanie kontekstu wp³ywa zarówno na predykcjê jak i entropijne kodowanie.
Algorytm:
Dla ka¿dego z trzech etapów:
INICJALIZACJA: N(d,t)= 1, S(d,t)= 0, 0 ≤ d < L, 0 ≤ t < 2 K .
PARAMETRY: wyznaczone wczeœniej optymalne wartoœci a , w ,1 ≤ k ≤ K.
k
k
Dla ka¿dego piksela x z danego etapu
^
K
0. x =
a x
x , x ,..., x
∑ dla kontekstu predykcji
;
k k
1
2
K
k =1
K
^
1. ∆ = ∑ w ( x - x);
k
k
k =1
2. d=Q( );
3. wyznacz wzorzec tekstury t = t ... t : K
1
^
IF ( x < x) t = 0 ELSE t = ,
1 1 ≤ k ≤ K;
k
k
k
_
4. e = S( d , t) / N ( d , t);
.
^
_
5. x = x+ e;.
6. ε = x − x;
7. S(d,t)=S(d,t)+ ; N(d,t)=N(d,t)+1;
8. IF N ( d , t) ≥ 128
S( d , t) = S( d , t) / ; 2 N ( d , t) = N ( d, t) / ; 2
9. IF S(d,t)<0 koduj (- ,d) ELSE koduj ( ,d); END;
END.