Matemat

yk

a

dyskretna

materiaªy

¢wiczenio

w

e

Studia

dzienne

PJWSTK

SPRA

WDZIAN

I

I

Imi¦

i

nazwisk

o:

Nr

indeksu:

Nr

grup

y:

Uw

aga!

Spra

wdzian

jest

testem

wielokrotnego

wyb

oru,

gdzie

wszystkie

mo»liw

e

k

om

binacje

o

dp

o

wiedzi

s¡

dopuszczalne

(tj.

zaró

wno

wszystkie

o

dp

o

wiedzi

p

opra

wne,

cz¦±¢

o

dp

o

wiedzi

p

opra

wna

jak

i

brak

o

dp

o

wiedzi

p

opra

wn

yc

h).

P

opra

wne

o

dp

o

wiedzi

nale»y

zaznaczy¢,

z

lew

ej

stron

y

k

artki,

sym

b

olem

+.

Natomiast

sym

b

ol

-

jak

i

brak

sym

b

olu

przy

o

dp

o

wiedzi

oznacza

o

dp

o

wied¹

niep

opra

wn¡.

Pytanie

jest

uznane

za

p

opra

wnie

rozwi¡zane

(tj.

+1pkt)

wtedy

i

t

ylk

o

wtedy

gdy

wszystkie

jego

o

dp

o

wiedzi

zaznaczone

s¡

p

opra

wnie.

›yczym

y

p

o

w

o

dzenia

...

1.

Która

z

p

oni»szyc

h

relacji

jest

funk

cj¡:

r ⊆ N × N r = {(x, y) : min (x, y) = 7}

(a)

[]

,

,

r ⊆ R × R r = (x, y) : y = cos x2

(b)

[+]

,

,

r ⊆ {a, b, c} × {1, 2, 3, 4} r = {(a, 1) , (b, 2) , (c, 3) , (c, 4)}

(c)

[]

,

?

f : X → Y

2.

Niec

h

b

¦dzie

funk

cj¡,

je»eli:

X = R f (x) = x2

Y =

(f ) = R

(a)

[]

i

,

to

Im

,

X = R f (x) = x2

Y ⊇

(f )

(b)

[+]

i

,

to

Im

,

X = R f (x) = x2

Y ∩

(f ) = R+ ∪ {0}

(c)

[+]

i

,

to

Im

.

f : R → R

3.

Niec

h

b

¦dzie

funk

cj¡,

je»eli:

f (x) = |x| + π

f

(a)

[]

2 , to funkcja

nie

jest

suriek

cj¡,

ale

jest

iniek

cj¡,

f (x) = sin (x) − π

f

(b)

[]

2 , to funkcja

jest

suriek

cj¡,

ale

nie

jest

iniek

cj¡,

f (x) = 1

x 6= 0

f (0) = 0

f

(c)

[+]

,

dla

oraz

,

to

funk

cja

jest

bijek

cj¡.

x

f : R \ {0} → R

f (x) = 1

4.

Rozw

a»m

y

funk

cj¦

,

gdzie

,

wtedy:

x

A = [−1, 1]

f (A) = (0, ∞)

(a)

[]

dla

zac

ho

dzi

,

B = (1, 2)

f

−1 (B) = −1, − 1 ∪ 1 , 1

(b)

[+]

dla

zac

ho

dzi

2

2

,

C = 1 , 1

f (C) ∩ f −1 (C) = ∅

(c)

[]

dla

2

zac

ho

dzi

.

f : R → R

5.

Niec

h

b

¦dzie

funk

cj¡,

je»eli:

f (x) = ||x| − 2|

f

1

−1 (x) =

|x| − 1

(a)

[]

,

to

2

,

√

f (x) = x5 + 5

f −1 (x) =

x − 5

(b)

[]

,

to

,

f (x) = f −1 (x)

f (x) = x

(c)

[+]

,

to

.

f : R → R g : R → R h : R → R

6.

Niec

h

,

,

b

¦d¡

funk

cjami,

je»eli:

f (x) = x2 g (x) = 2x h (x) = sin x (g ◦ f ◦ h) (x) = sin 2x2

(a)

[]

,

,

,

to

,

f (x) = sin x g (x) = 2x h (x) = x2

(g ◦ f ◦ h) (x) = (2 sin (x))2

(b)

[]

,

,

,

to

,

((f ◦ g) ◦ h) (x) = (f ◦ (g ◦ h)) (x) f (x) = g (x) = h (x)

(c)

[]

,

to

.

1

P

a

w

eª

Remb

elski

Matemat

yk

a

dyskretna

materiaªy

¢wiczenio

w

e

Studia

dzienne

PJWSTK

7.

Który

z

p

oni»szyc

h

ci¡

gó

w

funk

cji

jest

up

orz¡dk

o

w

an

y

rosn¡co

wzgl¦dem

rz¦dó

w

funk

cji

skªado-

wyc

h:

√

√

lg n2,

n, n n, lg n!

(a)

[]

,

√

n lg n, n n, 2n, 9 n2

(b)

[+]

,

2lg n, n2, n!, (n − 1)n−2

(c)

[+]

?

√

f (n) = n n

8.

Które

z

p

oni»szyc

h

oszaco

w

a«

jest

p

opra

wne

dla

funk

cji

:

f (n) = Ω (n lg n)

(a)

[+]

,

f (n) = O (n lg n)

(b)

[]

,

f (n) = Θ n2 − c

0 < c < 1

(c)

[]

,

gdzie

jest

p

ewn¡

staª¡?

r1

r2

9.

Niec

h

b

¦dzie

relacj¡

zwrotn¡

i

symetryczn¡

oraz

b

¦dzie

relacj¡

symetryczn¡

i

przec

ho

dni¡,

wtedy:

r1 ∩ r2

(a)

[+]

jest

relacj¡

zwrotn¡,

symetryczn¡

i

przec

ho

dni¡,

r1 ∪ r2

(b)

[]

jest

relacj¡

zwrotn¡,

symetryczn¡

i

przec

ho

dni¡,

r1 ⊕ r2

(c)

[]

jest

relacj¡

zwrotn¡,

symetryczn¡

i

przec

ho

dni¡.

r = {(a, b) ∈ N × N : a + b = 0

2}

10.

Rozw

a»m

y

relacj¦

mo

d

,

wtedy:

r

(a)

[]

relacja

jest

zwrotna,

przec

ho

dnia

i

sp

ó

jna,

r

(b)

[+]

relacja

nie

jest

przeciwsymetryczna

i

an

t

ysymetryczna,

r

N

(c)

[+]

relacja

jest

relacj¡

ró

wno

w

a»no±ci

w

zbiorze

.

r

N

5

11.

Zaªó»m

y

,

»e

graf

p

ewnej

relacji

ró

wno

w

a»no±ci

w

zbiorze

skªada

si¦

z

-ciu

rozª¡czn

yc

h

p

o

dgra-

fó

w,

wtedy:

r

N

(a)

[]

liczba

klas

abstrak

cji,

na

jakie

relacja

dzieli

zb

ór

jest

nieokre±lona,

r

N

5

(b)

[+]

relacja

dzieli

zbiór

na

co

na

jwy»ej

klas

abstrak

cji,

r

N

5

(c)

[]

relacja

dzieli

zbiór

na

klas

abstrak

cji,

z

któryc

h

k

a»da

za

wiera

sk

o«czon¡

liczb

¦

elemen

tó

w.

r ⊆ N × N r = {(x, y) : x · y ≥ 0}

12.

Niec

h

,

,

wtedy:

r−1

(a)

[]

jest

relacj¡

symetryczn¡,

przeciwsymetryczn¡

oraz

an

t

ysymetryczn¡,

r−1 ◦ r−1

(b)

[+]

jest

relacj¡

zwrotn¡

i

sp

ó

jn¡,

r−1 ◦ r ◦ r−1 = ∅

(c)

[]

.

r ⊆ (N × N)2

(x1, y1) r (x2, y2)

x1 < x2

(x1 = x2 y1 ≤ y2)

13.

Niec

h

oraz

wtt

w,

gdy

lub

i

,

wtedy:

r

N × N

(a)

[+]

relacja

jest

relacj¡

p

orz¡dku

cz¦±cio

w

ego

w

zbiorze

,

r

N × N

(b)

[+]

relacja

jest

relacj¡

p

orz¡dku

linio

w

ego

w

zbiorze

,

r

N × N

(c)

[+]

relacja

jest

relacj¡

p

orz¡dku

dobrego

w

zbiorze

.

2

P

a

w

eª

Remb

elski

Matemat

yk

a

dyskretna

materiaªy

¢wiczenio

w

e

Studia

dzienne

PJWSTK

X = {a, c, d, f, g, k, s, x, z}

r

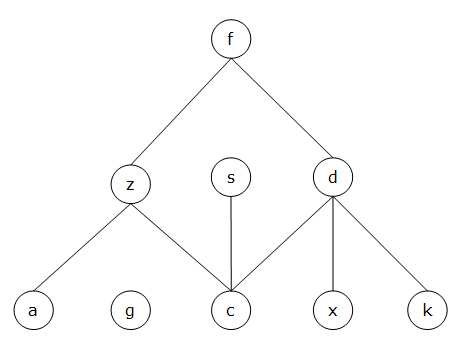
14.

Rozw

a»m

y

zbiór

up

orz¡dk

o

w

an

y

relacj¡

zgo

dnie

z

p

oni»szym

diagra-

mem

Hassego,

wtedy:

(X, r)

a c x

(a)

[+]

elemen

tem

minimaln

ym

zbioru

jest

,

,

,

(X, r)

g f

(b)

[]

elemen

tem

maksymaln

ym

zbioru

jest

,

i

s¡

to

wszystkie

elemen

t

y

maksymalne,

(X, r)

c

(X, r)

(c)

[]

elemen

tem

na

jmniejszym

zbioru

jest

lub

elemen

tem

na

jwi¦kszym

zbioru

jest

f .

(X, r)

15.

Rozw

a»m

y

zbiór

zdenio

w

an

y

w

zadaniu

14-st

ym,

wtedy:

{z, s, d}

r

c

(a)

[+]

ograniczeniem

doln

ym

zbioru

wzgl¦dem

relacji

jest

elemen

t

,

{c, x, k}

r

d

f

(b)

[]

ograniczeniem

górn

ym

zbioru

wzgl¦dem

relacji

jest

elemen

t

alb

o

,

sup {s, d} = f

inf {s, d} = c

(c)

[+]

lub

.

16.

W

jakiej

sali

o

db

yw

a

j¡

si¦

za

j¦cia

¢wiczenio

w

e

z

matemat

yki

dyskretnej:

(a)

je»eli

nie

w

C101,

to

w

D301,

(b)

gimnast

ycznej,

(c)

nie

mam

takic

h

za

j¦¢.

3

P

a

w

eª

Remb

elski