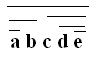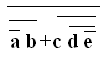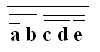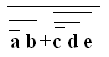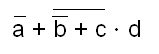
Zadanie 1.

A) Przekształć wyrażenie logiczne do postaci iloczynu sum i sumy iloczynów: B) Wykorzystując prawa de Morgana przekształć wyrażenie logiczne tak by występowały jedynie operacje negacji i mnożenia

Zadanie 2

A) Przedstaw postać binarną – zapis uzupełnienia do 2 następujące liczby dziesiętne:

-2.47, -233, 0.31 (z dokładnością do 8 cyfr binarnych)

B) Dodaj i odejmij w zapisie uzupełnienia do 2 następujące argumenty:

-197 i +205

C) Pomnóż następujące dwa ułamki jednym z wariantów metody Bootha

29

−

27

i

32

32

Zadanie 3.

A) Przyjmując, że ^ oznacza operator potęgowania, a w ONP Arg1 Op Arg2 oznaczamy Arg1 Arg2 Op Zamień z ONP na postać algebraiczną następujący zapis

a 2 ^ b 2 ^ + c d – ½ ^ / g h + 5 ^ *

B) Zamień na zapis ONP następujące wyrażenie algebraiczne

3 ( a + b) * ( c − d)

5

g * ( h − )

4

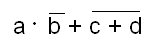
Zadanie 1.

A) Przekształć wyrażenie logiczne do postaci iloczynu sum i sumy iloczynów: B) Wykorzystując prawa de Morgana przekształć wyrażenie logiczne tak by występowały jedynie operacje negacji i mnożenia

Zadanie 2

A) Przedstaw postać binarną – zapis uzupełnienia do 2 następujące liczby dziesiętne:

-2.39, -234, 0.23 (z dokładnością do 8 cyfr binarnych)

B) Dodaj i odejmij w zapisie uzupełnienia do 2 następujące argumenty:

-197 i +203

C) Pomnóż następujące dwa ułamki jednym z wariantów metody Bootha

29

27

i −

32

32

Zadanie 3.

A) Przyjmując, że ^ oznacza operator potęgowania, a w ONP Arg1 Op Arg2 oznaczamy Arg1 Arg2 Op Zamień z ONP na postać algebraiczną następujący zapis

a 2 ^ b 2 ^ + c d – ½ ^ / g h + 5 ^ *

B) Zamień na zapis ONP następujące wyrażenie algebraiczne

3 ( a + b) * ( c − d)

5

g * ( h − )

4

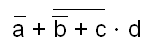
Zadanie 1.

A) Przekształć wyrażenie logiczne do postaci iloczynu sum i sumy iloczynów: B) Wykorzystując prawa de Morgana przekształć wyrażenie logiczne tak by występowały jedynie operacje negacji i mnożenia

Zadanie 2

A) Przedstaw postać binarną – zapis uzupełnienia do 2 następujące liczby dziesiętne:

-2.35, -273, 0.39 (z dokładnością do 8 cyfr binarnych)

B) Dodaj i odejmij w zapisie uzupełnienia do 2 następujące argumenty:

-199 i +203

C) Pomnóż następujące dwa ułamki jednym z wariantów metody Bootha

29

−

27

i

32

32

Zadanie 3.

A) Przyjmując, że ^ oznacza operator potęgowania, a w ONP Arg1 Op Arg2 oznaczamy Arg1 Arg2 Op Zamień z ONP na postać algebraiczną następujący zapis

a 2 ^ b 2 ^ + c d – ½ ^ / g h + 5 ^ *

B) Zamień na zapis ONP następujące wyrażenie algebraiczne

3 ( a + b) * ( c − d)

5

g * ( h − )

4

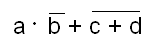
Zadanie 1.

A) Przekształć wyrażenie logiczne do postaci iloczynu sum i sumy iloczynów: B) Wykorzystując prawa de Morgana przekształć wyrażenie logiczne tak by występowały jedynie operacje negacji i mnożenia

Zadanie 2

A) Przedstaw postać binarną – zapis uzupełnienia do 2 następujące liczby dziesiętne:

-2.47, -347, 0.49 (z dokładnością do 8 cyfr binarnych)

B) Dodaj i odejmij w zapisie uzupełnienia do 2 następujące argumenty:

-199 i +207

C) Pomnóż następujące dwa ułamki jednym z wariantów metody Bootha

29

−

27

i

32

32

Zadanie 3.

A)

Przyjmując, że ^ oznacza operator potęgowania, a w ONP Arg1 Op Arg2

oznaczamy Arg1 Arg2 Op Zamień z ONP na postać algebraiczną następujący zapis a 2 ^ b 2 ^ + c d – ½ ^ / g h + 5 ^ *

B)

Zamień na zapis ONP następujące wyrażenie algebraiczne

3 ( a + b) * ( c − d)

5

g * ( h − )

4

1 Przekształcić funkcję logiczną F do postaci sumy

iloczynów: F = a + b * c + d

2 Przekształcić funkcję logiczną F, aby zawierała jedynie

operatory iloczynu i negacji. Wykorzystać do tego prawa

d’Morgana F ( a, b, c, d ) = ( a * b + c) * d + b * d

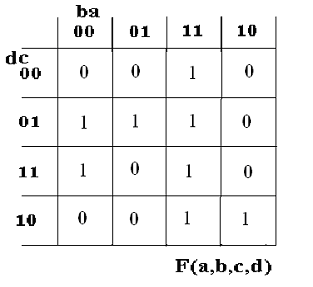
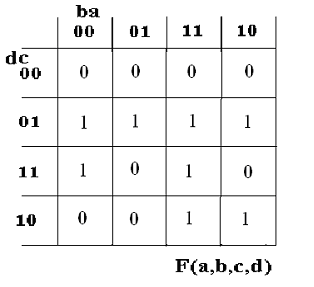
3 Zapisz funkcję w postaci sumy iloczynów oraz iloczynu

sum opisanej w siatce Karnaugha:

1 Przekształcić funkcję logiczną F do postaci sumy

iloczynów: F = a + b + c * d

2 Przekształcić funkcję logiczną F, aby zawierała jedynie

operatory sumy i negacji. Wykorzystać do tego prawa

d’Morgana F ( a, b, c, d ) = ( a * b + c) * d + b * d

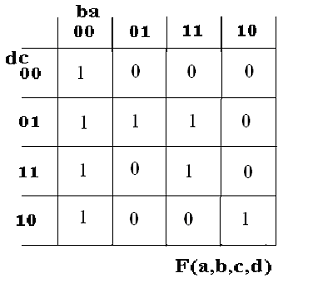
3 Zapisz funkcję w postaci sumy iloczynów oraz iloczynu

sum opisanej w siatce Karnaugha:

1 Przekształcić funkcję logiczną F do postaci iloczynu

sum: F = a * b + c + d

2 Przekształcić funkcję logiczną F, aby zawierała jedynie

operatory iloczynu i negacji. Wykorzystać do tego prawa

d’Morgana F ( a, b, c, d ) = ( a * b + c) * d + b * d

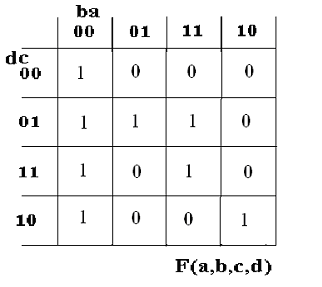
3 Zapisz funkcję w postaci sumy iloczynów oraz iloczynu

sum opisanej w siatce Karnaugha:

1 Przekształcić funkcję logiczną F do postaci iloczynu

sum: F = a * b + c * d

2 Przekształcić funkcję logiczną F, aby zawierała jedynie

operatory sumy i negacji. Wykorzystać do tego prawa

d’Morgana F ( a, b, c, d ) = ( a * b + c) * d + b * d

3 Zapisz funkcję w postaci sumy iloczynów oraz iloczynu

sum opisanej w siatce Karnaugha: