Jak bezpiecznie powiększyć fundusze na Półmetek ?
Tradycją braci studenckiej jest bal zwany Półmetkiem. Pewna grupa studentów dość niemrawo zabierała się za organizację takiego balu. Może nawet nie mieli ochoty na ten bal. Jednakże jeden z wykładowców dał im wyraźnie do zrozumienia, że łamanie wielowiekowej tradycji nie może mieć miejsca. To przesądziło, że wspomniana grupa raźniej zabrała się za sprawy organizacyjne.
W celu zwiększenia swoich możliwości w finansowaniu takiej imprezy postanowili zainwestować posiadany kapitał na giełdzie w akcje dwóch znanych browarów: Pianka i Kapsel. Zebrali informacje o kursach akcji obu spółek w kolejnych 20 sesjach.
nr notowania |
kursy akcji |
|
|
Pianka |
Kapsel |
1 |
204 |
256 |
2 |
236 |
269 |
3 |
244 |
256 |
4 |
214 |
274 |
5 |
204 |
279 |
6 |
246 |
313 |
7 |
251 |
273 |
8 |
220 |
307 |
9 |
204 |
302 |
10 |
237 |
267 |
11 |
210 |
315 |
12 |
212 |
287 |
13 |
219 |
302 |
14 |
239 |
294 |
15 |
219 |
254 |
16 |
234 |
271 |
17 |
205 |
297 |
18 |
238 |
261 |
19 |
210 |
279 |
20 |
251 |
282 |
Kolejny problem przed jakim stanęli wiązał się z podziałem posiadanego kapitału pomiędzy akcje obu spółek (jaka ma być struktura kapitałowa ich portfela ?). Było dla nich oczywistym, że muszą użyć portfela o minimalnym ryzyku (brać studencka ma na ogół ograniczone fundusze; chociaż patrząc na parking ...). Portfel taki można wyznaczyć m. in. budując i rozwiązując klasyczny model Markovitz'a. Słyszeli o takim modelu na jednym z wykładów. Jak to jednak bywa nie bardzo pamiętali już jak taki model wygląda (zgodnie z zasadą niemałej części braci studenckiej: „zdane i zapomniane”).
Przypomnijmy zatem model Markovitz'a. Znajdź udział kapitałowy (![]()
) każdej spółki w portfelu z akcjami n spółek o oczekiwanych stopach zwrotu (![]()
) w każdej tak, aby oczekiwana stopa zwrotu z portfela nie była mniejsza niż ![]()
oraz ryzyko portfela (mierzone wariancjami i kowariancjami stóp zwrotu ![]()
) było minimalne.
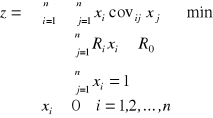
„Półmetkowicze” przyjęli 1%-owy oczekiwany zysk z portfela (![]()
=0,01). Należy teraz policzyć pozostałe parametry modelu Markovitz'a i ustalić skład portfela o najmniejszym ryzyku.
Model „półmetkowiczów” ma postać:
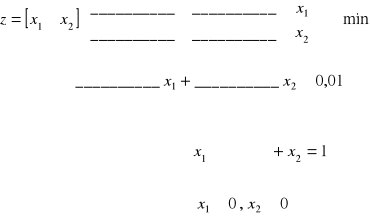
BROWARY (zadanie PK i zadanie Wolfe'a)
Zadanie PK (pierwotne)
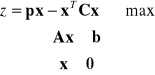
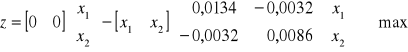
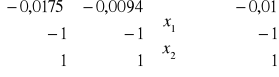
![]()
Ograniczenia w zadaniach pierwotnym i dualnym
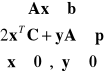
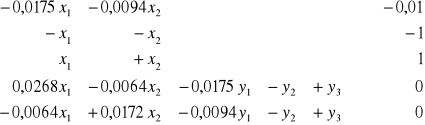
![]()
Zadanie Wolfe'a
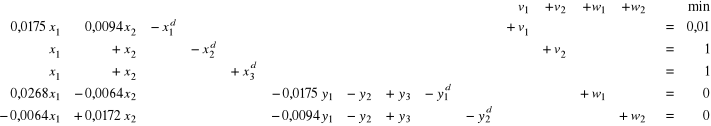
![]()
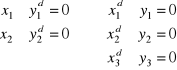
Rozwiązanie optymalne zadania PK : ![]()
Wyszukiwarka
Podobne podstrony:
zadanienia-programowanie, smf, , programowanie
WOLFEstud, Programowanie Kwadratowe - metoda Wolfe'a
ZADANIA Z PROGRAMOWANIA
zadania funkcja kwadratowa
Java Zadania z programowania z przykładowymi rozwiązaniami
6 2 Zadania programowania liniowego
AM, Liniowe zadanie decyzyjne, Model matematyczny zadania programowania liniowego
C++ Zadania z programowania z przykładowymi rozwiązaniami [PL]
274 zadania funkcje kwadratowe
Zadanie PROGRAMOWANIE, Informatyka
tp-zadania cz3, Szkoła, Programowanie, C++, Zadania z programowania cz.3
funkcje zadania gl kwadratowa, zadania z matematyki
C Zadania z Programowania
Stroop.eksp.zadanie, Programowanie procedur badawczych
Algorytmy-zadania, Programowanie, wykłady C++
C Zadania z programowania 9788324637072
27.2 wskazniki - zadania, Programowanie, Klasa III
Optymalizacja Cw 3 Zadanie programowania nieliniowego bez ograniczeń algorytmy optymalizacji lokaln
więcej podobnych podstron