Liniowe zadanie decyzyjne

Model matematyczny zadania - uproszczony opis zjawiska pozwalający na znalezienie przybliżonego rozwiązania problemu decyzyjnego.

W modelu matematycznym zadania liniowego występują:

1. zmienne decyzyjne - wielkości które mają być wyznaczone,

2. parametry zadania - wielkości dane,

3. warunki ograniczające - ograniczenia wynikające z treści zadania lub wiedzy ogólnej,

4. funkcja celu - funkcja określająca przydatność rozwiązania.

Model matematyczny w postaci normalnej LZD o
n niewiadomych i m ograniczeniach można zapisać następująco:

• Zmienne:
  x = [x₁, x₂, ..., x_n]

• Funkcja celu:
  F(x) = c₁x₁ + c₂x₂ + ... + c_nx_n Ⴎ max (min)

• Warunki ograniczające:
  a_1,1x₁ + a_1,2x₂ + ... + a_1,nx_n Ⴃ (Ⴓ, =) b₁
  a_2,1x₁ + a_2,2x₂ + ... + a_2,nx_n Ⴃ (Ⴓ, =) b₂
  ...
  a_m,1x₁ + a_m,2x₂ + ... + a_m,nx_n Ⴃ (Ⴓ, =) b_m

• Ograniczenia zmiennych:
  x_i Ⴓ (Ⴃ, bez ograniczenia) d_i, gdzie i=1, 2, ..., n

Istnieją dwa rodzaje rozwiązań ZPL:

1. rozwiązanie dopuszczalne - każde rozwiązanie spełniające wszystkie warunki ograniczające. Z zasady istnieje wiele rozwiązań dopuszczalnych,

2. rozwiązanie optymalne - to rozwiązanie dopuszczalne, które najlepiej spełnia funkcję celu (żadne rozwiązanie nie spełnia lepiej f. celu).

Zadanie 1. Zadanie produkcyjne (wybór asortymentu produkcji)

Zakład produkuje dwa wyroby, które są produkowane na dwóch obrabiarkach: O₁ i O₂ oraz na frezarce F. Czas pracy tych maszyn jest ograniczony i wynosi: O₁ - 33.000 h, O₂ - 13.000 h, F - 80.000 h. Zużycie czasu pracy maszyn na wyprodukowanie wyrobów przedstawia tabelka:

Maszyny	Zużycie czasu
		I	II
O1	3	1
O2	1	1
F	5	8

Zysk ze sprzedaży wyrobu I wynosi 1 zł, wyrobu II - 3 zł. Z analizy sprzedaży wynika, że wyrobu II nie można sprzedać więcej niż 7.000 szt.

Zaplanować produkcję tak, aby zysk był jak największy.

Model matematyczny

Zmienne decyzyjne:

x₁, x₂ - wielkość produkcji wyrobów I i II.

Funkcja celu:

Celem jest maksymalizacja zysku.

F=1x₁+3x₂ max

Ograniczenia:

3x₁+1x₂ <= 33.000 - ogr. dla O₁

1x₁+1x₂ <=13.000 - ogr. dla O₂

5x₁+8x₂ <=80.000 - ogr. dla F

x₂ <= 7.000 - ogr. dla wielkości sprzedaży

x₁ >= 0 - ogr. zmiennych

x₂ >=0

Rozwiązania

Rozwiązania dopuszczalne (np.):

x1=0 x2=0 F=0

x1=1 x2=1 F=4

x1=1 000 x2=1 000 F=4 000

x1=11 000 x2=0 F=11 000

x1=4 800 x2=7 000 F=25 800

Rozwiązanie optymalne:

x₁=4 800, x₂=7 000, F=25 800

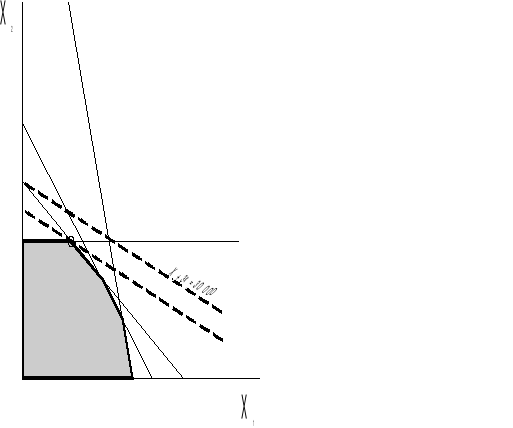
Metoda graficzna:

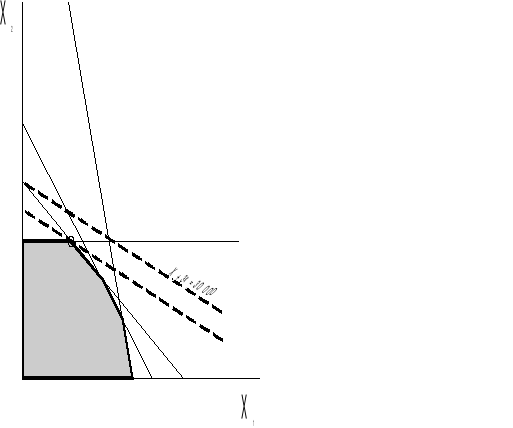
W układzie współrzędnych należy zaznaczyć poszczególne warunki ograniczające. Zbiór punktów należący do wszystkich ograniczeń jest zbiorem rozwiązań dopuszczalnych.

Rozwiązanie zadania liniowego zawsze leży na brzegu zbioru rozwiązań dopuszczalnych.

Zadanie 2. Zagadnienie diety

Dziecko potrzebuje tygodniowo co najmniej 120 mg witaminy A, 60 mg wit. D, 36 mg wit. C oraz 180 mg wit. E. Witaminy te są zawarte w dwóch produktach: P1 i P2. Ze względu na szkodliwość witaminy A można jej spożyć najwyżej 240 mg. Zawartość poszczególnych witamin w kilogramie produktów zawiera tabelka:

Witaminy	P1	P2
A	6	3
D	1	3
C	9	1
E	6	6
Cena	1,2 zł	1,8 zł

Ile należy zakupić produktów P1 i P2, aby dostarczyć dziecku odpowiednią ilość witamin oraz aby koszt zakupu był minimalny?

Model matematyczny

Zmienne decyzyjne:

x₁, x₂ - ilość kupionych produktów P1 i P2 (w kg).

Funkcja celu:

Celem jest minimalizacja kosztów zakupu.

F=1,2x₁+1,8x₂ min

Ograniczenia:

6x₁+3x₂ => 120 - ogr. dla wit. A

1x₁+3x₂ => 60 - ogr. dla wit. D

9x₁+x₂ => 36 - ogr. dla wit. C

6x₁+6x₂ => 180 - ogr. dla wit. E

6x₁+3x₂ <= 240 - ogr. dla wit. A

x₁ >= 0 - ogr. zmiennych

x₂ >=0

Rozwiązania

Rozwiązania dopuszczalne (np.):

x1 = 100 x2 = 500 F = 102

x1 = 15 x2 = 15 F = 45

x1 = 20 x2 = 30 F = 78

x1 = 20 x2 = 14 F = 49,2

Rozwiązanie optymalne:

x₁=15, x₂=15, F=45

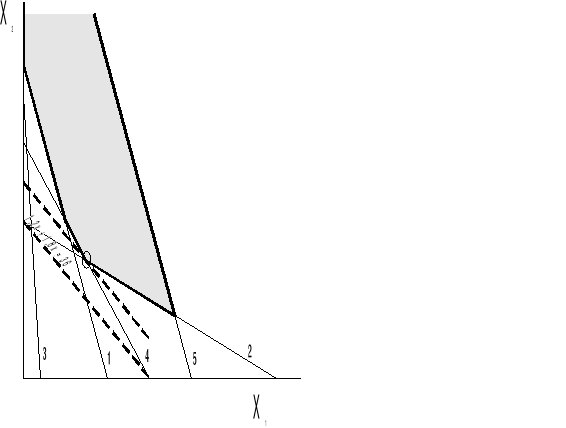
Rozwiązanie graficzne

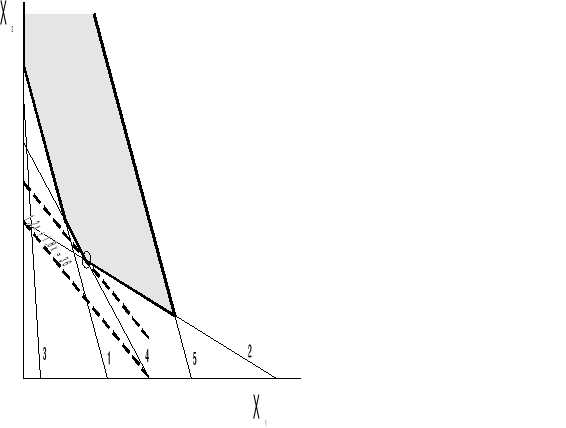
Zadanie 3. Zagadnienie diety

Dieta specjalna powinna dostarczyć do organizmu ponad 100 j. cukru i nie więcej niż 100 j. tłuszczo. Koszt zakupu produktu P1 wynosi 2 zł, produktu P2 - 5 zł. Zawartość obu składników w dwóch produktach przedstawia tabela:

Produkty	P1	P2
Cukier	10	10
Tłuszcz	20	25

Dobierz skład diety optymalnie pod względem kosztów.

Model matematyczny

Zmienne decyzyjne:

x₁, x₂ - ilość kupionych produktów P1 i P2 (w kg).

Funkcja celu:

Celem jest minimalizacja kosztów zakupu.

F=2x₁+5x₂ min

Ograniczenia:

10x₁+10x₂ => 100 - ogr. dla cukru

20x₁+25x₂ <= 100 - ogr. dla tłuszczu

x₁ >= 0 - ogr. zmiennych

x₂ >=0

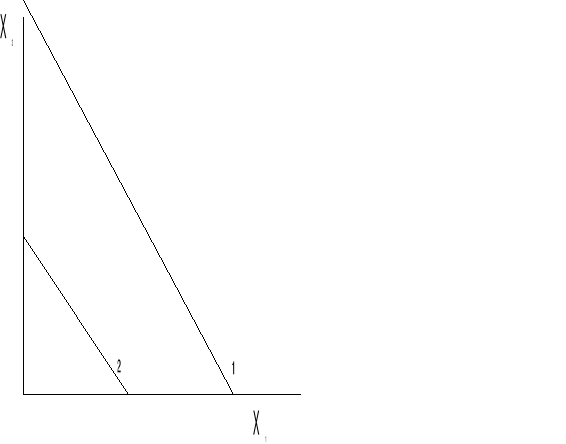
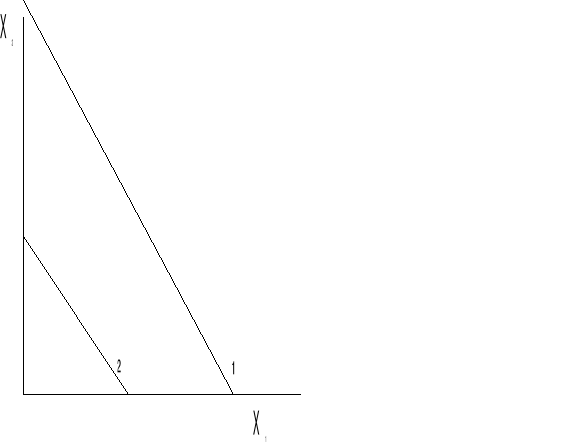
Rozwiązanie metodą graficzną

Brak rozwiązania dopuszczalnego.

Brak rozwiązania optymalnego.

Zadanie 4.

Przedsiębiorstwo produkuje dwa wyroby: A i B. Do produkcji tych wyrobów zużywa się trzech surowców: S1, S2 i S3, których dzienne zużycie jest limitowane. Ilość surowców niezbędnych do produkcji poszczególnych wyrobów pokazano w tabelce:

Surowce	A	B	Limit
S1	2	2	30
S2	3	2	36
S3	5	1	60

Dobrać wielkość produkcji, aby zysk był największy, jeżeli zysk ze sprzedaży wyrobu A wynosi 10 zł, a wyrobu B 10 zł.

Model matematyczny

Zmienne decyzyjne:

x₁, x₂ - wielkość produkcji wyrobów A i B.

Funkcja celu:

Celem jest maksymalizacja zysku.

F=10x₁+10x₂ max

Ograniczenia:

2x₁+2x₂ <= 30 - ogr. dla S1

3x₁+2x₂ <= 36 - ogr. dla S2

5x₁+x₂ <= 60 - ogr. dla S3

x₁ >= 0 - ogr. zmiennych

x₂ >=0

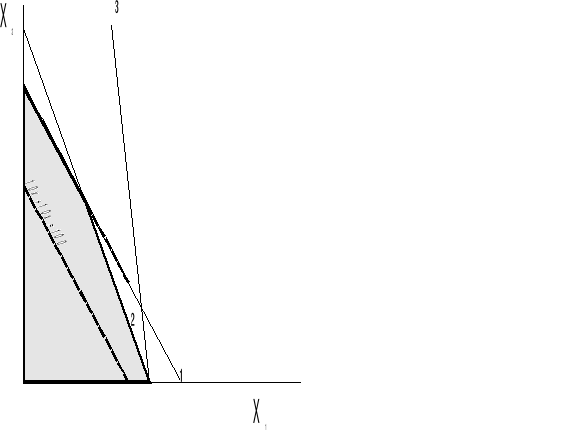
Rozwiązanie metodą graficzną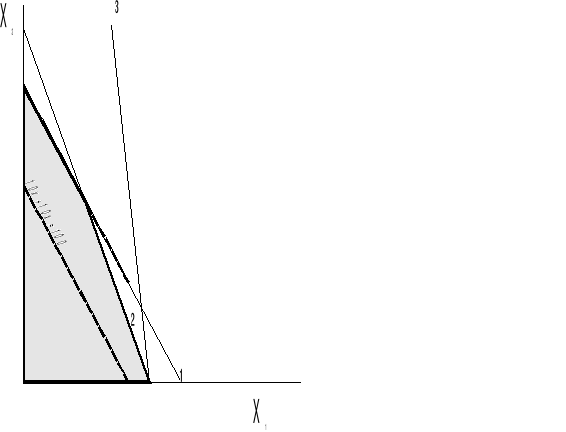

Rozwiązaniem optymalnym są wszystkie punkty należące do odcinka między wierzchołkami (0,15) i (6,9). Można je opisać wzorem: x₂=15-x₁, x₁∈<0;6>. Wynika z tego, że jest nieskończenie wiele rozwiązań optymalnych.

---