POLITECHNIKA WROCŁAWSKA POLITECHNIKA WROCŁAWSKA

WYDZIAŁ BL I W ZAKŁAD HYDRAULIKI

Ćwiczenie nr 4

Cel ćwiczenia.

Celem ćwiczenia jest doświadczalne i teoretyczne wyznaczenie kształtu swobodnej powierzchni cieczy w naczyniu cylindrycznym, wirującym wokół pionowej osi.

ROK AKADEMICKI 1996/'97 SZYMON GNACEK

ROK 3 SEM. 5 GR. 4

1.0 Wstęp teoretyczny.

Ciecz jest w równowadze względnej wówczas, gdy pozostaje ona w stanie spoczynku względem ścian poruszającego się naczynia. Występuje to wtedy, gdy naczynie porusza się ruchem jednostajnym, jednostajnie przyspieszonym prostoliniowym bądź ruchem jednostajnie obrotowym wokół osi pionowej. Efektem wizualnym równowagi względnej jest ukształtowanie swobodnej powierzchni cieczy. W naczyniu cylindrycznym ma ona kształt paraboloidy obrotowej, o osi pokrywającej się z osią obrotu naczynia.

Równanie opisujące kształt swobodnej powierzchni cieczy w naczyniu o promieniu R = D/2, wypełnionym do wysokości H cieczą i wirującym z prędkością kątową jest następujące

g - przyspieszenie ziemskie

2.0 Rysunek i opis stanowiska pomiarowego.

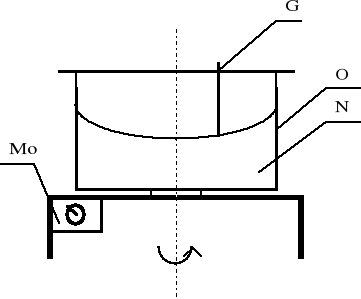
Stanowisko pomiarowe składa się z następujących elementów:

- naczynia cylidrycznego N,

- obudowy naczynia O,

- przyrządu do pomiaru paraboloidy G,

- urządzenia do regulacji i pomiaru prędkości obrotowej naczynia.

3.0 Opracowanie wyników pomiarów i obliczenia teoretyczne.

Składowe jednostkowe siły masowej

Po podstawieniu składowych sił masowych do różniczkowego równania powierzchni i scałkowaniu otrzymamy

Po przyjęciu punktu 0 na swobodnej powierzchni o współrzędnych

z = 0 , r = 0 to stała C = 0 i

4.0 Obliczenia

Krzywa teoretyczna

dla	ω=1,808	dla	ω=3,7
r	z	r	z
0	0	0	0
5	0,04	5	0,17
10	0,16	10	0,69
15	0,37	15	1,55
20	0,65	20	2,76
25	1,03	25	4,31
30	1,48	30	6,21
35	2,02	35	8,46
40	2,63	40	11,05
45	3,33	45	13,98

np.

5.0 Błędy pomiarów.

Dla ω = 1,808

r = 5 Δz = 0,00089 = 2,2 %

r = 10 Δz = 0,0032 = 2,03 %

r = 15 Δz = 0,0068 = 1,84 %

r = 20 Δz = 0,012 = 1,85 %

r = 25 Δz = 0,018 = 1,81 %

r = 30 Δz = 0,0268 = 1,81 %

r = 35 Δz = 0,037 = 1,80 %

r = 40 Δz = 0,047 = 1,80 %

r = 45 Δz = 0,059 = 1, 79 %

Jednostkami są centymetry.

Dla ω = 3,7

r = 5 Δz = 0,0046 = 2,7 %

r = 10 Δz = 0,017 = 2,4 %

r = 15 Δz = 0,037 = 2,4 %

r = 20 Δz = 0,065 = 2,4 %

r = 25 Δz = 0,101 = 3,4 %

r = 30 Δz = 0,145 = 2,3 %

r = 35 Δz = 0,196 = 2,3 %

r = 40 Δz = 0,256 = 3,3 %

r = 45 Δz = 0,323 = 2,3 %

6.0 Wnioski.

1. Krzywa empiryczna jest obarczona błędami pomiaru rzędnej Y , a także odciętej X , błędami odczytu z przyrządu pomiarowego , błędami wyniku przy wykonywaniu ćwiczenia.

2.Otrzymane wyniki równają się sobie. Paraboloidy empiryczne i teoretyczne nie równają się sobie , jest to wynikiem błędów pomiarowych , które wpłynęły na błędy metody empirycznej i teoretycznej. W obydwu wypadkach krzywa empiryczna znajduje się pod krzywą teoretyczną co może być wynikiem niedokładności pomiarze rzędnej Y przy ustalonym X. Porównując wykresy teoretyczne i empiryczne obu doświadczeń można dojść do wniosku, że krzywe mają podobny charakter. W miarę oddalania się od środka wirującego naczynia, krzywe teoretyczna i empiryczna zbliżają się do siebie.

3.Zestawiając ze sobą wykresy uzyskane w obu doświadczeniach zauważamy, że im mniejsza prędkość kątowa tym wykres jest bardziej płaski.

4.Przy badaniu równowagi względnej cieczy przy dwóch różnych prędkościach obrotowych cieczy pokazane są dwa różne kształty paraboloid obrotowych. Kształt więc zależy od prędkości. Przy przejściu punktu 0 na swobodnej powierzchni równanie paraboloidy przedstawia się . W doświadczeniu krzywa teoretyczna pokryje się z krzywą empiryczną.

KRZYWA PARABOIDALNA ω = 3,7

---