ĆWICZENIA LABORATORYJNE Z FIZYKI
S P R A W O Z D A N I E
Widmem absorpcji nazywa się w spektroskopii zależność współczynnika absorpcji od długości fali , (). Jak wynika ze wzoru:
A() = () c l
Wartość absorbancji A dla danej długości fali jest iloczynem wartości współczynnika dla tej samej długości fali i stałej wartości c l, która nie zależy od . Stąd wniosek, że wykres zależności A() ma taki sam charakter (ilość pasm absorpcji, ich kształt) i dostarcza podobnych informacji jak wykres funkcji (). Wykres zależności A() można traktować również jako widmo absorpcji. Pomiaru widma absorpcji dokonuje się za pomocą spektrofotometru. Kolejno dla poszczególnych długości fal . odczytujemy na skali spektrofotometru absorbancję A i transmitancję T w zakresie ultrafioletu i w dziedzinie widzialnej lub tylko w dziedzinie widzialnej. Podczas pomiaru absorbancji roztworów jako natężenie światła I0 przyjmuje się natężenie światła przechodzącego przez kuwetę z rozpuszczalnikiem. W ten sposób eliminuje się osłabienie wiązki w wyniku załamania i rozpraszania światła w kuwecie i rozpuszczalniku. Widmo absorpcji mierzymy punktowo za pomocą spektrofotometru VSU2P lub w sposób ciągły, z automatycznym zapisem za pomocą spekordu UV-VIS oraz spektrofotometru M40 z automatycznym wydrukiem wartości absorbancji.
Fotoluminescencja. Emisja światła przez zbiór cząsteczek, które znalazły się w energetycznym stanie wzbudzonym w wyniku absorpcji światła nazywa się fotoluminescencją. Jest to emisja spontaniczna. Średni czas życia (istnienia) cząsteczki w stanie wzbudzonym ≥10-9 s.
Weźmy pod uwagę wieloatomowe cząsteczki wybranego związku organicznego wykazującego fotoluminescencję. Niech związek będzie rozpuszczony w rozpuszczalniku nieluminezującym. Aby pobudzić substancję do świecenia należy oświetlić kuwetę z roztworem wiązką światła o długościach fal z zakresu widma absorpcji charakterystycznego dla tego związku. Oddziaływanie światła z cząsteczkami substancji należy rozpatrywać na podstawie teorii kwantowej. Zgodnie z tą teorią cząsteczki, po pochłonięciu odpowiedniego kwantu świetlnego hv, z zakresu widma widzialnego lub ultrafioletu, znajdują się w elektronowym stanie wzbudzonym na odpowiednim poziomie oscylacyjnym. Jest to stan energetycznie niestabilny S, w jakim znalazła się cząsteczka w wyniku optycznego wzbudzenia. Cząsteczka stara się więc oddać nadmiar energii, aby przejść do stanu stacjonarnego, odpowiadającego minimum energii w danych warunkach fizykochemicznych, czyli do stanu podstawowego S0. Z energetycznego stanu wzbudzonego S do stanu podstawowego S0 cząsteczki mogą przejść w różny sposób. Procesy absorpcji i emisji światła oraz de aktywacji energii optycznego wzbudzenia można zapisać następująco:
S0 + hva → S absorpcja
gdzie:
va - częstotliwość światła absorbowanego,
h - stała Plancka
I S → S0 + Q rozpraszanie energii
II S + W0 → S0 + W wygaszanie
W0, W - stany energetyczne cząsteczki wygaszacza, odpowiednio w stanie podstawowym i wzbudzonym.
III S → S0 (P) fotoreakcje
Fotoluminescencja
IV S → S0 + hvf fluorescencja
S1 → T1
V T1→S1 fluorescencja długożyciowa
S1 → S0 + hvdf
S1 → T1
VI fluorescencja
T1 → S0 + hvfosf
Cząsteczka w elektronowym stanie wzbudzonym S może przekazać cząsteczkom otaczającym, np. cząsteczkom rozpuszczalnika, nadmiar energii jako ciepło (na sposób ciepła) w ilości Q i przejść do stanu podstawowego S0. Nastąpi wtedy tzw. rozpraszanie energii (zależność I). Jeżeli w bliskim otoczeniu cząsteczki S znajdzie się cząsteczka innej substancji w elektronowym stanie podstawowym W0, która może przejąć cały nadmiar energii cząsteczki w stanie S, to następuje przekazanie energii. Cząsteczka wygaszacza W0 przechodzi do stanu wzbudzonego W. Proces ten nazywa się wygaszaniem fluorescencji (wygaszanie świecenia) lub rezonansowym przekazywaniem energii - zależność II. Nadmiar energii w stanie wzbudzonym może być "wykorzystany" przez cząsteczkę na fotoreakcję, w której wyniku powstają fotoprodukty S0 (P) zależność III.
Jeżeli powyższe przypadki deaktywacji energii optycznego wzbudzenia są mało prawdopodobne, to cząsteczka może wyemitować nadmiar energii w postaci kwantu hvf (vf - częstotliwość światła emitowanego). Jest to jeden z przypadków fotoluminescencji. Ten rodzaj fotoluminescencji nazywa się fluorescencją (zależność IV). Substancjami fluoryzującymi są często barwniki organiczne w roztworach ciekłych.
W odpowiednich warunkach cząsteczka może przejść ze stanu wzbudzonego S1 do stanu metastabilnego (trójkowego, długożyciowego) T1, charakteryzującego się wyraźnie dłuższym czasem życia niż stan S1, Kosztem energii termicznej cząsteczek otaczających, może nastąpić powrót cząsteczki ze stanu T1 do stanu S1 i dopiero wtedy nastąpi przejście do stanu podstawowego S0, połączone z emisją promieniowania zwaną fluorescencją długożyciową lub opóźnioną (zależność V). Powrót ze stanu długożyciowego T1 do stanu S1 może być utrudniony na przykład przez obniżenie temperatury lub "usztywnienie" środowiska. Wtedy następuje emisyjne przejście ze stanu T1 do stanu S0 i mamy do czynienia ze świeceniem zwanym fosforescencją (zależność VI).
Ze względu na mechanizm świecenia możemy więc fotoluminescencję cząsteczek podzielić na trzy rodzaje: fluorescencję, która zachodzi tylko przy udziale stanu singletowego S; fluorescencję długożyciową i fosforescencję, w których bierze udział stan metatrwały T.
Fluorescencja. W celu wyjaśnienia mechanizmu fluorescencji i poznania właściwości spektralnych światła emitowanego, należy rozpatrywać rozszerzony obraz stanów energetycznych zbioru cząsteczek. Mogą to być np. cząsteczki barwnika rozpuszczonego w wodzie. Aby nastąpiła fluorescencja, układ musi być wzbudzony światłem o częstotliwości z zakresu widma absorpcji barwnika. Cząsteczki absorbują różne kwanty energii, czyli znajdą się w różnych oscylacyjnych i rotacyjnych stanach energetycznych danego, elektronowego stanu wzbudzonego. Bredni czas przebywania cząsteczki w elektronowym stanie wzbudzonym, czas życia cząsteczki w elektronowym stanie wzbudzonym, jest rzędu 10-9 s.
W tym przedziale czasowym cząsteczki przekazują otoczeniu, w sposób bezemisyjny, nadmiar energii oscylacyjnej i rotacyjnej w stanie wzbudzonym S1 oraz, zazwyczaj, przechodzą z wyższych elektronowych stanów wzbudzonych do stanu S1. W wyniku tego, przed aktem emisji, wszystkie cząsteczki zdolne do fluorescencji znajdą się na zerowym poziomie oscylacyjnym pierwszego elektronowego stanu wzbudzonego S1 (reguła Kashy). Podczas aktu emisji cząsteczki przechodzą do różnych stanów oscylacyjnych i rotacyjnych elektronowego stanu podstawowego S0. Zgodnie z zasadami mechaniki kwantowej zachodzi emisja różnych kwantów świetlnych z różnym prawdopodobieństwem, czyli natężenie emitowanego światła o różnych długościach fal jest różne. Zależność natężenia fluorescencji F od częstotliwości v lub długości fali emitowanej ![]()
nazywa się widmem fluorescencji F = f(). Widmo fluorescencji występuje w postaci pasma, które ma kształt podobny do krzywej Gaussa, przy czym od strony małych częstotliwości (dużych długości fal) zaznacza się wyraźne rozszerzenie pasma fluorescencji. Emitowane kwanty są zazwyczaj mniejsze od kwantów absorbowanych. Widmo fluorescencji jest więc przesunięte w stronę fal dłuższych w stosunku do najbardziej długofalowego pasma absorpcji. Tę prawidłowość zapisał Stokes w następującej postaci:
f > a
gdzie:
f - długość fali odpowiadająca maksimum pasma fluorescencji
a - długość fali odpowiadająca maksimum pasma absorpcji.
W spektralnej analizie ilościowej wykorzystuje się zależność natężenia fluorescencji (F) od stężenia substancji fluoryzującej w roztworze. Wartość natężenia fluorescencji zależy od ilości światła zaabsorbowanego (P) oraz od kwantowej wydajności fluorescencji ().
F = k P
gdzie:
k - stała układu pomiarowego.
Wydajność kwantowa fluorescencji jest to stosunek liczby kwantów emitowanych do liczby kwantów absorbowanych przez substancję fluoryzującą w danych warunkach fizykochemicznych. Zgodnie z prawem absorpcji, ilość światła zaabsorbowanego P przez daną substancję w roztworze można wyrazić wzorem:
P = I0 - I
gdzie:
I = I0 e- c l
stąd
P = I0 (1 - e- c l)
gdzie:
I0 - natężenie światła padającego na badaną próbkę,
I - natężenie światła przechodzącego,
- współczynnik absorpcji,
c - stężenie substancji absorbującej,
l - grubość warstwy.
W praktyce spektroskopowej wykładnik potęgowy - c l dla małych stężeń jest zazwyczaj mały. Po rozwinięciu ex, gdzie: x = - c l, na szereg potęgowy mamy:
![]()
Wyraz trzeci i dalsze wyrazy w szeregu można pominąć jako bardzo małe, stąd
e- c l = 1 - c l
Po wprowadzeniu molowego współczynnika absorpcji = lge, otrzymuje się:
P = 2,3 I0 c l
Wyrażenie F = k P na natężenie światła fluorescencji F dla małych stężeń substancji fluoryzującej przyjmie więc postać:
F = 2,3 k I0 c l
Stąd wniosek, że w danych warunkach fizykochemicznych dla danej substancji, natężenie fluorescencji F jest wprost proporcjonalne do stężenia c substancji fluoryzującej w roztworze:
![]()
Zależność ta jest wykorzystywana w analityce chemicznej do ilościowego oznaczania substancji. Jeżeli badana substancja wykazuje fluorescencję w roztworze, a rozpuszczalnik oraz ewentualne domieszki nie fluoryzują, to fluorescencyjna metoda wyznaczania stężenia substancji w roztworze polega na porównaniu natężenia fluorescencji badanego roztworu z natężeniem fluorescencji roztworu tej samej substancji o znanym stężeniu. W tym celu należy zbadać zależność natężenia fluorescencji F od stężenia c badanej substancji w roztworach wzorcowych. Stosuje się roztwory wzorcowe o kilku różnych stężeniach w zakresie małych stężeń. Zakres ten można wyznaczyć doświadczalnie dla każdej substancji w danym rozpuszczalniku. Zasadą przygotowania roztworów wzorcowych jest, by badana substancja w roztworach wzorcowych znajdowała się w takich samych warunkach fizykochemicznych jak w roztworze badanym. Jeżeli warunek ten jest spełniony, to wykres funkcji F = f(c), czyli tzw. krzywa wzorcowa, będzie linią prostą. Po przygotowaniu krzywej wzorcowej należy zmierzyć natężenie fluorescencji roztworu badanego w tych samych warunkach wzbudzenia i z krzywej wzorcowej odczytać stężenie badanej substancji w roztworze. Podczas badania fluorescencji barwników wzbudzamy je zazwyczaj w zakresie najbardziej długofalowego pasma absorpcji, które leży w przedziale widzialnym widma. Jak wynika ze wzoru:
F = 2,3 k I0 c l
natężenie fluorescencji dla danej próbki zależy od natężenia światła wzbudzającego I0 oraz molowego współczynnika absorpcji . Aby uzyskać wzbudzenie najbardziej efektywne, należy badany roztwór oświetlić światłem o długości fali zbliżonej do maksimum pasma absorpcji, tak by iloczyn I0 osiągnął wartość maksymalną. Zakres wzbudzenia, który spełnia ten warunek, można określić z zależności natężenia fluorescencji od długości fali wzbudzającej wzb. Zależność F(wzb) wyznacza się doświadczalnie. Jest to widmo wzbudzenia.
Metoda pomiaru fluorescencji. Do badania fluorescencji służy układ przedstawiony na rysunku 6.24. Fluorescencję wzbudzamy światłem ze źródła (Z), przechodzącym przez monochromator (M). Światło o danej długości fali pada na kuwetę (K)
OBLICZENIA I POMIARY:
Do ćw. 74
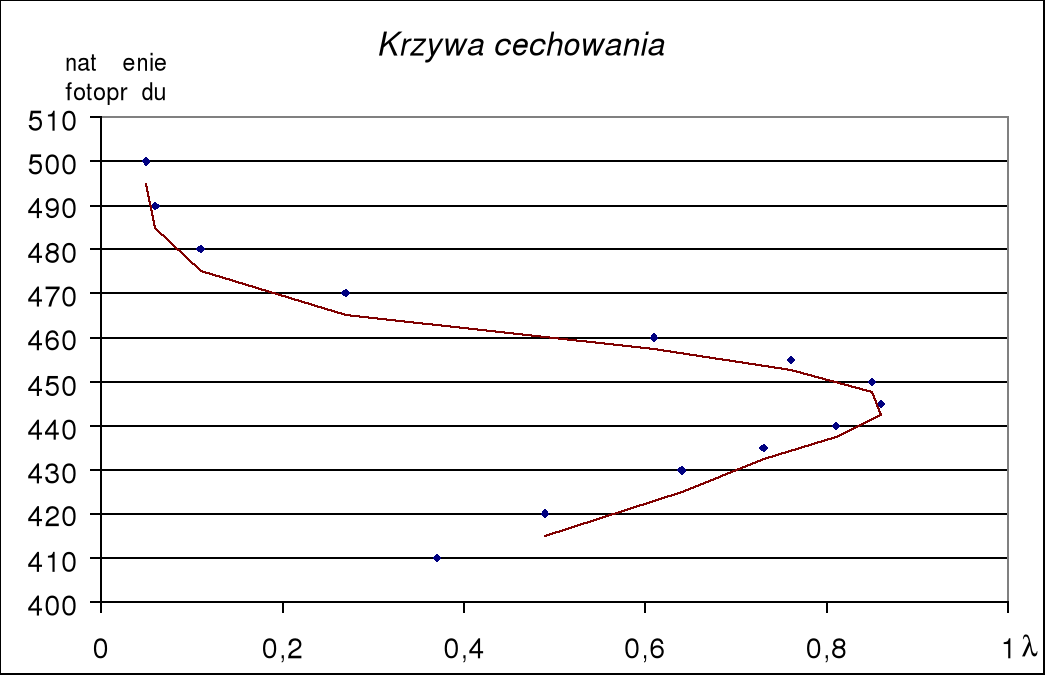
wzb (nm) |
410 |
420 |
430 |
435 |
440 |
445 |
450 |
455 |
460 |
470 |
480 |
490 |
500 |
Natężenie fotoprądu (i) |
0,37 |
0,49 |
0,64 |
0,73 |
0,81 |
0,86 |
0,85 |
0,76 |
0,61 |
0,27 |
0,11 |
0,06 |
0,05 |
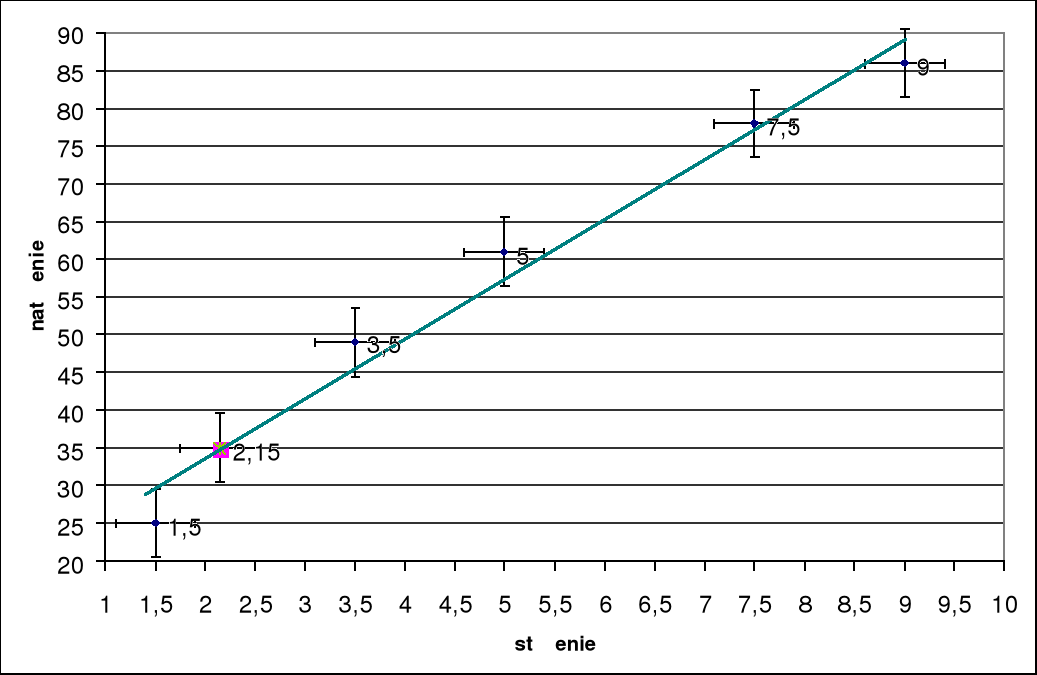
Lp. |
c (M/l) |
i (A) |
cx |
1 2 3 4 5 6 |
1,5 ∙ 10-6 3,5 ∙ 10-6 5 ∙ 10-6 7 ∙ 10-6 9 ∙ 10-6 Cx = 2 ∙ 10-6 |
25 49 61 78 86 35 |
Cx = 2 ∙ 10-6 |
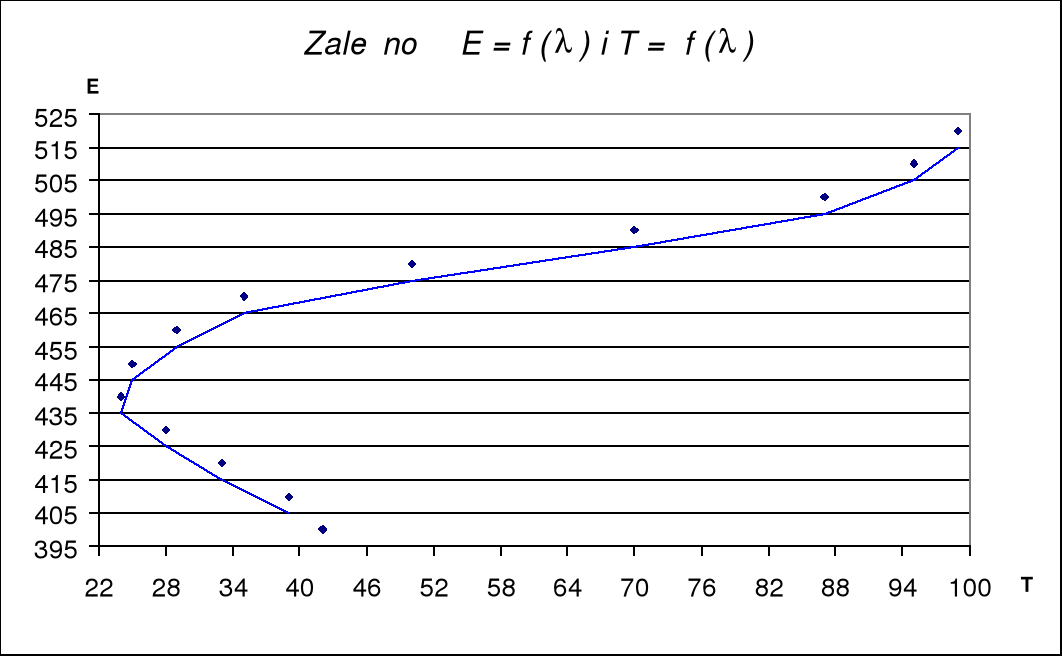
Do ćw. 57
L.p. |
(nm) |
E (A) |
T |
1 |
400 |
0,375 |
42 |
2 |
410 |
0,41 |
39 |
3 |
420 |
0,49 |
33 |
4 |
430 |
0,55 |
28 |
5 |
440 |
0,62 |
24 |
6 |
450 |
0,6 |
25 |
7 |
460 |
0,53 |
29 |
8 |
470 |
0,45 |
35 |
9 |
480 |
0,305 |
50 |
10 |
490 |
0,15 |
70 |
11 |
500 |
0,06 |
87 |
12 |
510 |
0,02 |
95 |
13 |
520 |
0,005 |
99 |
wartość najwyższa 440 |
445 |
0,62 |
24 |
C [mol / l] |
E |
T |
1,5 ∙ 10-6 3,5 ∙ 10-6 5 ∙ 10-6 7 ∙ 10-6 9 ∙ 10-6 Cx = 2 ∙ 10-6 |
0,09 0,21 0,29 0,42 0,53 0,17 |
81 62 51 37 30 68 |
Obliczenie wartości niepewności:
Ćw. 57
Dane:
Y = Ax + B
A = 57250
B = 0,004601
Y = 0,17
ΔA = 1726
ΔB = 0,01026
ΔY = ΔI = 0,001
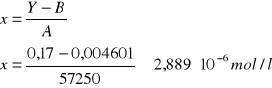
Niepewność pomiaru:
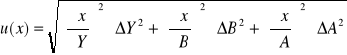
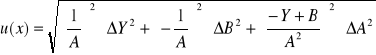
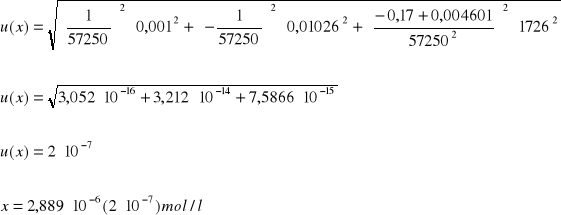
Ćw. 74
Dane:
Y = Ax + B
A = 7942000
B = 17,71
Y = 35
ΔA = 724000
ΔB = 4,304
ΔY = ΔI = 0,001
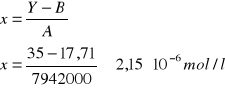
Niepewność pomiaru:
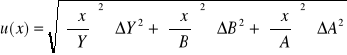
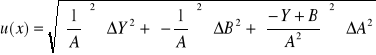
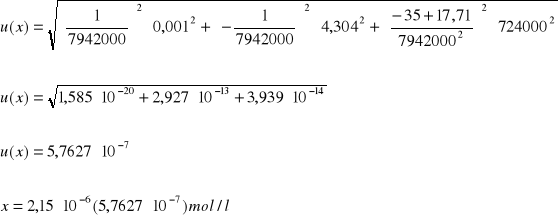
Wyszukiwarka
Podobne podstrony:
FIZYKA-sprawozdania, 57,74
57 74
57,74
57,74
57,74
57 74 schola
74 Nw 11 Obwody drukowane
74 Sliding Roof Convertible
cwiczenie 57
OiM Dywizja Georga von Derfflingera 1656 57
pomine VI 57
74 76
1 (57)
2015 08 20 08 13 57 01
01 1996 57 60
57 58
kratownica belka 57
57 60
więcej podobnych podstron