POLITECHNIKA LUBELSKA

WYDZIAŁ ELEKTRYCZNY

METODY NUMERYCZNE

Temat:

INTERPOLACJA

1. Sformułowanie zagadnienia interpolacji

2. Interpolacja za pomocą wielomianów algebraicznych

Opracowanie:

Arkadiusz Pieczykolan ED 7.5

Lublin 1995

I. Sformułowanie zagadnienia interpolacji

Wiele zjawisk fizycznych jest opisywanych przez funkcje, których dokładnie nie znamy. Często jednak potrafimy obliczyć lub zmierzyć wartości tych funkcji lub ich pochodnych dla określonych wartości argumentu. Przykładowo, w określonych chwilach czasu możemy mierzyć położenie, prędkość i przyspieszenie poruszającego się punktu. W praktyce najważniejsze jest to, że informacja o funkcji dana jest poprzez wartości i wartości kolejnych pochodnych w ustalonych punktach. Z własności fizycznych wiadomo też nieraz jaki jest w przybliżeniu charakter funkcji f np. że jest to wielomian niskiego stopnia, funkcja wykładnicza, okresowa itp.

Zagadnienie interpolacji można sformułować następująco:

Na przedziale <a;b> danych jest n+1 różnych punktów x₀, x₁, ..., x_n, zwanych węzłami interpolacji, oraz wartości pewnej funkcji y=f(x), zwanej funkcją interpolowaną, w tych punktach:

f(x₀)=y₀, f(x₁)=y₁, ..., f(x_n)=y_n

Zadaniem interpolacji jest wyznaczenie przybliżonych wartości funkcji w punktach nie będących węzłami oraz oszacowanie błędu tych przybliżeń. W tym celu należy znaleźć funkcję F(x), zwaną funkcją interpolującą, która w węzłach interpolacji przyjmuje takie same wartości co funkcja f(x) (patrz rys. nr 1).

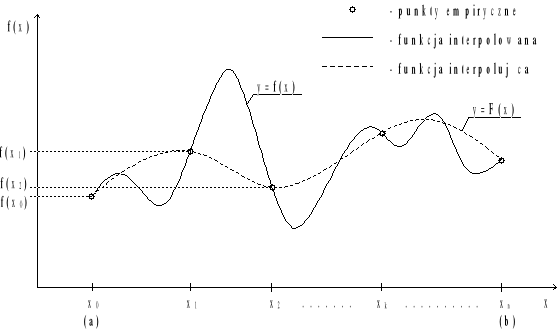
Rys. nr 1 Zagadnienie interpolacji

Można powiedzieć, że interpolacja jest w pewnym sensie zadaniem odwrotnym do tablicowania funkcji. Przy tablicowaniu mając analityczną postać funkcji budujemy tablicę wartości, przy interpolacji natomiast na podstawie tablicy wartości funkcji określamy jej postać analityczną.

Funkcji interpolującej poszukuje się najczęściej jako funkcji pewnej określonej postaci. Dokładniej zajmiemy się tutaj interpolacją wielomianami algebraicznymi, wielomianami trygonometrycznymi i funkcjami sklejanymi. Dla tych klas funkcji zapamiętanie pełnej informacji o nich (np. współczynników wielomianu) nie wymaga dużego obciążenia pamięci maszyny cyfrowej. Ponadto można łatwo wykonywać na tych funkcjach różne działania takie jak np. dodawanie, mnożenie, różniczkowanie czy całkowanie.

Zastosowanie do obliczeń bardzo szybkich maszyn cyfrowych o dużych pamięciach spowodowało, że interpolacja, będąca niegdyś jedną z podstawowych metod numerycznych, straciła nieco na znaczeniu. Obecnie albo stosuje się proste metody, jak interpolacja liniowa czy kwadratowa, albo też bardziej złożone, wymagające użycia maszyny cyfrowej, jak np. interpolacja za pomocą funkcji sklejanych.

Ponieważ wzory interpolacyjne są punktem wyjścia do wprowadzenia wielu metod stosowanych w innych działach metod numerycznych (różniczkowanie numeryczne, numeryczne rozwiązywanie równań różniczkowych) warto zapoznać się z podstawowymi wzorami interpolacyjnymi.

Najważniejsze zastosowania interpolacji to przybliżone obliczanie całek, rozwiązywanie zagadnień różniczkowych zwyczajnych i równań nieliniowych.

Interpolacja a ekstrapolacja

Z interpolacją mamy do czynienia, gdy wyznaczamy wartość funkcji w wybranym punkcie x, który leży wewnątrz rozpatrywanego przedziału <a;b> (x∈<a;b>).

Z ekstrapolacją mamy do czynienia, gdy wyznaczamy wartość funkcji w wybranym punkcie x, który leży na zewnątrz rozpatrywanego przedziału <a;b> (x∉<a;b>).

Błąd, z jakim potrafimy wyznaczyć wartość funkcji w tym punkcie x jest większy przy ekstrapolacji. Ekstrapolacja jest procesem wewnętrznie bardziej niedokładnym niż interpolacja. Korzystając z ekstrapolacji, aby zmniejszyć błąd, punkt x powinien leżeć możliwie jak najbliżej przedziału rozpiętego na węzłach.

Ogólnie stwierdzając, interpolacja jest bardziej praktyczna i powszechna.

II. Interpolacja za pomocą wielomianów algebraicznych

1. Postacie wielomianu i obliczanie jego wartości

Najczęściej wykorzystywane przedstawienie wielomianu to przedstawienie w postaci naturalnej tzw. rozwinięcia potęgowego:

Dla reprezentacji wielomianu w tej postaci potrzeba tylko n+1 miejsc pamięci na zapamiętanie współczynników a_k (k=0, 1, ..., n). Postać naturalna jest wygodna np. przy obliczaniu całek czy pochodnych wielomianu, a także przy wykonywaniu działań arytmetycznych na wielomianach.

Do obliczania wartości wielomianu w(x) danego w postaci naturalnej w ustalonym punkcie x (x≠0) służy algorytm Hornera obliczania wartości wielomianu w(x). Po przedstawieniu w(x) w zmienionej postaci:

w(x)=(. . .(a_n⋅x+ a_n-1)⋅x+. . .+a₁)⋅x+a₀

mamy:

w_n=a_n

w_i=w_i+1⋅x+a_i dla i=n-1, n-2, ..., 0

Oczywiste jest, że w(x)=w₀.

Inna użyteczna postać wielomianu to postać Newtona:

gdzie:

p₀(x)=1

p_k(x)=(x-x₀)⋅(x-x₁)⋅. . .⋅(x-x_k-1) dla k=1, 2, ..., n

a x₀, x₁, ..., x_n są danymi liczbami.

2. Wielomiany interpolacyjne

2.1. Jednoznaczność rozwiązania zagadnienia interpolacyjnego

Rzeczą bardzo ważną jest, aby istniała dokładnie jedna funkcja interpolująca znaleziona przy użyciu interpolacji.

Szukamy wielomianu W_n(x), stopnia co najwyżej n, spełniającego warunki:

y₀=f(x₀), y₁=f(x₁), ..., y_n=f(x_n) (1)

Jednoznaczność tak sformułowanego zagadnienia interpolacyjnego rozstrzyga poniższe twierdzenie.

Twierdzenie

Istnieje dokładnie jeden wielomian interpolacyjny stopnia co najwyżej n (n≥0), który w punktach x₀, x₁, ..., x_n przyjmuje wartości y₀, y₁, ..., y_n.

Dowód

Przyjmijmy, że węzły interpolacji są rozmieszczone w zupełnie dowolny sposób w przedziale <a;b>. Mamy n+1 węzłów, w których są znane wartości pewnej funkcji y=f(x). Szukany wielomian zapisujemy w postaci:

W_n(x)=a₀+a₁⋅x+a₂⋅x²+. . .+a_n⋅xⁿ (2)

Korzystając z warunków (1) otrzymujemy układ n+1 równań z n+1 niewiadomymi współczynnikami a₀, a₁, ..., a_n:

a₀+a₁⋅x₀+a₂⋅x₀²+. . .+a_n⋅x₀ⁿ=y₀

a₀+a₁⋅x₁+a₂⋅x₁²+ . ..+a_n⋅x₁ⁿ=y₁

. . . . . . . . . . . . . . . . . . . . .

a₀+a₁⋅x_n+a₂⋅x_n²+. . .+a_n⋅x_nⁿ=y_n

Macierz współczynników tego układu ma postać:

a wyznacznik D macierzy A (zwany wyznacznikiem Vandermonde'a):

Przy założeniach, że x_i≠x_j dla i≠j zawsze .

Zatem układ ma dokładnie jedno rozwiązanie, a wartości a_i według twierdzenia Cramera są określone wzorem:

(3)

gdzie D_ij (j=0, 1, 2, ..., n) są kolejnymi dopełnieniami algebraicznymi elementów i-tej kolumny wyznacznika D.

2.2. Wielomian interpolacyjny Taylora

W zagadnieniu interpolacyjnym Taylora wykorzystywana jest wartość funkcji i jej kolejnych pochodnych w jednym punkcie.

Jeżeli funkcja rzeczywista jest określona w pewnym otoczeniu punktu x₀∈R oraz ma n-tą pochodną w tym otoczeniu, to wielomian algebraiczny:

x∈R, nazywa się wielomianem Taylora dla funkcji f(x). Jest on jednoznaczny.

przykład

Podać dla funkcji f(x)=sin(x) kilka wielomianów interpolacyjnych Taylora dla n=1, 2, 3, 4, 5, 6, 7, 8 w punkcie x₀=0:

Graficzne przedstawienie kolejnych przybliżeń funkcji f(x)=sin(x) wielomianami Taylora zawiera poniższy rysunek:

2.3. Wielomian interpolacyjny Lagrange'a

W zagadnieniu interpolacyjnym Lagrange'a wykorzystywane są tylko wartości funkcji w różnych punktach.

Zadanie interpolacyjne Lagrange'a polega na znalezieniu dla danej funkcji f wielomianu W_n(x) stopnia nie wyższego niż n, którego wartości w n+1 punktach są takie same jak wartości interpolowanej funkcji f, tzn.

W_n(x_i)=f(x_i) dla i=0, 1, ..., n

Odnosi się to wszystko zarówno do przypadku funkcji f i węzłów interpolacyjnych rzeczywistych jak i zespolonych.

Podstawiając (3) do (2) i grupując razem te składniki, w których występują jednakowe y_j, otrzymujemy:

W_n(x)=y₀⋅Φ₀(x)+y₁⋅Φ₁(x)+. . .+y_n⋅Φ_n(x) (4)

gdzie funkcje Φ₀(x), Φ₁(x), ...,Φ_n(x) są wielomianami stopnia co najwyżej n.

Zakładamy, że węzły są rozmieszczone w dowolny sposób. Poszukujemy wielomianu W_n(x) stopnia co najwyżej n określonego wzorem (4).

Dla każdego i=0, 1, ..., n zachodzi zależność

W_n(x_i)=y₀⋅Φ₀(x_i)+y₁⋅Φ₁(x_i)+. . .+y_n⋅Φ_n(x_i)

skąd wynika, że

Aby określić funkcję Φ_j(x) należy znaleźć wielomian stopnia n, który w punktach x₀, x₁, ..., x_j-1, x_j+1, ..., x_n jest tożsamościowo równy zeru, a w punkcie x_j równa się jedności. Stąd

Φ_j(x)=λ⋅(x-x₀)⋅(x-x₁)⋅. . .⋅(x-x_j-1) (x-x_j+1)⋅. . .⋅ (x-x_n) λ - stała (5)

a ponieważ Φ_j(x_i)=1

1=λ⋅(x_j-x₀)⋅(x_j-x₁)⋅. . .⋅(x_j-x_j-1) (x_j-x_j+1)⋅. . .⋅ (x_j-x_n) (6)

Po wyrugowaniu stałej λ ze wzorów (4) i (5) otrzymujemy:

Zatem W_n(x) ma postać:

gdzie y_j=f(x_j).

Przyjmując oznaczenia:

ω_k(x)=(x-x₀)⋅(x-x₁)⋅. . .⋅(x-x_n)

ω_n′(x_j) - wartość pochodnej wielomianu W_n(x) w punkcie x_j będącym zerem tego wielomianu

mamy ostateczny wzór:

(7)

Wzór ten nazywa się wzorem interpolacyjnym Lagrange'a funkcji f opartym na węzłach x₀, x₁, ..., x_n. Wielomian ten jest wielomianem stopnia co najwyżej n i jest jednoznacznym rozwiązaniem zadania interpolacyjnego Lagrange'a dla dowolnego wyboru n+1 węzłów interpolacji.

przykład

a) Znaleźć wielomian interpolacyjny, który w punktach -2, 1, 2, 4 przyjmuje wartości 3, 1, -3, 8.

Stosując wzór Lagrange'a (7) dla n=3 mamy:

b) Znaleźć wielomian interpolacyjny Lagrange'a dla funkcji w punktach x₀=0, x₁=1, x₂=2.

2.4. Wielomian interpolacyjny Hermite'a

Zagadnienie interpolacyjne Hermite'a jest uogólnieniem zagadnień interpolacyjnych Taylora i Lagrange'a. Wykorzystuje ono wartości funkcji oraz jej kolejnych pochodnych w różnych punktach. Inaczej mówiąc, wymagana jest w nim równość wartości funkcji interpolowanej i interpolującej oraz równość określonej liczby kolejnych pochodnych w ustalonych punktach.

Odnosi się to wszystko zarówno do przypadku funkcji f i węzłów interpolacyjnych zespolonych, w szczególnym przypadku rzeczywistych.

Zadanie interpolacyjne Hermite'a ma jednoznaczne rozwiązanie.

Nie podajemy ogólnego wzoru Hermite'a dla n-tego stopnia wielomianu z powodu dużego stopnia komplikacji wyprowadzenia i postaci. Można znależć go w [2] str. 279.

Dla przykładu podaję wzór interpolacyjny Hermite'a dla 3 stopnia wielomianu:

przykład

Znaleźć wzór interpolacyjny Hermite'a dla funkcji przy danych węzłach x₀=1 i x₁=2.

f(x₀)=1 f(x₁)=0,5

ω₃(x)=(x-1)⋅(x-2)

Stąd otrzymany wzór interpolacyjny Hermite'a ma postać:

H₃(x)=x³-1,75⋅x²+6,5⋅x-5,75

2.5. Wzory interpolacyjne Newtona

Wzory interpolacyjne Newtona są stosowane do rozwiązywania tego samego zagadnienia interpolacyjnego co i wzór Lagrange'a.

Wzór Lagrange'a jest niewygodny w przypadku gdy zmieniamy liczbę węzłów. Wtedy do wyznaczenia wielomianu określonego stopnia trzeba powtarzać od początku obliczenia. Innymi słowy, poprzez dodanie nowych węzłów nie daje się modyfikować wcześniej wyznaczonego wielomianu Lagrange'a.

Równoważny wielomianowi Lagrange'a, wielomian Newtona, usuwa tę niedogodność wzoru Lagrange'a. Wielomian ten posiada tę własność, że rozszerzenie zadania interpolacji o dodatkowy węzeł sprowadza się do obliczenia i dołączenia do poprzednio wyznaczonego wielomianu dodatkowego składnika.

2.4.1. Wzór interpolacyjny Newtona dla nierównych odstępów argumentu

Przyjmijmy, że funkcja f(x) jest określona za pomocą tablicy, x₀, x₁, ..., x_n, są węzłami interpolacji, a f(x₀), f(x₁), ..., f(x_n) odpowiadającymi tym węzłom wartościom funkcji f(x). Ponadto x_i≠x_j dla i≠j (i, j=0, 1, ..., n) i ponadto różnice

Δx_i=x_i+1-x_i i=0, 1, ...

nie są na ogół stałe.

Definiujemy wyrażenia zwane ilorazami różnicowymi:

- pierwszego rzędu

- drugiego rzędu (analogicznie)

- n-tego rzędu

dla n=1, 2, ... oraz i=0, 1, 2, ...

Z ilorazów różnicowych tworzy się zazwyczaj tablicę jak niżej:

xi	f(xi)	rzędu 1	rzędu 2	rzędu 3	rzędu 4	rzędu 5
x0 x1 x2 x3 x4 x5	f(x0) f(x1) f(x2) f(x3) f(x4) f(x5)	f(x0;x1) f(x1;x2) f(x2;x3) f(x3;x4) f(x4;x5)	f(x0;x1;x2) f(x1;x2;x3) f(x2;x3;x4) f(x3;x4;x5)	f(x0;x1;x2;x3) f(x1;x2;x3;x4) f(x2;x3;x4;x5)	f(x0;x1;x2;x3x4) f(x1;x2;x3;x4;x5)	f(x0;x1;x2;x3x4;x5)

Wykorzystując wzór interpolacyjny Lagrange'a po przekształceniach, które można znaleźć w [1] str. 41-43, można podać wzór na iloraz różnicowy w postaci:

Stąd można podać wzór interpolacyjny Newtona dla nierównych odstępów argumentów (wzór Newtona z ilorazami różnicowymi) dla ω_k(x)=(x-x₀)⋅(x-x₁)⋅. . .⋅(x-x_k):

(8)

2.4.2. Wzór interpolacyjny Newtona dla równoodległych wartości argumentu

Niech będą dane wartości funkcji f(x):

y_i=f(x_i) i=0, 1, ..., n

przy czym punkty x_i są rozmieszczone w jednakowych odstępach

x_i=x₀+i⋅h i=0, 1, ..., n h=const.

W przypadku węzłów równoodległych ilorazy różnicowe kolejnych rzędów wynoszą odpowiednio:

f(x₀)=a₀=y₀

Inaczej można to przedstawić jako:

przy czym 0!=1, Δ⁰y₀=y₀ i gdzie

Δy_k - to różnice skończone progresywne określone wzorami:

Podstawiając wyznaczone wartości współczynników a_k do wzoru (8) otrzymujemy

(9)

Jest to pierwszy wzór interpolacyjny Newtona, wielomian stopnia nie większego niż n.

W praktycznych zastosowaniach znacznie łatwiej jest stosować ten wielomian wprowadzając nową zmienną:

Ponieważ

więc wzór (9) ma postać:

Wielkość określa liczbę kroków potrzebnych do przejścia od punktu x₀ do punktu x.

Dla:

- n=1 otrzymujemy wzór na interpolację liniową:

- n=2 otrzymujemy wzór na interpolację paraboliczną:

przykład

Funkcja f(x)=e^x dana jest w przedziale <3,5;3,8> za pomocą tablicy wartości:

x	3,5	3,55	3,6	3,65	3,7	3,75	3,8
y	33,115	34,813	36,598	38,475	40,447	42,521	44,701

Obliczyć wartość funkcji w punkcie x=3,58.

W celu znalezienia wartości funkcji w punkcie x=3,58 budujemy wielomian interpolacyjny dla tej funkcji. Ponieważ x∈<3,55;3,60> jako x₀ należy przyjąć 3,55.

Tworzymy tablicę różnic:

x	y	Δy	Δ^2y	Δ^3y	Δ^4y	Δ^5y	Δ^6y
3,50 3,55 3,60 3,65 3,70 3,75 3,80	33,115 34,813 36,598 38,475 40,477 42,521 44,701	1,698 1,785 1,877 1,972 2,074 2,180	0,087 0,092 0,095 0,102 0,106	0,005 0,003 0,007 0,004	-0,002 0,004 -0,003	0,006 -0,007	-0,013

x₀=3,55 y₀=34,813 Δy₀=1,785 h=0,05

Dla x=3,58 i q=20⋅0,03=0,6 szukana wartość funkcji wynosi

f(3,58)=35,865794

III. Podsumowanie

Zastosowanie

Ogólnie interpolację stosuje się w następujących przypadkach:

• przy obliczaniu wartości funkcji określonej za pomocą tablicy wartości w punkcie różnym od podanych w tej tablicy,

• przy zagęszczaniu tablic,

• przy obliczaniu poprawek , na przykład dla stablicowanych funkcji o rzadkim kroku,

• przy zastępowaniu funkcji zbyt skomplikowanych wielomianem odpowiedniego stopnia.

Dokładność

Ważną sprawą jest dokładność z jaką wielomian interpolacyjny przybliża funkcję f(x) w punktach nie będących węzłami leżącymi wewnątrz przedziału <a;b> czyli określenie maksymalnego błędu bezwzględnego popełnionego przy interpolacji:

Jedynym czynnikiem, na który mamy wpływ i od którego zależy dokładność oszacowania wzoru interpolacyjnego jest czynnik:

ω_n(x)=(x-x₀)⋅(x-x₁)⋅. . .⋅(x-x_n)

Generalnie można powiedzieć, że aby zminimalizować błąd należy się starać, aby węzły były rozłożone po obu stronach danego punktu x, i to w miarę symetrycznie.

Zwiększanie liczby węzłów

Powstaje pytanie, czy przybliżenie polepszy się gdy zwiększy się liczbę węzłów. Okazuje się, że nie zawsze przy zwiększeniu liczby zmierzonych wartości funkcji można dokładniej opisać matematycznie tę zależność funkcyjną.

Takie zachowanie się wielomianu interpolującego (zwłaszcza przy końcach przedziału interpolacji) jest zjawiskiem typowym dla interpolacji za pomocą wielomianów wysokich stopni przy stałych odległościach węzłów - jest to tzw. zjawisko Rungego. Interpolacja tego typu na środkowych częściach przedziału <a;b> jest natomiast bardzo dobra.

Wybór stopnia wielomianu

Przy obliczeniach na maszynach cyfrowych problem wyboru stopnia wielomianu interpolacyjnego rozwiązuje się najczęściej tak, że gdy funkcja interpolowana dana jest za pomocą tablicy wartości, interpolację rozpoczynamy od n=1 (interpolacja liniowa) i zwiększając stopniowo liczbę węzłów zwiększamy stopień wielomianu aż do ustabilizowania się istotnych dla nas miejsc dziesiętnych pamiętając o istnieniu maksymalnej granicznej dokładności, której na ogół nie można przekroczyć.

Bibliografia

Z. Fortuna, B. Macukow, J. Wąsowski „Metody numeryczne”, WNT Warszawa 1993

Wanda Ronka-Chmielowiec, Antoni Smoluk „Metody numeryczne”, skrypt AE we Wrocławiu, 1978

Janina i Michał Jankowscy „Przegląd metod i algorytmów numerycznych” cz. I, WNT 1981

Anthony Ralston „Wstęp do analizy numerycznej”, PWN Warszawa 1971

---