1. Wydajność pracy w pewnym zakładzie jest zmienna losową o rozkładzie normalnym X~N(12; 2). Wyznaczyć następujące prawdopodobieństwa:

1. że wydajność jest mniejsza od 15 ton/godz

2. że wydajność jest mniejsza od 7 ton/godz

3. że wydajność jest zawarta w przedziale od 8 do 16 ton/godz

4. że wydajność jest zawarta w przedziale od 8 do 13 ton/godz

5. że wydajność przekroczy 19 ton/godz.

2. Na wspólnym układzie współrzędnych naszkicować gęstości rozkładów:

a) N(2; 2) N(2; 4) N(2;0,5)

b) N(2; 2) N(4; 2) N(0,5; 2)

3. Dystrybuanta zmiennej losowej X przedstawia się następująco:

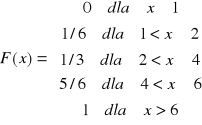
a) Wyznaczyć funkcje prawdopodobieństwa tej zmiennej.

b) Wyznaczyć: P(4≤X≤5); P(X>5); P(X≥5).

4. Wartość oczekiwana i odchylenie standardowe zmiennej losowej X o rozkładzie normalnym są odpowiednio równe 15 i 5. Znaleźć prawdopodobieństwo, że X przyjmie wartość:

1. mniejszą niż 12

2. większą niż 14

3. należącą do przedziału 12-14

5. Rozkład miesięcznych dochodów na 1 osobę w rodzinach pracowniczych trzyosobowych jest normalny o parametrach N(580 zł; 100 zł). Obliczyć:

1. prawdopodobieństwo, że w losowo wybranej rodzinie miesięczny dochód na 1 osobę będzie powyżej 800 zł

2. ile rodzin, spośród 1000 wybranych losowo, będzie miało miesięczny dochód na 1 osobę poniżej 600 zł.

6. Opóźnienie przyjazdu pewnego pociągu do stacji jest zmienna losową o rozkładzie normalnym N(15 min; 13 min). Obliczyć prawdopodobieństwo, że:

a) pociąg, który miał przyjechać o 22.00 przyjedzie między godz. 22.05 a 22.10;

b) ten sam pociąg przyjedzie po godz. 22.20.

Lista zadań nr 4 STATYSTYKA

---