Wydział: Inżynieria Lądowa	Dzień/godzina poniedziałek 11:15				NR zespołu: 24
		Data:		14.12.2009
1. Basaj Radosław 2. Filipek Dawid 3. Horbowicz Marcin		Ocena z przygotowania		Ocena z sprawozdania	Ocena końcowa
Prowadzący: dr Elżbieta Auguściuk				Podpis Prowadzącego:

1.TEMAT:

Drgania proste harmoniczne: wahadło rewersyjne i wahadło torsyjne.

2. CEL ĆWICZENIA:

Celem wykonywanego przez nas ćwiczenia było wyznaczenie przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego, oraz modułu sprężystości za pomocą wahadła torsyjnego.

3. WSTĘP TEORETYCZNY:

• wahadło rewersyjne

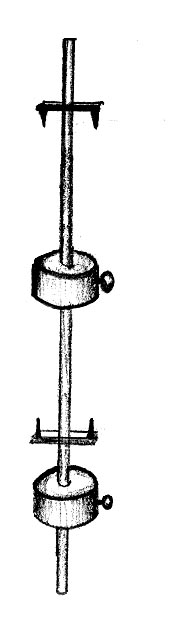
Jest to wahadło fizyczne wynalezione przez Henry'ego Katera (1777-1835) . Służy ono do wyznaczania przyspieszenia ziemskiego. Składa się z metalowego pręta z dwoma uchwytami na osie (najczęściej w postaci pryzmatów wykonanych z twardego materiału ) oraz z ruchomych ciężarków. Ciężarki ustawia się tak aby okres wahań wahadła względem jednej i drugiej osi był taki sam. Wtedy można też wyznaczyć przyspieszenie ziemskie na podstawie wzoru na wahadło matematyczne. W prosty sposób można udowodnić, że okres wahań wahadła rewersyjnego i matematycznego są wtedy opisane takimi samymi wzorami (z jedną drobną różnicą, że L we wzorze na wahadło rewersyjne oznacza tzw. długość zredukowaną). Długość zredukowana wahadła rewersyjnego jest to taka długość wahadła matematycznego, dla której okres wahań wahadła matematycznego i rewersyjnego są sobie równe.

stąd :

gdzie L- długość zredukowana wahadła

W naszym przypadku długością zredukowaną wahadła rewersyjnego będzie odległość między jego osiami.

• wahadło torsyjne

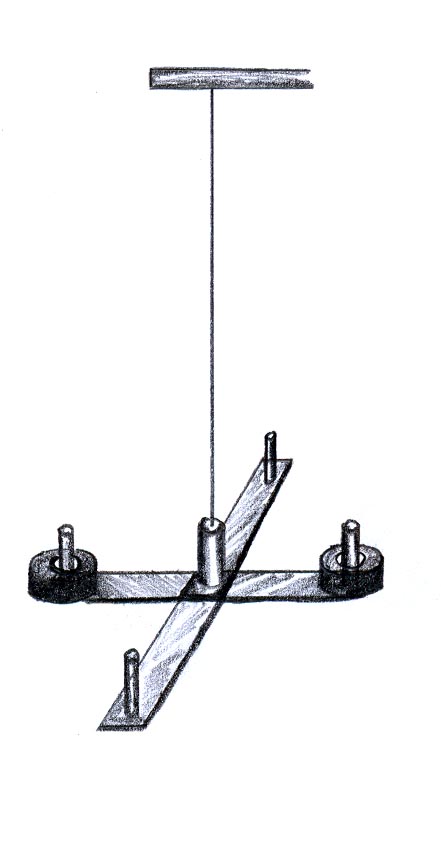
Wahadło torsujne składa się z czterech ramion, na których znajdują się ciężarki oraz metalowego pręta na którym wisi cała konstrukcja. W wahadle torsyjnym ruch spowodowany jest siłą skręcającą. Aby dokonać pomiaru długości okresu takiego wahadła należy wprawić wahadło w ruch skręcając pręt, a następnie zmierzyć około dwudziestu okresów (czyli czterdziestu przejść wahadła przez maksymalne wychylenia).

Wzór określający okres drgań wahadła torsyjnego jest analogiczny do równania opisującego ruch wahadła matematycznego, co nie znaczy identyczny.

D -współczynnik proporcjonalności:

gdzie G- moduł sprężystości, który należy wyznaczyć

Podstawiając powyższą równość do równania na okres drgań otrzymujemy:

Stąd możemy wyznaczyć moduł sprężystości G:

gdzie L- długość pręta, r -promień pręta

Wszystkie wielkości występujące w tym wzorze poza momentem bezwładności I możemy łatwo zmierzyć. Trudność tę omijamy mierząc okres drgań układu z różnym obciążeniem:

I_z - moment bezwładności dodatkowych ciężarków

Uwzględniając wzór na współczynnik proporcjonalności otrzymamy:

Skąd:

Zgodnie z twierdzeniem Steinera dla obciążenia w postaci jednorodnych walców wielkość:

n - ilość obciążników, m - masa walca, R - promień walca,

d - średnia odległość środka walca od osi układu

Po podstawieniu moduł sprężystości wyznaczamy ze wzoru:

OPIS WYKONANIA DOŚWIADCZENIA

Wahadło torsyjne (wyznaczanie modułu sprężystości):

1. Pomiar średnicy i długości badanego pręta:

L.p.	Średnica pręta [mm]
1	2,9±0,1
2	2,8±0,1
3	2,9±0,1
4	2,8±0,1
5	2,9±0,1
6	2,9±0,1
7	2,8±0,1
8	2,9±0,1
9	2,9±0,1
10	2,9±0,1

Wartość średnia średnicy pręta 2r = 2,87mm = 0,00287±0,0001 [m]

2. Pomiar długości badanego pręta:

Długość pręta L= 1,024±0,001 [m]

3. Pomiar czasu 20 drgnień wibratora nieobciążonego:

t₁ = 26,83 ±0,2 [s] - czas 20 wahnięć

T₁ = 1,34±0,01 [s] - okres

4. Pomiar średnicy n dodatkowych ciężarków:

Średnica ciężarka 2R= 0,086±0,0001 [m]

5. Pomiar masy n dodatkowych ciężarków:

Waga ciężarka = 580,5 [g] = 0,5805 ± 0,001 [kg]

6. Pomiar odległości między sztyftami na których umieszczone zostaną ciężarki:

Odległość między sztyftami 2d= 26,0 [cm] = 0,26±0,001 [m]

7. Pomiar czasu 20 drgnień wibratora obciążonego przez 4 ciężarki:

t₂ = 60,11±0,2 [s]- czas 20 wahnięć

T₂ = 3,01±0,01 [s] - okres

8. Wyznaczenie wielkości G:

Odległość sztyftów od osi :

d=0,13±0,001 [m]

Długość pręta L= 1,024±0,001 [m]

Promień badanego pręta :

r=0,001435±0,00005 [m]

Okres drgań wahadła bez obciążników :

T₁ = 1,34±0,01 [s]

Okres drgań wahadła z obciążnikami :

T₂ = 3,01±0,01 [s]

Promień ciężarka : R= 0,043±0,0001 [m]

Ilość ciężarków :

n=4

Waga ciężarka m= 0,5805 ± 0,001 [kg]

Wartość G policzono według wzoru:




G = 5.956674*10¹⁰N/m²

9. Błąd liczymy metodą różniczki zupełnej:




Otrzymaliśmy wartość G=5,96±0,07*10¹⁰ [N/m²]

Wniosek:

Wartość G dla stali wynosi 8,5*10¹⁰, więc wynik odbiega nieco od wartości tablicowej.

1.Wahadło rewersyjne (wyznaczanie przyspieszenia ziemskiego):

1. Ustawiono ciężarek m_B w odległości równej połowie odległości między osiami

2. Ustawiono ciężarek m_A jak najbliżej osi O`

3. Pomierzono długości 20 okresów drgań wahadła względem jednej i drugiej osi.

4. Następnie dokonano kolejnych pomiarów każdorazowo zwiększając odległość ciężarka m_A od osi O` o 3cm.

Wyniki:

Przesunięcie ciężarka mA [cm]	Czas 20 wahnięć względem osi O - t[sek]	Okres drgań wahadła względem osi O - T[sek]	Czas 20 wahnięć względem osi O' - t'[sek]	Okres drgań wahadła względem osi O' - T'[sek]
4	33,35±0,2	1,76±0,01	33,94±0,2	1,70±0,01
7	35,55±0,2	1,78±0,01	34,57±0,2	1,73±0,01
10	35,93±0,2	1,80±0,01	35,57±0,2	1,78±0,01
13	36,30±0,2	1,81±0,01	36,49±0,2	1,82±0,01
16	36,66±0,2	1,83±0,01	37,33±0,2	1,87±0,01
19	36,94±0,2	1,85±0,01	38,46±0,2	1,92±0,01
22	37,27±0,2	1,86±0,01	39,57±0,2	1,98±0,01
25	37,78±0,2	1,89±0,01	40,83±0,2	2,04±0,01
28	37,95±0,2	1,90±0,01	42,24±0,2	2,11±0,01
31	38,29±0,2	1,91±0,01	44,08±0,2	2,20±0,01
34	38,68±0,2	1,93±0,01	45,76±0,2	2,29±0,01




Wykresy przecięły się dla wartości 12 cm. Zgodnie z instrukcją pomiar powtórzono przy odległości ciężarka m_A od osi O' równej 12cm i otrzymano podobne wyniki:

mieszczące się w granicach błędu: t=36,17±0,2 oraz t'=36,11±0,2. Zatem:

T=1,81±0,01 [s]

Długość zredukowana L=80,5±0,1 [cm]

Wartość przyspieszenia została wyliczona ze wzoru:




g=9,73 ±0.23 m/s²

Błąd g został wyznaczony metodą różniczki zupełnej:




Wyznaczona wartość przyspieszenia ziemskiego równa jest g=9,73 m/s² ± 0,23 natomiast wartość tablicowa to g=9,81 m/s². W związku z czym metoda ta jest skuteczna, gdyż wartość wyznaczona różni się nieznacznie od wartości tablicowej.

---