WSTĘP TEORETYCZNY

Kinetyka zajmuje się zmiennością w czasie reagujących ze sobą układów chemicznych. Badania kinetyczne dostarczają informacji o przebiegu reakcji chemicznych oraz stanowią podstawę projektowania reaktorów.

Wyniki pomiarów kinetycznych opisujemy równaniami , które w większości przypadków wyrażają zależność szybkości reakcji r od stężeń reagentów i od temperatury. Jeśli chcemy znać nie tylko postać równań kinetycznych , lecz zrozumieć również ich powiązanie z molekularnym przebiegiem reakcji , musimy poznać mechanizm reakcji.

Szybkość reakcji chemicznej r w układzie reakcyjnym o stałej objętości definiujemy jako zmianę stężenia c reagenta w czasie t :

(1)

Równanie kinetyczne jest zależnością czysto empiryczną , którą można się bezpiecznie posługiwać tylko w warunkach , dla których została wyznaczona.

Stała szybkości reakcji zależy wykładniczo od temperatury (równanie Arrheniusa) :

(2)

gdzie R jest stałą gazową , E energią aktywacji , a A - czynnikiem przedwykładniczym.

Równanie Arrheniusa jest równaniem wykładniczym , co wskazuje na znaczny wpływ temperatury na szybkość reakcji chemicznej. Im większa jest energia aktywacji tym większy jest ten wpływ. Logarytmując równanie Arrheniusa otrzymujemy

(3)

W celu wyznaczenia stałych E i A bada się szybkość reakcji w różnych temperaturach , a znalezione stałe szybkości reakcji k przedstawia się na wykresie w układzie współrzędnych : ln k - odwrotność temperatury bezwzględnej.

Kąt skręcenia α substancji optycznie czynnej w danej temperaturze i dla danej długości światła zależy od długości d drogi światła i od stężenia c danej substancji

α = β dc (4)

gdzie β - skręcalność właściwa.

Oznaczając przez α₀ wartość kąta skręcenia w momencie początkowym ( po czasie t₁ ) , przez α w danym momencie czasu t_i , a przez α_∞ - po zakończeniu reakcji ( t = ∞ ) , można równanie

(5)

przedstawić w postaci

(6)

Różnica kątów skręcenia (α₀ - α_∞) jest bowiem proporcjonalna do początkowego stężenia c₀ substratu , a (α - α_∞) do stężenia aktualnego c.

Równanie [6] można przekształcić do postaci

ln (α₀ - α_∞) - ln (α - α_∞) = k₀t

- ln (α - α_∞) = - ln (α₀ - α_∞) + k₀t (7)

co daje równanie prostej o współczynniku kierunkowym k₀ i rzędnej przecięcia z osią y równej ln (α₀ - α_∞).

Reakcja inwersji sacharozy jest przykładem reakcji katalizowanej przez kwas.

OPRACOWANIE WYNIKÓW

1. Wyniki zestawiono w tabeli :

Nr pomiaru	Czas [min]	Kąt skręc.  [^0]	-∞	y=-ln(∞)	t^2	yt
1.	5	8,2	11,6	-2,451	25	-12,255
2.	10	7	10,4	-2,342	100	-23,418
3.	15	5,5	8,9	-2,186	225	-32,791
4.	20	4,4	7,8	-2,054	400	-41,082
5.	25	3,5	6,9	-1,932	625	-48,288
6.	30	2,6	6	-1,792	900	-53,753
7.	40	0,9	4,3	-1,459	1600	-58,345
8.	50	-0,35	3,05	-1,115	2500	-55,757
9.	60	-1,2	2,2	-0,788	3600	-47,307
10.	nieskon	-3,4
suma	255	-	-	-16,118	9975	-372,996
(suma t)^2	65025

liczba pomiarów n = 10

2. Wykreślenie zależności - ln (α - α_∞) = f(t)

3. Na podstawie równania prostej umieszczonego na wykresie odczytuję stałą szybkości reakcji katalizowanej przez kwas k , wiedząc , że jest ona równa współczynnikowi nachylenia prostej :

k = 0,0304

4. Stała szybkości reakcji k obliczona metodą najmniejszych kwadratów wynosi :

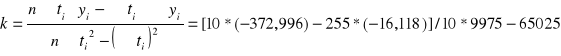
k = 0,011

Stała szybkości reakcji k różni się od wyniku uzyskanego w punkcie 3.

5. Skręcalność roztworu α₀ w momencie zmieszania roztworów ( t = 0 ) można obliczyć dwoma metodami korzystając z zależności:

a = - ln(α₀ - α_∞)

α₀ = exp(-a) +α_∞

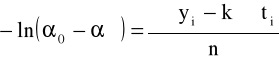
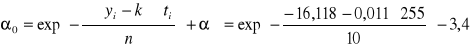
α₀ = -5,292

6. Czas po którym przereaguje połowa substratów wynosi :

minut.

Zakład Chemii Fizycznej

Laboratorium Studenckie

Ćwiczenie nr 20

SACHARYMETRIA. Wyznaczanie stałej szybkości inwersji cukru.

Tomasz Dziadosz

Lukasz Daniel

Inżynieria Chemiczna

rok II grupa I

1

---