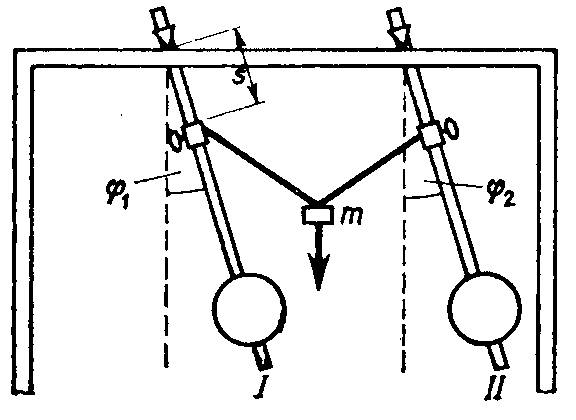
tyw na którym zawieszone są obydwa wahadła lub bezpośrednio przez sprężynę albo poprzez obciążoną w środku nić. Pierwszy rodzaj sprzężenia dla wahadeł zawieszonych na sztywnych statywach jest bardzo słaby, stąd w doświadczeniu stosuje sprzężenie bezpośrednie. Moment kierujący każdego z wahadeł, zgodnie z wzorem wynosi

D = mgl

gdzie m oznacza masę wahadła, l- odległość środka ciężkości od osi obrotu. Ponadto w przypadku wahadeł sprzężonych występuje moment sprzęgający D_s. Wartość tego momentu zależy od odległości s punktu zaczepienia siły sprzęgającej, od osi obrotu oraz od różnicy faz obydwu wahadeł

D_s = D_s(s, ϕ₁-ϕ₂)

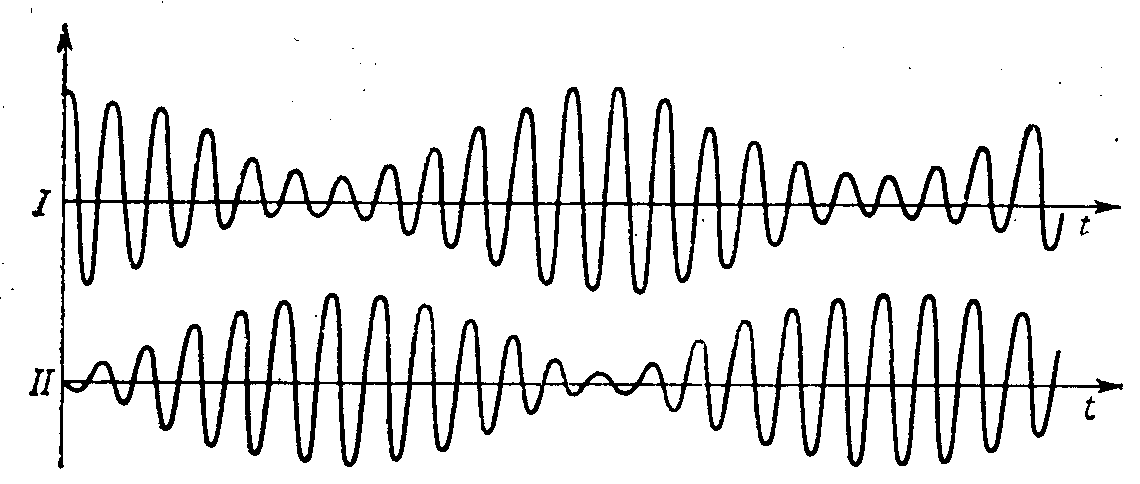
W przypadku wahadeł sprzężonych, których okresy drgań własnych są bardzo zbliżone, występują tzw. dudnienia o następującym przebiegu. Załóżmy, że w chwili początkowej wahadło II jest nieruchome, natomiast wahadło I wykonuje drgania.

Wtedy wahadło II (nieruchome) zacznie drgać i jego amplituda stale rośnie, natomiast amplituda drgań wahadła I maleje. Amplituda drgań wahadła II rośnie do chwili, gdy amplituda wahadła I zmaleje do zera. Następnie drgania przekazywane są znowu do wahadła I.

Czas, po którym amplituda drgań jednego z wahadeł wraca do początkowej wartości, nazywamy okresem dudnień T_d, a odpowiadającą mu częstość w_d - częstością dudnień. Przekazywania drgań nie obserwuje się, jeżeli wahadła wy­konują tzw. drgania normalne. W przypadku pierwszego drgania normalnego obydwa wahadła drgają w zgodnej fazie (Ifil.= lfi2) i nie działa moment sprzęgający, bowiem Ifi 1 -Ifi2 = o; drganie to zachodzi z częstością kołową w 1 zwaną .pierwszą częstością normalną i odpowiadającym jej okresem T 1. Dla drugiego drgania normalnego lfil = = -Ifi2 wprowadza się drugą częstość normalną w2 i okres T2. \

Równanie ruchu każdego z wahadeł musi być uzupełnione składnikiem określającym wpływ momentu sprzęgającego, stąd przyjmują one postać:

Uwzględniając podstawienia:

otrzymamy:

Uwzględniając powyższe podstawienia równania ruchu przyjmą postać:

Oznaczając przez C wychylenie dla t = 0, otrzymamy następujące rozwiązania tych równań:

co zgodnie z podstawieniami:

daje następujące wyrażenie na ϕ ϕ :

w wyrażeniach powyższych wielkości:

możemy uważać za powoli zmieniające się w czasie amplitudy. Tak więc równania (10.54) dają ściśle matematyczny opis krzywych z rysunku 10.14. Amplituda po czasie .T4 wrócić musi do pierwotnej wartości, czyli zgodnie z ostatnimi wyrażeniami otrzymamy

Interesujący jest przypadek, gdy częstości drgań składowych niewiele się różnią od siebie. Przyjmijmy dla uproszczenia, że amplitudy dwu drgań skła­dowych są jednakowe i równe a, pulsacje zaś - odpowiednio równe ω_l i ω₂ przyjmujemy ponadto, że w chwili t = 0 fazy obu drgań są jednakowe i równe zeru. Mamy wówczas:

Jeśli

możemy z wystarczającym przybliżeniem uważać ruch wypadkowy za drganie harmoniczne proste o pulsacji (ω_l + ω₂)/2 i amplitudzie zależnej od czasu, a mianowicie drgającej harmonicznie z pulsacją ∆ω/2 i z amplitudą 2a. Amplituda wypadkowego drgania zmienia się zatem od zera do maksymalnej wartości 2a. Tego typu zmianę amplitudy nazywamy dudnieniem; okres dudnie­nia jest to czas od osiągnięcia przezeń maksymalnej amplitudy do osiągnięcia następnego maximum amplitudy. Odpowiada to zmianie argumentu wyraże­nia cos[(ω_l - ω₂)t/2] od wartości n_π do wartości (n+l)π, gdzie n jest liczbą całkowitą. Zmiana ta zachodzi w czasie T_d; mamy zatem

skąd

Dudnienia odgrywają dużą rolę w akustyce. Również i w przypadku, gdy amplitudy dwu drgań składowych są niejednakowe, drganie wypadkowe ma charakter dudnienia. Na rys. widzimy przykład dudnienia.

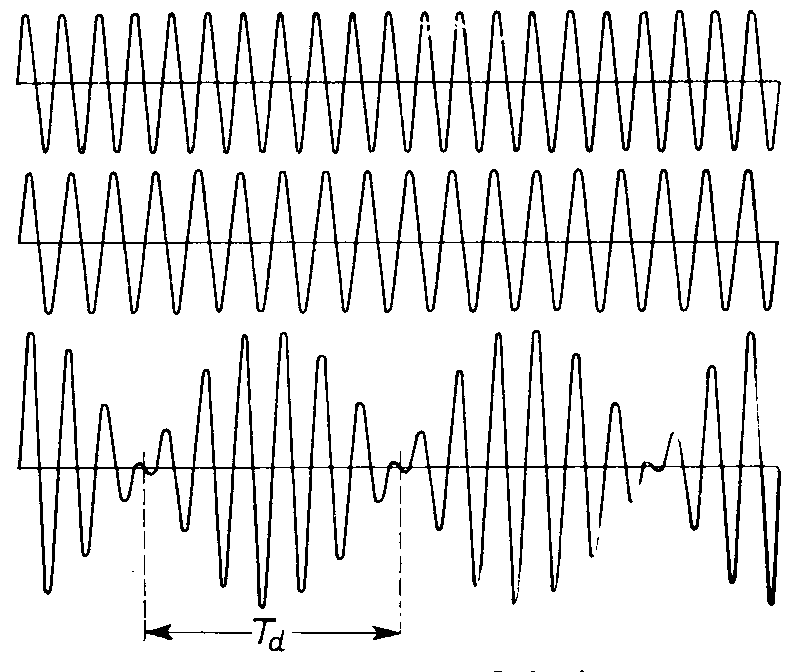
Rys. Dudnienia

Doświadczalnie można zademonstrować nakładanie się na siebie dwu drgań harmonicznych w jednym kierunku za pomocą urządzenia pokazanego schema­tycznie na rys. VIII.ll. Widzimy tu dwie poziome taśmowe sprężyny, mogące, wykonywać drgania w kierunku pionowymi drgania te możemy z wystarczają­cym przybliżeniem uważać za harmoniczne. Pulsację drgań możemy zmieniać zmieniając długość taśm. Do każdej z taśm przymocowane jest zwierciadełko, biorące oczywiście udział w drganiach. Na zwierciadełka rzucamy smukłą wiązkę światła, która po odbiciu od nich pada na ekran. Na drodze dwu­krotnie odbitego promienia ustawiamy zwierciadło szybko wirujące, dzięki czemu drgania plamki świetlnej na ekranie rozciągnięte zostają w krzywą charakteryzującą przebieg drgania wypadkowego 'v czasie.

Oczywiście możemy składać ze sobą nie tylko dwa, lecz i dowolną liczbę drgań harmonicznych o różnych częstotliwościach. Jeśli stosunki tych częstotliwości są liczbami wymiernymi, wypadkowe drganie jest periodyczne. Od­wrotnie, dowolne drganie harmoniczne periodyczne rozłożyć można na drgania harmoniczne proste. Jak pokazał Fourier, każde drganie periodyczne:

x = f(t) ,

o okresie T, to znaczy takie, że

f(t+T) = f(t) ,

rozwinąć można na nieskończony zbieżny szereg drgań harmonicznych pro­stych, tak że:

f(t) = A₀+A₁cosωt+A₂cos2ωt+ ... +B_lsinωt+B₂sin2ωt+ , ... ,

przy czym

współczynniki zaś A_n i B_n są jednoznacznie określone. Oczywiście funkcja f(t) spełniać musi pewne, zresztą bardzo ogólne, warunki. Prócz pulsacji podstawowej ω w szeregu (45.12) występują całkowite wielokrotności tej pulsacji, tzw. pulsacje harmoniczne lub alikwoty. Alikwoty odgrywają dużą rolę w akustyce, o czym będzie mowa później. Niektóre ze współczynników A_n i B_n mogą być oczywiście równe zeru. Dla przykładu na rys. VIII.12 pokazana jest ana­liza fourierowska drgania trójkątnego. Mamy mianowicie dla tego drgania:

Na rys. VIII.12b uwzględniono wypisane cztery wyrazy szeregu Fouriera (45.14); drganie wynikające z nałożenia na siebie tych czterech drgań harmo­nicznych prostych widzimy na rys. VIII.12c.

Odmienne wyniki uzyskamy, jeśli drgania składowe odbywają się wzdłuż prostopadłych do siebie osi x i y. Drganie harmoniczne proste wprowadziliśmy w § 43 jako ruch rzutu punktu obiegającego koło ze stałą szybkością kątową ω na oś poziomą czy pionową (rys. VIII.1). W ten sposób wprowadziliśmy dwa drgania harmoniczne proste, określone równaniami:

x = acosωt

oraz

y = asinωt

Podnosząc oba równania do kwadratu i dodając do siebie otrzymamy

x²+y² = a²,

a więc istotnie równanie koła o promieniu a; x oraz y możemy interpretować jako współrzędne punktu na tym kole. Możliwa jest jednak i inna interpretacja: możemy uważać, że rozpatrywany przez nas punkt materialny wykonuje równocześnie dwa drgania o tej samej pulsacji ω wzdłuż prostopadłych do siebie osi - przy czym pomiędzy drganiami tymi występuje różnica fazy o kąt π/2, gdyż :

y = asinωt = acos(ωt - π/2) .

Drganie wzdłuż osi y opóźnione jest w fazie o π/2 względem drgania wzdłuż osi x. Ponieważ kąt fazo­wy 2π odpowiada pełnemu okresowi drgań, oznacza to, że drganie wzdłuż osi y opóźnione jest o ćwierć okresu względem drgania wzdłuż osi x.

W każdej chwili położenie punktu materialnego wykonującego drgania składowe określić można do­dając do siebie wektory reprezentujące na osiach x i y odpowiednie wychylenia. Z rys. VIII.13 łatwo się przekonać, że wypadkowy ruch jest istotnie obiegiem po kole ze stałą szybkością kątową ω w kie­runku przeciwnym ruchowi wskazówek zegara. Zobaczymy jeszcze, jak ruch wypadkowy zależy od różnicy faz drgań składowych. W tym celu przyjmijmy najpierw, że oba drgania składowe nie różnią się w fazie. Mamy wówczas

x = acosωt,

y= acosωt.

Z równań tych wynika, że

x = y.

Jest to równanie prostej, pochylonej pod kątem 45° względem osi x (rys. VIII.14). Drganie wypadkowe odbywa się wzdłuż tej prostej, a wychylenie maksymalne równe jest
.

Jeśli różnica faz drgań składowych wynosi -π, to mamy

x = acosωt,

y= acos(ωt-π) = -acosωt,

skąd wynika, że

x= -y.

W tym przypadku drganie wypadkowe odbywa się wzdłuż prostej pochylonej pod kątem -45° względem osi x (rys. VIII.15).

Gdy wreszcie zapóźnienie w fazie drgania pionowego wynosi -3π /2 mamy

x = acosωt,

y = acos(ωt-3/2 π) = acos (ωt+π/2) = - asinωt.

W tym przypadku mamy znów

x²+y² = a²,

a więc ruch odbywa się po kole. Łatwo się jednak przekonać, że o ile w przypadku zapóźnienia o π/2 ruch odbywał się w zwrocie przeciwnym zwrotowi ruchu wskazówek zegara, teraz odbywa się on zgodnie z obiegiem wskazówek (rys. VIII.16). Analogiczną sytuację znaleźlibyśmy, gdyby drganie w kie­runku osi y odpowiednio wyprzedzało w fazie drganie w kierunku osi x.

Jeśli będziemy pamiętać, że zmiana fazy o kąt 2π nie wpływa na sytuację, łatwo stwierdzić, że opóźnienie w fazie o π/2 drgania w kierunku osi y względem drgania w kierunku osi x oznacza dokładnie to samo, co wyprzedzenie w fazie drgania wzdłuż osi x przez drganie wzdłuż osi y o 3π /2, analogicznie przedstawia się sprawa dla innych opóźnień czy wyprzedzeń w fazie.

Jeśli zapóźnienie w fazie drgania w kierunku osi y względem drgań w kie­runku osi x ma dowolną wartość ϕ, mamy wówczas

x = acosωt,

y = acos(ωt-ϕ) = a(cosωtcosϕ+sinωtsinϕ).

Z wzorów tych znajdujemy

y-xcosϕ = asinωtsinϕ,

podnosząc zaś wzory (45.30) oraz wzór (45.28) pomnożony przez sinϕ do kwa­dratu i dodając do siebie otrzymamy

(y-xcosϕ)²+x²sin²ϕ= a²sin²ϕ

Jest to równanie krzywej stożkowej, która musi być elipsą, gdyż, jak widać z równań (45.28) i (45.29), wpisana jest ona w kwadrat o boku 2a (rys. VIII.17). Elipsa ta przechodzi w koło dla ϕ= π/2 lub 3π/2, a w prostą dla ϕ = 0 lub ϕ= π. Dla kątów 0 ≤ ϕ ≤ π elipsa obiegana jest przez punkt drgający w kie­runku przeciwnym ruchowi wskazówek zegara, dla kątów ϕ zaś większych od π - zgodnie z ruchem wskazówek zegara. Wielkie osie tych wszystkich elips pochylone są pod kątem π/ 4 bądź - π/4 do osi x.

Jeślii amplitudy drgań w kierunkach osi x i y są niejednakowe, równe odpowiednio a i b, mamy wówczas:

x = acosωt,

y = bcos(ωt-ϕ).

Postępując jak w przypadku poprzednim znajdujemy

a więc znów równanie elipsy, wpisanej tym razem w prostokąt o bokach 2a wzdh1ż osi x i 2b wzdh1ż osi y. (rys. VIII.18)j

Na rys. VIII.19a widzimy wyniki składania drgań (45.28) i (45.29), na rys. VIII.19b zaś składanie drgań (45.33) i (45.34) dla różnych wartości róż­nicy faz <p.

Dwa drgania harmoniczne o jednakowych amplitudach w kierunkach do siebie prostopadłych z różnicą faz 7t/2 lub -7t/2 składają się, jak wiemy, na drgania kołowe, przebiegane dla <p = - 7t/2 przeciwnie niż ruch wskazówek ~ zegara, a dla <p = 7t/2 zgodnie z ruchem wskazówek zegara. W pierwszym przy­padku mamy

x = acos wt ,

y = acos ( wt- ~) ,

w drugim zaś

x = acos wt ,

y = acos ( wt+ ~) .

Zobaczymy teraz, jaki wynik da nałożenie na siebie dwu tych drgań kołowych. Znajdziemy

x = 2acos wt ,

Y=O.

Jak widzimy, w wyniku nałożenia na siebie dwu przeciwsobnych drgań koło­wych otrzymamy drganie harmoniczne proste o tej samej pulsacji, lecz zdwojo­nej amplitudzie.

Jeśli częstotliwości nakładanych na siebie dwu drgań harmonicznych w kie­runkach wzajemnie do siebie prostopadłych nie są sobie równe, ale stosunek ich jest liczbą wymierną, w wyniku nakładania na siebie tych drgań uzyskujemy

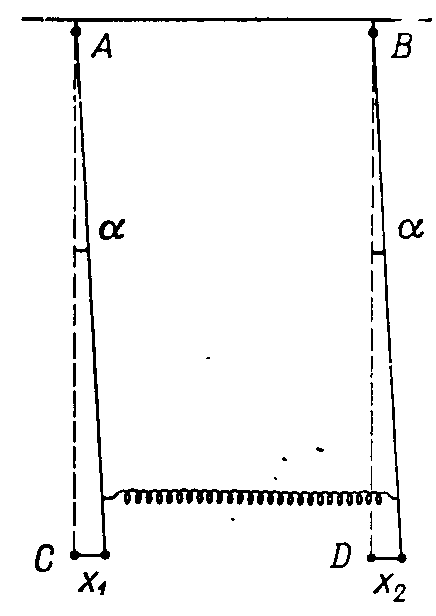
Rozpatrzmy jeszcze przypadek, gdy mamy do czynienia z dwoma pun­ktami materialnymi, wykonującymi drgania harmoniczne i oddziałującymi wzajemnie na siebie, Weźmy pod uwagę jako najprostszy przypadek tego rodzaju dwa jednakowej długości i o jednakowej masie wahadła, połączone ze sobą lekką sprężyną.

Oznaczmy wychylenie pierwszego z nich z położenia równowagi przez x₁, drugiego przez x₂. Równania ruchu wahadeł mają postać (zakładamy, że wychylenia są na tyle małe, że możemy uważać łuki zakreślone przez wychylające się kulki za odcinki prostej):

d2.'1!1 mg

mdi2 = - T .'1!1 + k(.'1!2- .'1!1) ,

d2.'1!2 mg

[mdt2 = - T .'1!2+ k(.'1!1-.'1!2) ;

przyjmujemy, że napięcie sprężyny proporcjonalne jest do jej rozciągnięcia. Jak wynika z powyższych równań, drgania wahadeł połączonych sprężyną przebiegają inaczej niż drgania wahadeł swobodnych; są one wzajemnie uzależ­nione, a ich okresy ulegają zmianie. Można wykazać, że każde z wahadeł wy­konuje drgania złożone z dwu drgań harmonicznych prostych o różnych częstotliwościach, przy czym w tych drganiach złożonych występują dudnienia. Istnieją jednak pewne przypadki, w których oba wahadła wykonują łącznie ruch drgający prosty. Pierwszy przypadek otrzymamy, gdy w chwili począt­kowej oba wahadła jednakowo wychylimy i puścimy swobodnie. Mamy wtedy w chwili t = 0

.'1!1(0) = .'1!2(0) ,

co oznacza, że w chwili początkowej wahadła podlegają tylko działaniu siły ciężkości; będą więc one drgać z jednakowymi częstotliwościami i warunek będzie stale spełniony. Wahadła będą zatem wykonywać drgania stale zgodne w fazie z częstotliwością taką samą, jak gdyby były swobodne. Mamy tu przykład drgania normalnego.

Drugie drganie normalne otrzymamy, gdy w chwili początkowej wahadła wychylimy o jednakowe kąty w kierunkach przeciwnych i puścimy swobodnie. W chwili t = 0 mamy zatem

.'1!1(0) = -.'1!~(0) .

Wahadła wykonują wahania ruchem przeciwsobnym i ruch ich będzie stale przeciwsobny. Możemy zatem położyć

.'1!1 = - .'1!2 .

oraz

Równania (45.39) i (45.40) przybierają postać:

d2.'1!1 mg mdt2= -T.'1!1-2k.'1!1' d2.'1!2 mg mdt2 = -T.'1!2-2k.'1!2 .

Postać obu równań jest identyczna, a mianowicie: d2.'1! (g 2k) dt2=-l+m.'1!.

Równanie powyższe opisuje drgania harmoniczne proste o pulsacji w:

x = Acoswt ,

przy czym mamy

w2 = !1 + ~

l m'

skąd

Jak widzimy, częstotliwość takich wahań przeciwsobnych, składających się na drgania normalne układu dwu wahadeł, jest wyższa niż częstotliwość wahań wahadła swobodnego czy też wahań zgodnych w fazie.

Analogiczną sytuację spotykamy w przypadku ogólnym, gdy mamy do czynienia z układem N punktów materialnych, oddziałujących wzajemnie na siebie siłami sprężystymi. W kursie mechaniki teoretycznej wykazuje się, że istnieje wówczas N drgań harmonicznych normalnych, to jest takich, że wszyst­kie punkty drgają równocześnie w pewien uzgodniony fazowo sposób.

Drgania normalne odgrywają dużą rolę w różnych działach fizyki, w szczególności, gdy chodzi o drgania sieci krystalicznej (fizyka ciała stałego), drgania wewnątrzcząsteczkowe (fizyka cząsteczek), akustykę, elektroakustykę.

---