Babelkowe:

void b_sort(int tablica[10], int ile_liczb)

{int temp,i,zmiana;

do

{

zmiana=0;

i=ile_liczb-1;

do

{

i--;

if (tablica[i+1]< tablica[i])

{

temp=tablica[i];

tablica[i]=tablica[i+1];

tablica[i+1]=temp;

zmiana=1;

}

}

while (i!=0);

}

while (zmiana!=0);

Szybkie:

void quicksort(int tablica[10], int x, int y)

{

int i,j,v,temp;

i=x;

j=y;

v=tablica[div(x+y,2).quot];

do

{

while (tablica[i]<v) i++;

while (v<tablica[j]) j--;

if (i<=j)

{

temp=tablica[i];

tablica[i]=tablica[j];

tablica[j]=temp;

i++;

j--;

}

}

while (i<=j);

if (x<j) quicksort(tablica,x,j);

if (i<y) quicksort(tablica,i,y);

}

Sortowanie przez wymianę/wybór (selectionsort)

void selectionsort(int tablica[10], int ile_liczb)

{

int min,i,j,temp;

for (i=0;i<ile_liczb-1;i++)

{

min=i;

for (j=i+1;j<ile_liczb;j++)

if (tablica[j]<tablica[min]) min=j;

temp=tablica[min];

tablica[min]=tablica[i];

tablica[i]=temp;

}

Cykl Eulera:

Cykl Eulera, to taki cykl w grafie, który zawiera każdą krawędź grafu dokładnie raz. Warunkiem istnienia cyklu są:

• spójność grafu,

• dla grafu skierowanego należy sprawdzić czy do każdego wierzchołka wchodzi tyle samo krawędzi co wychodzi

• dla grafu nieskierowanego z każdego wierzchołka musi wychodzić parzysta liczba krawędzi.

Szukanie cyklu:
Zaczynamy od dowolnego wierzchołka (w naszym przypadku będzie to ten z najmniejszym indeksem), dodajemy ten wierzchołek na stos i idziemy do następnego, osiągalnego z niego wierzchołka z najmniejszym indeksem, a łącząca go z nim drogę usuwamy (rys.1), dodajemy ten wierzchołek na stos i idziemy do następnego, osiągalnego wierzchołka z najmniejszym indeksem, a łączącą go z nim drogę usuwamy (rys.2), itd...
Jeżeli nie możemy już nigdzie pójść pobieramy element ze stosu (będzie on kolejnym w cyklu) i teraz z ostatniego wierzchołka na stosie idziemy dalej (rys. 4). Czynność powtarzamy tak długo jak długo mamy jakieś wierzchołki na stosie Oto przykłądowy graf

Przebieg algorytmu:

Stos: a,b Cykl:	Stos: a,b,c Cykl:
Stos: a,b,c,a Cykl:	Stos: a,b,d Cykl: a,c
Stos: a,b,d,e,b Cykl: a,c

Teraz już nigdzie nie możemy pójść więc zdejmujemy kolejno wierzchołki ze stosu i dodajemy je do cyklu. Końcowy wynik tych operacji to cykl: a,c,b,e,d,b,a.

Znajdowanie wypukłej otoczki (algorytm Grahama)

Wypukła otoczka zbioru punktów Q to najmniejszy wypukły wielokąt taki, że każdy punkt ze zbioru Q leży albo na brzegu wielokąta albo w jego wnętrzu.
Oto przykład:

Jak widać otoczka składa się z 6 wierzchołków, jest to najmniejszy podzbiór zbioru Q taki że ich ciąg tworzy otoczkę zbioru Q.
Przeanalizujemy teraz algorytm Grahama, zakładamy przy tym, że zbiór Q jest uporządkowany w następujący sposób:

1. wierzchołek o najmniejszym indeksie (u nas a) ma najmniejszą wartość y (jeśli jest kilka wierzchołków o najmniejszej wartości y, wybieramy skrajnie lewy)

2. kolejne wierzchołki (u nas b do j) są posortowane ze względu na kąt nachylenia ich wektorów wodzących do osi X

Takie uporządkowanie możemy otrzymać za pomocą algorytmu porządkowania wierzchołków.
Na poniższym rysunku widać proste zawierające wektory wodzące punktów, z kątów których wynika przyjęty porządek:

Punkt a ze względu na swe położenie jest oczywiście pierwszym wierzchołkiem otoczki. Algorytm Grahama polega na przechodzeniu do kolejnych wierzchołków z posortowanej listy, umieszczaniu ich na stosie i sprawdzaniu kierunku, w którym nastąpiło to przejście:

1. jeżeli odchylenie nastąpiło w prawą stronę, zdejmowany jest wierzchołek ze stosu

2. jeżeli odchylenie nastąpiło w stronę lewą, wierzchołek pozostaje na stosie

Oto algorytm zapisany w pseudokodzie:
Niech S₁ oznacza element na szczycie stosu a S₂ element pod nim
m- liczba punktów
p_i (i=0...m) oznacza i-ty punkt z uporządkowanej listy (w analogii do rysunku: p₀=a, p₁=b itd...) K oznacza kąt między punktami S₂, S₁ oraz p_i

1. Umieść na stosie punkty p₀, p₁ i p₂

2. for i=3 to m do {

3.   while K nie oznacza skrętu w lewo

4.       do Usuń punkt ze stosu

5.   Dodaj na stos punkt p_i

6. }

Jak widać kluczową czynnością w algorytmie jest określanie kierunku, w którym przechodzimy do następnego punktu. Można do tego celu wykorzystać metodę wyznaczników (opisaną w algorytmie współliniowości trzech punktów). Będziemy brać pod uwagę dwa wektory zaczepione we wspólnym punkcie.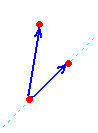


Np. zał. że na szczycie stosu mamy punkt b a tuż pod nim punkt a. Kolejnym punktem do przeanalizowania jest punkt c, chcemy sprawdzić, czy przechodząc do tego punktu (z punktu b) skręcimy w lewo, czy w prawo. Tworzymy więc dwa wektory AB oraz AC (zob. rysunek). Następnie za pomocą wyznaczników sprawdzamy po której stronie wektora AB leży punkt c. W przykładzie z rysunku wyznacznik det(a,b,c)>0 (gdyż punkt c leży po lewej stronie wektora). A zatem przechodząc z punktu b do punktu c skręcimy w lewo.




Przeanalizujemy teraz kilka kroków algorytmu, dany jest uporządkowany ciąg punktów:

Wykonujemy pierwszy punkt algorytmy S={a, b, c} (zawartość stosu na rysunku jest oznaczona jako ciąg wierzchołków wyznaczający łamaną) i inicjujemy zmienną i=3 (m=9):

sprawdzamy, po której stronie wektora BC znajduje się punkt wskazany przez zmienną i=3 (pamiętajmy, że liczymy od 0) a więc det(b,c,d). Z rysunku widać, że punkt ten leży po prawej stronie, więc obliczony wyznacznik będzie miał wartość ujemną. A zatem przechodząc przez ten punkt skręcimy w prawo. zgodnie z punktem 4. algorytmu usuwamy jeden punkt ze stosu: S={a,b}

Sprawdzamy więc, po której stronie wektora AB (gdyż C usunęliśmy) leży punkt d (zmienna i nadal ma wartość 3). Obliczymy, że det(a,b,d)>0, a więc skręcamy w lewo zatem dodajemy punkt d na stos i inkrementujemy zmienną (i++).

Zmienna i wskazuje na punkt e, na szczycie stosu mamy punkty d i b, zatem obliczamy det(b,d,e), otrzymujemy wartość ujemną, co oznacza skręt w prawo. Zdejmujemy więc wierzchołek ze stosu, czyli S={a, b}:

badamy det(a,b,e) i otrzymujemy wartość dodatnią, dodajemy wierzchołek e na stos (S={a,b,e}) i inkrementujemy zmienną i.

Algorytm Ameba:

Podstawowe operacje algorytmu Ameba:

- uporządkowanie

F(x0)>F(x1)>…>F(xn)

- odbicie

xr = x + (x - xn)

- F(xr)

a) F(xr)>F(x0) dokonujemy ekspansji

xs = xr + (x - xn)

F(xs)>F(xr)

xs xr

F(xs)<F(xr)

xr xs

b) F(xr)<F(xn-1) kontrakcja

xc = x + (x - xn)

xc xn

- skurczanie

xi = x0 + (xi - x0)

Złożoności obliczeniowe

F(n) = O(g(n)) pesymistyczny wariant złożoności obliczeniowej

0<f(n)<cg(n)

F(n) = (g(n)) optymistyczne ograniczenie od dolu

0<cg(n)<f(n)

F(n) = (g(n)) ograniczona z góry i z dołu jednocześnie

0<c1g(n)<f(n)<c2g(n)

F(n) = o(g(n)) dla dowolnych c>0

0<f(n)<cg(n))

F(n) = w(g(n)) dla dowolnych c>0

0<cg(n)<f(n)

Algorytm Kruskala

Algorytm polega na łączeniu wielu poddrzew w jedno za pomocą krawędzi o najmniejszej wadze. W rezultacie powstałe drzewo będzie minimalne. Na początek należy posortować wszystkie krawędzie w porządku niemalejącym. Po tej czynności można przystąpić do tworzenia drzewa. Proces ten nazywa się rozrastaniem lasu drzew. Wybieramy krawędzie o najmniejszej wadze i jeśli wybrana krawędź należy do dwóch różnych drzew należy je scalić (dodać do lasu). Krawędzie wybieramy tak długo, aż wszystkie wierzchołki nie będą należały do jednego drzewa.

Algorytm Prima

Budowę minimalnego drzewa rozpinającego zaczynamy od dowolnego wierzchołka, np. od pierwszego. Dodajemy wierzchołek do drzewa a wszystkie krawędzie incydentne umieszczamy na posortowanej wg. wag liście. Następnie zdejmujemy z listy pierwszą krawędź (o najmniejszej wadze). Sprawdzamy, czy drugi wierzchołek tej krawędzi nalerzy do tworzonego drzewa. Jeżeli tak, to nie ma sensu dodawać takiej krawędzi (bo oba jej wierzchołki znajdują sięw drzewie), porzucamy krawędź i pobieramy z listy następną. Jeżeli jednak wierzchołka nie ma w drzewie, to nalerzy dodać krawędź do drzewa, by wierzchołek ten znalazł się w drzewie rozpinającym. Następnie dodajemy do posortowanej listy wszystkie krawędzie incydentne z dodanym wierzchołkiem i pobieramy z niej kolejny element.
Jednym zdaniem: zawsze dodajemy do drzewa krawędź o najmniejszej wadze, osiągalną (w przeciwieństwie do Kruskala) z jakiegoś wierzchołka tego drzewa.

Przeszukiwanie grafu wszerz (BFS) i w głąb (DFS)

Procedury przeglądania grafu w głąb (DFS) i wszerz (BFS) są bardzo często wykorzystywane w innych, bardziej złożonych algorytmach (np. badania spójności).
W strategii DFS wybrany wierzchołek należy umieścić na stosie, zaznaczyć jako odwiedzony a następnie przejść do jego następnika. Następnik również umieszczamy na stosie, zaznaczamy jako odwiedzony przechodzimy do jego następnika. Jak widać procedurę można wywoływać rekurencyjnie. Jeśli dojdziemy do takiego wierzchołka, że nie ma on krawędzi incydentych z nieodwiedzonymi wierzchołkami, należy usunąć go ze stosu i pobrać ze stosu kolejny wierzchołek do przeszukania. W praktyce stosuje się zasadę, że jeśli przeszukiwany wierzchołek jest połączony krawędziami z wieloma wierzchołkami, wybiera się do przeszukania wierzchołek o najmniejszej liczbie porządkowej. Dlatego szukając kolejny nieodwiedzony następnik należy rozpoczynać od końca macierzy. Przeszukiwanie DFS wykorzystuje się do badania spójności grafu. Jeśli procedura wywołana dla pierwszego wierzchołka "dotrze" do wszystkich wierzchołków grafu to graf jest spójny.
Aby przeszukać graf wszerz (BFS) należy zamiast stosu wykorzystać kolejkę do przechowywania wierzchołków a kolejnych nieodwiedzonych następników szukać od początku macierzy.

Przeszukanie grafu wszerz (BFS) pozwala wyznaczyć najkrótsze z możliwych ścieżek od ustalonego wierzchołka grafu s do wszystkich pozostałych wierzchołków grafu - w wyniku dla każdego wierzchołka u otrzymujemy jedną ze wszystkich ścieżek s-...-u o najkrótszej długości. Jeśli pomiędzy wierzchołkami s oraz u istnieje kilka takich ścieżek, to o wyborze ścieżki decyduje kolejność przetwarzania następników poszczególnych wierzchołków ścieżki.
Dodatkowo dla każdego wierzchołka grafu u algorytm wyznacza jego głębokość g[u] w stosunku do wierzchołka początkowego s, czyli długość znalezione najkrótszej ścieżki s-...-u. Przeszukanie wszerz wykonuje się przy pomocy kolejki, w której na początku umieszczamy wierzchołek startowy s. Każdemu składnikowi kolejki towarzyszy jego głębokość względem wierzchołka startowego s zapisana w tablicy głębokości g - ten pierwszy składnik kolejki, którym jest wierzchołek s zapisujemy z głębokością 0.
Algotytm musi mieć możliwość sprawdzania, dla których wierzchołków grafu wyznaczona została już najkrótsza ścieżka i jej długość. Przeszukanie grafu w głąb (DFS) polega na takim przejściu przez graf, aby każdy wierzchołek został odwiedzony dokładnie jeden raz - odwiedzane są wszystkie wierzchołki grafu, czyli odmiennie niż w przeszukiwaniu wszerz, gdzie odwiedzone zostaną tylko wierzchołki osiągalne z wierzchołka źródłowego. W odróżnieniu od algorytmu BFS przeszukiwanie w głąb jest algorytmem rekurencyjnym, pozwalającym zebrać sporo informacji o strukturze grafu.

Minimalne drzewo rozpinające

Niech będzie dany spójny graf nieskierowany o wierzchołkach V i krawędziach E. Ponad to z każdą krawędzią będzie związana tzw. waga, określna przez funkcję w, która oznaczają długość danej krawędzi. Jeżeli znajdziemy taki podzbiór T zawarty w zbiorze krawędzi E, który łączy wszystkie wierzchołki i taki, że suma wszystkich wag krawędzi wchodzących w skład T jest możliwie najmniejszy, to znajdziemy tzw. minimalne drzewo rozpinające. Oto minimalne drzewo rozpinające dla przykładowego grafu:

Suma wag dla tego drzewa wynosi 10

Jest znanych kilka algorytmów tworzące takie drzewo. Wszystkie one wykorzystują tzw. metodę "zachłanną". Do rozrastającego się drzewa dodawane są "najlepsze" krawędzie, w tym przypadku o najmniejszej wadze.

Algorytm Fermata to jedna z metod faktoryzacji, czyli rozkładu liczby na czynniki pierwsze. Metoda ta szybko znajduje rozkład n jeśli jego dzielniki są bliskie pierwiastkowi kwadratowemu z n. Z powodu istnienia tej metody, tworząc klucze kryptograficzne oparte na iloczynach liczb pierwszych (RSA), unika się iloczynów niewiele różniących się liczb.

Działanie algorytmu polega na szukaniu pary liczb a i b takich że

n = a² − b².

Tę różnicę można przedstawić jako iloczyn (a + b)(a − b); Jeśli żaden z tych czynników nie jest równy jeden, otrzymujemy faktoryzację n. Warto zauważyć że dla każdego nieparzystego n istnieje taka para liczb. Jeśli n=cd, to

n = [(c + d) / 2]² − [(c − d) / 2]².

W najgorszym przypadku algorytm Fermata może działać wolniej niż naiwne szukanie dzielników n, dlatego nie ma on praktycznego zastosowania. Jego zasada działania stanowi jednak podstawę znacznie efektywniejszych algorytmów faktoryzacji, takich jak sito kwadratowe i GNFS.

Pseudokod:

Wejście: liczba N

Wyjście: dzielnik liczby N najbliższy pierwiastkowi

Jeśli N jest kwadratem liczby naturalnej

return sqrt(N); /*Znaleziono dzielnik*/

w przeciwnym razie

r := sqrt(N);

e := r^2 - N;

u := 2r + 1; v := 1;

Dopóki nie znaleziono dzielnika

Jeśli e=0

return (u-v)/2; /*Znaleziono dzielnik*/

w przeciwnym razie

Dopóki e<>0

Dopóki e<0

e:=e+u;

u:=u+2;

Dopóki e>0

e:=e-v;

v:=v+2;

Algorytm Sito-Erastotenesa:

Około roku 200 p.n.e grecki matematyk Eratostenes podał algorytm na znajdowanie liczb pierwszych. Nazwa pochodzi od sposobu w jaki są one znajdowane. Wszystkie liczby po kolei przesiewa się - usuwane są spośród nich wszystkie wielokrotności danej liczby.

Przykład:
Odnajdziemy za pomocą sita Eratostenesa wszystkie liczby pierwsze z zakresu od 2 do 30.
Zapisujemy kolejno wszystkie liczby w tabeli.

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

Teraz bieżemy pierwszą liczbę z tabeli (2) i począwszy od następnej wykreślamy z niej wszystkie te liczby, które są przez nią podzielne.

2

3

5

7

9

11

13

15

17

19

21

23

25

27

29

Bieżemy kolejną liczbę (3) i począwszy od następnej wykreślamy z tabeli podzielne przez nią.

2

3

5

7

11

13

17

19

23

25

29

Kolejną liczbą w tabeli jest 5. Postępujemy jak poprzednio.

2

3

5

7

11

13

17

19

23

29

W tym momencie możemy zakończyć nasze poszukiwania. Algorytm "mówi", że kolejne wykreślania należy powtarzać, nie dalej jak do liczby będącej zaokrąglonym w dół pierwiastkiem zakresu. U nas jest to: sqrt(30)=5.4772255.., po zaokrągleniu w dół otrzymujemy 5. W tabeli zostały już tylko liczby pierwsze.

Złożoność obliczeniowa:

Jest to jeden z najważniejszych parametrów charakteryzujących algorytm. Decyduje on o efektywności całego programu. Podstawowymi zasobami systemowymi uwzględnianymi w analizie algorytmów są czas działania oraz obszar zajmowanej pamięci. Na złożoność czasową składają się dwie wartości: pesymistyczna, czyli taka, która charakteryzuje najgorszy przypadek działania oraz oczekiwana. Najczęściej algorytmy mają złożoność czasową proporcjonalną do funkcji:

• log(n)- złożoność logarytmiczna

• n - złożoność liniowa

• nlog(n) - złożoność liniowo-logarytmiczna

• n² - złożoność kwadratowa

• n^k - złożoność wielomianowa

• 2ⁿ - złożoność wykładnicza

• n! - złożoność wykładnicza, ponieważ n!>2ⁿ już od n=4

Algorytm Forda-Bellmana

Algorytm ten służy do wyznaczania najmniejszej odległości od ustalonego wierzchołka s do wszystkich pozostałych w skierowanym grafie bez cykli o ujemnej długości.
Warunek nieujemności cyklu jest spowodowany faktem, że w grafie o ujemnych cyklach najmniejsza odległość między niektórymi wierzchołkami jest nieokreślona, ponieważ zależy od liczby przejść w cyklu.
Dla podanego grafu macierz A dla każdej pary wierzchołków u i v zawiera wagę krawędzi (u,v), przy czym jeśli krawędź (u,v) nie istnieje, to przyjmujemy, że jej waga wynosi nieskończoność i wpisujemy *.
Algorytm Forda-Bellmana w każdym kroku oblicza górne oszacowanie D(v_i) odległości od wierzchołka s do wszystkich pozostałych wierzchołków v_i. W pierwszym kroku przyjmujemy D(v_i)=A(s,v_i).
Gdy stwierdzimy, że D(v)>D(u)+A(u,v), to każdorazowo polepszamy aktualne oszacowanie i podstawiamy D(v):=D(u)+A(u,v). Algorytm kończy się, gdy żadnego oszacowania nie można już poprawić, macierz D(v_i) zawiera najkrótsze odległości od wierzchołka s do wszystkich pozostałych.

Pseudokod wygląda następująco:(n- liczba wierzchołków)

begin;
for v:=[1..n] do D(v):=A(s,v); //przyjmujemy, że najkrótszą drogą z u do v jest krawędź (u,v)
for k:=1 to (n-2) do //w (n-2) krokach można zbadać każdą drogę o (n-1) krawędziach i wybrać najkrótszą
begin
for v:=[1..n]-{s} do //odległość od s do s wynosi 0 i już się na pewno nie zmieni
for u:=[1..n] do
D(v):=min{D(v), D(u)+A(u,v)}; //wybierz krótszą drogę
end;

Algorytm można ulepszyć sprawdzając w każdej iteracji, czy coś się zmieniło od poprzedniej i jeśli nie, to można zakończyć obliczenia.
Dla pełnej jasności podam teraz prosty przykład: oto graf i jego reprezentacja w postaci macierzy wag krawędzi.
Przyjmujemy s=1, symbol "*" oznacza nieskończoność:

Oto przebieg obliczeń:
Oto przebieg obliczeń:

k	D(1)	D(2)	D(3)	D(4)	D(5)	D(6)
0	0	2	4	*	*	*
1	0	2	4	2a	6b	4c
2	0	2	4	2	5d	4
3	0	2	4	2	5	4

Objaśnienia:
W pierwszym kroku (k=0) D(v_i)=A(1,v_i). Przepisujemy pierwszy wiersz macierzy wag krawędzi.
a). Pierwsze skrócenie drogi: w poprzednim kroku D(4)=*, gdyż nie istnieje krawędź od 1 do 4. Teraz jednak możemy przejść przez wierzchołek 3 (odległość od 1 do 3 wynosi 4) a następnie do 4 (waga krawędzi [3,4]=-2), długość drogi od 1 do 4 wynosi więc 4-2=2.
b). Podobnie jest tu, do wierzchołka 5 możemy dojść przez 2, 3, lub 6. Wybieramy oczywiście drogę o mniejszej długości:

• D(2)+A(2,5)=2+4=6 (ta wartość jest najmniejsza)

• D(3)+A(3,5)=4+3=7

• D(6)+A(6,5)=*+1 (ta wartość jest największa)

Wybieramy opcję z wierzchołkiem nr. 2.
c). Do wierzchołka 6 możemy dojść przez 4 (do którego dochodzimy przez 3) droga jest więc następująca: 1, 3, 4, 6 a jej długość wynosi D(4)+A(4,6)=2+2=4
d). Jak wynika z punktu b), do wierzchołka 5 możemy dojść także poprzez wierzchołek 6. W poprzednim kroku poznaliśmy odległość do wierzchołka 6 i nie wynosi ona już nieskończoność. Sprawdźmy więc, jaka byłaby długość drogi do wierzchołka 5 poprzez 6: D(6)+A(6,5)=4+1=5. Jest to wartość mniejsza niż aktualna (6), więc znaleliśmy krótszą drogę.
W kroku k=3 nic się nie zmieniło od kroku k=2. Kończymy obliczenia i mamy wektor najkrótszych dróg od wierzchołka s=1 do wszystkich pozostałych.
Złożoność obliczeniowa: O(n³).
Uwaga:
Dla grafów z wagami o nieujemnych wartościach lepiej jest stosować Algorytm Dijkstry.
Po znalezieniu najkrótszej odległości między wierzchołkami możemy znaleźć drogę łączącą te wierzchołki za pomocą algorytmu konstrukcji drogi.

Algorytm Dijkstry

Algorytm ten jest uogólnieniem algorytmu Dekker'a na większą liczbę procesów i wykorzystuje się go do rozwiązania problemu wzajemnego wykluczania. Z zagadnieniem tym mamy do czynienia na przykład, gdy równolegle wykonywane procesy korzystają ze wspólnej pamięci. Przeprowadźmy symulację działania dwóch równolegle wykonywanych programów, z których jeden zwiększa wartość współdzielonej zmiennej w o 2, a drugi o 3 (wartość początkowa w to 0). Najpierw obydwa procesy pobierają wartość zmiennej w po czym pierwszy zwiększa jej wartość o 2 (0+2=2), a drugi o 3 (0+3=3). Po wykonaniu operacji procesy odsyłają wyniki. Jeżeli proces pierwszy zapisze swój wynik szybciej do zmiennej współdzielonej końcowym wynikiem będzie 3, jeżeli wolniej niż proces drugi w wyniku otrzymamy 2. W przypadku, gdy procesy wykonają obliczenia w sposób, który wykluczy jednoczesny dostęp do zmiennej współdzielonej wynik będzie prawidłowy.

Zapiszmy teraz problem wzajemnego wykluczania w sposób formalny:
Dany jest zbiór procesów sekwencyjnych komunikujących się przez wspólną pamięć. Każdy z procesów zawiera sekcję krytycznę, w której następuje dostęp do wspólnej pamięci. Procesy te są procesami cyklicznymi. Zakłada sie ponadto:

• zapis i oczyt wspólnych danych jest operacją niepodzielną, a próba jednoczesnych zapisów lub odczytów realizowana jest sekwencyjnie w nieznanej kolejności

• sekcje krytyczne nie mają priorytetu,

• względne prędkości wykonywania procesów są nieznane,

• proces może zostać zawieszony poza sekcją krytyczna,

• procesy realizujące instrukcje poza sekcją krytyczną nie mogą uniemożliwiać innym procesom wejścia do sekcji krytycznej,

• procesy powinny uzyskac dostep do sekcji krytycznej w skonczonym czasie.

Założenia dotyczące algorytmu są następujące:
Algorytm pozwala rozwiązać problem wzajemnego wykluczania dla n procesów.
Do komunikacji między równolegle wykonującymi się procesami służą 2 współdzielone zmienne:
  flag[1..n] - która dla każdego procesu przyjmuje trzy możliwe wartości: 0 - proces znajduje się poza sekcją krytyczną, 1 - proces ubiega się o wejscie do sekcji krytycznej, 2 - proces albo jest w drugim etapie ubiegania się o dostęp do sekcji krytycznej, albo wykonuje zadania w sekcji krytycznej,
  turn - określa, który z procesów ma pierszeństwo wejścia do sekcji krytycznej.
Algorytm Dijkstry ma następującą postać (zmienna i przyjmuje wartość będącą numerem procesu, czyli w procesie pierwszym 1, w procesie drugim 2, ...):

procedure process_i;
var //zmienne lokalne procesu
test, k, other, temp: integer;
begin
  while true do
   begin
   {część prgramu przed sekcją krytyczną}
  L: flag[i]:=1;
   other:=turn;
   while other<>i do
    begin
    test:=flag[other];
    if test=0 then turn:=i;
    other:=turn;
    end;
   flag[i]:=2;
   for k:=1 to n do
    if k<>i then
     begin
     test:=flag[k];
     if test=2 then goto L;
     end;
   {sekcja krytyczna}
   flag[i]:=0;
   {pozostała część programu}
   end;
end;

W algorytmie tym wejście do sekcji krytycznej odbywa się dwuetapowo. Najpierw proces, ustawia swoją flagę na wartość 1. Następnie sprawdza, który z procesów ma pierszeństwo wejścia sekcji krytycznej. Jeżeli jest nim właśnie on, przechodzi do drugiego etapu (ustawia swoją flagę na wartość 2), w przeciwnym wypadku czeka, aż proces, który ma pierszeństwo wyjdzie z sekcji krytycznej (pierwsza pętla while). Jeżeli proces, który miał pierszeństwo nie znajduje się już w sekcji krytycznej, proces ubiegający się o wejście do niej ustawia pierszeństwo na siebie (instrukcja if w pierwszej pętli while).
W drugim etapie proces sprawdza flagi wszystkich pozostałych procesów. Jeżeli wykryje, że któryś z procesów dostał się razem z nim do drugiego etapu następuje powrót do etapu pierwszego (instrukcja goto). Jeżeli natomiast proces ten jest jedynym procesem w drugim etapie, może on wejść do sekcji krytycznej.
Po wyjściu z sekcji krytycznej proces zdejmuje falgę (ustawia wartość zmiennej współdzielonej flag[i], na wartość 0), ustępując tym samym miejsce procesom czekającym w pierwszym etapie.
W skrajnym przypadku proces może nie uzyskać dostępu do sekcji krytycznej, gdyż inne (szybsze) procesy mogą go blokować w pierwszej z pętli while.

Algorytm KR (Karpa-Rabina)

Podstawowym problemem dotyczącym tekstów jest problem wyszukiwania wzorca. Polega on na znalezieniu wszystkich wystąpień tekstu wzorzec, w tekście tekst. Przyjmujemy ponadto, że: |wzorzec|=m, |tekst|=n oraz n>=m.

W Algorytmie tym stosujemy funkcję haszującą (mieszającą) h, dzięki, której będziemy obliczać pewną wartość (kod) podsłowa tekst_i=tekst[i..i+m-1] tekstu wejściowego. Jeśli h(tekst_i)=h(wzorzec), to z bardzo dużym prawdopodobieństwem wzorzec występuje w tekscie na i-tym miejscu. Efektywność algorytmu wynika z możliwości szybkiego obliczenia wartości h(tekst_i+1), jeżeli wartość h(tekst_i) jest już znana.
Zakładamy, że alfabet składa się z r symboli i każdemu z nich przypisana jest wartość liczbowa (np.: z tablicy znaków ASCII). Niech q będzie pewną, bardzo dużą liczbą pierwszą (np.: taką, że q(r+1) nie powoduje nadmiaru). Jeśli z jest tekstem o długości m, to wówczas funkcję haszującą h definiujemy jako: h(z)=(z[1]r^m-1+z[2]r^m-2+ ... +z[m]) mod q
Prawdopodobieństwo, że wartości h będą takie same dla dwóch różnych argumentów jest bardzo małe i wynosi: 1/q, gdyż należy pamiętać, że q jest bardzo duże. W oryginalnej wersji liczba pierwsza q wybierana jest losowo. Do znajdowania liczb pierwszych zastosować możemy sito Eratostenesa.

Algorytm ma postać:
h1=h(wzorzec);
rm=r^m-1;
h2=h(tekst[1..m]);
while i<=n-m+1 do
begin
  j:=0;
  if h2=h1 then while ((j<m)and(wzorzec[j+1]=tekst[i+j])) do j:=j+1;
  if j=m then writeln((IntToStr(i)));//wypisanie indeksu, w którym istnieje dopasowanie
  h2:=((h2-tekst[i])*rm) * r + tekst[i+m]) mod q;
  i:=i+1;
end;

W pierwszej i trzeciej lini algorytmu do obliczenia wartości h1 oraz h2 możemy użyć algorytmu Hornera. W literaturze spotkać można się z określeniem, iż algorytm KR jest agorytmem praktycznym. Należy jednak podkreślić, że możemy napotkać trudności podczas obliczania dużych wartości. Na przykła dla alfabetu złożonego z wszystkich znaków ASCII (256) i wzorca długości 10 znaków zmienna rm ma wartość 1208925819614629174706174, należałoby zatem użyć algorytmu szybkiego potęgowania modularnego.

Tablice z hashowaniem

Tablice z hashowaniem są stosowane, gdy z pewnego dużego zbioru danych w danej chwili musimy znać stosunkowo jego niewielki podzbiór. Elementy z tego podzbioru są zapisywane w tablicy, której indeksy dla danego elementu oblicza specjalna funkcja hashująca. Takie rozwiązanie zmniejsza złożoność pamięciową algorytmy, np. wyobraźmy sobie, że ze zbioru 10.000 liczb całkowitych w danej chwili potrzebujemy jedynie 10. Po zastosowaniu tablicy z hashowaniem zmniejszamy wymaganą pamięć 1000-krotnie. Ponieważ adres danego elementu jest obliczany na podstawie jego wartości, funkcja hashująca jest bardzo szybka. Jednak z tego samego powodu może dojść do konfliktu. Może się bowiem zdarzyć tak, że funkcja wyznaczy kilku danym tą samą komórkę w pamięci. Jest to niedopuszczalne, należy więc w takim przypadku do komórki wyznaczonej przez funkcję doczepić statyczną tablicę o ilości elementów równej ilości przydzielonych komórce elementów. Ponieważ tablice są statyczne, algorytm nie traci na szybkości, a ponieważ każdy element ma osobne w niej miejsce nie dochodzi do konfliktu.

Jeśli funkcja hashująca wyznaczy wszystkim elementom tą samą komórkę, elementy te zostaną zapisane w jednej tablicy. W najgorszym przypadku więc tablica z hashowaniem sprowadza się do zwykłej tablicy statycznej (stąd złożoność pesymistyczna przeszukiwania jest O(n)). Jeśli jednak funkcja hashująca wyznaczy każdemu elementowi inny adres złożoność przeszukiwania jest stała: O(1), (wynika to z faktu, że wartość szukanego elementu jest jednoznaczna z jego adresem w pamięci). Jednym z najczęściej przytaczanych przykładów zastosowania tablicy z hashowaniem są kompilatory. Podczas analizowania programu muszą one zapamiętywać, czy dana zmienna już wystąpiła, a jeśli tak, to co znaczy.
Podstawą tablic z hashowaniem jest dobra funkcja hashująca. Miarą tej "dobroci" jest stopień, w jakim spełnia ona zasadę prostego równomiernego hashowania, tzn: losowo wybrany klucz jest z takim samym prawdopodobieństwem odwzorowywany na każdą z pozycji. Oznacza to poprosty, by klucze były w miarę równomiernie rozpraszane w tablicy.
Jedną z najprostszych funkcji hashujących jest funkcja modularna, która dla klucza k zwraca wartość reszty z dzielenia k przez m (m-długość tablicy), czyli h(k)=k modulo m.
Funkcja hashująca dla hasowania modularnego może wyglądać następująco:

#include <math.h>
...
int h(int x){
return fmod(x, m);
}

Aby funkcja modularna dawała zadowalające efekty należy dobrać odpowiednią wartość m: nie powinna być ona potęgądwójki. Dlatego należy wybierać liczby pierwsze dalego położóne od potęg dwójki, np. dobrą wartością jest m=701.

---