3.3 Kwartyle.

Niech
będzie uporządkowanym niemalejąco ciągiem wartości badanej cechy. Tworzymy dwie grupy:

• grupa I -
  ,

• grupa II -
  .

Kwartylem pierwszym (dolnym)
nazywamy medianę pierwszej grupy, a kwartylem trzecim (górnym)
nazywamy medianę drugiej grupy. Zgodnie z tymi określeniami mediana jest kwartylem drugim.

W naszym przykładzie, w przypadku cechy skokowej
- staż pracy,
. Zatem pierwsza grupa zawiera 18 wartości ustawionych w ciągu niemalejącym od
do
. Zgodnie z wzorem na medianę mamy więc

,

co oznacza, że co najmniej 25% pracowników pracuje nie więcej niż 2,5 roku oraz co najmniej 75% pracowników pracuje nie mniej niż 2,5 roku.

Druga grupa zawiera również 18 wartości ustawionych w ciągu niemalejącym od
do
. Można ten ciąg przenumerować, tzn. przyjąć
...
. Wtedy mamy

,

co oznacza, że co najmniej 75% pracowników pracuje nie więcej niż 4 lata oraz co najmniej 25% pracowników pracuje nie mniej niż 4 lata.

W przypadku cechy ciągłej
- dziennej wydajności pracy otrzymaliśmy
. Mamy więc analogicznie

,

co oznacza, że dla co najmniej 25% pracowników dzienna wydajność jest nie większa niż 152,5 sztuki oraz dla co najmniej 75% pracowników nie mniejsza niż 152,5 sztuki,

.

co oznacza, że dla co najmniej 75% pracowników dzienna wydajność jest nie większa niż 255 sztuk oraz dla co najmniej 25% pracowników nie mniejsza niż 255 sztuk.

Kwartyl pierwszy i kwartyl trzeci można także wyznaczyć, w przypadku cechy skokowej, korzystając z szeregu rozdzielczego tej cechy:
. Kwartyl pierwszy jest to wartość cechy, dla której - jako pierwszej - liczebność skumulowana przyjmuje wartość co najmniej
, tzn.

,

albo, częstość skumulowana przyjmuje wartość co najmniej
, tzn.

.

Kwartyl trzeci jest to wartość cechy, dla której - jako pierwszej - liczebność skumulowana przyjmuje wartość co najmniej
, tzn.

,

albo, częstość skumulowana przyjmuje wartość co najmniej
, tzn.

.

Wobec tego, z tabeli

2	9	9
3	12	21
4	6	27
5	4	31
6	4	35
	35	Xxx

albo, z tabeli

2	0,2571	0,2571
3	0,3429	0,6000
4	0,1714	0,7714
5	0,1143	0,8857
6	0,1143	1,0000
	1,0000	Xxx

wynika, że
oraz
.

Korzystając z szeregu rozdzielczego cechy ciągłej:
oraz wzorów

,
,

albo

,
,

można odczytać tylko przedział, do którego należą kwartyle. Mianowicie, z tabeli

90 - 160	11	11
160 - 230	13	24
230 - 300	4	28
300 - 370	5	33
370 - 440	2	35
	35	xxx

oraz

90 - 160	0,3143	0,3143
160 - 230	0,3714	0,6857
230 - 300	0,1143	0,8000
300 - 370	0,1429	0,9429
370 - 440	0,0571	1,0000
	1,0000	xxx

można stwierdzić, że

,
.

W celu wyznaczenia wartości kwartyla pierwszego korzysta się z wzoru interpolacyjnego

,

gdzie:

- numer przedziału, do którego należy kwartyl pierwszy,

- dolna granica przedziału, do którego należy kwartyl pierwszy,

- rozpiętość przedziału, do którego należy kwartyl pierwszy,

- liczebność przedziału, do którego należy kwartyl pierwszy,

- suma liczebności przedziałów poprzedzających przedział, do którego należy kwartyl pierwszy.

Uwaga Jeżeli
, to
.

W naszym przykładzie mamy kolejno:
,
,
,
,
. Zatem

.

W celu wyznaczenia wartości kwartyla trzeciego korzysta się z wzoru interpolacyjnego

,

gdzie:

- numer przedziału, do którego należy kwartyl trzeci,

- dolna granica przedziału, do którego należy kwartyl trzeci,

- rozpiętość przedziału, do którego należy kwartyl trzeci,

- liczebność przedziału, do którego należy kwartyl trzeci,

- suma liczebności przedziałów poprzedzających przedział, do którego należy kwartyl trzeci.

W naszym przykładzie mamy kolejno:
,
,
,
,
. Zatem

.

Stosując moduł Statystyki opisowe pakietu STATISTICA 6.0 można otrzymać wartości kwartyli badanych cech (stażu pracy i dziennej wydajności). Mianowicie mamy:

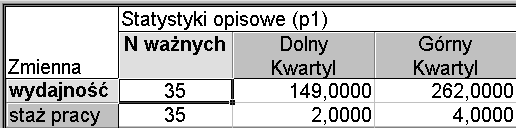
W przypadku cechy skokowej wartości kwartyli odczytane z ciągu, odczytane z tabeli szeregu rozdzielczego i podane przez program STATISTICA 6.0 są w zasadzie takie same. W przypadku cechy ciągłej wartości kwartyli są zdecydowanie różne, co oznacza, że ich wartość zależy od sposobu wyznaczania.

3.4 Dominanta.

Dominantą (modą, wartością modalną) nazywamy najczęściej powtarzającą się wartość, o ile istnieje. Dominantę oznaczamy
.

W przypadku danych indywidualnych cechy skokowej:
, nietrudno stwierdzić, że
, co oznacza, że w rozważanej próbie dominują pracownicy o 3-letnim stażu pracy. Analogiczny rezultat można otrzymać, analizując szereg rozdzielczy tej cechy:
.

W przypadku danych indywidualnych cechy ciągłej:
, kilka wartości(125, 145, 149, 168, 192) powtarza się dwa razy, pozostałe występują jednokrotnie. Trzeba zatem przyjąć zasadę, że w przypadku cechy ciągłej dominanty nie wyznacza się z danych indywidualnych.

Weźmy więc szereg rozdzielczy tej cechy:
. Korzystając z tabeli

90 - 160	11
160 - 230	13
230 - 300	4
300 - 370	5
370 - 440	2
	35

można stwierdzić, że dominującym przedziałem (przedziałem o największej liczebności) jest
.

W celu wyznaczenia wartości dominanty korzystamy z wzoru interpolacyjnego

,

gdzie:

- numer przedziału, w którym znajduje się dominanta,

- dolna granica przedziału, w którym znajduje się dominanta,

- rozpiętość przedziału, w którym znajduje się dominanta,

- liczebność przedziału, w którym znajduje się dominanta,

- liczebność przedziału poprzedniego,

- liczebność przedziału następnego.

Uwaga Jeżeli
, to
, a jeżeli
, to
.

W naszym przykładzie mamy kolejno:
,
,
,
,
,
. Wobec tego

,

co oznacza, że przybliżoną wartością najbardziej typowych wydajności pracy jest 175,56.

Stosując moduł Statystyki opisowe pakietu STATISTICA 6.0 można otrzymać wartości dominanty (mody) badanych cech (stażu pracy i dziennej wydajności). Mianowicie mamy:

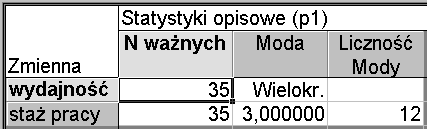
Relacją pozwalającą na przybliżone wyznaczenie jednego z trzech parametrów: średnia, mediana, dominanta, jeżeli znamy dwa pozostałe jest wzór Pearsona

.

Wzór ten daje dobre rezultaty w rozkładach zbliżonych do symetrycznych.

Rozważmy przykład.

Przykład 2. Czas tygodniowo poświęcany przez studentów na pracę w czytelni (w godz.) podany jest w tabeli szeregu rozdzielczego:

2 - 4	3	2
4 - 6	5	3
6 - 8	7	10
8 - 10	9	8
10 - 12	11	2
	xxx	25

Obliczymy średni czas pracy w czytelni

godz.

oraz medianę

godz.

Korzystając teraz z wzoru Pearsona, zapisanego w postaci

możemy obliczyć dominantę, a mianowicie

godz.

Sprawdzimy, ile wynosi dominanta liczona według wzoru na dominantę

godz.

---