Politechnika Wrocławska

Wydział Elektroniki Mikrosystemów i Fotoniki (W-12)

Kurs: ETD 4031C - Technika Analogowa 2

• Ćwiczenia rok: 2003/04

• Karol Kozan 117751 II/EIT

• Zadanie Z13-1

• Treść:

W sieci przedstawionej na rys.1 obliczyć prąd i(t), za pomocą twierdzenia Thevenina. Warunki początkowe zerowe.

• Dane: R₁=R₂=R₀=1; L=1; C=1; e(t)=2e^-t1(t).

rys.1

• Teoria:

Stanem nieustalonym nazywamy stan liniowej sieci (SLS) elektrycznej , który charakteryzuje przejście od jednego do drugiego stanu ustalonego.

W zadaniu mamy wykorzystać metodę operatorową .Poniższy schemat obrazuje jak przebiega proces rozwiązywania zadań tą metoda (rys.2).

rys.2

• Rozwiązanie: Obwód z rys.1 można zastąpić schematem operatorowym przedstawionym na rys.3

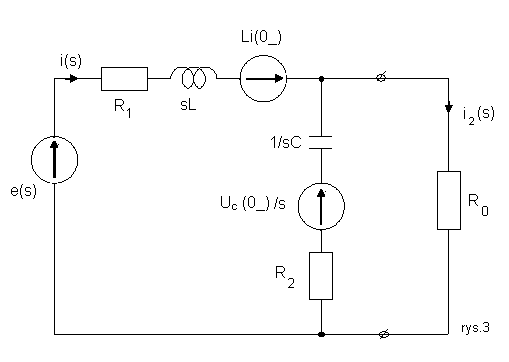
Ponieważ warunki początkowe są równe zero mamy :

• U_c(0_) = 0 wiec
  

• i(0_) = 0 więc
  

• e(t)=2e^-t1(t) - zmieniamy to w dziedzinę transformaty Laplace`a

₤{f(t)1(t)}=F(s) ; ₤{2e^-t1(t)}=

Aby wyznaczyć wartość prądu i₂(s) korzystając z twierdzenia Thevenina musimy powyższy układ zastąpić, zgodnie z tym twierdzeniem, dwójnikiem składającym się z siły elektromotorycznej e_z(s) i szeregowo dołączonej impedancji Z_w(s) (rys.4).

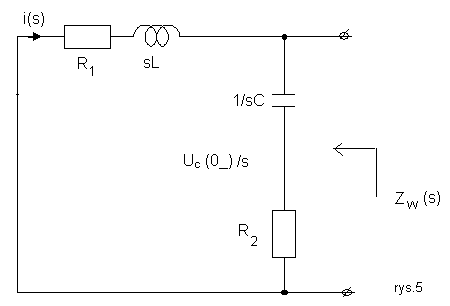
e_z(s) - jest to wartość napięcia na rozwartych zaciskach (rys.5).

Z_w(s) - jest to impedancja zastępcza naszego obwodu(dwójnika) mierzona na rozwartych zaciskach kiedy wszystkie źródła napięciowe są zwarte (rys.6).

rys.4

Obliczenia:

• Z_w(s)

• e_w(s)

Korzystając z II prawa Kirchoffa otrzymujemy:

Po wyliczeniu Z_w(s) i e_z(s) mamy następujący układ (rys.7). Teraz korzystając z prawa Ohma można łatwo wyliczyć szukany prąd i₂(s).

Teraz wystarczy zastosować odwrotną przekształcenie Laplace`a :

₤^-1{F(s)} = f(t)1(t)

=₤^-1= te^-t1(t)

i(t) = te^-t1(t)

• Literatura:

• Notatki z wykładu Technika Analogowa 2

---