Algorytm jest przepisem opisującym krok po kroku rozwiązanie problemu lub osiągnięcie jakiegoś celu.

Algorytm gotowania jajka na miękko. Krok 1. Włóż jajko do gotującej się wody. Krok 2. Zanotuj czas początkowy t₀.

Krok 3. Oczytaj czas aktualny t. Krok 4. Oblicz  t = t - t₀. Krok 5. Jeśli  t < 3 min., to przejdź do kroku 3.

Krok 6. Wyjmij jajko z gotującej się wody. Zakończ algorytm.

Sposoby przedstawiania algorytmów

Występują następujące sposoby przedstawiania algorytmów:

1.Słowny – na ogół mało dokładny. 2. Lista kroków. 3. Schemat blokowy. 4. Drzewo algorytmu.

Zadanie {obliczanie wartości funkcji f(x)}:

Napisz algorytm obliczający wartość funkcji

przy założeniu, że dla x=0 f(x)=0 .

1. 
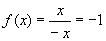
   Słowny opis algorytmu

a. dla liczb ujemnych |x| = -x, a więc

b. dla liczb dodatnich |x| = x, a więc

c. jeśli x = 0, to z podanej wyżej definicji

wynika, że f(x) = 0.

W matematyce opis słowny przedstawiamy następująco:

2. Algorytm w postaci listy kroków

Dane: Dowolna liczba rzeczywista x. Wynik: Wartość funkcji f(x) Krok 1. Wczytaj wartość danej x. Krok 2. Jeśli x > 0, to f(x)=1. Zakończ algorytm. Krok 3. Jeśli x = 0, to f(x)=0. Zakończ algorytm. Krok 4. Jeśli x < 0, to f(x)=-1. Zakończ algorytm.

3. Schemat blokowy 4. Drzewo algorytmu

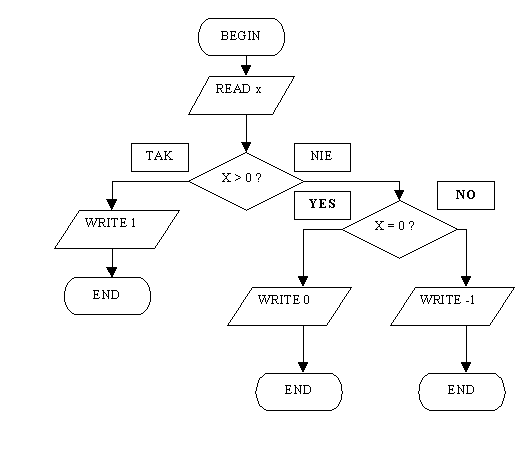
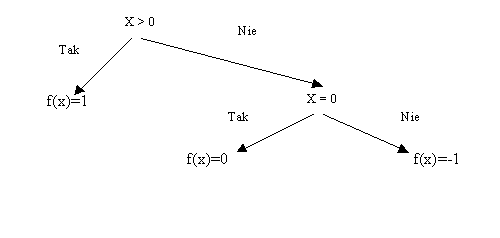
Program komputerowy to algorytm napisany w języku programowania. Blok decyzyjny ze schematu blokowego jest tutaj zastąpiony przez instrukcji if... then .... else....

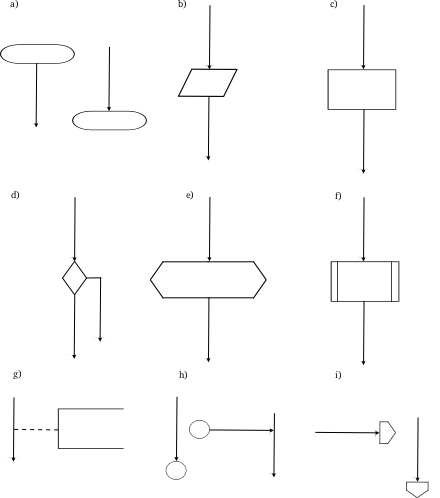
Schemat blokowy - diagram, na którym procedura, system albo program komputerowy są reprezentowane przez opisane figury geometryczne, połączone liniami zgodnie z kolejnością wykonywania czynności wynikających z przyjętego algorytmu rozwiązania zadania. Schemat blokowy pozwala dostrzec istotne etapy algorytmu i logiczne zależności między nimi. Zależnie od przedstawianego algorytmu stosowane są różne zestawy figur geometrycznych zwanych blokami, których kształty reprezentują umownie rodzaje elementów składowych. Wyróżnia się następujące rodzaje bloków: Graficzne przedstawienie bloków w kolejności opisywania. a) Blok graniczny - oznacza on początek, koniec, przerwanie lub wstrzymanie wykonywania działania, np. blok startu programu.b) Blok wejścia-wyjścia - przedstawia czynność wprowadzania danych do programu i przyporządkowania ich zmiennym dla późniejszego wykorzystania, jak i wyprowadzenia wyników obliczeń, np. czytaj z, pisz z+10. c) Blok obliczeniowy - oznacza wykonanie operacji, w efekcie której zmienią się wartości, postać lub miejsce zapisu danych, np. z = z + 1. d) Blok decyzyjny - przedstawia wybór jednego z dwóch wariantów wykonywania programu na podstawie sprawdzenia warunku wpisanego w ów blok, np. a = b. e) Blok wywołania podprogramu - oznacza zmianę wykonywanej czynności na skutek wywołania podprogramu, np. MAX(x,y,z). f) Blok fragmentu - przedstawia część programu zdefiniowanego odrębnie, np. sortowanie. g)Blok komentarza - pozwala wprowadzać komentarze wyjaśniające poszczególne części schematu, co ułatwia zrozumienie go czytającemu, np. wprowadzenie danych. h)Łącznik wewnętrzny - służy do łączenia odrębnych części schematu znajdujących się na tej samej stronie, powiązane ze sobą łączniki oznaczone są tym samym napisem, np. A1, 7. i) Łącznik zewnętrzny - służy do łączenia odrębnych części schematu znajdujących się na odrębnych stronach, powinien być opisany jak łącznik wewnętrzny, poza tym powinien zawierać numer strony, do której się odwołuje, np. 4.3, 2,B2. ]

Żeby przekazać posiadany algorytm drugiemu człowiekowi lub maszynie, musimy ten algorytm zapisać. I tu powstaje problem języka do zapisywania algorytmów. Języki naturalne, takie jak język polski, język angielski itp., nie bardzo się nadają do tego celu. Mimo to od wieków algorytmy zapisywano w językach naturalnych. Problem nie był palący, dopóki nie pojawiły się komputery. Ponieważ maszyna nie potrafi się niczego domyślić, to musi mieć jednoznacznie opisane czynności. Najlepszymobecnie “językiem” opisu algorytmów jest tzw. schemat blokowy.

Algorytmem liniowym nazywamy taki algorytm, który ma postać listy kroków wykonywanych zgodnie z ich kolejnością. Algorytmy liniowe są zapisem obliczeń, które mają postać ciągu operacji rachunkowych wykonywanych bez sprawdzania jakichkolwiek warunków.Wielomiany występują w wielu szkolnych zadaniach z matematyki oraz fizyki. Wartości wielomianów obliczmy dla konkretnych argumentów. Na ogół zajmujemy się wielomianami drugiego lub trzeciego stopnia, są to więc funkcje tak proste, że bez zastanowienia wykonujemy zapisane w nich działania

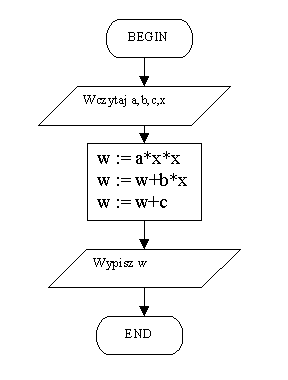
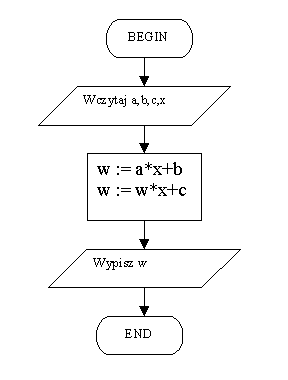
Algorytm zwykły obliczający wielomian II stopnia Algorytm Hornera obliczający wielomian II stopnia

Algorytm zwykły obliczający wielomian III stopnia (3 dodawania i 6 mnożeń)Aby zmniejszyć liczbę mnożeń, wykorzystamy przekształcenie wielomianu w(x) do następującej postaci:

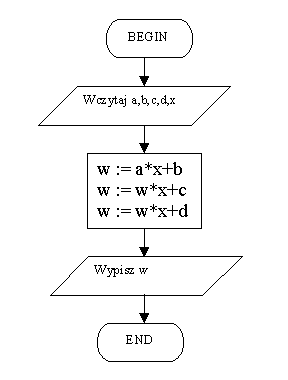
Algorytm Hornera obliczający wielomian III stopnia (3 dodawania i 3 mnożenia) Nie jest ważne, czy do obliczeń wykorzystamy liczydło, kalkulator lub superkomputer. Istotna jest metoda, którą zastosujemy do obliczeń, szczególnie gdy stopień wielomianu jest duży. Pokazuje to tabelka:

Wzór na liczbę mnożeń dla metody zwykłej

Wzór na liczbę mnożeń dla metody Hornera

Języki programowania dzielimy na: a) języki wewnętrzne (binarne lub asemblery), b) języki zewnętrzne (FORTRAN, COBOL, PASCAL, C, BASIC,CLIPPER).

Schematów blokowych używamy do zapisywania algorytmów głównie w komunikacji człowiek – człowiek. Natomiast w komunikacji człowiek – komputer, algorytmy zapisujemy przy pomocy tzw. języków programowania. Schematy blokowe są na razie “nieczytelne” dla komputerów, z powodu braku odpowiednich programów tłumaczących (translatorów) z postaci schematu blokowego na języki wewnętrzne komputerów.

Teraz możemy przystąpić do konstruowania programu, która będzie wykonywać nasz algorytm. Aby nie komplikować zbytnio naszego przykładu, zajmiemy się programowaniem algorytmu obliczającego wartość bezwzględną dla liczby x. Przyk. Program który przedstawia rozwiązanie

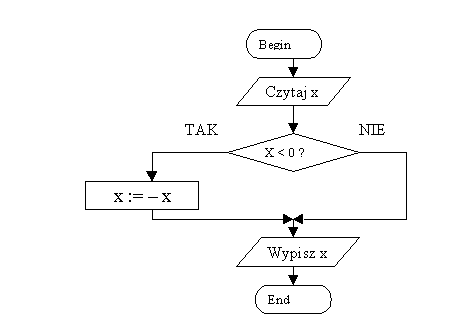
program WARTBEZ;

var x: real;

Begin

Read(x);

If( x < 0) then x := - x;

Else Write(x); END.

PROGRAM Aby zamienić schemat blokowy na zapis w postaci programu komputerowego będziemy musieli poznać budowę programu, w naszym przypadku napisanego w języku PASCAL. Każdy program w języku PASCAL, w pierwszym wierszu musi rozpoczynać się od napisu program, spacji, dowolnej nazwy programu oraz znaku średnika ;. W następnym wierszu należy zadeklarować jakich zmiennych będzie używał program. Deklaracja ta składa się z: napisu var, spacji, nazw zmiennych (np. x,y,z), znaku dwukropka :, typu zmiennej np. real (liczby rzeczywiste) oraz znaku średnika ;. (patrz poniższy przykład)

a.Czytania danych z klawiatury, Read(x);

b. Wypisywania wyników na ekranie, Write(y);

c. Badania warunku IF warunek THEN instrukcja1 ELSE instrukcja 2 ;

---