76. EFEKT HALLA

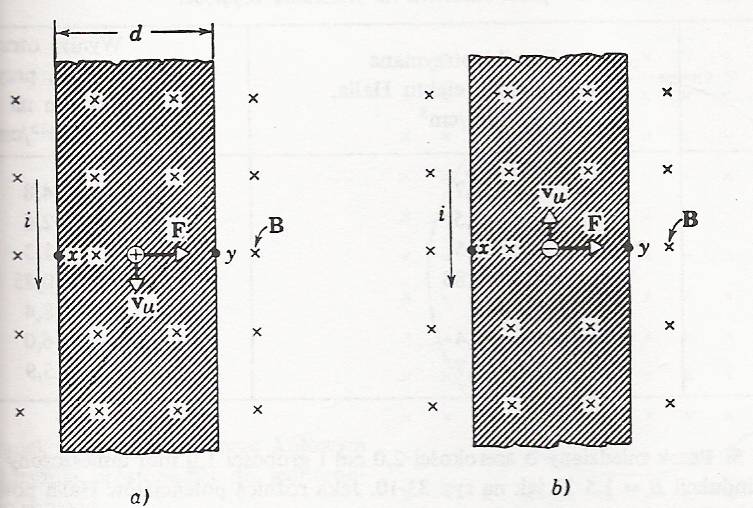
W pasku miedzianym umieszczonym w polu magnetycznym o indukcji B płynie prąd o natężeniu i, przy czym prąd jest przenoszony przez (a) ładunki dodatnie, (b) ujemne

Na ładunek elektryczny e poruszający się z prędkością v w polu magnetycznym B działa, jak wiadomo, siła Lorentza:

której kierunek jest prostopadły do wektorów v i B, a zwrot będzie zależał także od znaku ładunku e. Siła ta powoduje odchylanie się nośników ładunku tworzących prąd I w kierunku poprzecznym do kierunku przepływu prądu I i prostopadłym do pola magnetycznego B. Spowoduje to wystąpienie gradientu koncentracji nośników ładunku w tymże kierunku i pojawienie się wywołanego tym gradientem pola elektrycznego i tzw. Napięcia Halla V_H. Poprzeczne pole elektryczne E_H powstałe wskutek rozdzielenia ładunków dodatnich i ujemnych spowoduje wystąpienie dodatkowej siły działającej na nośniki prądu. Po ustaleniu się stanu równowagi, w którym odchylające pole magnetyczne jest równoważone przez pole elektryczne Halla (elektrony płyną prostoliniowo przez płytkę).

ponieważ napięcie pomiędzy dwoma punktami w polu elektrycznym jest równe iloczynowi natężenia tego pola i odległości pomiędzy punktami, a także z geometrii układu (prostopadłość wektorów v, B i E_H) mamy:

V_xy= v_u B

Wyrażając v przez gęstość prądu,

gdzie j oznacza gęstość prądu,

e wielkość ładunku elementarnego

średnią w czasie z tzw. prędkości unoszenia.

lub

Możemy znając E_H, B oraz gęstość prądu­­ wyznaczyć koncentrację nośników n.

CZĘSTOŚĆ CYKLOTRONOWA

Jest to częstość kołowa obiegu cząstki naładowanej w jednorodnym polu magnetycznym. Zależy ona od indukcji magnetycznej B, masy cząstki m oraz wielkości ładunku elektrycznego q.

Na cząstkę poruszającą się prostopadle do pola magnetycznego działa siła prostopadła do prędkości i pola magnetycznego, siła ta pełni rolę siły dośrodkowej:

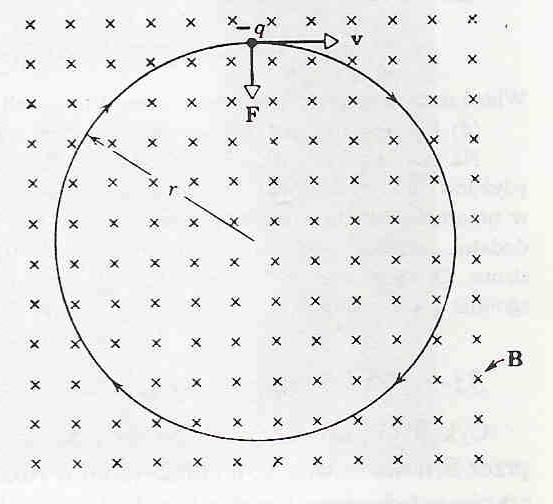
czyli

r- promień toru

prędkość kołowa ω jest równa v/r, czyli:

V nie zależy od prędkości cząstki. Szybkie poruszają się po dużych kołach, wolne po małych, ale każda z nich potrzebuje tego samego czasu T (okres), aby wykonać jeden obrót w polu.

Częstość v jest częstością charakterystyczną dla naładowanej cząstki w polu magnetycznym.

77. DOŚWIADCZENIE THOMSONA- odkrycie elektronu

Dotyczyło pomiaru stosunku ładunku e do masy elektronu m. doświadczenie polegało na pomiarze odchylenia naładowanych obiektów poruszających się w polach magnetycznym i elektrycznym. W ten sposób odkryto elektron jako cząstkę elementarną.

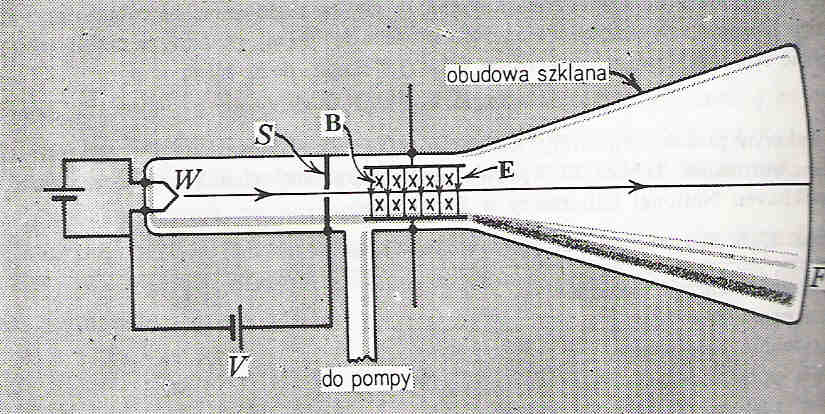
Rozżarzona e włókno W emituje elektrony, które są przyspieszane dzięki przyłożonej różnicy potencjałów V, następnie wpadają one do obszaru, w którym poruszają się prostopadle do pola elektrycznego E i magnetycznego o indukcji B. Wektory E i B są również prostopadłe do siebie. Gdy strumień elektronów uderzy w ekran fluoryzujący F, na ekranie widzimy plamkę. W całym obszarze w którym poruszają się Elektrony jest próżnia, dzięki czemu nie ma zderzeń z cząsteczkami .

Całkowita siła działająca na naładowaną cząstkę poruszającą się wpolu elektrycznym i magnetycznym :

F=q₀E+q₀v×B

Z rys. pole elektryczne odchyla czastki do góry, a magnetyczne do dołu. Jeżeli siły odchylające równoważą się (tzn. F=0) :

eE=evB

E=vB

Doświadczenie Thomsona polegało na:

(a) zanotowaniu położenia plamki nie odchylonej przy E i B jednocześnie równych zeru;

(b) zmierzeniu odchylenia plamki na ekranie fluoryzującym gdy przyłożone było stałe pole elektryczne E;

(c) przyłożeniu pola magnetycznego i dobraniu takiej jego wartości, żeby plamka z powrotem wróciła do położenia zerowego.

Odchylenie y elektronu w stałym polu elektrycznym (b), mierzone przy krawędzi płytki odchylającej:

v- prędkość elektronu,

l- długość płytek odchylających

Jeżeli (c) siła elektryczna jest równa co do wielkości, lecz przeciwnie skierowana niż siła magnetyczna, wypadkowa tych sił równa się zeru:

Wstawiając to równanie do równania na y i rozwiązując to ostatnie względem e/m otrzymujemy:

Wszystkie wielkości z prawej strony można zmierzyć. Otrzymana przez Thomsona wartość stosunku e/m wynosiła 1,7*10¹¹ C/kg

78. PRAWO AMPERE'A (przykład: oddziaływanie dwóch przewodników z prądem)

„Wartość całki okrężnej wektora natężenia pola magnetycznego, wytworzonego przez stały prąd elektryczny w przewodniku wzdłuż linii zamkniętej otaczającej prąd, jest równa sumie algebraicznej natężeń prądów obejmowanych przez tę linię.”

Wartości wektora indukcji magnetycznej w odległości r od nieskończenie długiego przewodnika, w którym płynie prąd o natężeniu I.

Obliczamy całkę po okręgu o promieniu r współśrodkowym z przewodnikiem:

Wartość wektora indukcji w odległości r od przewodnika wynosi więc:

Wektor ten jest styczny w danym punkcie do okręgu, po którym wykonane zostało całkowanie.

DWA PRZEWODNIKI RÓWNOLEGŁE:

Dwa równoległe przewodniki rozsunięte na odległość d, w których płyną prady o natężeniach i₁ i i₂.

Przewodnik a, wytwarza w swoim otoczeniu pole o indukcji B_a wytworzonego prze prąd i_a w miejscu, gdzie znajduje się drugi przewodnik wynosi:

Z reguły prawej ręki wynika ze w pobliżu przewodnika b, B_a jest skierowane w dół (rys.)

Przewodnik b, w którym płynie prąd i_b, umieszczony jest w zewnętrznym polu magnetycznym o indukcji B_a. Na odcinek l tego przewodnika działać będzie skierowana w bok siła magnetyczna (=il×B)

O wartości:

(Siła działająca na przewodnik a :
),

Siła dla prądów równoległych skierowana w prawą stronę.

Siły, jakimi działają siebie dwa przewodniki, są sobie równe co do wartości i przeciwnie skierowane

( zgodnie z newtonowską zasadą akcji i reakcji).

79. PRAWO BIOTA-SAVARTA

Element prądu dl wytwarza w punkcie P pole magnetyczne o indukcji dB, której wartość liczbowa wynosi:

Prawo Biota-Savarta w postaci wektorowej:

Wypadkową indukcję magnetyczną
w punkcie P znajdujemy sumując przyczynki od poszczególnych odcinków dl:

80. DIPOL MAGNETYCZNY

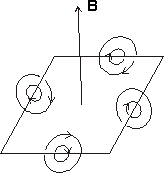
Dipolem magnetycznym nazywamy układ dwóch biegunów magnetycznych, jednakowych co do wartości, ale przeciwnych znaków, znajdujących się w odległości l. Dipol magnetyczny charakteryzuje wielkość zwaną dipolowym momentem magnetycznym μ.

(a)układ umieszczony w zewnętrznym polu magnetycznym obraca się pod wpływem

momentu skręcającego τ= μ×B

(b)układ sam wytwarza pole magnetyczne,

Przykładem dipola magnetycznego może być magnes trwały lub ramka z prądem elektrycznym.

Pole magnetyczne dipola.

Pole magnetyczne dipola przedstawiamy graficznie za pomocą linii pola. Przyjęto umownie, że linie pola mają zwrot siły działającej na biegun północny, umieszczony w tym polu.

• Linie pola są zawsze krzywymi zamkniętymi.

• Linie sił wokół prostego przewodnika z prądem maja kształt koncentrycznych kół, obejmujących przewodnik.

• Ich zwrot jest zgodny z kierunkiem obrotu śruby prawoskrętnej, wkręcanej w kierunku zgodnym z kierunkiem przepływu prądu.

• Siłową charakterystykę pola magnetycznego stanowi wektor indukcji magnetycznej B.

• Wektor indukcji jest w każdym punkcie styczny do linii pola magnetycznego. Wartość indukcji magnetycznej zależna jest od gęstości linii sił pola magnetycznego

Kołowy przewodnik z prądem.

Wyznaczamy B dla punktów leżących na osi tego okręgu.

---