Politechnika Śląska

Wydział AEiI

Laboratorium

z Modelowania Cyfrowego

Matlab i Simulink

Grupa 4., sekcja 11.

Wioletta Bujak

Arkadiusz Mazur

1. Podstawowe operacje przy użyciu pakietu MATLAB

Przykłady wprowadzania macierzy:

Utworzenie macierzy jednostkowej o rozmiarach 8x8.

» A=eye(8)

A =

1 0 0 0 0 0 0 0

0 1 0 0 0 0 0 0

0 0 1 0 0 0 0 0

0 0 0 1 0 0 0 0

0 0 0 0 1 0 0 0

0 0 0 0 0 1 0 0

0 0 0 0 0 0 1 0

0 0 0 0 0 0 0 1

Utworzenie macierzy B powstałej przez pomnożenie przez trzy macierzy powstałej przez wycięcie z macierzy A wierszy od trzeciego do ósmego, oraz kolumn od trzeciej do ósmej.

» B=3*A(3:8,3:8)

B =

3 0 0 0 0 0

0 3 0 0 0 0

0 0 3 0 0 0

0 0 0 3 0 0

0 0 0 0 3 0

0 0 0 0 0 3

Utworzenie macierzy B o wymiarach 5x5 i losowych wartościach elementu o rozkładzie normalnym.

» B=randn(5)

B =

-0.1356 -0.7989 0.3967 1.1252 0.3180

-1.3493 -0.7652 0.7562 0.7286 -0.5112

-1.2704 0.8617 0.4005 -2.3775 -0.0020

0.9846 -0.0562 -1.3414 -0.2738 1.6065

-0.0449 0.5135 0.3750 -0.3229 0.8476

Rozwiązanie układu równań

Utworzenie macierzy B o wymiarach 5x1 i losowych wartościach elementu o rozkładzie naturalnym.

» B=randn(5,1)

B =

0.2681

-0.9235

-0.0705

0.1479

-0.5571

Utworzenie macierzy A o rozmiarach 5x5 i wartościach o rozkładzie równomiernym.

» A=rand(5,5)

A =

0.7361 0.3653 0.6515 0.4364 0.3593

0.3282 0.2470 0.0727 0.7665 0.1665

0.6326 0.9826 0.6316 0.4777 0.4865

0.7564 0.7227 0.8847 0.2378 0.8977

0.9910 0.7534 0.2727 0.2749 0.9092

Rozwiązanie układu równań AX=B.

» X=A\B

X =

0.6377

-0.0538

1.2906

-1.3105

-1.2541

Sprawdzenie dokładności obliczeń.

» Err=A*X-B

Err =

1.0e-015 *

0.0555

0

0.0833

0.0833

0.1110

Otrzymana przez nas dokładność wyniku jest bardzo dobra ( błąd rzędu 10-15 ).

Obliczanie wartości funkcji i tworzenie wykresów.

Przebieg przykładowej funkcji jednowymiarowej.

» x=0:200

» y=sin(x./6)+2*cos(x./20)

» plot(x,y)

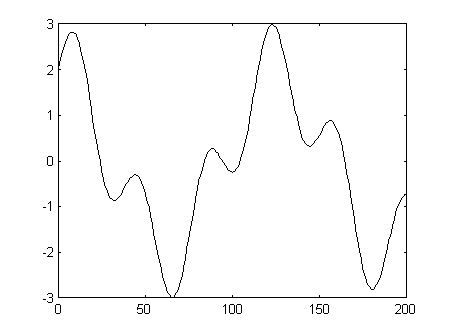
Przebieg przykładowej funkcji dwuwymiarowej.

» [X,Y]=meshgrid(-10:0.2:10,-10:.2:10)

» Z=sin(X-Y)*cos(X+Y)*x

» mesh(X,Y,Z)

2. Rozwiązanie zadania modelowego

Temat zadania

Wyznaczyć portret fazowy układu liniowego:

Czas całkowania t_max = 1000.

W celu rozwiązania zadania:

• zbudować model,

• opracować funkcję kreślenia pojedynczej trajektorii,

• opracować funkcję lub skrypt kreślenia portretu fazowego,

• wykreślić portret fazowy.

Model

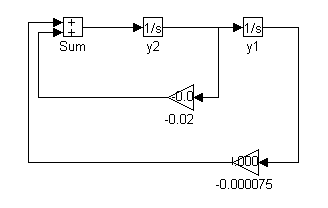
Na podstawie wyżej wymienionych równań stanu oraz korzystając z udostępnionych w pakiecie SIMULINK bloków operacyjnych zbudowaliśmy model badanego układu.

Pojedyncza trajektoria

Funkcja trajekt kreśli pojedynczą trajektorię portretu fazowego układu. Argumenty funkcji określają warunek początkowy. Do całkowania układu równań różniczkowych zastosowaliśmy metodę Rungego-Kutty 5 rzędu.

function trajekt(y10,y20)

[t,y]=rk45('cw2b',1000,[ y20; y10 ]);

plot(y(:,2),y(:,1));

Skrypt kreślenia portretu fazowego

Aby wykreślić portret fazowy modelu zastosowaliśmy wielokrotnie funkcję trajekt z różnymi wartościami warunków początkowych. Uzyskane trajektorie umieszczone zostały na jednym wykresie.

axis([-10 10 -0.05 0.05])

hold on

trajekt(10,0)

trajekt(-10,0)

for i=-9:9

trajekt(i,-0.05)

trajekt(i,0.05)

end

title('Portret fazowy')

xlabel('y1')

ylabel('y2')

hold off

Portret fazowy

Ponieważ pierwiastki równania charakterystycznego są rzeczywiste i mniejsze od zera, układ jest stabilny asymptotycznie.

Otrzymany przez nas portret fazowy jest portretem fazowym układu liniowego, w którym trajektorie dążą do punktu równowagi O(0,0) (węzeł stabilny) .

Na sporządzonym portrecie fazowym da się zauważyć dwa rodzaje asymptot. Jedna z nich to asymptota, do której zbiegają się trajektorie dla t dążącego do nieskończoności. Drugi rodzaj aymptot to te, które mają wspólny współczynnik kierunkowy dla wszystkich trajektorii.

Wnioski

W oparciu o środowisko MATLAB i pakiet SIMULINK można w prosty sposób przeprowadzić badania modelowe uzyskując przy tym bardzo dużą dokładność wyników. Umożliwia on także różnorodne sposoby prezentacji graficznej wyników poprzez bogaty zestaw funkcji generujących wykresy dwu- i trójwymiarowe. Pakiet SIMULINK wzbogaca środowisko MATLAB-a pozwalając na wizualne tworzenie modelu badanego układu, automatycznie generując plik źródłowy S-funkcji wykorzystywanej przy przeprowadzaniu badań modelowych.

MATLAB posiada bogaty zestaw operacji na macierzach, co w znaczny sposób upraszcza obliczenia. Po zapoznaniu się z oferowanymi przez środowisko operatorami można za pomocą jednego polecenia rozwiązywać układy równań.

---