6. CIĄG ZESPOŁU NAPĘDOWEGO

Ciąg wewnętrzny i ciąg efektywny silnika przepływowego

Siłą napędową samolotu odrzutowego jest ciąg silnika, który powstaje w wyniku wzajemnego oddziaływania ścian kanału przepływowego silnika i strumienia gazu przepływającego przez ten kanał oraz powietrza opływającego silnik z zewnątrz.

Przepływający przez silnik strumień powietrza (spalin) zwiększa swoją energię kinetyczną na skutek doprowadzonego do niego ciepła w komorze spalania silnika. Przyspieszenie strumienia jest możliwe dzięki odpowiedniemu ukształtowaniu ścian kanału przepływowego.

Oznacza to, że na strumień działa niezrównoważony układ sił od ścian kanału przepływowego. Zgodnie z prawem akcji i reakcji na ściany działają siły reakcji pochodzące od ciśnień wywieranych przez strumień.

Ciąg silnika odrzutowego (K) jest to składowa osiowa wypadkowej układu wszystkich sił działających na ścianki kanału przepływowego silnika i siły oporu powstającej w wyniku opływu zewnętrznego.

Rozróżnia się ciąg wewnętrzny K i ciąg efektywny K_e.

Ciąg wewnętrzny związany jest z procesami zachodzącymi wewnątrz silnika, nie uwzględnia sił działających na silnik (gondolę silnikową) w wyniku opływu strumieniem zewnętrznym. Inaczej mówiąc nie uwzględnia on oporu zewnętrznego działającego na napęd.

Ciąg efektywny jest częścią ciągu wewnętrznego, którą wykorzystuje się do pokonania sił oporu czołowego i sił bezwładności działających na samolot. Ciąg efektywny zapewnia ruch samolotu i jego przyspieszenia. Różnica między ciągiem wewnętrznym i ciągiem efektywnym równoważy opór zewnętrzny napędu.

W charakterystykach technicznych silników odrzutowych podaje się ciąg wewnętrzny, gdyż opór zewnętrzny zależy od miejsca zamontowania silnika oraz warunków lotu. Podczas pomiarów siły ciągu na hamowni, prędkość opływu strumieniem zewnętrznym równa jest zeru. W tych warunkach zerowa jest zatem siła oporu zewnętrznego i mierzony na hamowni ciąg jest ciągiem wewnętrznym.

Ciąg wewnętrzny silnika można obliczyć sumując składowe osiowe sił ciśnienia działających na wewnętrzne powierzchnie ścian kanału przepływowego. Ten sposób wyznaczenia ciągu nie ma jednak praktycznego zastosowania. Jakakolwiek zmiana zakresu pracy silnika lub zmiana parametrów strumienia wlotowego wymagałaby kolejnego, żmudnego obliczania i sumowania składowych osiowych pochodzących od ciśnień.

Znacznie prostszym sposobem jest wykorzystanie wzoru umożliwiającego obliczenie ciągu silnika którego wyprowadzenie opiera się na równaniu ilości ruchu masy (równaniu Eulera).

Model przepływu dla równania ciągu

Załóżmy, że silnik znajduje się w oddzielnej osiowosymetrycznej gondoli opływanej strumieniem z prędkością V, przy czym nie jest istotne czy prędkość V jest poddźwiękowa czy naddźwiękowa
(rys. 6.1).

Rys. 6.1 Model przepływu dla równania ciągu silnika przepływowego

Zgodnie z podanymi definicjami ciągu efektywnego i wewnętrznego możemy napisać:

(6.1)

Do wyznaczenia ciągu wewnętrznego K należy rozpatrzyć przyrost ilości ruchu strumienia powstający w objętości strumienia ograniczonej powierzchnią kontrolną pokazaną na rysunku 6.1. Powierzchnię kontrolną w tym przypadku stanowią:

• osiowosymetryczna, zewnętrzna powierzchnia swobodnego strumienia wlotowego H-1-2-wl

• powierzchnie ścianek kanału przepływowego silnika

• dwie powierzchnie prostopadłe do osi silnika H-H i 5-5 o polach powierzchni A_H i A₅

W przekroju H-H ciśnienie i temperatura powietrza są równe ich wartościom atmosferycznym p_H i T_H, a prędkości V równa jest prędkości lotu.

Równanie ciągu

Na strumień wydzielony powierzchnią kontrolną działają w kierunku osiowym następujące siły:

p_HA_H i p₅A₅ - siły oddziaływania odrzuconych części strumienia w przekrojach H-H i 5-5

- wypadkowa siła oddziaływania strumienia opływającego silnik na strumień
wlotowy miedzy przekrojami H-H i wl-wl

K' - wypadkowa siła oddziaływania ścian kanału przepływowego silnika na
strumień

Jeżeli jako kierunek dodatni przy sumowaniu sił przyjmiemy kierunek osi silnika o zwrocie zgodnym ze zwrotem wektora prędkości V lub c₅, to zgodnie z równaniem ilości ruchu suma wyszczególnionych sił (z uwzględnieniem znaku wynikającego ze zwrotu siły) będzie równa przyrostowi ilości ruch masy strumienia:

gdzie:

- strumienie masy, odpowiednio - spalin i powietrza.

Ciąg wewnętrzny K rozwijany przez silnik jest równy sile K' i ma przeciwny zwrot, a zatem:

(6.2)

Składowa osiowa wypadkowej siły działania strumienia na zewnętrzną powierzchnię gondoli może być wyrażona za pomocą zależności:

(6.3)

gdzie pierwszy człon odpowiada wypadkowej sił ciśnienia zewnętrznego działającego na powierzchnie gondoli, a drugi człon - sile tarcia zewnętrznego strumienia o powierzchnie gondoli.

Podstawiając wyrażenia (6.2) i (6.3) do (6.1) otrzymamy:

Dodajmy do prawej strony równania tożsamościową zależność:

Otrzymamy:

Po redukcji wyrazów o przeciwnych znakach, połączeniu dwóch pierwszych całek w jedna całkę o odpowiednio rozszerzonych granicach całkowania oraz zgrupowaniu wyrazów zawierających A₅ i wyłączeniu jej przed nawias dostaniemy:

Występujące w równaniu dwie całki można zapisać jako jedną całkę o tych samych granicach:

(6.4)

W celu uzyskania wzoru wyrażającego ciąg wewnętrzny, wystarczy założyć, że opływ zewnętrzny silnika przebiega bez oporów, bez tarcia, bez oddziaływania fal uderzeniowych itp., czyli w równaniu (6.4) można przyjąć, że p = p_H i X=0:

(6.5)

gdzie:

- strumień masy spalin

c₅ - prędkość wypływu strumienia z dyszy wylotowej

V - prędkość lotu

- strumień masy powietrza

- pole przekroju na wylocie z dyszy silnika

p₅ - ciśnienie strumienia w przekroju wylotowym dyszy

p_H - ciśnienie otoczenia

Strumień masy spalin różni się od strumienia masy powietrza o wartość sekundowego zużycia paliwa:

gdzie:

C_s - sekundowe zużycie paliwa

 - względne zużycie paliwa

(

Uwzględniając fakt, że wartość względnego zużycia paliwa w TSO z dopalaniem wynosi przeciętnie 0,03÷0,06 a w TSO bez dopalania 0,017÷0,023, co pozwala przyjąć:

Jeżeli ponadto zastąpimy prędkość lotu V równoważną prędkością strumienia c_H w przekroju H-H , to ostatecznie otrzymamy końcowy wzór na ciąg wewnętrzny przepływowego silnika odrzutowego:

(6.7)

Jeżeli
, co oznacza rozprężanie strumienia w dyszy do ciśnienia atmosferycznego, zależność przyjmie postać:

Przy pracy silnika w warunkach statycznych (V = c_H =0) i przy zupełnym rozprężaniu strumienia do ciśnienia otoczenia, ciąg silnika można wyrazić wzorem:

Ciąg napędu śmigłowego

Działanie różnych typów zespołów napędowych jest w ogólnym przypadku podobne, jakkolwiek napędy śmigłowe i śmigłowcowe wytwarzają ciąg w sposób pośredni, a napędy odrzutowe - w sposób bezpo­średni. Zadaniem silnika zaliczanego do pierwszej grupy jest dostarczanie mo­cy niezbędnej do napędu śmigła lub wirnika nośnego. Wytwarzanie ciągu w tym przypadku następuje przez zwiększenie prędkości zewnętrznego stru­mienia powietrza przepływającego przez płaszczyznę objętą ruchem obroto­wym śmigła lub wirnika nośnego. W drugiej grupie silników ciąg wytwarzany jest bezpośrednio jako skutek wzrostu prędkości przepływu mieszaniny po­wietrza i spalin w samym silniku. W obu przypadkach źródłem powstania siły ciągu jest przyrost ilości ruchu masy strumienia. W napędzie odrzutowym mała ilość strumienia masy ulega dużemu przys­pieszeniu, a w napędzie śmigłowym i śmigłowcowym - odpowiednio duża ilość strumienia masy podlega stosunkowo małemu przyspieszeniu.

Zadaniem śmigła, jako części zespołu napędowego samolotu, jest zamiana mo­mentu obrotowego silnika na siłę ciągu. Zasada pracy śmigła odpowiada trze­ciemu prawu Newtona: w czasie obrotu śmigło odrzuca z określoną siłą stru­mień powietrza do tyłu wzdłuż osi obrotu, a strumień z taką samą siłą odpycha śmigło (samolot) do przodu. Im większy jest strumień masy powietrza odrzucanego przez śmigło i większa prędkość odrzucanego strumienia, tym większy jest ciąg rozwijany przez śmigło.

W przypadku, gdy za pomocą śmigła energia mechaniczna silnika jest przek­ształcana na energię kinetyczną strumienia powietrza, to spełnia ono zadanie wentylatora. Gdy następuje przekształcenie energii poruszającego się strumienia powietrza na energię mechaniczną (moment obrotowy silnika), to śmigło speł­nia zadanie wiatraka.

Podstawowe parametry śmigła

W obliczeniach aerodynamicznych samolotu śmigło rozpatruje się wyłącznie jako wytwornicę ciągu przetwarzającą pracę silnika na pracę siły ciągu. Ozna­cza to, że od własności aerodynamicznych śmigła zależy, jaka część mocy prze­kazywanej przez silnik na wał śmigła zostanie zamieniona na moc użyteczną, określaną jako moc rozporządzalna zespołu napędowego. Stosunek mocy rozporządzalnej (użytecznej) śmigła do mocy silnika jest nazywany sprawnością śmigła.

(6.8)

gdzie:

P_r - moc rozporządzalna śmigła (zespołu napędowego)

P - moc silnika (moc na wale śmigła)

Sprawność obecnie eksploatowanych śmigieł osiąga wartość 0,80÷0,86.

Do podstawowych parametrów geometrycznych śmigła zalicza się jego średnicę D, kąt nastawienia elementu łopaty ϕ oraz posuw względny λ.

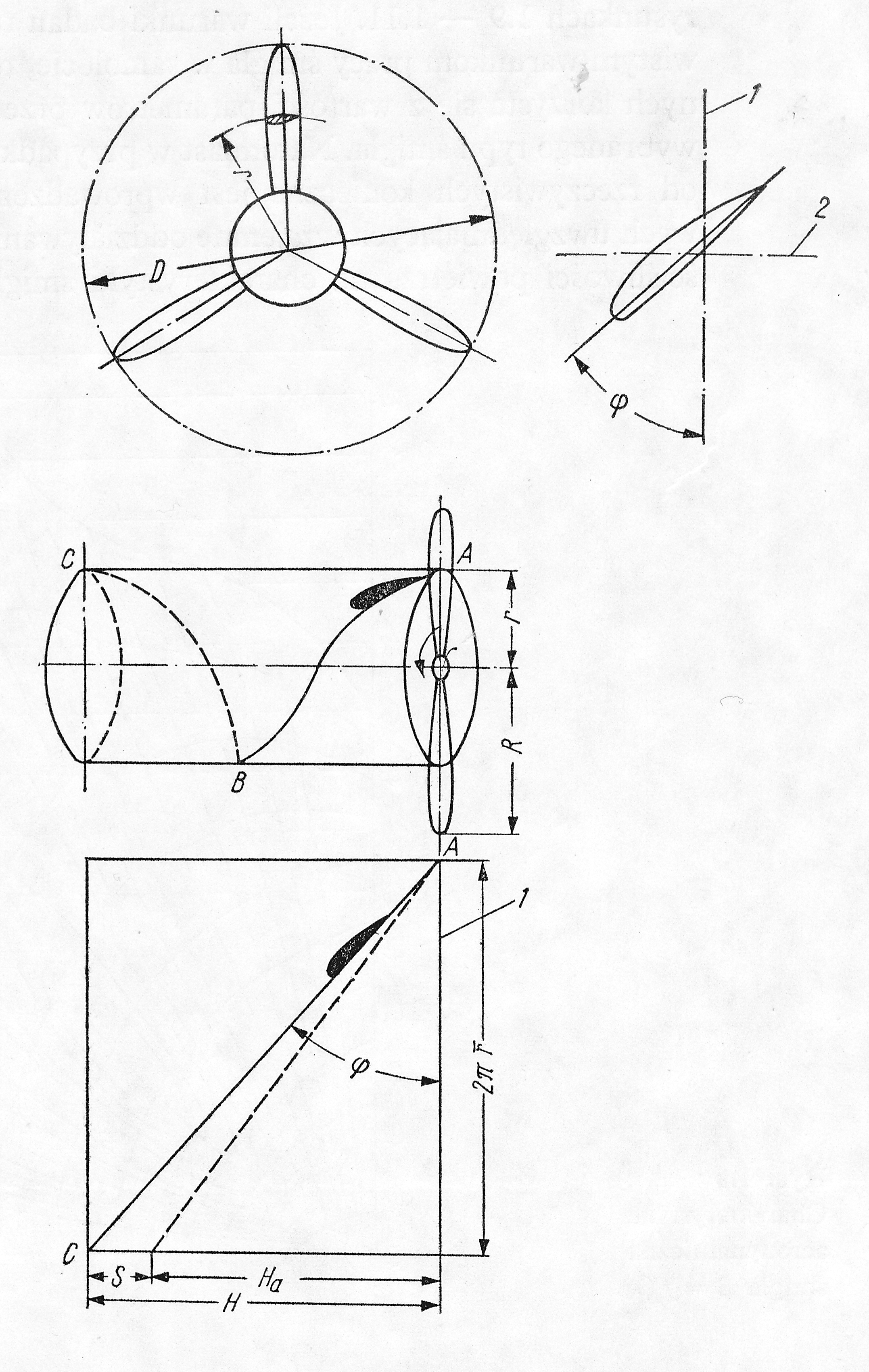
Rys. 6.2 Parametry geometryczne śmigła

1 - ślad płaszczyzny obrotu śmigła, 2 - oś obrotu śmigła

Średnicą śmigła D nazywa się średnicę okręgu opisywanego przez końce ło­pat w czasie obrotu śmigła. Przy założeniu stałej wartości innych parametrów od przyjętej wartości średnicy zależą: sprawność śmigła, dopuszczalna prędkość obrotowa, intensywność oddziaływania na charakterystyki aerodynamiczne samolotu itp. Przy doborze średnicy konieczne jest również uwzględnienie ogólnego układu samolotu i miejsca położenia silnika w płatowcu ze względu na jej wpływ, na przykład na wysokość podwozia i warunki pracy sąsiednich śmigieł.

Kątem nastawienia elementu łopaty ϕ nazywa się kąt utworzony przez cięciwę danego elementu łopaty i płaszczyznę obrotu śmigła. Kąt nastawienia ϕ całej łopaty określa się dla umownego elementu leżącego w odległości równej 75% pro­mienia łopaty śmigła licząc od osi obrotu śmigła.

Posuwem śmigła H_a nazywa się rzeczywistą odległość, jaką przebywa śmigło w czasie jednego obrotu w ośrodku podatnym, jakim jest powietrze. W locie, w czasie jednej sekundy śmigło przemieszcza się wzdłuż swojej osi na odległość równą prędkości lotu V oraz wykonuje n_s obrotów. Posuw rzeczywisty jest więc równy:

Posuw rzeczywisty jest różny od posuwu geometrycznego H, jaki miałby miejsce w czasie obrotu śmigła w ośrodku nieściśliwym, co przedstawiono na rysunku 6.2. W czasie lotu poziomego zachodzi zależność H_a < H, a w locie nurkowym H_a > H.

Przy określaniu charakterystyk śmigła zwykle posługuje się wartością posuwu względnego λ, tzn. posuwu rzeczywistego odniesionego do średnicy śmigła:

(6.9)

Posuw względny charakteryzuje zakres pracy śmigła i jest jednym z kryteriów podobieństwa modelu śmigła do konstrukcji rzeczywistej. Z tego względu charakterystyki śmigieł przedstawia się zwykle w postaci wykresów zależności współczynnika mocy lub współczynnika ciągu w funkcji posuwu względnego dla różnych kątów nastawienia łopat i sporządza na podstawie badań tunelowych śmigieł lub ich modeli (rys. 6.3).

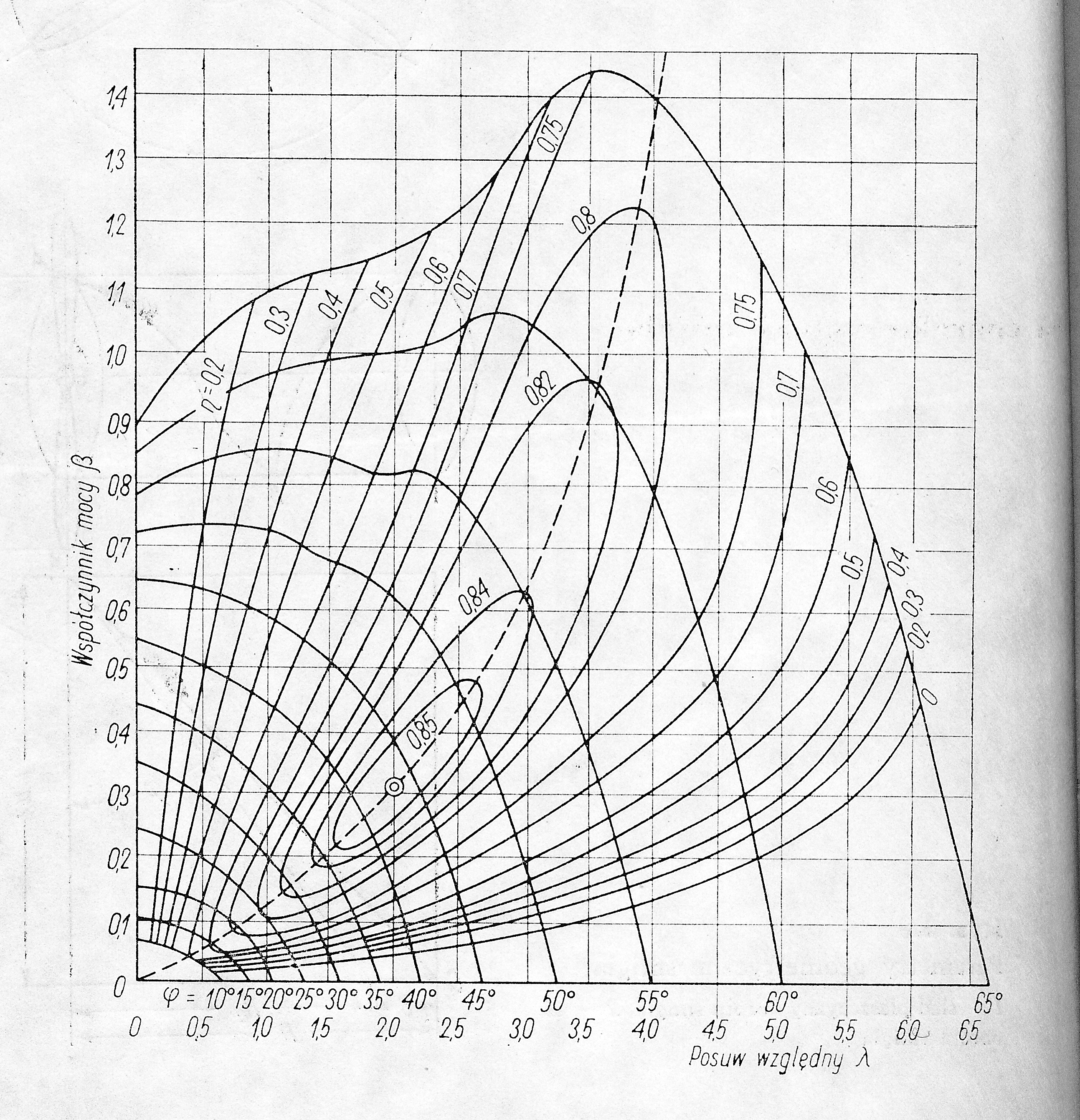
Rys. 6.3 Charakterystyka aerodynamiczna śmigła

1

A₅

K'

K

A_H

---