MRÓZ KRZYSZTOF

PROJEKT

NAPĘD ELEKTRYCZNY

PROJEKT 17

Dobrać silnik do napędu mechanizmu zmiany wysięgu dźwignicy jak na rys. i obliczyć czas rozruchu silnika do osiągnięcia przez silnik n=0.85 n
.

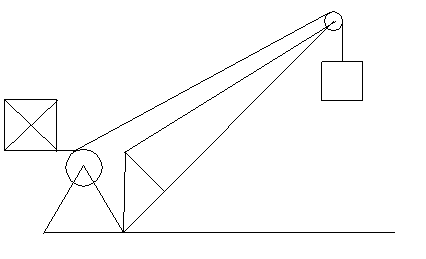
Silnik napędza bęben liniowy o średnicy D=0.53m , przez przekładnię i=15 o sprawności 0.89. Środek ciężkości

wysięgnika o masie m
=150 kg znajduje się w punkcie S. Masa m=1475 kg.

Wymiary:

a=1.75 m

l=2.5 m

L=7.23 m

Kąt w zakresie 0 do 70 stopni.

OBLICZENIA

F₁- siła w linie wyciągu od masy m

F₂- siła w linie wyciągu od masy m_w

M_b- moment na bębnie

M_s- moment na wale silnika

M_B=(F₁+F₂)*D/2

M_s=M_b/ηi=((F₁+F₂)D)/2ηi

-Równania momentów dla F₁

mgcosα=F₁r

2ϕ +α=120 2ϕ =120-α ϕ = (120-α)/2

cosϕ = r/a r = acosϕ = acos(60-α/2)

F₁=

-Równanie momentów dla F₂:

m_wglcosα = F₂r F₂=

M_s= M_b/ηi=((F₁+F₂)D)/2ηi=

α=70 M_s min

M_s min(70) = 463.5 Nm

α=0 M_s max

M_s max(0) = 2457 Nm

Po obliczeniu momentu max na silniku możemy określić jaką moc powinien osiągać ten silnik. Korzystamy ze wzoru :

M=9.55 P/n P=Mn/9.55

Po podstawieniu za n=750 obr/min wyliczamy że P=190 kW

Teraz z katalogu silników indukcyjnych dobieramy zadowalający nas silnik.

Tym silnikiem okazuje się SZDc 178d (8-biegunowy) o następujących parametrach , które osiąga przy n_s=750 obr/min.

P_N=200kW n_N=745 obr/min

I_SN przy 380V(500)-393A(298)

cosϕ=0.82 η=94.5 %

przeciążalność λ_N=M_Max/M=1.9

E₂₀=360A

I_WN=340A

R_W=0,005Ω

GD²[kGm²]=J_SIL 180

J_SPR=J_S+J_U/i²η_i

J_U=mD²/8=1475*0.53²/8=51.8[kGm²]

J_SPR=180/40+51.8*/(15²*0.89)=4.76[kGm²]

ω=2Π/60

Liczę teraz czas rozruchu:

M_N=9.55*P_N/n_N=2564[Nm]

M_R=1.6*M_N=4102[Nm]

M_M=M_K, M_M=1.9*M_N=4872[Nm]

n₂=633 obr/min

s₂=(n₂-n)/n₂

M_RŚR=0.9(M_R+M_K)/2=4038[Nm]

t_r=J_SPR*ω/(M_RŚR-M_m)=1.96 s(5.43 s)

Przewiduję rozruch ciężki :

I_2max=λ*I_2N

I_2max=1.8*I_2N

s_N=
=0,0067

m=
9,5

czyli m=9

I'_2MIN=I_2MAX( (I_MAX*s_N)/I_2N)^1/9 =1.9*I_2N
1,17*I_2N

I'_2MIN=1,17*I_2N=397,8A

ϑ-przekładnia prądowa silnika

ϑ=I_2N/I_1N=0,865

I'_1MIN= I'_2MIN*(1/ϑ)=459,81A

α'=
0,616

R_I=
0,322Ω

R_I =α'* R_I=0,198 Ω

R_III=α'* R_II=0, 122Ω

R_IV=α'* R_III=0,075 Ω

R_V=α'* R_IV=0, 0464Ω

R_VI=α'* R_V=0, 0,03Ω

R_VII=α'* R_VI=0, 0176Ω

R_VIII=α'* R_VII=0,011 Ω

R_IX=α'* R_VIII=0,0066 Ω

R_X=
+R_W

Po rozwiązaniu szeregu równań otrzymujemy:

R9=0,0011

R8=0,0049

R7=0,0066

R6=0,0174

R5=0,0114

R4=0,0286

R3=0,047

R2=0,076

R1=0,124

Prąd zwolnienia przekaźnika PI jest równy prądowi przełączenia silnika:

I_{Z PI}=I_1MIN i w naszym przypadku będzie równy 459,81A

1

4

---