Wydział Górniczy Wrocław dnia 2000-03-22

Ćwiczenie

Oznaczanie współczynnika filtracji

Wykonali: Wysocka Aneta

Rzepska Anna

Turkowski Rafał

Wysocki Marcin

Iwasiuk Marta

Pełka Radek

Januszkiewicz Janusz Michalski Robert

Maleszewski Krystian Zechman Krzysztof Tymrakiewicz Rafał

Rok akademicki 1999/2000

Wstęp teoretyczny.

Współczynnik filtracji jest bardzo istotnym elementem charakteryzującym badany grunt, pozwala on na określenie w sposób ilościowy i jakościowy rodzaju ruchu wód podziemnych.

Istnieje wiele metod pozwalających na określenie jego określenie z większym czy mniejszym przybliżeniem. To jaką metodę zastosuje się do jego określania zależy od wymaganej dokładności, czasochłonności danej metody i jej kosztów.

Najbardziej dokładne, uwzględniające niejednorodność ośrodka gruntowego, warunki lokalne, dające najdokładniejsze wyniki lecz jednocześnie najbardziej czasochłonne i kosztowne są badania polowe takie jak pomiar dopływu do studni (próbne pompowanie).

Badania laboratoryjne dają niestety tylko wartości przybliżone. Wykonywane są na próbkach o naruszonej strukturze nie uwzględniają niejednorodności gruntu oraz sposobu zalegania. Są jednak proste do wykonania, pozwalają na dość dokładne wstępne oszacowanie wartości współczynnika filtracji. Opierają się one na badaniu opracowanym przez francuskiego badacza H. Darcy, który dzięki swym doświadczeniom stworzył podstawy hydrauliki wód podziemnych, a polegające na badaniu przepływu wody przez cylinder wypełniony gruntem.

Oznaczanie współczynnika filtracji może być dokonywane metodą przepływu ustalonego, tzn. przy niezmiennych w czasie parametrach (spadek hydrauliczny, objętość wypływającej wody), np. za pomocą aparatu Wiłuna, lub metodą przepływu nieustalonego (przy zmiennej różnicy ciśnień) przy pomocy rurki Kamieńskiego, która dzięki swej prostej budowie nadaje się do badania zarówno w warunkach polowych jak i laboratoryjnych.

Współczynnik filtracji można również określić wykorzystując wzoru empiryczne stworzone dzięki badaniom przeprowadzonym jeszcze w ubiegłym wieku w U.S.A., które doprowadziły do stwierdzenia zależności filtracji od granulo - metrycznego składu gruntu, porowatości i temperatury wody.

Oznaczanie współczynnika filtracji metodą rurki Kamieńskiego.

Wstęp teoretyczny.

Przyrządem, który pozwala na łatwy i szybki pomiar współczynnika filtracji, także w warunkach terenowych, jest rurka Kamieńskiego. Przyrząd ten składa się z rury szklanej o średnicy
6 cm opatrzonej w skalę centymetrową. Jeden koniec rury obciągnięty jest gazą. Do rury wsypaliśmy próbkę piasku o wysokości 10,6 cm od dna rury. Po umieszczeniu próbki piasku nalewamy wody ponad zero podziałki. Oznaczenie współczynnika filtracji polega na pomiarze prędkości obniżania poziomu wody w rurce o 5 cm w czasie t.

Współczynnik filtracji obliczany jest ze wzoru:

gdzie:

k - współczynnik filtracji

l - wysokość próbki gruntu

t - czas w sekundach, w ciągu którego zwierciadło wody obniżyło się o wysokość s

s - wielkość obniżenia zwierciadła wody

h₀ - wysokość poziomu wody na początku pomiaru

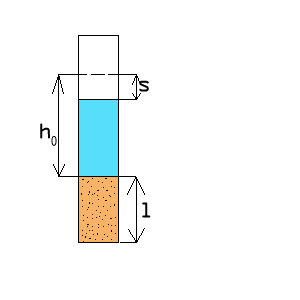
Badanie zostało przeprowadzone w aparaturze, której schemat został przedstawiony powyżej. Polegało ono na pomiarze czasu opadania wody w rurce pomiarowej pomiędzy poszczególnymi poziomami 45 cm, 50 cm i 55 cm. Dla każdego poziomu badanie zostało powtórzone trzykrotnie.

Wyniki pomiarów.

Średnica rury z próbą D=47 mm

Powierzchnia przekroju poprzecznego rury z próbką:

Obliczenia współczynnika filtracji:

1. Zakres 1-2

l = 10,6 cm

h₀ = 44 cm

t = 65 s

s = 5 cm

k₁ =

2. Zakres 2-3

t = 141 s

s = 10 cm

k₂ =

3. Zakres 3-4

t = 230 s

s = 15 cm

k₂ =

k_{a śr} =

4. Zakres 1-2

t = 71 s

s = 5 cm

k₄ =

5. Zakres 2-3

t = 155 s

s = 10 cm

k₅ =

6. Zakres 3-4

t = 271 s

s = 15 cm

k₆ =

k_{b śr} =

7. Zakres 1-2

t = 79 s

s = 5 cm

k₇ =

8. Zakres 2-3

t = 165 s

s = 10 cm

k₈ =

9. Zakres 3-4

t = 271 s

s = 15 cm

k₁ =

k_{c śr} =

Średnia wartość współczynnika filtracji:

Wnioski.

Największy wpływ na dokładność pomiarów miał odczyt czasu. Stąd bierze się wniosek, że można zwiększyć dokładność pomiarów współczynnika filtracji k poprzez wydłużenie czasu filtracji.

Analiza sitowa.

Wstęp teoretyczny.

Analizę sitową wykonywaliśmy wstrząsając wysuszoną próbkę gruntu

nr 1 przez zestaw sit o wymiarach boków oczek kwadratowych: 2,5 mm, 2 mm, 1,02 mm, 0,5 mm, 0,2 mm, 0,12 mm, 0,075 mm. Próbki gruntu po uprzednim zalaniu wodą i roztarciu w celu rozdzielenia zlepionych ziaren suszy się w temperaturze 105-110 ^oC do stałej masy. Następnie ważymy na wadze technicznej, z dokładnością do 0,01g, 0,5 kg próbki gruntu i wsypujemy do górnego sita, po czym przesiewamy za pomocą mechanicznego wstrząsania kompletu sit.

Wynikiem przesiewu jest rozdzielenie poszczególnych frakcji i zatrzymanie ich na kolejnych sitach. Na denku pozostają ziarna, których nie zatrzymało sito o mniejszej średnicy oczek (0,075 mm). Po przeniesieniu próbki z powrotem ważymy poszczególne frakcje pozostałe na sitach. Po zważeniu na wadze technicznej oblicza się zawartość procentową poszczególnej frakcji w próbce gruntu.

Suma mas poszczególnych frakcji powinna być równa masie wziętej do badania. Błąd dopuszczalny nie powinien przekroczyć 5%. Otrzymane wyniki nanosimy na wykres uziarnienia gruntu. Naniesione punkty łączymy otrzymując w ten sposób krzywą uziarnienia badanego gruntu.

Procentową zawartość poszczególnych frakcji obliczamy wg wzoru:

A = ( m_s ÷ m_c) ⋅ 100%

A - procentowa zawartość frakcji;

m_s - masa frakcji zatrzymanej na sicie;

m_c - masa całej próbki pobranej do badania.

Wyniki pomiarów.

Wartości odczytywane z wykresu uziarnienia gruntu:

d₆₀ = 1,3 mm

d₅₀ = 1,0 mm

d₁₀ = 0,2 mm

Współczynnik różnoziarnistości U:

U = d₆₀÷d₅₀ = 6,5

Na podstawie wzoru Hazena:

K₁₀ - współczynnik filtracji

K₁₀ = 1,16 ⋅

= 0,0464

Na podstawie wzoru Seelkeima:

K₁₀ = 0,357 ⋅

= 0,357

Wnioski.

Badana próbka gruntu ma prawie równomierne uziarnienie co można zobaczyć po kształcie krzywej uziarnienia. W obliczeniach wyszły nam różne współczynniki filtracji, różnica ta spowodowana jest obecnością w badanym gruncie ziaren o średnicy poniżej 0,1 mm. Różnice te spowodowane są niedokładnym sporządzaniem wykresu uziarnienia oraz mało dokładnym odczytaniem wartości.

Metoda przepływu ustalonego - aparat Wiłuna.

Schemat aparatu Wiłuna:

A - komora A

B - komora B

1. Próbka gruntu.

2. Pierścień, w którym umieszcza się badaną próbkę gruntu.

3. Perforowany krążek.

4. Obciążnik.

5. Podziałka

6. Dopływ wody do komory A.

7. Górny przelew.

8. Odpływ.

Wstęp teoretyczny.

Wyznaczanie współczynnika filtracji przy użyciu aparatu Z. Wiłuna polega na pomiarze ilości wody, która przesącza się w jednostce czasu przez próbkę gruntu przy stałej określonej wysokości i różnicy ciśnień. Aparat Wiłuna służy do badania przepuszczalności hydraulicznej piasków (od gruboziarnistych do pylastych) i żwirów. Główną część przyrządu tworzą dwa metalowe cylindry: zewnętrzny A i wewnętrzny B, które umożliwiają ustalenie różnych poziomów wody, oraz pierścień (2) w którym umieszcza się maksymalnie zagęszczoną próbkę badanego gruntu. Na dnie pierścienia umieszcza się siatkę filtracyjną. Pierścień z próbką umieszcza się w cylindrze wewnętrznym i przykręca się, tak aby ściśle przylegał do dna. Pierścień przykrywa się krążkiem (3), na którym następnie umieszcza się obciążnik (4) o masie 10 kg. Na ścianie komory wewnętrznej umieszcza się pionową podziałkę (5) i powoli napełnia się wodą, poprzez wlew (6) komorę zewnętrzną. Po osiągnięciu przez zwierciadło wody górnego przelewu (7) i gdy różnica ciśnień i wielkość wypływu wody ustali się, mierzymy ilość wody Q jaka wypłynie w określonym czasie z odpływu o stałej różnicy ciśnień Δh. W czasie badania dokonujemy pomiarów temperatury wody. Poszczególne pomiary, przy danym spadku hydraulicznym nie powinny się różnić więcej niż o 2%.

Wartość współczynnika filtracji oblicza się ze wzoru:

gdzie:

k_t - współczynnik filtracji w temperaturze t [^oC],

Q - objętość wody przepływającej przez daną próbkę [cm³],

F - przekrój próbki [cm²],

T - czas badania [s],

I - spadek hydrauliczny,

Δh - różnica wysokości.

l_p - wysokość próbki.

Wyniki pomiarów:

Wysokość próbki l₁ = 5,45 cm

l₂ = 5,45 cm l_śr = 5,45 cm

l₃ = 5,45 cm

Wysokość krążka l'₁ = 0,94 cm

l'₂ = 1,24 cm l'_śr = 1,08 cm

l'₃ = 1,06 cm

l_p = l_śr - l'_śr = 5,45 - 1,08 = 4,37 cm - wysokość próbki
Δl = 0,01 mm

Średnica próbki D₁ = 7,94 cm

D₂ = 7,98 cm D = 7,97 cm ΔD = 0,01 mm

D₃ = 8,00 cm

Temperatura wody T = 24 ^oC ΔT = 1 ^oC

Pole przekroju próbki F
49,89 cm2 ΔF = 0,5 cm2

Lp.	Q [cm^3 ]	h [cm]	h [cm]	h [cm]	Lp [cm]	I	F [cm^2 ]	k [cm/s]
1	127	4,5	1,2	3,3	4,37	0,7551	49,89	0,7714
2	133	4,9	1,2	3,7	4,37	0,8467	49,89	0,7205
3	127	4,4	1,2	3,2	4,37	0,7323	49,89	0,7955
4	127	4,4	1,2	3,2	4,37	0,7323	49,89	0,7955

ΔQ = 1 cm³

ΔI = 0,13

ΔT = 1 s

Średnia wartość współczynnika filtracji k_t = 0,77
Δk_t = 0,7

Wnioski.

Aby zwiększyć dokładność pomiarów należy utrzymywać spadek hydrauliczny na poziomie 0,3 - 0,8. Jak widać z danych w tabeli przekroczenie tych wartości powoduje duże rozbieżności wyników.

Grunt luźny na skutek nawodnienia podczas badania zagęścił się, zmieniając pierwotną wysokość próbki i jej porowatość. W celu uniknięcia błędu pomiarowego wysokość próbki mierzy się dla gruntu w stanie suchym.

Wartość spadku hydraulicznego jest opatrzona dużym błędem pomiarowym, gdyż pomiary wartości potrzebne do jej obliczenia dokonywane była za pomocą linijki o małej dokładności.

1

11

---