ATH WNoMiŚ
kierunek: budownictwo
Łukasz Skura i Mariusz Domański
Grupa I

Ćwiczenie nr 76

Wyznaczanie ogniskowej soczewki

I układu soczewek metodą Bessela

1. Wstęp teoretyczny

Soczewka to przezroczysta bryła ograniczona dwiema powierzchniami kulistymi lub jedną kulistą i jedną płaską. Ogniskiem soczewki skupiającej nazywamy punkt leżący na głównej osi optycznej (Rys.1) w którym zostaje skupiona po przejściu przez soczewkę wiązka promieni biegnących równolegle do osi optycznej w niedużej od niej odległości (tzw. promienie przyosiowe).

Rys. 1

Ogniskiem soczewki rozpraszającej nazywamy punkt leżący na głównej osi optycznej w którym przecinają sie przedłużenia (Rys.2) rozproszonych przez soczewkę promieni przyosiowych biegnących początkowo równolegle do głównej osi optycznej.

Rys. 2

Ogniskowa soczewki cienkiej (której grubość jest znacznie mniejsza od promieni krzywizny powierzchni zewnętrznych soczewki) jest równa odległości ogniska od środka soczewki. Ogniskowa soczewki rozpraszającej przyjmujemy umownie za ujemna.

Ogniskiem głównym soczewki nazywamy punkt, w którym przecinają się po przejściu przez soczewkę promienie równoległe do jej głównej osi optycznej. Ogniskową soczewki nazywamy odległość ogniska głównego soczewki od środka optycznego soczewki. Odwrotność ogniskowej nazywamy zdolnością zbierającą soczewki.

Ława optyczna (Rys.3):

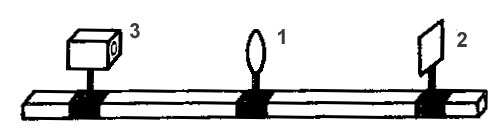
Rys. 3

1. Soczewka lub układ soczewek 2. Ekran 3. Przedmiot świecący

Metoda Bessela - przy stałej odległości przedmiotu od ekranu istnieją dwa położenia soczewki , przy których powstanie ostry obraz przedmiotu.

Oznaczając odległość przedmiotu (punktu) od jego obrazu (AA') przez d oraz odległość między dwoma położeniami soczewki (K i L), przy których obraz powstaje w tym samym miejscu, przez l , można napisać następujące zależności:

d = x + y ; l = y - x .

Rozwiązanie powyższych równań względem x i y ma postać:

;

Wstawiając x i y do równania soczewki:

Otrzymamy:

Wzór ten pozwala na wyznaczenie ogniskowej soczewki za pośrednictwem pomiaru odległości d i l. Warunek:
> 4f
i
.

Opisanej powyżej metody Bessela nie można zastosować bezpośrednio dla soczewki rozpraszającej ponieważ_ nie tworzy ona obrazu rzeczywistego przedmiotu. Aby pokonać tą trudność, wykorzystujemy układ soczewek składający sie z soczewki rozpraszającej oraz z soczewki skupiającej, której ogniskowa właśnie wyznaczyliśmy. Jest to układ skupiający, który może tworzyć rzeczywiste obrazy przedmiotu świecącego. Możemy zatem wyznaczyć

ogniskowa fu tego układu w taki sam sposób jak to wcześniej zrobiliśmy dla pojedynczej soczewki skupiającej. Wiadomo, że ogniskowa fu układu blisko siebie położonych soczewek jest powiązana z ich ogniskowymi fs i fr następującą zależnością:

gdzie : fs - ogniskowa soczewki skupiającej, fr - ogniskowa soczewki rozpraszającej.

2. Przebieg ćwiczenia

Celem pierwszej części ćwiczenia jest ustalenie z jakim błędem bezwzględnym jesteśmy w stanie wyznaczyć współrzędną soczewki na ławie optycznej, przy której na ekranie otrzymujemy ostry obraz przedmiotu. Następnie dokonujemy pomiaru ogniskowej.

Na ławie optycznej (Rys.3) umieściliśmy świecący przedmiot, ekran oraz soczewkę skupiającą. Przedmiot powinien znajdować sie pobliżu początku skali natomiast ekran ustawić w odległości 80 cm od początku skali ławy optycznej. Przesuwając soczewkę wzdłuż ławy optycznej staraliśmy się otrzymać na ekranie ostry obraz przedmiotu. Czynność powtarzamy czterokrotnie, za każdym razem przesuwając soczewkę poza „ostre” położenie. Wyniki notujemy w tabeli 1 - współrzędna a1. Znajdujemy takie położenie soczewki, przy którym na ekranie powstanie ostry, pomniejszony obraz. Czynność powtarzamy czterokrotnie, za każdym razem przesuwając soczewkę poza „ostre” położenie. Wyniki notujemy w tabeli 1 jako współrzędne a2.

Tab. 1 Obliczanie błędu bezwzględnego współrzędnych a1 i a2

a1 [cm]	<a1> [cm]	Sa1 [cm]	∆a1 [cm]	a2 [cm]	< a2> [cm]	Sa2 [cm]	∆ a2 [cm]
19.0	18.98	0.18	0.20	71.5	71.44	0.071	0.12
18.9										71.4
18.8										71.4
19.2										71.4
19.0										71.5

Umieszczamy ekran przy współrzędnej xE = 100 cm, nie zmieniając położenia przedmiotu święcącego. Znajdujemy takie położenia soczewki, przy których na ekranie powstają kolejno ostre obrazy: powiększony i pomniejszony przedmiotu świecącego. Odczytane współrzędne a1 i a2 wpisujemy do tabeli 2. Czynność powtarzamy przy współrzędnej xE =90 cm, 80 cm, 70 cm i 60 cm, przy nie zmienionym położeniu przedmiotu świecącego. Współrzędne soczewek a1 i a2 dające ostre obrazy wpisujemy do tabeli 2.

Tab.2. Wyniki pomiarów dla soczewki skupiającej

xP [cm]	xE [cm]	a1 [cm]	a1 [cm]	a2 [cm]	a2 [cm]	d [cm]	d [cm]	l [cm]	l [cm]	f1i [cm]	f1 [cm]	f1i [cm]	f1 [cm]
10	100	18.5	0.2	93.5	0.12	75	0.32	90	0.1	6.87	7.46	0.1	0.7
10	90	18.8				81.5				62.7				80		7.71		0.2
10	80	18.8				71.5				52.7				70		7.58		0.1
10	70	19.1				61.3				42.2				60		7.58		0.1
10	60	19.6				51				31.4				50		7.57		0.2

Następnie powtarzamy czynności pomiarowe zastępując soczewkę skupiającą

układem soczewek. Tym razem ekran umieszczamy kolejno przy współrzędnej xE = 145cm, 140 cm, 135 cm , 130 cm i 125cm, nie zmieniając położenia przedmiotu świecącego. Wyznaczone dla każdego z tych przypadków współrzędne układu soczewek a1 i a2zapewniające ostre obrazy przedmiotu wpisujemy do tabeli 3.

Tab.3. Wyniki pomiarów dla układu soczewek

xP [cm]	xE [cm]	a1 [cm]	a1 [cm]	a2 [cm]	a2 [cm]	d [cm]	d [cm]	l [cm]	l [cm]	f1i [cm]	f1 [cm]	f1i [cm]	f1 [cm]
10	145	48.8	0.2	110	0.12	61.2	0.32	135	0.05	26.83	26.39	0.04	0.11
10	140	47.5				105				57.5				130		26.14		0.01
10	135	48.8				100.5				52.2				125		25.80		0.02
10	130	52				91				39				120		26.83		0.01
10	120	52.5				85.5				33				115		26.38		0.02

3. Opracowywanie wyników

Obliczamy błędy bezwzględne ∆a1 i ∆ a2, jakimi są obarczone wartości współrzędnych a1 i a2. Obliczamy średnią arytmetyczną z pięciu pomiarów współrzędnej a1 i wpisujemy do tabeli 1.

>

Obliczamy średni błąd kwadratowy pojedynczego pomiaru skorygowany

współczynnikiem Studenta tα,n:

Współczynnik Studenta tα,n odczytujemy z tablic, przyjmując poziom ufności α=0.7 i liczbę pomiarów n=5.

Błąd bezwzględny współrzędnej a1 obliczamy według wzoru:

gdzie - błąd systematyczny odczytu współrzędnej równy 0.1cm.

Powtarzamy wszystkie obliczenia dla współrzędnej a2, wyniki zapisujemy w odpowiednich kolumnach.

Na podstawie współrzędnych soczewek (a1 i a2), ekranu (xE) i przedmiotu (xP)

zgromadzonych w tabelach 2 i 3, obliczyć dla kadiego przypadku następujące odległości: d = a2 - a1, l = xE - xP oraz ogniskowa f, korzystając z równania. Rezultaty obliczeń wpisujemy do tabel 2 i 3. Obliczamy obliczyć bledy bezwzględne d i l :

 d  
∆ a2

 l   xE
∆ xP

Przyjmujemy błąd odczytu współrzędnych xE = xP = 0.1 cm, wyniki zamieściliśmy w tabelach 2 i 3.

Na podstawie danych zgromadzonych w tabelach 2 i 3 obliczyliśmy i wpisaliśmy do tabel 2 i 3 błędy bezwzględne ogniskowych soczewki skupiającej i układu soczewek dla każdego wykonanego pomiaru, korzystając z zależności:

Obliczyliśmy i wpisaliśmy do tabel 2 i 3 wartości średnie ogniskowych f1 i fu oraz ich błędy bezwzględne f1 i fu , korzystając z zależności:

Obliczamy ogniskowa f2 soczewki rozpraszającej, korzystając z wyliczonych w poprzednim punkcie średnich wartości ogniskowych f1 i fu, po przekształceniu wzoru:

Obliczamy błąd bezwzględny soczewki rozpraszającej:

(

4. Wnioski

Wykonanie ćwiczenia potwierdziło nasze przypuszczenia - mianowicie, że ogniskowa układu soczewek jest większa niż ogniskowa każdej z soczewek osobno, czyli łącząc soczewki w układ możemy uzyskać lepsze własności optyczne.

2

---