Temat: Pomiary dyfrakcyjno-interferencyyjne światła laserowego.

Pomiar średnicy bardzo małych okrągłych otworów przy wykorzystaniu

dyfrakcji światła.

Zasada działania i własności światła lasera.

Istota działania lasera polega na wykorzystaniu zjawiska promieniowania wymuszonego. Promieniowanie takie przewidział teoretycznie A.Einstein już w 1917 r. Dopiero jednak w roku 1960 zbudowano dwa pierwsze lasery. T.H. Maiman był twórcą lasera rubinowego, a pod

kierunkiem A. Javana powstał laser gazowy He - Ne. Słowo laser pochodzi od pierwszych liter angielskiej nazwy: Light Amplification by Stimulated Emission of Radiation (wzmocnienie światła przez wymuszoną emisję promieniowania).

A. Einstein udowodnił, że promieniowanie wymuszone powinno mieć własności identyczne z własnościami promieniowania przechodzącego przez substancję i wywołującego promieniowanie wymuszone. Powstające w wyniku przejścia atomów (lub cząsteczek) na niższe

poziomy energetyczne pod wpływem światła, fotony mają tę samą energię(częstość), poruszają się dokładnie w tym samym kierunku, są identycznie spolaryzowane i drgają w zgodnej fazie (są spójne) co fotony wymuszające je. A więc zjawisko promieniowania wymuszonego polega na zwiększeniu

amplitudy fali przechodzącej przez substancję nie powodując zmiany jej częstości, kierunku rozchodzenia, fazy i polaryzacji. Jest ono spójne z promieniowaniem wymuszającym.

Dla zrozumienia zasady działania lasera wystarczy przyjąć, że materia jest pewnym makroukładem, złożonym z olbrzymiej liczby mikroukładów (atomów, cząsteczek), a promieniowanie traktować w sensie kwantowym jako zbiór fotonów.

Każdy mikroukład może znajdować się w różnych stanach kwantowych określonych dyskretnymi wartościami energii związanymi z położeniami elektronów na odpowiedniej orbicie. Stan o najniższej

energii nazywa się stanem podstawowym, pozostałe nazywa się stanami wzbudzonymi. Jeżeli atom znajduje się w jakimś stanie o energii W ', to może on przejść do stanu energetycznie wyższego W", jeżeli uzyska kwant energii równy: W=W"-W `=hv" ' ,

gdzie:

v" `, - częstość fali elektromagnetycznej związanej z fotonem,

h - stała Plancka.

Absorpcja fotonu ma tu charakter rezonansowy. Gdyby częstość padającego promieniowania nie spełniała w/w zależności, wówczas przejścia między poziomami W `, i W" i akty absorpcji nie byłyby możliwe (dokładniej byłyby mało prawdopodobne). Naturalnym zachowaniem się atomu wzbudzonego jest przechodzenie do stanów energetycznie niższych i wysyłanie promieniowania spontanicznego o częstości równej v" `. Kierunek, faza i polaryzacja fali wypromieniowanej są przypadkowe. Przejście do niższego stanu energetycznego może być i bezpromieniste, np. na skutek zderzenia się atomów, oddany wtedy kwant energii zwiększa energię cieplną ośrodka.

Gdyby wydzielono atom z makroukładu, wówczas po pewnym czasie znalazłby się on w stanie podstawowym. Ponieważ atom ten nie jest sam, to obok przejścia do niższych poziomów mogą istnieć przejścia na poziomy wyższe związane z pobraniem. energii od innego atomu na

skutek zderzenia lub pochłonięcia fotonu. Energia wewnętrzna zamkniętego makroukładu jest stała i w danej chwili jest w określony sposób rozłożona między poszczególne atomy.

Ponieważ nie interesuje nas konkretny atom, ale zachowanie się zbioru atomów, ponadto ponieważ zbiór jest bardzo liczny i akty przekazywania energii są przypadkowe, to na podstawie praw statystyki matematycznej można wyznaczyć rozkład atomów znajdujących się w poszczególnych stanach energetycznych. Oczywiście istnieją zawsze przejścia atomów z

jednego stanu do drugiego, ale w stanie równowagi termicznej średnia liczba atomów przechodzących w jedną stronę jest równa średniej liczbie atomów przechodzących w przeciwnym kierunku. Oznacza to, że obsadzenia poziomów w danym makroukładzie są stałe w czasie.

Budowa lasera He - Ne.

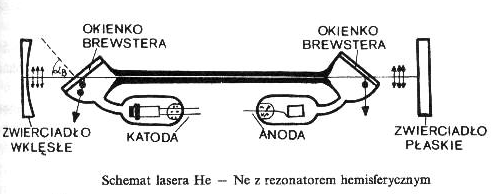
Laser helowo-neonowy należy do najczęściej stosowanych laserów w laboratoriach i pracach naukowych. Widmo absorpcyjne i emisyjne neonu jest liniowe, dzięki słabemu oddziaływaniu między atomami (małe ciśnienie) ośrodka. Inwersja obsadzeń stanów energetycznych przez elektrony ("pompowanie optyczne") odbywa się dzięki wyładowaniu elektrycznemu w mieszaninie helu i neonu. W laserze, który jest wykorzystany w niniejszym ćwiczeniu ciśnienie całkowite gazów wynosi około 2 Tr, a na jedną objętość neonu przypada około 8 objętości helu. Wąskie pasma (energetyczne) emisyjne dają generację lasera tylko na modach (częstościach) podłużnych. Przy zastosowaniu wielowarstwowych zwierciadeł dielektrycznych można doprowadzić do generacji jednoczęstotliwościowej.

Pierwszy laser helowo-neonowy, który powstał w 1961 r. generował promieniowanie o długości

1,15 m. W następnym roku odkryto generację lasera He - Ne o długości fali  = 0,6328 m. Mimo upływu czasu laser ten niepodzielnie panuje na rynku laserów niskiej mocy.

Głównymi elementami tego lasera są: rura wyładowcza, rezonator optyczny (złożony z dwóch zwierciadeł) i zasilacz. Rura wyładowcza wykonana jest w postaci kapilary o długości np. 600 mm i średnicy wewnętrznej 2 mm ze szkła laboratoryjnego. W skład zespołu rury wyładowczej wchodzą bańka katodowa i anodowa, które stanowią osłony dla elektrod rury wyładowczej. Katoda wykonana jest w postaci cylindra z blachy aluminiowej. Anoda jest wolframowa. Rura wyładowcza zamocowana jest na wspornikach. Kapilarę na końcach zamykają dwa okienka szklane ustawione pod kątem Brewstera  . Rura wyładowcza znajduje się między zwierciadłami rezonatora optycznego w układzie hemisferycznym. Odległość między zwierciadłami wynosi około 700 mm. Jedno zwierciadło jest sferyczne wklęsłe o promieniu krzywizny 2m i odbija w całości promieniowanie. Drugie zwierciadło jest płaskie i przepuszcza 1,5% promieniowania. Rura wyładowcza i rezonator umieszczone są w obudowie metalowej. Odpowiednie ustawienie zwierciadeł (prostopadłe do

osirury kapilarnej) umożliwiają po dwie z każdego końca obudowy mikrośruby.

Źródłem energii jest zasilacz, który dostarcza prąd o natężeniu około 10 mA przy napięciu około

1,7 kV. Układ zasilacza zaopatrzony jest w automatyczne urządzenie samozapłonowe. Automatyczny zapłon następuje po trzech sekundach od chwili włączenia zasilacza, a jego napięcie szczytowe wynosi około 8 kV.

W laserze tym do generacji promieniowania są wykorzystywane przejścia między poziomami energetycznymi neonu, a hel jest gazem buforowym niezbędnym przy pompowaniu elektrycznym. Najpierw na skutek zderzeń z elektronami wzbudza się hel, a następnie sam zderzając się z atomami neonu powoduje jego wzbudzenie.

Na rys .przedstawiono poziomy energetyczne helu i neonu biorące udział w akcji laserowej. Dla przejrzystości rysunku odległości między poziomami energetycznymi są orientacyjne. Oznaczenia poziomów są zgodne z symboliką stosowaną w spektroskopii. Każdy z poziomów neonu ma wiele podpoziomów, dlatego przejścia między różnymi podpoziomami dwóch poziomów pozwalają uzyskać generację promieniowania o różnych długościach fal. Najłatwiej uzyskać generację, a także otrzymać największą moc promieniowania lasera He - Ne dla fal o długościach:  = 0,6328 m ,  = 1,153 m i  = 3,3913 m.

W przypadku, gdy zwierciadła rezonatora znajdują się poza kapilarą, wtedy jest ona zamknięta płytkami płasko-równoległymi ustawionymi pod kątem Brewstera do osi rezonatora. Dzięki temu składowa natężenia wektora świetlnego leżąca w płaszczyźnie padania przechodzi przez płytki prawie bez strat, dla składowej prostopadłej do płaszczyzny padania, straty dla przejścia w jednym kierunku przekraczają 30 %.

Dlatego warunek generacji jest spełniony tylko dla jednej składowej, leżącej w płaszczyźnie padania i promieniowanie lasera jest spolaryzowane liniowo.

Czas życia lasera jest określony zwykle przez spadek mocy wyjściowej do połowy jej wartości początkowej. Na spadek mocy ma wpływ zanieczyszczenie gazów, ucieczka helu z kapilary i związana z tym

zmiana proporcji między cząstkowymi ciśnieniami helu i neonu, zanieczyszczenie okienek rozpylonym aluminium oraz spadek jakości zwierciadeł. Czas życia obecnie produkowanych laserów He - Ne wynosi około 20 tys.godzin. Sprawność tego lasera wynosi około 0,1 %. Obecnie obok laserów He - Ne należących do grupy laserów atomowych, produkowane są lasery krystaliczne

(np. rubinowe), gdzie ośrodkiem czynnym jest ciało stałe, a także gazowe - jonowe, molekularne

(np. CO2), półprzewodnikowe, cieczowe, barwnikowe, chemiczne i inne.

Światło laserowe wyróżnia od światła ze źródeł klasycznych:

1. Bardzo mała rozbieżność wiązki (kierunkowość). Kąt między

skrajnymi promieniami wiązki laserowej jest rzędu miliradiana.

2. Duże natężenie światła w wiązce.

3. Dużo większa monochromatyczność.

4. Wysoki stopień spójności. Pod pojąciem spójności promieniowania rozumiemy korelację między fazami drgań w różnych punktach przestrzeni w tym samym czasie (spójność przestrzenna) albo między fazami.

drgań w jednym i tym samym punkcie, ale w różnych momentach czasu (spójność czasowa).

5. Światło laserowe może być całkowicie spolaryzowane.

6. Wartość natężenia wektora elektrycznego w wiązce laserowej osiąga wartość 10000000 V/cm . Podczas, gdy dla światła słonecznego wynosi zaledwie 7 V /cm.

Dyfrakcja płaskiej fali świetlnej na bardzo małym okrągłym otworze (dyfrakcja Fraunhofera).

O ile rozkład energii w widmie dyfrakcyjnym nieskończenie długiej szczeliny można było opisać przy pomocy wzorów względnie łatwo, to dla otworu okrągłego zagadnienie staje się trudniejsze. Wychodzi się z całki opisującej dyfrakcję Fraunhofera i po wykorzystaniu współrzędnych biegunowych otrzymujemy na rozkład natężenia w obrazie dyfrakcyjnym wzór:

gdzie: J1(x) - oznacza funkcję Bessela pierwszego rodzaju i pierwszego rzędu zmiennej x, wyrażonej wzorem:

gdzie poszczególne wielkości są zgodne z oznaczeniami na rys.

- dlugość fali promieniowania

p - promień otworu w zasłonie Z,

OP - odległość od środka obrazu dyfrakcyjnego 0 do punktu obserwacji P na ekranie E,

r - odległość od środka O' otworu w zasłonie do punktu obserwacji P(r~d).

Obraz dyfrakcyjny otrzymany dla bardzo małego okrągłego otworu (p - rzędu dziesiątych części milimetra),

składa się z jasnego krążka (Airy) i otaczających go na przemian pierścieni ciemnych i jasnych. Przy czym na krążek Airy'ego przypada 84 % całkowitej energii przechodzącej przez otwór w zasłonie Z.

Możemy określić promień p otworu, na którym następuje dyfrakcja.

Gdy zmierzymy, np. promień OP pierwszego jasnego pierścienia na ekranie E, to z w/w wzoru otrzymujemy:

Przy czym na wartość r można przyjąć z dobrym przybliżeniem

Odległość d między zasłoną z otworem Z a ekranem E.

Wyniki pomiarów:

Otwór nr :	I rząd OP[mm]	II rząd OP[mm]	III rząd OP[mm]	ρ mm]	S [mm]
3		4	7	0,40	0,80
1	4	5,5	----	0,249	0,499
6	6,5	11		0,15	0,30
8	8,5	13,5		0,117	0,235

r=1,93 m , odl. ekranu od otworu,

, m dł. fali światła laserowego

Ocena błędu pomiarów:

OP = 0,5 mm

r =1mm

dla otworu nr 3:

dla otworu nr 6:

Wnioski:

Z przeprowadzonych obserwacji wynika, że przy wykorzystaniu dyfrakcji światła lasera,

można, dokonywać pomiarów promieni czy średnic, bardzo małych otworów.

Przy czym pomiary te obdarzone są bardzo małym błędem.

---