Imię i nazwisko:	Ćw. O6 Dyfrakcja światła laserowego.
Kierunek i rok: .	Ocena z kolokwium: ………………….. …………………... Data/podpis	Ocena ze sprawozdania: …………………... …………………... Data/podpis	Ocena końcowa: …………………... …………………... Data/podpis
Nazwisko prowadzącego zajęcia:

Cel doświadczenia.

Wyznaczenie szerokości szczeliny prostokątnej i kołowej metodą dyfrakcji światła laserowego.

Przebieg doświadczenia:

1. Zamocować w uchwycie pojędzyńczą szczeline, włączyć laser na ekranie obserwować prążki interferencyjne.Śrubą mikrometryczną zmieniamy tak położenie aby szczelina znalazła się na środku miejśca w którm fale wygłuszyły się. Na bębnie śruby odczytujemy położenia dla 1-szego lub 2-go rzędu.

2. Zamontować w uchwycie przesłonę z otworem kołowym i zanotowć położenia prążków ciemnych pierwszego rzędu.

Teoria:

Interferencja pologe na nałożeniu się fal co prowadzi do wygłuszenia lub wzmocnienia fali. W wyniku tego powstaje obraz inteferencyjny w postaci jasnych i ciemnych prążków.

Doświadczenia Younga.

L- źródł światła.

Sz- szczelina w pierwszej przesłonie.

Sz1 i Sz2- szczelinana drugiej przeesłonie.

E- ekran.

d- oległość miedzy Sz1 i Sz2.

D- odległość miedzy szczelinami a ekranem.

l- odległość miedzy poszczegulnymi prążkami.

Szczelina Sz1 i Sz2 są oświetlone światłem z szczeliny Sz. Za Szelinami Sz1 i Sz2 fale za soba inteferują i widać na ekranie ciemny i jasne prążki czyli tak zwane minima i maksima inteferencyjne. Srodkowy prążek jest najwiekszy i najjaśniejsży ponieważ powstaje z fal nie ugietych czyli ma zerową amplitude.

Dyfrakcja światła polega na odchyleniu kierunku rożchodzenia światła od kierunku pierwotnego, jeśli natrafi na jakieś przeszkody. Innymi słowy mówiąc jest to ugięcie światła.

Dyfrakcja światła na pojędyńczej szczelinie.

b- szerokość szczeliny

h odległośc od ekranu

d- odległośc między poszczegulnymi prążkami.

Według zasady Huygensa każdy punkt, do którego dobiegła fala, może być potraktowana jako źródło naowej fali kulistej o częstości równej częstości fali padającej. Ponad to według younga dla bardzo małych kontów α

Dlatego warunek dla wygłuszenia fali można zapisać w postaci.

Dyfrakcja na otworze kołowym

Płaska monochromatyczna fala świetlna pada na otwór prostopadle do jego powierzchni.

Obraz dyfrakcyjny obserwujemy na ekranie w postaci jasnego krążka w współśrodkowych nim wystepujących przemiennia pierścieni ciemnych i jasnych. Kąt ugięcia odpowiadający pierwsemu ciemnemu pierścieniowi, ograniczającemu maksyma centralne spełnia warunek:

D- średnica otworu.

λ- dł. Fali świetlnej.

Laser He-Ne.

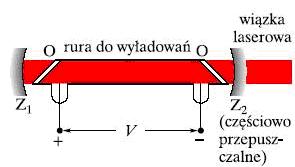
Przyłożone napięcie V powoduje przepływ elektronów przez rurę do wyładowań wypełniną mieszanina gazwoego helu i neonu. Elektrony zderzeja się z atomami helu, które emituja swiatło w całej dł.rury. Światło to przechodzi przez przepuszczalne okienka O i odbijaja się od zwierciadeł Z₁ i Z₂, przechodzac tam i z powrotem, i powodując silniejszą emisję wiatła przez atomy neonu. Część światła wydostaje się przez zwierciado Z₂, tworząc wiązkę laserową o dłufości fali λ=623,8 nm.

Pomiary:

Położenie prążków dla pojedyńczej szczeliny.

L.p.	x2 [m]	x1 [m]	x'1 [m]	x'2 [m]	x1 [m]	x2 [m]	x'1 [m]	x'2 [m]
1	0,05780	0,06010	0,06960	0,07293	0,06112	0,05741	0,06894	0,07239
2	0,05735	0,06116	0,06879	0,07223	0,06112	0,05741	0,06894	0,07239
3	0,05768	0,06125	0,06925	0,07273	0,06112	0,05741	0,06894	0,07239
4	0,05720	0,06181	0,06884	0,07225	0,06112	0,05741	0,06894	0,07239
5	0,05704	0,06130	0,06824	0,07184	0,06112	0,05741	0,06894	0,07239

Obliczam położenie prązka ciemnego 1-szego i 2-go rzędu dla pojedyńczej szczeliny:

Obliczam szerokość szczeliny dla prążków 1-szego i 2-go rzędu.

Obliczam wartość średnią
.

Obliczam wartość niepewnośći maksymalnej dla
.

Dla:

Położenie prążków 1-szego rzędu dla szczeliny kołowej.

L.p.	y1 [m]	y'1 [m]	y1 [m]	y^'1 [m]
1	0,06466	0,06677	0,06438	0,06644
2	0,06445	0,06650	0,06438	0,06644
3	0,06435	0,06634	0,06438	0,06644
4	0,06428	0,06635	0,06438	0,06644
5	0,06416	0,06626	0,06438	0,06644

Obiczam położenie pierwszego minimum dla otwory kołowego:

Obliczam średnicę otworu kołowego:

Obliczam niepewność maksymalną dla
.

Wnioski:

Gdy laser emituje fale o długości
szerokość pojedynczej szczeliny

wynosi dla prążków 1-szego rzędu
, a dla prążków 2-go rzedu

Wartość średnicy otworu kołowego równa się
Wyniki mnie niezadawalaja ponieważ odczytanie wartości mierzonych i ustawienie szczeliny ekranu w środku minimów interferencyjnych było utrudnione przez budowe i ustawienie aparatury pomiarowej.

---