Metoda TOP-DOWN: problem jest zdefiniowany na podproblemy, podproblemy są rozwiązywane a rezultaty rozwiązań podproblemów są rozwiązaniem całego problemu (np. dziel i zwyciężaj).

Rekurencja: polega na wywoływaniu algorytmu przez siebie, musi istnieć warunek kończący wykonywanie algorytmu.

Dziel i zwyciężaj: rekurencyjny podział dużego zadania na podzadania o mniejszym rozmiarze, rozwiązanie podzadań, scalenie rozwiązań podzadań w rozwiązanie dużego zadania (np. wieże Hanoi, przeszukiwanie binarne).

Algorytmy zachłanne: za pomocą lokalnie optymalnych (zachłannych) wyborów można uzyskać optymalne rozwiązanie całego zadania.

Programowanie dynamiczne - jest to metoda rozwiązywania problemów (najczęściej optymalizacyjnych czyli najoptymalniejszych), w której to problem dzieli się na mniejsze podproblemy, a następnie korzystając z rozwiązanych podproblemów rozwiązujemy problem główny (poszczególne rozwiązania są zapamiętywane w pamięci i później tylko wykorzystywane).

Algorytm zachłanny - algorytm, który w celu wyznaczenia rozwiązania w każdym kroku dokonuje zachłannego tj najlepiej rokującego w danym momencie wyboru rozwiązania częściowego. Nie patrzy on czy w następnych krokach jest sens wykonać dane działanie, tylko dokonuje decyzji lokalnie optymalnej (wydającej się w tej chwili najlepszej). Następnie kontynuuje działanie korzystając z podjętych wcześniej decyzji.

Metoda dziel i zwyciężaj - polega na rekurencyjnym dzieleniu problemu na dwa lub więcej mniejszych podproblemów tego samego (lub podobnego) typu tak długo, aż fragmenty staną się wystarczająco proste do bezpośredniego rozwiązania. Następnie otrzymane rozwiązania podproblemów scala się uzyskując rozwiązanie całego problemu.

Problem komiwojażera (zachłanny):

Wejście: lista miast i odległości, miasto startowe.

Wyjście: kolejność odwiedzania miast.

1. Jako wierzchołek aktualny przyjmujemy miasto startowe.

2. Dopóki są nie odwiedzone miasta.

3. Wybierz najkrótszą trasę z możliwych.

4. Zaznacz aktualny jako odwiedzony.

5. Dodaj aktualny do listy odwiedzonych.

6. Za aktualny podstaw końcowy z najkrótszą trasą.

Problem plecakowy:

Wejście: lista przedmiotów z wagami i wartościami, udźwig plecaka.

Wyjście: lista zabranych przedmiotów.

1. Przeliczamy wartość na kilogram dla każdego przedmiotu.

2. Sortujemy przedmioty według wartości na kilogram (malejąco).

3. Dopóki ciężar przedmiotów w plecaku jest mniejszy lub równy udźwigowi.

4. Wkładamy do plecaka kolejny możliwy najcenniejszy przedmiot

- usuwamy go z listy przedmiotów.

- dodajemy go do listy przedmiotów zabranych.

Problem plecakowy ciągły:

Wejście: lista przedmiotów z wagami i wartościami, udźwig plecaka.

Wyjście: lista zabranych przedmiotów.

1. Przeliczamy wartość na kilogram dla każdego przedmiotu.

2. Sortujemy przedmioty według wartości na kilogram (malejąco).

3. Dopóki ciężar przedmiotów (substancji) w plecaku jest mniejszy lub równy udźwigowi.

4. Wkładamy do plecaka kolejny możliwy najcenniejszy przedmiot lub jego substancję (jeśli waga przedmiotu nie pozwala na włożenie go w całości).

- usuwamy go z listy przedmiotów.

- dodajemy go do listy przedmiotów zabranych (wraz z informacją dotyczącą wagi substancji).

Problem wydawania reszty:

Wejście: wartość reszty, lista banknotów z wartościami.

Wyjście: lista banknotów użytych do wydania reszty.

1. Sortujemy listę banknotów ze względu na wartości (malejąco).

2. Dopóki wartość banknotów do wydania jest mniejsza bądź równa wartości reszty.

3. Dodajemy banknot (z listy banknotów) do listy banknotów użytych do wydania reszty.

4. Usuwamy banknot z listy banknotów.

Problem dyliżansu:

Wejście: lista miast, lista tras z kosztami, miasto startowe i końcowe.

Wyjście: kolejność odwiedzania miast.

1. Jako wierzchołek aktualny przyjmujemy miasto startowe.

2. Dopóki nie odwiedziliśmy miasta końcowego.

3. Wybierz najtańszą trasę z możliwych.

4. Zaznacz aktualny jako odwiedzony.

5. Dodaj aktualny do listy odwiedzonych.

6. Za aktualny podstaw końcowy z najkrótszą trasą.

Problem sprawdzenia czy dana liczba występuje w ciągu (dziel i zwyciężaj):

Wejście: posortowany ciąg liczb.

Wyjście: odpowiedź czy liczba x występuje w ciągu.

1. Wybieramy środkowy element ciągu.

2. Dopóki nie skończyliśmy przeszukiwać ciągu (dopóki nie można ciągu podzielić na podciągi).

3. Sprawdzamy czy środkowy element jest równy liczbie x, jeśli tak to kończymy działanie algorytmu i wypisujemy „TAK”, jeśli nie:

4. Sprawdzamy czy liczba x jest mniejsza, czy większa od środkowego elementu.

5. Wywołujemy rekurencyjne algorytm, jako ciąg rozumiemy teraz podciąg zaczynający się od pierwszego elementu tablicy a kończący na środkowym elemencie (w przypadku gdy liczba x jest mniejsza od środkowego elementu) lub podciąg zaczynający się od środkowego elementu ciągu a kończący się na ostatnim elemencie ciągu (w przypadku gdy liczba x jest większa od środkowego elementu).

Problem wyszukiwania MAX (dziel i zwyciężaj):

Wejście: nie posortowany ciąg liczb.

Wyjście: największa liczba z ciągu.

1. Jeśli ciąg jest dwuelementowy wybieramy element większy i kończymy działanie algorytmu.

2. Dzielimy ciąg na podciągi dwuelementowe.

3. Porównujemy ze sobą elementy w podciągach (wybieramy największy element z podciągu) i wywołujemy algorytm rekurencyjnie z większymi elementami z podciągów jako nowy ciąg.

Problem wyszukania n-tego elementu ciągu Fibonacciego:

Wejście: indeks (n) szukanego elementu.

Wyjście: szukany element.

1. Dla n=1 i n=2 F(n)=1.

2. Jeśli n<=2 zwracamy element o wartości 1.

3. Wywołujemy rekurencyjnie algorytm dla F(n-2)+F(n-1)

Algorytm Dijkstry - znajduje w grafie wszystkie najkrótsze ścieżki pomiędzy wybranym wierzchołkiem a wszystkimi pozostałymi. Dodatkowo wylicza również koszt przejścia każdej z tych ścieżek. Bardzo ważnym założeniem w algorytmie Dijkstry są nieujemne wagi krawędzi. Jeśli krawędzie mogą przyjmować wagi ujemne, to NIE WOLNO stosować algorytmu Dijkstry.

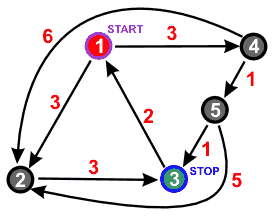
Od wierzchołka 1 do wierzchołka 3 można dojść wieloma różnymi ścieżkami: ścieżka nr 1:  1 - 2 - 3; ścieżka nr 2:  1 - 4 - 5 - 3; ścieżka nr 3:  1 - 4 - 5 - 2 - 3; ścieżka nr 4:  1 - 4 - 2 - 3

ścieżka nr 1 - koszt = 3 + 3 = 6; ścieżka nr 2 - koszt = 3 + 1 + 1 = 5; ścieżka nr 3 - koszt = 3 + 1 + 5 + 3  = 12; ścieżka nr 4 - koszt = 3 + 6 + 3 = 12

Sortowanie bąbelkowe (polega na porównywaniu dwóch kolejnych elementów i zamianie ich kolejności, jeżeli zaburza ona porządek, w jakim się sortuje tablicę. Sortowanie kończy się, gdy podczas kolejnego przejścia nie dokonano żadnej zmiany):

Wejście: nieposortowany ciąg liczb (d) o n elementach.

Wyjście: posortowany ciąg liczb (d).

1. Dla j=1,2,…,n-1

2. Dla i=1,2,…,n-1

3. Jeśli d[i]>d[i+1]

4. d[i]d[i+1];

Sortowanie przez wybieranie (polega na wyszukaniu elementu mającego się znaleźć na zadanej pozycji i zamianie miejscami z tym, który jest tam obecnie. Operacja jest wykonywana dla wszystkich indeksów sortowanej tablicy):

Wejście: nieposortowany ciąg liczb (d) o n elementach.

Wyjście: posortowany ciąg liczb (d).

1. Dla j=1,2,…,n-1

2. min=j; //min - zmienna przechowująca indeks minimalnej wartośći

3. Dla i=j+1,j+2,…,n

4. Jeśli d[i]<d[min]

5. min=i;

6. d[j]d[min];

1. Wyszukanie minimalnej (rosnąco) lub maksymalnej (malejąco) wartości z ciągu spośród elementów od i+1 do końca tablicy.

2. Zamień wartość minimalną/maksymalną z elementem na pozycji i

Sortowanie przez wstawianie (polega na usuwaniu pewnego elementu z danych wejściowych i wstawianiu go na odpowiednie miejsce w wynikach, wybór następnego elementu z danych jest dowolny):

Wejście: nieposortowany ciąg liczb (d) o n elementach.

Wyjście: posortowany ciąg liczb (d).

1. Dla j=n-1,n-2,…,1

2. x=d[j]; i=j+1;

3. Dopóki (i<=n) i (x>d[i])

4. d[i-1]=d[i]; i=i+1;

5. d[i-1]=x;

1. Utwórz zbiór elementów posortowanych i przenieś do niego dowolny element ze zbioru nieposortowanego.

2. Dopóki zbiór elementów nieposortowanych jest niepusty.

3. Weź dowolny element ze zbioru nieposortowanego.

4. Wyciągnięty element porównuj z kolejnymi elementami zbioru posortowanego póki nie napotkasz elementu równego lub elementu większego (jeśli chcemy otrzymać ciąg niemalejący) lub nie znajdziemy się na początku/końcu zbioru posortowanego.

5. Wyciągnięty element wstaw w miejsce gdzie skończyłeś porównywać.

Sortowanie przez scalanie (rekurencyjny algorytm sortowania danych, mający zastosowanie przy danych dostępnych sekwencyjnie (po kolei, jeden element na raz), na przykład w postaci listy jednokierunkowej (tj. łączonej jednostronnie) albo pliku sekwencyjnego):

Wyróżnić można trzy podstawowe kroki:

1. Podziel zestaw danych na dwie, równe części (w przypadku nieparzystej liczby wyrazów jedna część będzie o 1 wyraz dłuższa);

2. Zastosuj sortowanie przez scalanie dla każdej z nich oddzielnie, chyba że pozostał już tylko jeden element;

3. Połącz posortowane podciągi w jeden.

Procedura scalania dwóch ciągów A[1..n] i B[1..m] do ciągu C[1..m+n]:

1. Utwórz wskaźniki na początki ciągów A i B → i=1, j=1

2. Jeżeli ciąg A wyczerpany (i>n), dołącz pozostałe elementy ciągu B do C i zakończ pracę.

3. Jeżeli ciąg B wyczerpany (j>m), dołącz pozostałe elementy ciągu A do C i zakończ pracę.

4. Jeżeli A[i] ≤ B[j] dołącz A[i] do C i zwiększ i o jeden, w przeciwnym przypadku dołącz B[j] do C i zwiększ j o jeden

5. Powtarzaj od kroku 2 aż wszystkie wyrazy A i B trafią do C

Sortowanie szybkie (działa rekurencyjnie - wybierany jest pewien element tablicy, tzw. element osiowy, po czym na początek tablicy przenoszone są wszystkie elementy mniejsze od niego, na koniec wszystkie większe, a w powstałe między tymi obszarami puste miejsce trafia wybrany element, następnie sortuje się osobno początkową i końcową część tablicy, rekurencja kończy się, gdy kolejny fragment uzyskany z podziału zawiera pojedynczy element, jako że jednoelementowa podtablica nie wymaga sortowania.):

1. i=(lewy+prawy)/2;

2. piwot=d[i]; d[i]=d[prawy]; j=lewy;

3. Dla i=lewy,lewy+1,…,prawy-1

4. Jeśli d[i]>=piwot

5. Dokonaj kolejnego obiegu pętli (Krok 3).

6. d[i]d[j]; j=j+1;

7. d[prawy]=d[j]; d[j]=piwot;

8. Jeśli lewy<j-1

9. Wywołujemy rekurencyjnie algorytm sortowania szybkiego z parametrami (lewy,j-1).

10. Jeśli j+1<prawy

11. Wywołujemy rekurencyjnie algorytm sortowania szybkiego z parametrami (j+1,prawy).

Sortowanie przez kopcowanie:

1. Budowanie kopca.

2. Usunięcie elementu z korzenia i wstawienie na początek (rosnąco) lub na koniec (malejąco) posortowanej listy.

3. Wstawienie ostatniego elementu do korzenia.

4. Przywrócenie własności kopca.

Sortowania stabilne: bąbelkowe, przez wstawianie, przez scalanie, przez zliczanie, kubełkowe, pozycyjne, biblioteczne.

Sortowania niestabilne: przez wybieranie, Stella, grzebieniowe, szybkie, introspektywne, przez kopcowanie.

Reprezentacja grafów

Macierz incydencji grafu zorientowanego (skierowanego) G = (V, K) o zbiorze wierzchołków V = v₁,...,v_n i krawędzi K = k₁,..,k_m nazywamy macierz M = (m_ij), gdzie i=1,...,n oraz j=1,...,m taką, że:

Macierz sąsiedztwa (w teorii grafów) (multi)grafu G jest kwadratową macierzą w której a_ij oznacza liczbę krawędzi pomiędzy wierzchołkami i i j. W przypadku grafów prostych macierz sąsiedztwa jest macierzą zerojedynkową z zerami na głównej przekątnej. Dla grafów nieskierowanych macierz sąsiedztwa jest z definicji symetryczna.

Lista sąsiedztwa Drugą popularną reprezentacją grafu są tzw. listy sąsiedztwa - dla każdego wierzchołka zapamiętywana jest lista sąsiadujących z nim wierzchołków, np.:

Przeszukiwanie wszerz (ang. Breadth-first search, w skrócie BFS) - w informatyce algorytm przeszukiwania grafu używany do przechodzenia lub przeszukiwania drzewa lub grafu. Algorytm zaczyna od korzenia i odwiedza wszystkie połączone z nim węzły. Następnie odwiedza węzły połączone z tymi węzłami i tak dalej, aż do odnalezienia celu.

Przeszukiwanie w głąb (ang. Depth-first search, w skrócie DFS) - w informatyce algorytm przeszukiwania grafu używany do przechodzenia lub przeszukiwania drzewa lub grafu. Przeszukiwanie zaczyna się od korzenia i porusza się w dół do samego końca gałęzi, po czym wraca się o jeden poziom i próbuje kolejne gałęzie itd.

Drzewem rozpinającym (ang. Spanning Tree) grafu G nazywamy drzewo, które zawiera wszystkie wierzchołki grafu G, zaś zbiór krawędzi drzewa jest podzbiorem zbioru krawędzi grafu.

Konstrukcja drzewa rozpinającego polega na usuwaniu z grafu tych krawędzi które należą do cykli. Najmniejszą liczbą krawędzi jaką trzeba usunąć z grafu, aby graf stał się acykliczny (stał się drzewem) nazywa się rzędem acykliczności grafu lub liczbą cyklometryczną.

Minimalne drzewo rozpinające (ang. MST, Minimum Spanning Tree ) jest to drzewo rozpinające danego grafu o najmniejszej z możliwych wag, tj. takie, że nie istnieje dla tego grafu inne drzewo rozpinające o mniejszej sumie wag krawędzi.

Algorytm Prima lub algorytm Dijkstry-Prima - algorytm zachłanny wyznaczający tzw. minimalne drzewo rozpinające (MDR). Mając do dyspozycji graf nieskierowany i spójny, tzn. taki w którym krawędzie grafu nie mają ustalonego kierunku oraz dla każdych dwóch wierzchołków grafu istnieje droga pomiędzy nimi, algorytm oblicza podzbiór E' zbioru krawędzi E, dla którego graf nadal pozostaje spójny, ale suma kosztów wszystkich krawędzi zbioru E' jest najmniejsza możliwa.

Algorytm Prima wygląda tak:

• utwórz drzewo zawierające jeden wierzchołek, dowolnie wybrany z grafu,

• powtarzaj, dopóki drzewo nie obejmuje wszystkich wierzchołków grafu:

• wśród krawędzi, których jeden wierzchołek należy do drzewa, a drugi nie, wybierz krawędź o najmniejszej wadze; jeśli takich gałęzi jest wiele, wybierz dowolną z nich,

• dodaj tę krawędź wraz z drugim wierzchołkiem do drzewa.

Algorytm Kruskala wyznacza minimalne drzewo rozpinające dla grafu nieskierowanego ważonego, o ile jest on spójny. Innymi słowy, znajduje drzewo zawierające wszystkie wierzchołki grafu, którego waga jest najmniejsza możliwa. Jest to przykład algorytmu zachłannego.

Algorytm

• Utwórz las L z wierzchołków oryginalnego grafu - każdy wierzchołek jest na początku osobnym drzewem.

• Utwórz zbiór S zawierający wszystkie krawędzie oryginalnego grafu.

• Dopóki S nie jest pusty:

• Wybierz i usuń z S krawędź o minimalnej wadze.

• Jeśli krawędź ta łączyła dwa różne drzewa, to dodaj ją do lasu L, tak aby połączyła dwa odpowiadające drzewa w jedno.

• W przeciwnym wypadku odrzuć ją.

Po zakończeniu algorytmu L jest minimalnym drzewem rozpinającym.

Sortowanie topologiczne (w teorii grafów) skierowanego grafu acyklicznego to liniowe uporządkowanie wierzchołków, w którym jeśli istnieje krawędź skierowana prowadząca od wierzchołka x do y, to x znajdzie się przed wierzchołkiem y. Innymi słowy, każdy wierzchołek poprzedza wszystkie te wierzchołki, do których prowadzą wychodzące od niego krawędzie.

Wierzchołki w każdym grafie acyklicznym skierowanym można posortować topologicznie na jeden lub więcej sposobów.

Usuwanie wierzchołków "niezależnych"

Jeden z takich algorytmów polega na stopniowym usuwaniu z grafu wierzchołków o stopniu wchodzącym 0 wraz z wychodzącymi z nich krawędziami. Kolejność, w jakiej wierzchołki będą usuwane, jest poszukiwanym rozwiązaniem.

Jeśli po usunięciu wszystkich takich wierzchołków (wraz z krawędziami) graf nie pozostanie pusty, oznacza to, że zawiera cykle.

By zastosować powyższy algorytm, należy wykorzystać kontener, w którym przechowywane będą wierzchołki do usunięcia.

Q ← Kolejka z wierzchołkami o stopniu wchodzącym równym 0

dopóki Q jest niepusta rób

usuń wierzchołek n z przodu kolejki Q

wypisz n

dla każdego wierzchołka m o krawędzi e od n do m rób

usuń krawędź e z grafu

jeżeli do m nie prowadzi żadna krawędź to

wstaw m do Q

jeżeli graf ma wierzchołki to

wypisz komunikat o błędzie (graf zawiera cykl)

Wykorzystanie algorytmu DFS

Kolejny algorytm, którym można się posłużyć jest DFS. Wystarczy, że podczas wykonywania jego tradycyjnej wersji będziemy na początek listy dodawać aktualnie przetworzony wierzchołek, a otrzymamy listę w pożądanym porządku.

L ← Lista wierzchołków posortowanych w kolejności topologicznej

dla każdego wierzchołka rób

jeśli nie był jeszcze odwiedzony

dla każdej krawędzi z niego wychodzącej rób

jeśli prowadzi do nieodwiedzonego jeszcze wierzchołka

ustaw go jako odwiedzonego i przetwórz rekurencyjnie

wstaw wierzchołek na początek listy

Wyszukiwanie wzorca

Algorytm „naiwny” wyszukiwania wzorca:

P - wzorzec, T - tekst

1. n=długość[T]; m=długość[P];

2. Dla s=0 do n-m

3. Jeśli P[1..m]==T[s+1..s+m]

4. Wypisz „Wzorzec występuje z przesunięciem” s

Algorytm Rabina-Karpa:

P, T, d -liczba zwykle równa |Σ|, q - liczba pierwsza

1. n=długość[T]; m=Długość[P]; h=d^m-1mod q; p=0; t₀=0;

2. Dla i=1 do m

3. p=(dp+P[i])mod q;

4. t₀=(dt₀+T[i])mod q;

5. Dla s=0 do n-m

6. Jeśli p==t_s

7. Jeśli P[1..m]=T[s+1..s+m]

8. Wypisz „Wzorzec występuje z przesunięciem” s

9. Jeśli s<n-m

10. t_s+1=(d(t_s-T[s+1]h)+T[s+m+1])mod q

Wyszukiwanie wzorca z wykorzystaniem automatów skończonych:

δ - funkcja przejść

1. n=długość[T], q=0;

2. Dla i=1 do n

3. q=δ(q,T[i])

4. Jeśli q==m

5. s=i-m

6. Wypisz „Wzorzec występuje z przesunięciem” s

Obliczanie funkcji przejść (P,Σ):

1. m=długość[P];

2. Dla q=0 do m

3. Dla a
Σ

4. k=min(m+1,q+2);

5. Rób k=k-1 dopóki P_k
P_qa

6. δ(q,a)=k

7. Zwróć δ

Algorytm Knutha-Morrisa-Pratta:

1. n=długość[T]; m=długość[P]; π=funkcja prefiksowa(P); q=0;

2. Dla i=1 do n

3. Dopóki q>0 i P[q+1]!=T[i]

4. q=π[q];

5. Jeśli P[q+1]=T[i]

6. q=q+1;

7. Jeśli q==m

8. Wypisz „Wzorzec występuje z przesunięciem” i-m

9. q=π[q];

Funkcja prefiksowa(P):

1. m=długość[P]; π[1]=0; k=0;

2. Dla q=2 do m

3. Dopóki k>0 i P[k+1]P!=[q]

4. k=π[k];

5. Jeśli P[k+1]==P[q]

6. k=k+1;

7. π[q]=k;

8. Zwróć π.

Algorytm Boyera-Moore'a:

1. n=długość[T]; m=długość[P]; λ=Heurystyka niezgodnośći(P,m,Σ); γ=Heurystyka dobrego sufiksu(P,m); s=0;

2. Dopóki s<=n-m

3. j=m;

4. Dopóki j>0 i P[j]==T[s+j]

5. j=j-1;

6. Jeśli j==0

7. Wypisz „Wzorzec występuje z przesunięciem” s

8. s=s+γ[0];

9. W przeciwnym wypadku

10. s=s+max(γ[j],j-λ[T[s+j]])

Heurystyka niezgodności(P,m,Σ):

1. Dla każdego symbolu a
Σ

2. λ[a]=0;

3. Dla j=1 do m

4. λ[P[j]]=j;

5. Zwróć λ.

Heurystyka dobrego sufiksu(P,m):

1. π=Funkcja prefiksowa(P); P'=odwrócone P; π'=Funkcja prefiksowa(P');

2. Dla j=0 do m

3. γ[j]=m-π[m];

4. Dla l=1 do m

5. j=m-π'[l];

6. Jeśli γ[j]>l-π'[l]

7. γ=l-π'[l];

8. Zwróć γ.

---