Algorytm
znaczenie cybernetyczne
Jest to dokładny przepis wykonania w określonym porządku skończonej liczby operacji, pozwalający na rozwiązanie zbliżonych do siebie klas problemów.
znaczenie matematyczne
Jest to reguła przekształcania wyrażeń matematycznych przez powtarzanie tych samych działań na kolejno otrzymanych wynikach działań poprzednich.
Słowo „algorytm” pochodzi od perskiego matematyka Mohammed ibn Musa al-Kowarizimi ( Algorismus -
łacina) z IX w. ne.
Krótka historia algorytmów
365-300 p.n.e - Euklides : pierwsze znane algorytmy
17, 18 wiek - Blaise Pascal, Wilhelm von Leibnitz -
pierwsze „nowoczesne algorytmy” liczenia w różnych systemach
1801 - Jacquard, krosno tkackie z algorytmem na kartach perforowanych
1833 - Charles Babbage - maszyna różnicowa, algorytm różnicowy
1892- Hermann Hollerith - maszyna i algorytm do opracowywania danych statystycznych
1930 - Alan Turing, Kurt Godel - prace z teorii algorytmów , maszyna Turinga
1940 - 50 - John von Neumann - współczesna koncepcja budowy komputera i uruchamiania programów
Poziomy abstrakcji w prezentacji algorytmów:
- język naturalny (maksymalny poziom abstrakcji -
niejednoznaczność sformułowań)
- konwencja notacyjna z pogranicza języka naturalnego i języka programowania (pseudo-kod)
- SCHEMAT BLOKOWY
- język programowania (FORTRAN, PASCAL, C++ )
- język maszynowy ( minimalny poziom abstrakcji -
brak ogólności rozważań, opis trudny do analizy)
Schemat blokowy to:
1. Schemat układu (diagram) czyli graficzny sposób zobrazowania przedstawiający bloki realizujące określone funkcje oraz wzajemne powiązania między blokami
2. Sieć działań czyli graficzny sposób zapisu algorytmu w postaci połączonych liniami i strzałkami skrzynek (bloków) operacyjnych (obliczeniowych),
warunkowych i innych.



Skrzynki schematów blokowych /konwencja/:
1. Skrzynki START i STOP
2. Skrzynka deklaracji zmiennych
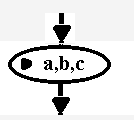
3. Skrzynka wprowadzania danych
Skrzynka wyprowadzania wyników
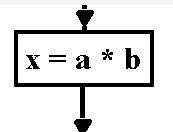
4. Skrzynka wyliczeniowa (instrukcja przypisania)
5. Skrzynka warunkowa
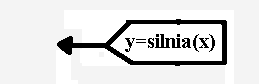
6. Skrzynka wywołania podprogramu
Schemat blokowy jest graficznym przedstawieniem zbioru operacji tworzących pełny algorytm i
wzajemnych powiązań między nimi, uwzględniający kolejność wykonywania operacji.
Zasady budowania schematów blokowych:
- każda operacja, relacja lub informacja jest umieszczana w skrzynce
- kolejność wykonywania operacji wyznaczają
połączenia między skrzynkami
- każde połączenie jest zaczepione początkiem do skrzynki, a końcem do innej skrzynki lub innego połączenia, żadne połączenie nie rozdziela się
- rozgałęzienie sieci działań możliwe jest tylko dzięki skrzynkom warunkowym
- schemat posiada jedną skrzynkę START i co
najmniej jedną skrzynkę STOP
- ze skrzynki START można przejść do skrzynki STOP
poruszając się po sieci działań
- ze skrzynki START można dotrzeć wzdłuż połączeń do dowolnej innej skrzynki schematu
- z każdej skrzynki istnieje przejście wzdłuż połączeń do jednej ze skrzynek STOP
Trzy struktury schematów blokowych
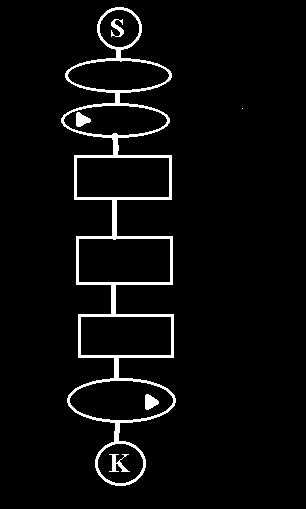
1) Schemat blokowy liniowy
Schemat blokowy liniowy występuje w zadaniach, w których każda z operacji elementarnych nie zawiera relacji (warunku) i powtórzeń (iteracji).
Realizacja poszczególnych sąsiednich operacji
następuje według ustalonej kolejności od operacji początkowej do końcowej.
Przykłady: liczenie pola powierzchni, obwodu figur płaskich i wiele innych prostych zadań.
2) Schemat blokowy z rozgałęzieniami
Schematy blokowe z rozgałęzieniami spotyka się w zadaniach dla których kolejność poszczególnych etapów w rozwiązaniu może się zmieniać w zależności od warunków określonych w sformułowaniu
problemu.

Cechą tych algorytmów jest to, iż w trakcie realizacji przechodzi się tylko po jednej z możliwych dróg, przy czym każdy oddzielny etap realizacji algorytmu wykonywany jest dokładnie jeden raz.
W rozwiązaniach można wykorzystywać drzewa
logiczne.
Przykłady: znajdowanie liczby najmniejszej, rozwiązanie równania liniowego i kwadratowego
3) Schemat blokowy cykliczny - z pętlą
a) ze sprawdzeniem warunku b) ze sprawdzeniem na początku warunku na końcu
Algorytmy dla problemów wymagających powtarzania poszczególnych etapów procesu obliczeniowego
nazywamy cyklicznymi (czyli z pętlą).
Przez pętlę w schemacie blokowym rozumiemy tą część schematu, która opisuje drogę (obwód) zamkniętą zgodnie z kierunkiem połączenia (obiegu).
Pętla stanowi graficzny opis powtarzania czynności.
Ciąg wszystkich czynności wykonywanych przy
jednokrotnym przebiegu pętli nazywamy cyklem pętli.
W każdej pętli musi wystąpić:
• co najmniej jedna skrzynka operacyjna
(np. wyliczeniowa) zawierająca opis powtarzanej czynności,
• modyfikacja w każdym cyklu co najmniej jednej wartości zmiennej występującej w pętli,
• skrzynka decyzyjna z warunkiem, czy pętla ma być nadal powtarzana czy też zakończona.
Często w pętli występują zmienne nazywane licznikami, których wartości w algorytmie określają ilość
zrealizowanych cykli pętli.
Metody nadania wartości zmiennej poprzez:
• wprowadzenie danej
• przypisanie wartości
• przypisanie nowej wartości (modyfikacji wartości zmiennej)
Cechy każdego poprawnego algorytmu:
• Posiada dane wejściowe – niekoniecznie w formie numerycznej – pochodzące z dobrze zdefiniowanego źródła
• Produkuje pewien wynik – niekoniecznie numeryczny
• Jest precyzyjnie zdefiniowany, tzn. każdy krok algorytmu musi być jednoznacznie określony
• Jest skończony – wynik algorytmu musi być „kiedyś”
dostarczony
Na proces rozwiązywaniu zadania składa się :
• Formułowanie zadania
• Rozwiązanie zadania i zapis jego rozwiązania
• Sprawdzenie i wartościowanie rozwiązania zadania
Formułowanie zadania obejmuje:
• Wyodrębnienie danych wejściowych (założeń) i dokonanie ich weryfikacji co do poprawności
(wartościowanie)
• Stwierdzenie czy możliwe jest jego rozwiązanie
Rozwiązywanie zadania to sposób postępowania
uwzględniający:
• Dane lub założenia ze sformułowania zadania
• Realizację takich czynności jak określanie, konstruowanie, wnioskowanie, sprawdzanie i
powtarzanie
• Uzyskiwanie wyniku w postaci odpowiedzi na
postawione w zadaniu pytanie i jego wartościowanie (sprawdzenie poprawności)
Etapy w informatycznym rozwiązywaniu zadania:
• Sformułowanie zadania
• Konstruowanie algorytmu rozwiązania jako schematu postępowania
• Konstruowanie schematu blokowego - z zaznaczeniem sieci działań – jako graficznej reprezentacji
algorytmu
• Napisanie programu komputerowego jako zapisu algorytmu w ustalonym języku programowani
• Weryfikacja (tzn. analiza i testowanie) programu i jego uruchomienie
Przykłady:
1. Rozwiązać równanie 3*x+1=0 (jednostkowe zadanie) 2. Rozwiązać równanie a*x+b=0, gdy dane są liczby rzeczywiste a,b (klasa zadań)
3. Obliczyć x=(3.64*0.381) / 12.5 (jednostkowe zadanie) 4. Wyznaczyć x=(a*b)/c , gdy dane są liczby rzeczywiste a,b,c , przy czym c ≠ 0 (klasa zadań)
Document Outline
Wyszukiwarka
Podobne podstrony:
AiSD Wyklad4 dzienne id 53497 Nieznany (2)
AiSD Wyklad9 dzienne id 53501 Nieznany
AiSD Wyklad2 dzienne
AiSD Wyklad11 dzienne id 53494 Nieznany
AiSD Wyklad1 dzienne
AiSD Wyklad6 dzienne id 53499 Nieznany (2)
AiSD Wyklad7 dzienne id 53500 Nieznany (2)
AiSD Wyklad3 dzienne id 53496 Nieznany (2)
AiSD Wyklad2 dzienne
AiSD Wyklad8 dzienne
AiSD Wyklad5 dzienne id 53498 Nieznany
AiSD Wyklad4 dzienne id 53497 Nieznany (2)
AiSD wyklad 3
Współczesne systemy polityczne (wykład 2), Dziennikarstwo i komunikacja społeczna (KUL) I stopień, R
AiSD wyklad 1 id 53489 Nieznany
wyklad I dzienne cz A
Ekonomika i organizacja przedsiebiorstw wyklady dzienne i zaoczne
więcej podobnych podstron