Algorytmy z powrotami

Algorytmy z powrotami są wykorzystywane do rozwiązywania
problemów, w których z określonego zbioru jest wybierana sekwencja
obiektów tak, aby spełniała ona określone kryteria.

Klasycznym przykładem jest rozwiązanie problemu n-królowych.
Zadaniem jest ustawienie n-królowych na szachownicy n

×

n w taki

sposób, aby się wzajemnie nie szachowały.
Sekwencją w tym problemie jest n pozycji, na których są umieszczone
królowe, zbiorem dla każdego wyboru jest n

2

możliwych pól na

szachownicy. Kryterium jest takie, że królowe nie mogą się
wzajemnie szachować.

Algorytmy z powrotami są zmodyfikowanym przeszukiwaniem
drzewa ( z korzeniem ) w głąb. Na początku odwiedzamy korzeń, a
poźniej po przejściu do węzła przeglądane są wszystkie węzły
potomne.

Generalnie przeszukiwanie nie wymaga określonego porządku
odwiedzania węzłów, ale wygodniej jest gdy przeszukiwane są węzły
od lewej do prawej.

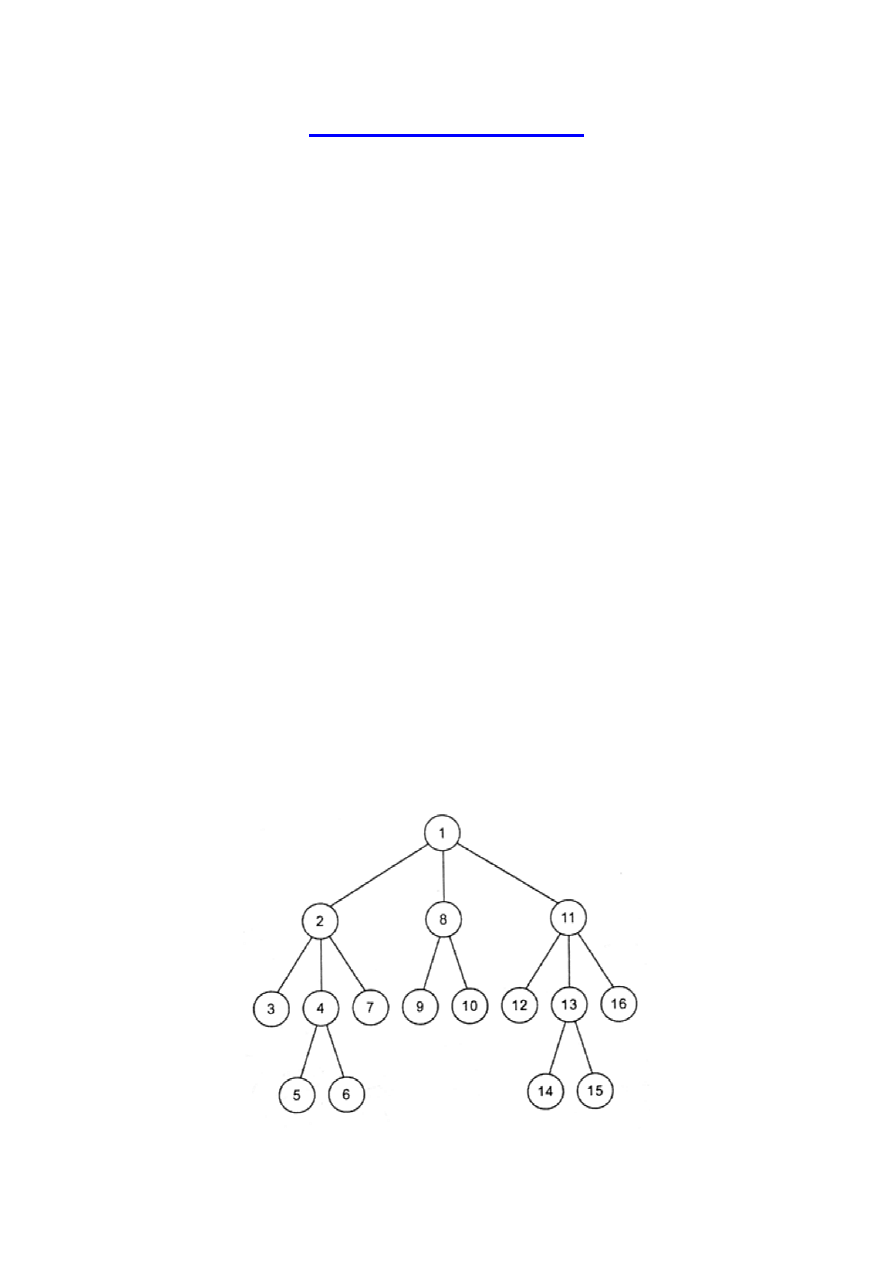
Przykład przeszukiwania drzewa w głąb z węzłami ponumerowanymi
w kolejności ich odwiedzania:

Węzły są ponumerowane w kolejności ich odwiedzania. Jak widać
podczas wyszukiwania w głąb przechodzi się po ścieżce tak głęboko,
jak jest to możliwe, aż do osiągnięcia ślepego zaułka. Następnie
wracamy do węzła z niodwiedzonymi węzłami potomnymi i znów
przechodzimy w głąb tak daleko, jak jest to możliwe.

Rozważmy ustawienie 4 królowych na szachownicy 4

× 4.

Problem można rozwiązać przez ustawienie królowych w kolejnych
wierszach i sprawdzanie, która kombinacja kolumn daje prawidłowe
rozwiązanie. Daje to 4

× 4 × 4 × 4 = 256 potencjalnych rozwiazań.

Można tworzyć potencjalne rozwiązania przez tworzenie drzewa:
w węzłach drzewa z poziomu 1 będą zapisane kolumny wybrane dla
pierwszej królowej, w węzłach poziomu 2 wybrane kolumny dla
drugiej królowej, etc.

Ścieżka od węzła głównego do liścia jest potencjalnym rozwiazaniem.
Liść to jest węzeł bez węzłów potomnych. Drzewo takie nazywamy
drzewem przestrzeni stanów.

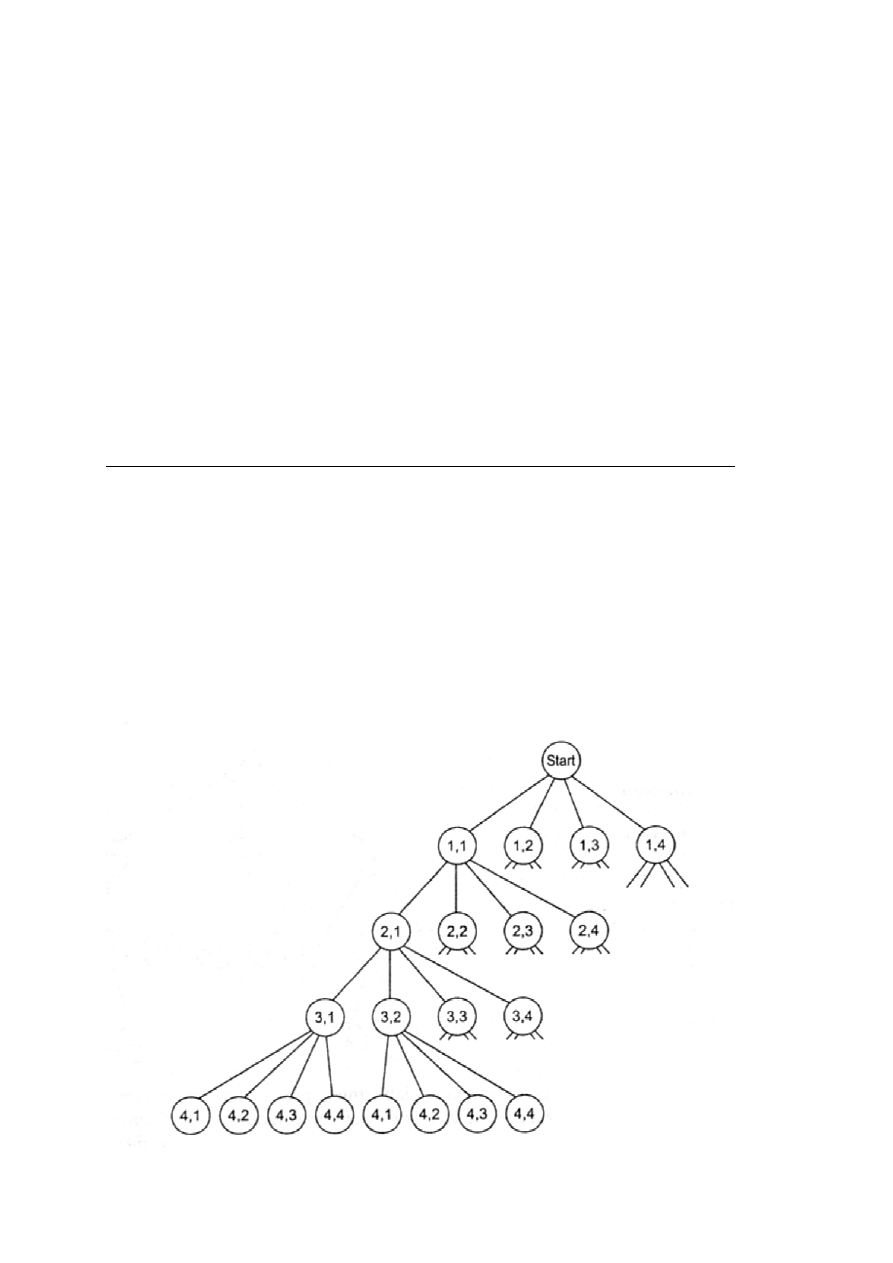
Fragment drzewa przestrzeni stanów pokazano poniżej:

Całe drzewo ma 256 liści, po jednym dla każdego potencjalnego
rozwiązania. W każdym węźle przechowywana jest para liczb <i,j>,
oznaczająca, że królowa z wiersza i jest umieszczona w kolumnie j.

Aby określić rozwiązanie, węzły są odwiedzane zgodnie z metodą
przeszukiwania w głąb, w którym węzły pochodne są odwiedzane od
strony lewej do prawej.

Pierwsze sprawdzane scieżki to:
[<1.1><2.1><3.1><4.1>]
[<1.1><2.1><3.1><4.2>]
[<1.1><2.1><3.1><4.3>]
[<1.1><2.1><3.1><4.4>]
[<1.1><2.1><3.2><4.1>]

Algorytm z powrotami jest algorytmem, w którym po zorientowaniu
się, że węzeł prowadzi do ślepego zaułka, wracamy do węzła
nadrzędnego i kontynuujemy wyszukiwanie od następnego węzła.

Węzeł nazywamy nieobiecującym, gdy w czasie jego odwiedzania
można określić, że nie może on doprowadzić do rozwiązania
(przykład poniżej).

W przeciwnym razie węzeł jest nazywany obiecującym.

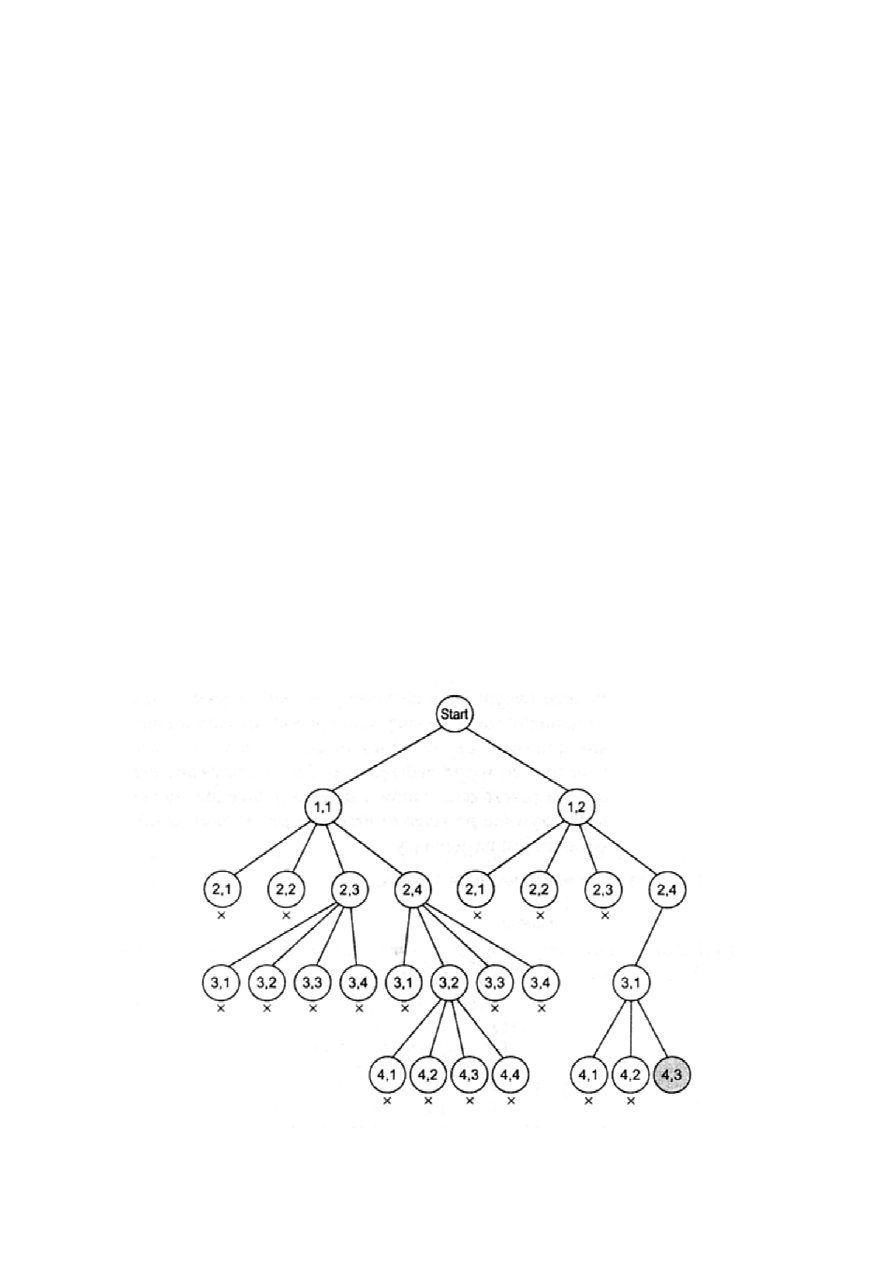
Algorytm z powrotami polega na wykonywaniu przeszukiwania w
głąb drzewa przestrzeni stanów, aby sprawdzić czy węzeł jest
obiecujący, czy nie. Jeżeli węzeł nie jest obiecujący, wracamy do
węzła nadrzędnego.

Ogólny algorytm z powrotami:

void checknode (node v)

{

node u;

if (promising(v))
if(istnieje rozwiązanie dla v)

drukuj rozwiązanie;

else

for(każdy węzeł pochodny u węzła v)

checknode(u);

}

Algorytm z powrotami jest identyczny jak przeszukiwanie w głąb,
poza tym, że węzły pochodne są odwiedzane tylko w przypadku, gdy
węzeł macierzysty jest obiecujący i nie znaleziono w nim rozwiązania

Dla problemu n-królowych funkcja promising zwraca false , jeżeli
węzeł i dowolny z jego przodków oznaczają umieszczenie królowej w
tej samej kolumnie lub przekątnej (oznaczenie x na rys.).

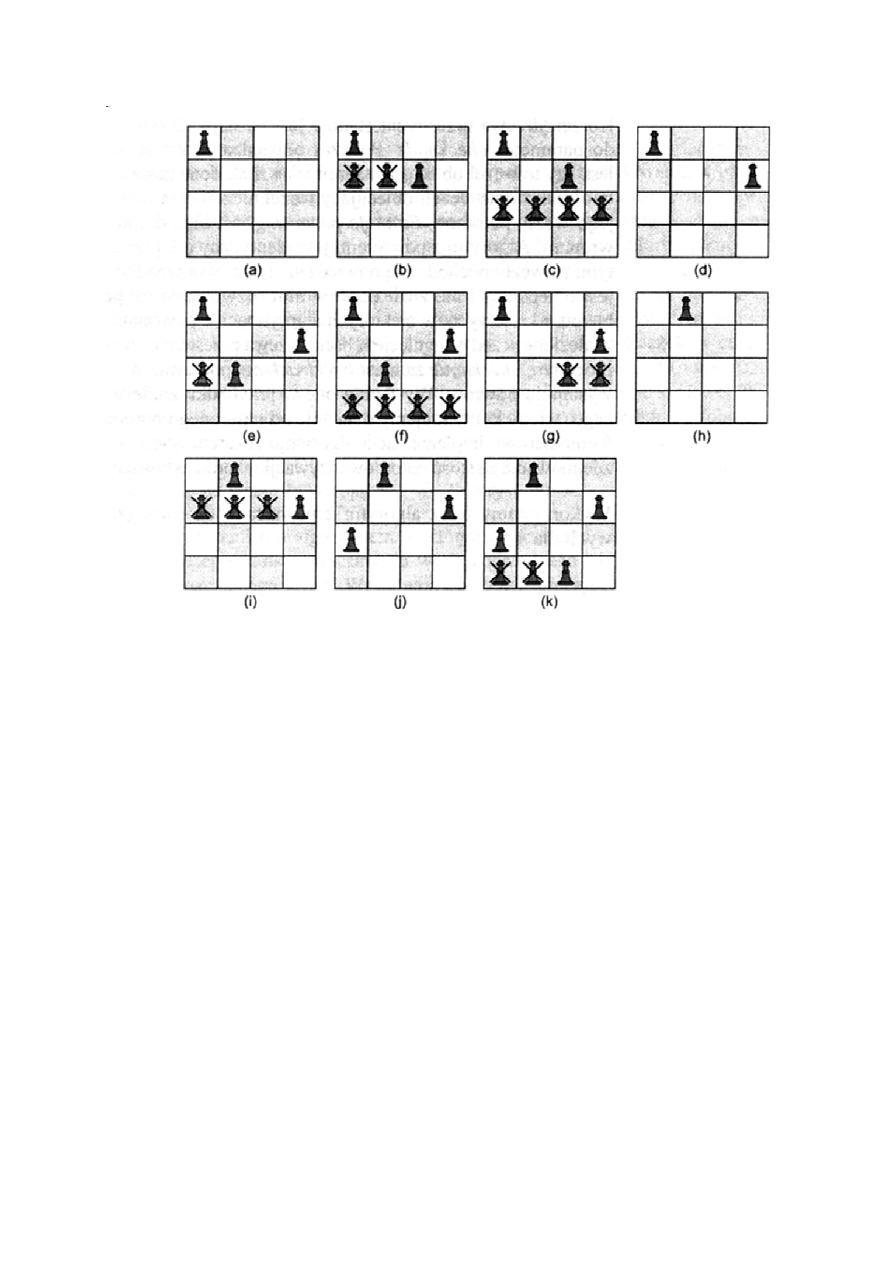
Algorytm z powrotami sprawdza 27 węzłów w celu odszukania
rozwiązania, bez zastosowania tego algorytmu trzeba sprawdzić 155
wezłów w celu odszukania tego samego rozwiązania.

Nieefektywność w ogólnym algorytmie z powrotami (procedura
checknode) wynika z faktu, że sprawdzamy czy węzeł jest obiecujący,
po przekazaniu go do procedury. Rekordy aktywacji wezłów
nieobiecujących są niepotrzebnie odkładane na stos rekordów
aktywacji.


Algorytm ze sprawdzeniem czy wezeł jest obiecujący, przed
wywołaniem rekurencyjnym, wyglądałby następujaco:

void expand (node v)
{

node u;

for (każdy węzeł pochodny u węzła v)

if (promising(u))

if (istnieje rozwiazanie dla u)

drukuj rozwiazanie;

else

expand(u);

}

Wersja poprzednia jest łatwiejsza do zrozumienia, gdyż wszystkie
operacje są wykonywane w checknode tzn. : sprawdzanie czy węzeł
jest obiecujący; jeżeli jest obiecujący to czy zawiera rozwiązanie;
drukowanie rozwiązania.

Problem n-królowych

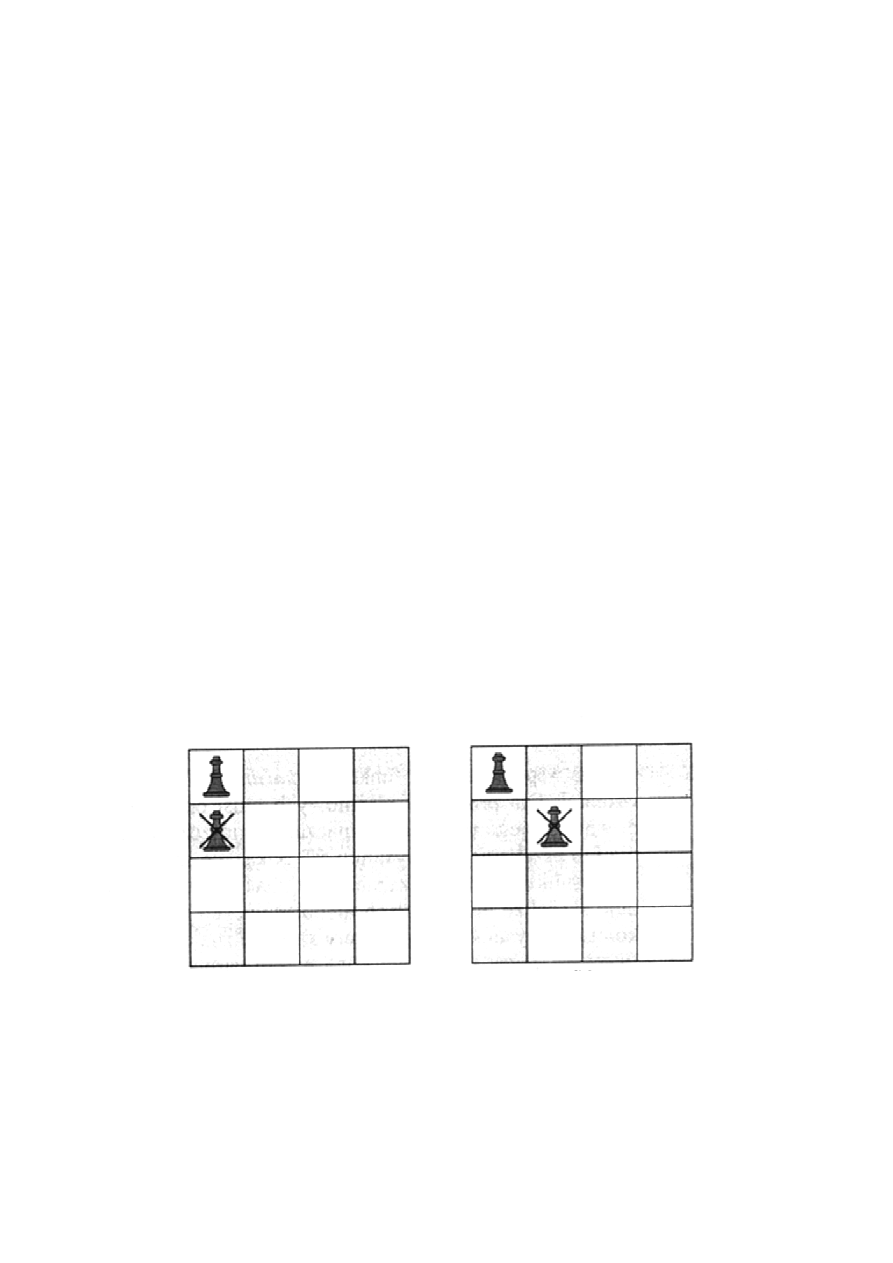
Funkcja sprawdzająca, czy węzeł jest obiecujący, musi sprawdzać, czy
dwie królowe są w tej samej kolumnie lub na tej samej przekątnej.

Sprawdzenie kolumny to:
col(i) = col(k)

gdzie col(i) jest kolumną w której jest umieszczona królowa z i-tego
wiersza.

Sprawdzenie przekątnej to:

col(i) - col(k) = i – k lub col(i) - col(k) = k – i

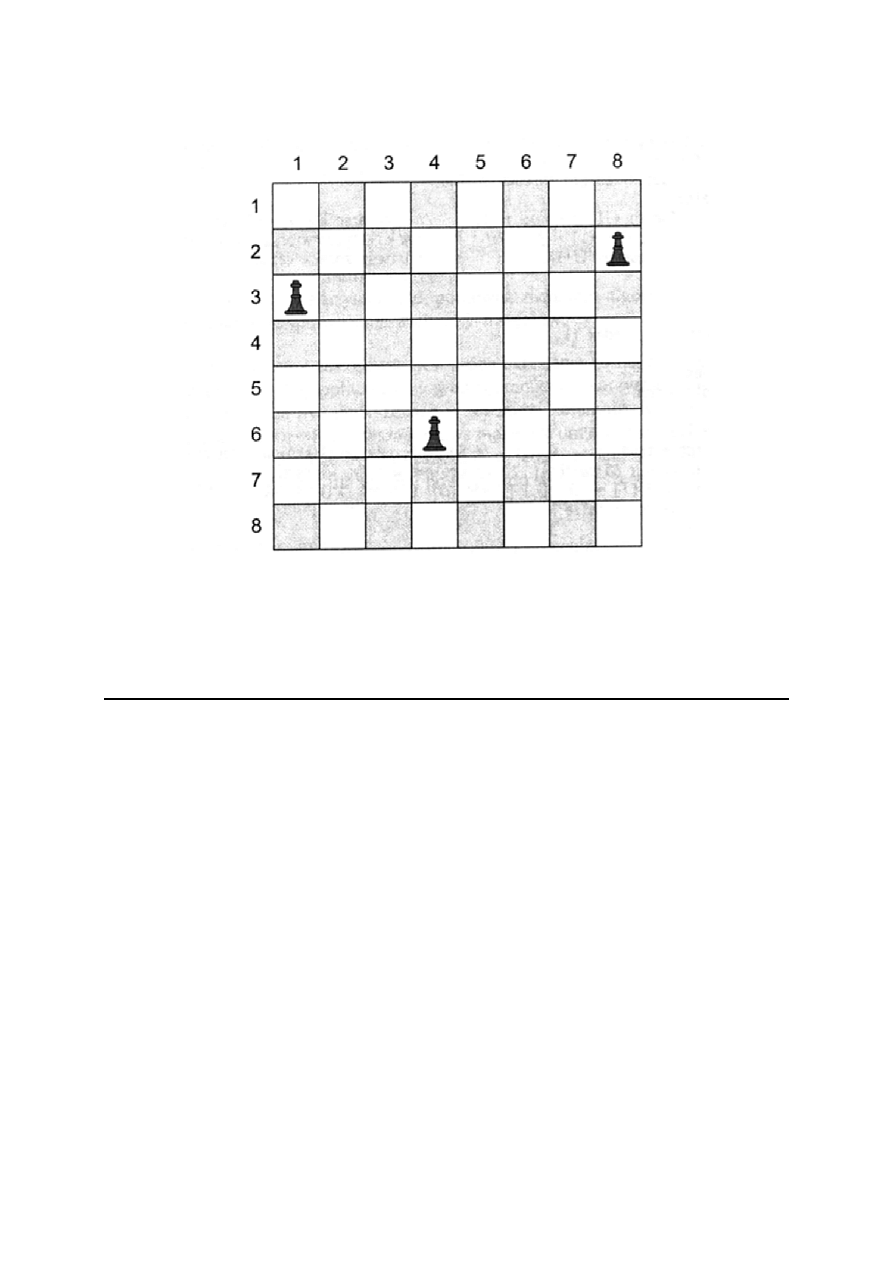
Przykładowo:

col(6) – col(3) = 4-1 = 3 = 6-3

col(6) – col(2) = 4-8 = -4 = 2-6

Algorytm z powrotami dla problemu n-królowych

Problem: umieść n królowych na szachownicy w taki sposób, żeby
żadne dwie królowe nie znalazły się w tym samym wierszu, tej samej
kolumnie oraz na tych samych przekątnych.

Dane wejściowe: dodatnia liczba całkowita n.

Wynik: wszystkie możliwe sposoby na umieszczenie n królowych na
szachownicy n

×

n tak, aby się wzajemnie nie szachowały. Każdy

wynik cząstkowy składa się z tablicy liczb całkowitych col,
indeksowanych od 1 do n, gdzie col(i) jest kolumną, w której
umieszczona została królowa z wiersza i.

void queens (index i)

{

index j;

if (promising(i) )

if(i= = n)

cout<< od col[i] do col[n];

else
for(j=1;j<=n;j++){//Sprawdzenie czy królow

col[i+1] = j; //w i+1-tym wierszu moze

queens(i+1); //byc ustawiona w kazdej

//z n kolumn

}

}

bool promising (index i)

{

index k;

bool switch;

k=1;

switch = true; //Sprawdź czy jakas

//krolowa szachuje królową

while(k<i && switch){ //w i-tym wierszu

if(col[i]==col[k] || abs(col[i]-col[k])==i-k)

switch = false;

k++;

}

return switch;

}

Algorytm powyższy tworzy wszystkie rozwiązania problemu n-
królowych. Przerobienie programu tak, aby zatrzymywał się po
znalezieniu pierwszego rozwiazania, jest proste.

W analizie algorytmu należy określić ilość sprawdzonych węzłów
jako funkcję wartości n, czyli liczby królowych. Górną granicę liczby
węzłów w drzewie przestrzeni stanów można dośc łatwo policzyć.

Drzewo zawiera 1 węzeł na poziomie 0, n węzłów na poziomie 1, n

2

węzłów na poziomie 2 oraz n

n

na poziomie n.

Całkowita liczba węzłów wynosi

1+n+n

2

+n

3

+…+n

n

= (n

n+1

– 1) / (n – 1)

Przykladowo, dla n=8 mamy

(8

8+1

– 1) / (8 – 1) = 19 173 961 węzłów

Analiza ta jest nie w pełni użyteczna bo zadaniem algorytmu z
powrotami jest uniknięcie sprawdzania wielu z tych węzłów.

Można również określić górną granicę ilości węzłów obiecujących
(dla n=8). Pierwsza królowa może być umieszczona w dowolnej z
ośmiu kolumn, druga może być umieszczona w jednej z siedmiu
kolumn. Po ustawieniu drugiej królowej dla trzeciej zostanie do
wyboru sześć kolumn. Dlatego mamy co najwyżej:

1 + 8 + 8

×7 + 8×7×6 + 8×7×6×5 + … + 8! = 109 601

obiecujących węzłów.

Ogólnie dla dowolnego n mamy co nawyżej

1 + n + n(n-1) + n(n-1)(n-2) + … + n! obiecujących węzłów.

Analiza ta nie jest pełna, gdyż po pierwsze nie bierze pod uwagę
sprawdzania przekątnych, po drugie całkowita liczba odwiedzanych
węzłów zawiera zarówno węzły obiecujące, jak i nieobiecujące.

Najprostszą metodą byloby uruchomienie programu na komputerze i
zliczanie odwiedzanych węzłów.

n Algorytm A Algorytm B Algorytm z powrotami
________________________________________________________________
Liczba węzłów Liczba potencjalnych Liczba węzłów Liczba
sprawdzanych rozwiązań n! sprawdzanych znalezionych
(bez powrotów) (rozne kolumny) (z powrotami) węzłów obiec.
________________________________________________________________
4 341 24 61 17

8 19 173 961 40 320 15 721 2057

12 9.73

×10

12

4.79

×10

8

1.01

×10

7

8.56

×10

5

14 1.20

×10

16

8.72

×10

10

3.78

×10

8

2.74

×10

7

Oczywiście, uruchamianie algorytmu w celu określenia jego
efektywności nie jest faktyczną analizą. Zadaniem analizy jest
określenie jak efektywny jest algorytm, jeszcze przed jego
uruchomieniem.

Co można zrobić w takiej sytuacji ?

Algorytmy Monte-Carlo

Drzewa przestrzeni stanów dla algorytmów z powrotami mają
wykładniczo lub szybciej roznąca liczbę węzłów. Warto zauważyć, że
jeśli mamy dwa przypadki z taką samą wartością n, jeden z nich może
wymagać sprawdzenia kilku węzłów, natomiast inne wymagają
sprawdzenia całego drzewa przestrzeni stanów.
Jeżeli oszacujemy, jak efektywny jest dany algorytm z powrotami dla
danego przypadku, możemy zdecydować, czy zastosowanie go jest
sensowne.

Algorytm Monte-Carlo to algorytm probabilistyczny. Jest to taki
algorytm, w którym następna wykonywana instrukcja jest czasami
określana w sposób losowy, zgodnie z pewnym rozkładem losowym.

Algorytm deterministyczny to taki, w którym przedstawiony
przypadek nie może mieć miejsca.
Algorytm Monte-Carlo pozwala oszacować spodziewaną wartość
zmiennej losowej, zdefiniowanej w przestrzeni próbek, na podstawie
średniej wartości losowych próbek z tej przestrzeni. Nie ma
gwarancji, że to oszacowanie jest bliskie właściwej wartości
oczekiwanej, ale prawdopodobieństwo, że jest bliskie, zwiększa się ze
wzrostem czasu działania algorytmu (ilosci uruchomień algorytmu).

Jak wykorzystać algorytm Monte-Carlo do oszacowania efektywności
algorytmu z powrotami ?

Generujemy w drzewie „typową ścieżkę”, składajacą się z węzłów,
które powinny być sprawdzone w danym przypadku, a nastepnie
szacujemy liczbę węzłów, odgałęziających się od tej ścieżki.
Oszacowanie to daje w wyniku szacunkową liczbę węzłów, które
należy sprawdzić w celu znalezienia wszystkich rozwiązań. Inaczej
mówiąc, jest to szacunkowa liczba węzłów w przeciętnym drzewie
stanów.

Muszą być spełnione dwa warunki:

• we wszystkich węzłach na tym samym poziomie drzewa

przestrzeni stanów powinna być używana ta sama funkcja
określająca, czy węzeł jest obiecujący

• węzły na tym samym poziomie w drzewie przestrzeni stanów

muszą mieć taka samą liczbę potomków.

Algorytm dla n-królowych spełnia te warunki.

Technika Monte-Carlo wymaga losowego generowania obiecującego
potomka węzła, zgodnie z rozkładem normalnym, czyli generowania
liczb losowych.

Sposób realizacji:

• niech m

0

będzie liczbą obiecujących potomków korzenia

• losowo generujemy obiecujący węzeł pochodny na poziomie 1.

Niech m

1

będzie liczbą obiecujących potomków tego węzła.

• losowo wygeneruj obiecujący węzeł dla węzła uzyskanego w

poprzednim kroku. Niech m

2

będzie liczbą obiecujących

potomków tego węzła.
……

• Losowo wygeneruj obiecujący węzeł dla węzła uzyskanego w

poprzednim kroku. Niech m

i

będzie liczbą obiecujących

potomków tego węzła.

Proces jest kontynuowany, dopóki nie zostaną znalezione żadne
obiecujące węzły potomne. m

i

jest szacunkową średnią liczbą

obiecujących węzłów na poziomie i.
Niech t

i

= całkowita liczba potomków węzła na poziomie i

Wszystkie t

i

węzłów zostaje sprawdzone i tylko m

i

obiecujacych

węzłów potomnych ma sprawdzone węzły potomne. Szacunkowa
liczba węzłów sprawdzonych przez algorytm z powrotami w celu
wyszukania wszystkich rozwiązań wynosi

1+ t

0

+ m

0

t

1

+ m

0

m

1

t

2

+ m

0

m

1

…m

i-1

t

i

+ ..

.

Ogólny algorytm obliczający tą średnią może wygladać następująco
( mprod = m

0

m

1

…m

i-1

) .

Szacowanie Monte-Carlo

Problem: oszacuj efektywność algorytmu z powrotami, korzystając z
algorytmu Monte Carlo.

Dane wejściowe: problem rozwiazywany przez algorytm z
powrotami.

Wynik: szacunkowa liczba węzłów w przyciętym drzewie przestrzeni
stanów generowanych przez algorytm, który jest liczbą węzłów, jaką
musi sprawdzić algorytm w celu znalezienia wszystkich rozwiązań
danego przypadku.

int estimate ()

{

node v;

int m,mprod,t,numnodes;

v = korzeń drzewa stanów;

numnodes = 1;

m=1;

mprod=1;
while

(m!=0) {

t=liczba potomków v;

mprod=mprod*m;

numnodes=numnodes+mprod*t;

m=liczba obiecujacych potomków v;
if

(m!=0)

v=losowo wybrany obiecujacy potomek v;

}

return numnodes;

}

Dla algorytmu problemu n-królowych może to wyglądać.

________________________________________________________
Oszacowanie metodą Monte Carlo dla algorytmu z powrotami –
problem n-królowych

Problem: oszacowanie efektywności algorytmu

Dane wejściowe: dodatnia wartość całkowita n

Wynik: szacunkowa liczba węzłów w przyciętym drzewie przestrzeni
stanów, generowanym przez algorytm – liczba węzłów, jakie muszą
zostać sprawdzone przez algorytm przed wyszukaniem wszystkich
sposobów na ustawienie n królowych na szachownicy n

×

n tak, aby

się wzajemnie nie szachowały.

int estimate_n_queens (int n)
{

index i,j,col[1..n];

int m,mprod,numnodes;

set_of_index prom_children;

i=0;

numnodes=1;

m=1;

mprod=1;

while (m!=0 && i!=n) {

mprod=mprod*m;

numnodes=numnodes+mprod*n;//Liczba wezłów t
i++; // wynosi n

m=0;
prom_children=∅; //Inicjalizacja zbioru

for(j=1;j<=n;j++){ //obiecujacych potomkow

col[i]=j; //pustym zbiorem

if(promising(i)){ //Okreslenie obiecuj.

m++; //potomkow.
prom_children=prom_children ∪ {j};

}

}
if (m!=0){

j= losowy wybór z prom_children;

col[i]=j;

}

}

return numnodes;

}

Algorytm Monte Carlo można uruchomić wielokrotnie i jako
właściwą wartość wykorzystać średnią z otrzymanych wyników.
Trzeba zauwazyć, że choć prawdopobieństwo uzyskania dobrego
oszacowania jest wysokie przy wielokrotnym uruchomieniu to nigdy
nie mamy gwarancji, że jest to dobre oszacowanie.

Oszacowanie uzyskiwane dla dowolnego przypadku zastosowania
metody Monte Carlo jest prawdziwe tylko dla tego pojedynczego
przypadku. Zdarza się, że gdy mamy dwa różne przypadki dla takiej
samej wartości n, jeden może wymagać sprawdzenia niewielkiej
liczby węzłów, natomiast drugi przejrzenia całego drzewa przestrzeni
stanów.