1
OBLICZENIA RÓWNOLEGŁE
I ROZPROSZONE
Temat 4b:
Deterministyczne problemy
szeregowania zadań, cz.II
Prowadzący:
dr inż. Zbigniew TARAPATA
pok.225A, tel.: 83-95-04
e-mail:
Zbigniew.Tarapata@wat.edu.pl
http://
tarapata.
tarapata.
strefa
strefa
.pl
.pl
/
/
p_obliczenia_rownolegle_i_rozproszone
p_obliczenia_rownolegle_i_rozproszone
/
/
2
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
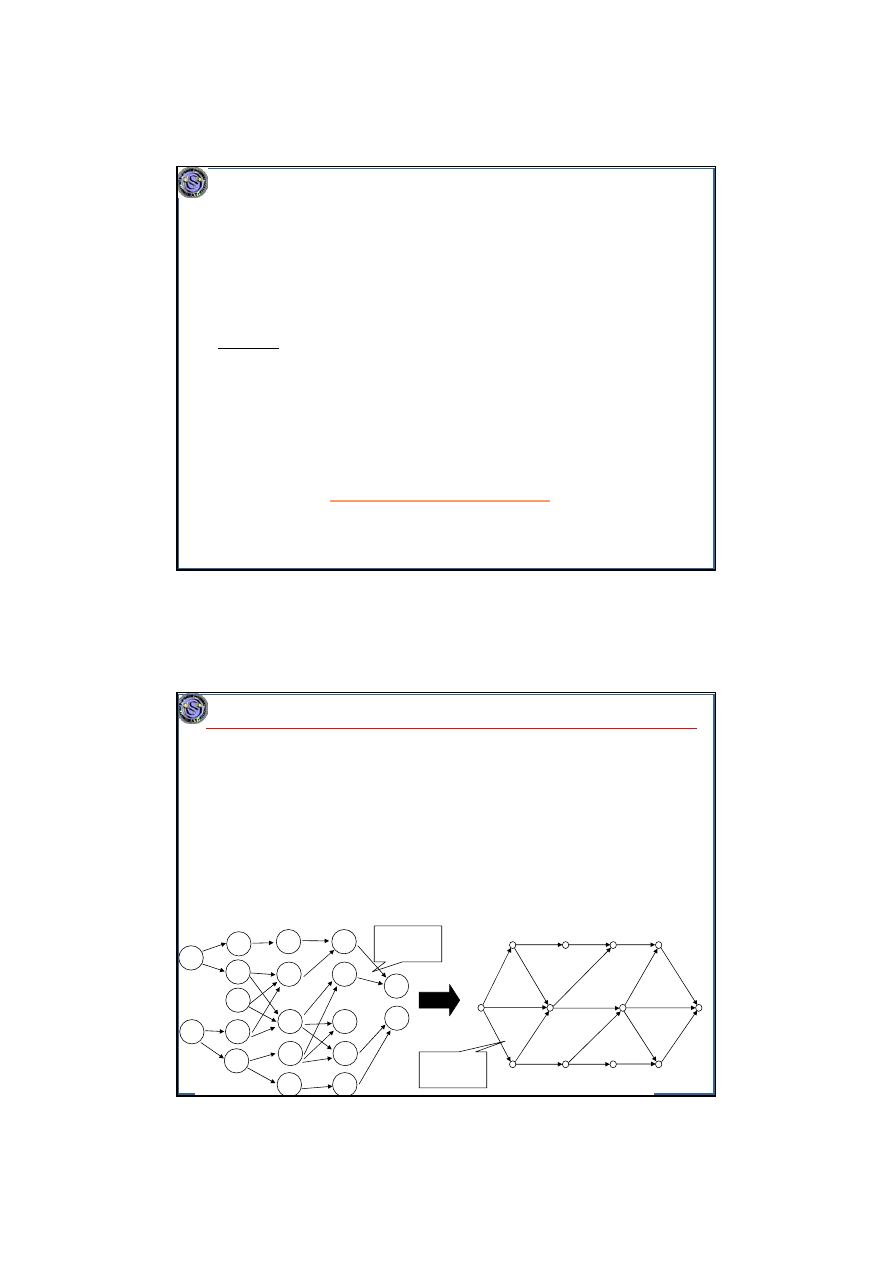
Szeregowanie operacji bezprocesorowych. Metoda ścieżki krytycznej.
Model
–|prec|C
max
operacji o różnych czasach wykonania, z
zależnościami kolejnościowymi, ale nie wymagającymi procesorów.
Celem jest znalezienie najkrótszego możliwego harmonogramu.
Relacja porządku operacji Î
sieć działań
(digraf acykliczny):
• łuki odpowiadają operacjom, ich długości są równe czasom wykonywania,
• przez każdy wierzchołek przechodzi droga z z (źródło) do u (ujście),
• Z
i
≺Z
j
⇔ w sieci istnieje droga z końca łuku Z
i
do początku Z
j
,
• można wprowadzać operacje pozorne – łuki o zerowej długości.
Z
1
,3
Z
2
,8
Z
3
,2
Z
4
,2
Z
5
,4
Z
6
,6
Z
7
,9
Z
9
,1
Z
10
,2
Z
8
,2
Z
11
,1
Z
12
,2
Z
14
,5
Z
15
,9
Z
13
,6
Z
16
,6
Z
17
,2
Z
18
,5
Z
19
,3
Relacja
porządku
A
Z
C
G
U
B
E
H
J
D
F
I
Z
19
,3
Z
13
,6
Z
8
,2
Z
4
,2
Z
2
,8
Z
10
,2
Z
15
,9
Z
17
,2
Z
12
,2
Z
7
,9
Z
18
,5
Z
14
,5
Z
9
,1
Z
5
,4
Z
1
,3
Z
3
,2
Z
6
,6
Z
11
,1
Z
16
,6
Sieć
przedsięwzięcia
2
3
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
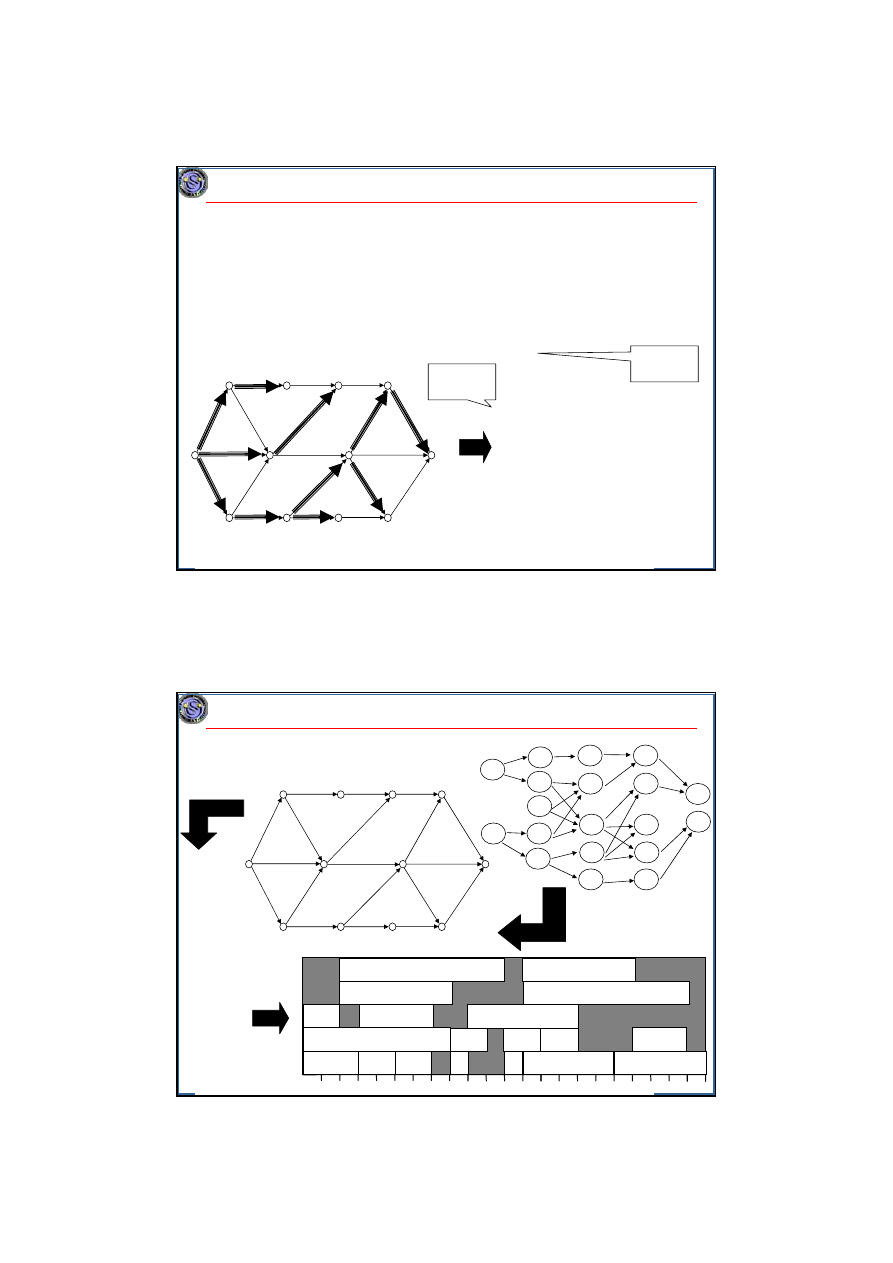
Szeregowanie operacji bezprocesorowych. Metoda ścieżki krytycznej.
Zasada: dla wszystkich wierzchołków v wyznaczamy najdłuższe drogi z z
do v. Ich długość to l(v). Jak to zrobić?
1. numeruj wierzchołki „topologicznie” (brak łuków „pod prąd”),
2. źródłu z nadaj etykietę l(z)=0, a kolejnym wierzchołkom v przypisuj
l(v)=max{l(u)+p
j
: łuk Z
j
prowadzi z u do v},
Wynik: l(v) wierzchołka początkowego Z
j
jest najwcześniejszym
możliwym terminem rozpoczęcia tej operacji. l(u) to termin zakończenia
harmonogramu.
Z:
A:
B:
C:
D:
E:
F:
G:
H:
I:
J:
U:
0
Z:0+3
3
Z:0+2
2
Z:0+8, A:3+4, B:2+6
8
A:3+2
5
B:2+9
11
C:8+1 ,D:5+2
9
C:8+2, E:11+1
12
E:11+2
13
F:9+6, G:12+5
17
G:12+6, H:13+2
18
I:17+5, J:18+3, G:12+9
22
A
Z
C
G
U
B
E
H
J
D
F
I
Z
19
,3
Z
13
,6
Z
8
,2
Z
4
,2
Z
2
,8
Z
10
,2
Z
15
,9
Z
17
,2
Z
12
,2
Z
7
,9
Z
18
,5
Z
14
,5
Z
9
,1
Z
5
,4
Z
1
,3
Z
3
,2
Z
6
,6
Z
11
,1
Z
16
,6
Porządek
topologiczny
Terminy
uruchomienia
4
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Szeregowanie operacji bezprocesorowych. Metoda ścieżki krytycznej.
5
10
15
20
Z
1
Z
4
Z
3
Z
2
Z
6
Z
5
Z
7
Z
9
Z
8
Z
10
Z
11
Z
12
Z
13
Z
14
Z
15
Z
16
Z
17
Z
18
Z
19
Z:
A:
B:
C:
D:
E:
F:
G:
H:
I:
J:
U:
0
3
2
8
5
11
9
12
13
17
18
22
Z
1
,3
Z
2
,8
Z
3
,2
Z
4
,2
Z
5
,4
Z
6
,6
Z
7
,9
Z
9
,1
Z
10
,2
Z
8
,2
Z
11
,1
Z
12
,2
Z
14
,5
Z
15
,9
Z
13
,6
Z
16
,6
Z
17
,2
Z
18
,5
Z
19
,3
A
Z
C
G
U
B
E
H
J
D
F
I
Z
19
,3
Z
13
,6
Z
8
,2
Z
4
,2
Z
2
,8
Z
10
,2
Z
15
,9
Z
17
,2
Z
12
,2
Z
7
,9
Z
18
,5
Z
14
,5
Z
9
,1
Z
5
,4
Z
1
,3
Z
3
,2
Z
6
,6
Z
11
,1
Z
16
,6
3
5
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Szeregowanie operacji bezprocesorowych. Metoda ścieżki krytycznej.
• Algorytm ścieżki krytycznej minimalizuje nie tylko
C
max
, ale
wszystkie zdefiniowane wcześniej funkcje kryterialne.
• Możemy wprowadzić do modelu różne wartości terminów przybycia
r
j
za pomocą łuków pozornych (o długości r
j
, prowadzi z z do początku
łuku Z
j
).
6
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
M
1
M
2
M
3
5
M
1
M
2
M
3
Z
1
5
M
1
M
2
M
3
Z
1
5
Z
2
Z
2
M
1
M
2
M
3
Z
1
5
Z
2
Z
2
Z
3
Z
3
M
1
M
2
M
3
Z
1
5
Z
2
Z
2
Z
4
Z
3
Z
3
M
1
M
2
M
3
Z
1
5
Z
2
Z
2
Z
5
Z
4
Z
3
Z
3
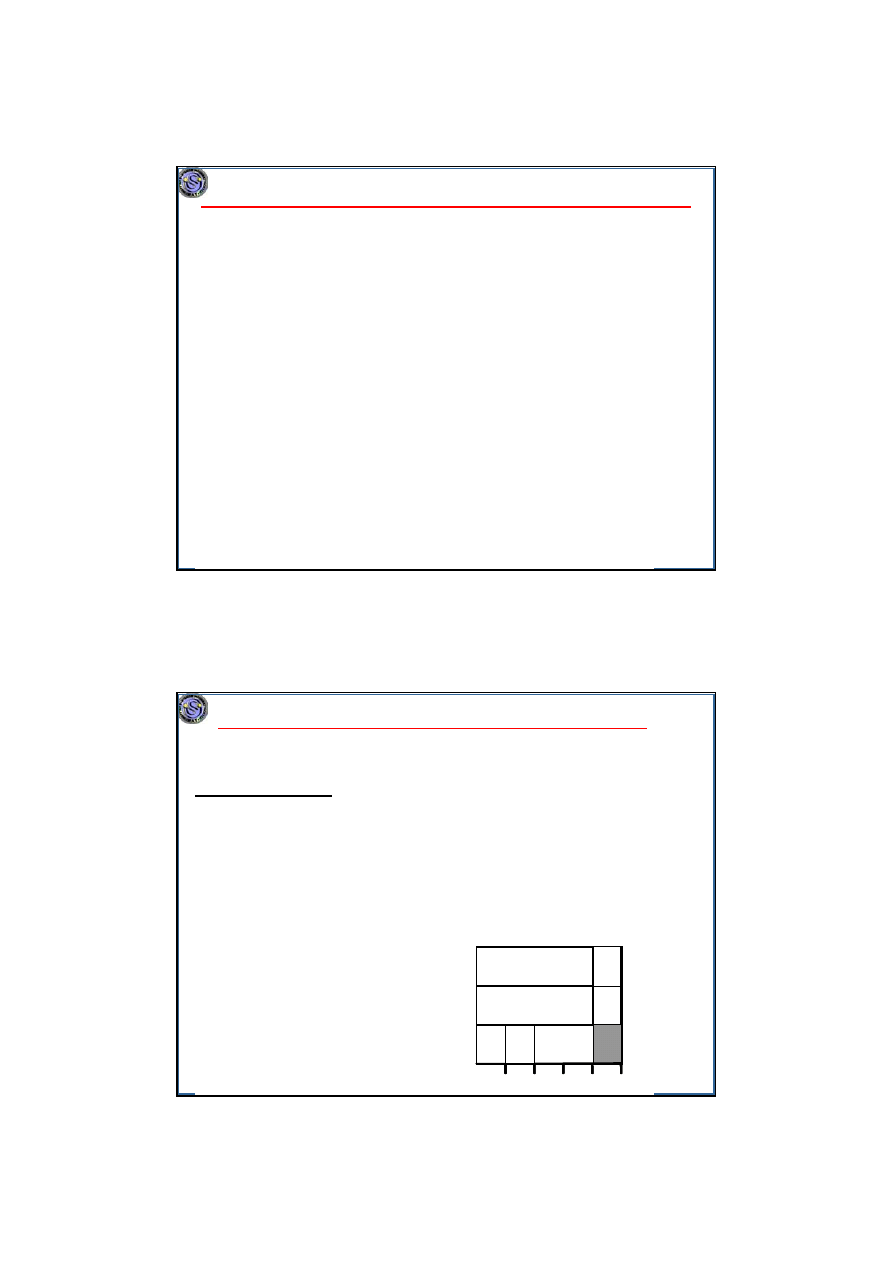
Minimalizacja długości harmonogramu. Maszyny równoległe.
Procesory identyczne, zadania niezależne
Zadania podzielne
P|pmtn|C
max
.
Algorytm
McNaughtona
Złożoność O(n)
1. Wylicz optymalną długość
C*
max
=max{
Σ
j=1,...,n
p
j
/m, max
j=1,...,n
p
j
}
,
2. Szereguj kolejno zadania na maszynie, po osiągnięciu C*
max
przerwij zadanie i (jeśli się nie zakończyło) kontynuuj je na następnym
procesorze począwszy od chwili 0.
Przykład. m=3, n=5, p
1
,...,p
5
=4,5,2,1,2.
Σ
i=1,...,5
p
i
=14, max p
i
=5,
C
max
*=max{14/3,5}=5.
4
7
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
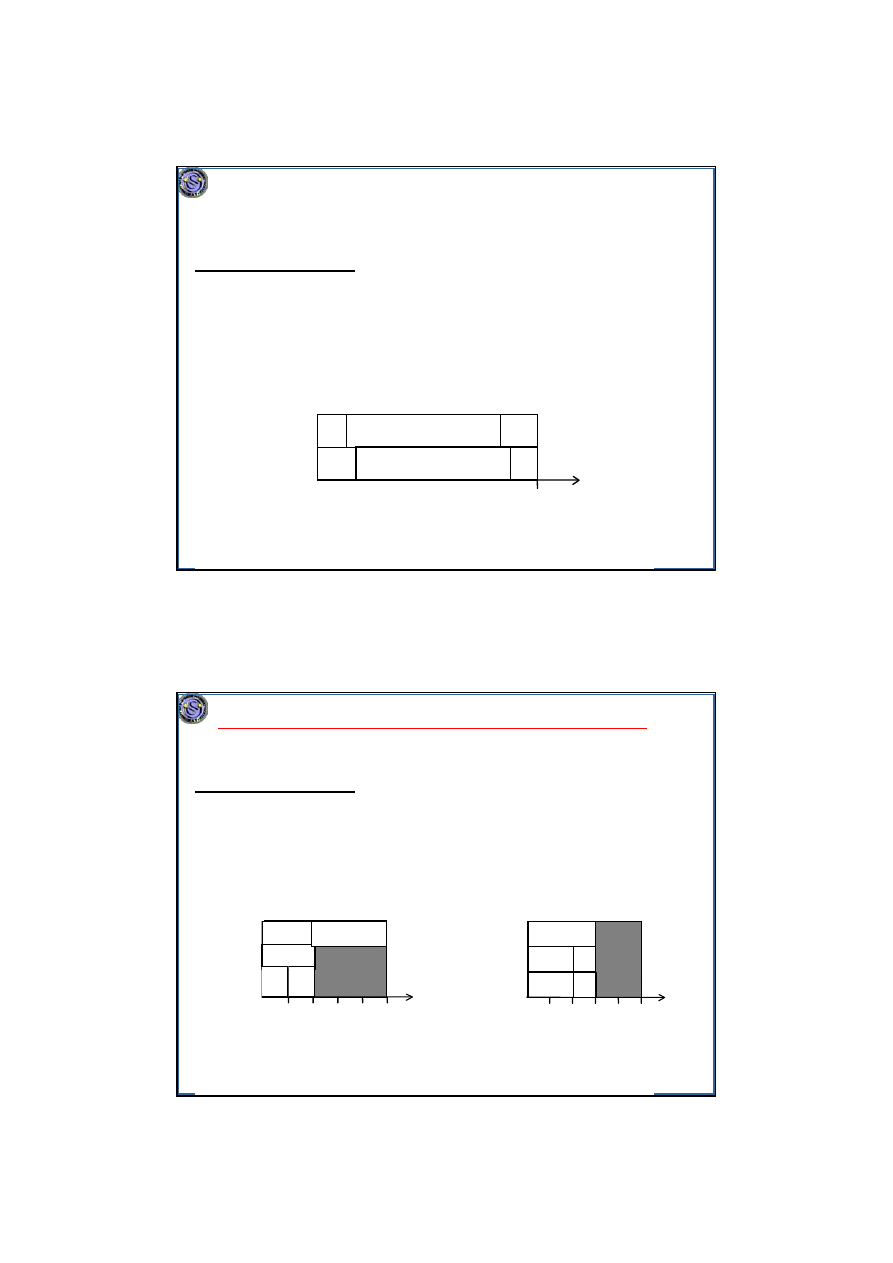
Minimalizacja długości harmonogramu. Maszyny równoległe.
Procesory identyczne, zadania niezależne
Zadania niepodzielne
P||C
max
.
Problem jest NP-trudny już na dwóch maszynach (
P2||C
max
).
Dowód.
Problem podziału
: dany jest ciąg a
1
,...a
n
liczb naturalnych o
S=
Σ
i=1,...,n
a
i
parzystej. Czy istnieje jego podciąg o sumie S/2?
Redukcja PP Î P2||C
max
: bierzemy n zadań o p
j
=a
j
(j=1,...,n), dwie
maszyny, pytamy o istnienie uszeregowania z C
max
≤S/2
.
M
1
M
2
S/2
p
i
...
...
Dokładny algorytm dynamiczny o czasie pracy O(nC
m
), gdzie C
≥C
max
*.
8
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja długości harmonogramu. Maszyny równoległe.
Procesory identyczne, zadania niezależne
Zadania niepodzielne
P||C
max
.
Wielomianowe algorytmy przybliżone.
Szeregowanie listowe
(
List Scheduling LS
):
• Z ustalonego ciągu zadań wybieraj pierwsze wolne (według „listy”),
przypisując je zawsze do zwalniającego się procesora.
Przykład. m=3, n=5, p
1
,...,p
5
=2,2,1,1,3.
M
1
M
2
M
3
5
Uszeregowanie
listowe
Uszeregowanie
optymalne
M
1
M
2
M
3
Z
2
3
Z
1
Z
5
Z
3
Z
4
Dokładność. LS jest 2–przybliżone:
C
max
(LS)
≤(2–m
–1
)C*
max
Z
1
Z
2
Z
3
Z
4
Z
5
5
9
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja długości harmonogramu. Maszyny równoległe.
Procesory identyczne, zadania niezależne
Zadania niepodzielne
P||C
max
.
Wielomianowe algorytmy przybliżone.
Szeregowanie LPT
(
Longest Processing Time
),
SPT
(
Shortest Proc.Time
):
•
Szereguj listowo, przy czym zadania na liście są wstępnie
posortowane według nierosnących (LPT) lub niemalejących (SPT)
czasów wykonania p
i
.
Dokładność. LS jest 4/3–przybliżone:
C
max
(LPT)
≤(4/3–(3m)
–1
)C*
max
.
Procesory dowolne, zadania niezależne
Zadania podzielne
R|pmtn|C
max
Istnieje algorytm wielomianowy - wrócimy do tego ...
Zadania niepodzielne
R||C
max
•
Oczywiście problem jest NP–trudny (uogólnienie
P||C
max
).
• Podproblem
Q|p
i
=1|C
max
można rozwiązać w czasie wielomianowym.
• W praktyce stosuje się LPT.
10
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja długości harmonogramu. Maszyny równoległe.
Procesory identyczne, zadania zależne
Zadania podzielne
P|pmtn,prec|C
max
.
• W ogólności jest to problem NP–trudny.
• Istnieje algorytm O(n
2
) dla
P2|pmtn,prec|C
max
i
P|pmtn,forest|C
max
.
• Pomiędzy optymalnym harmonogramem z przerwami i bez zachodzi:
C*
max
≤(2–m
–1
)C*
max
(pmtn
)
Zadania niepodzielne
P|prec|C
max
.
• Oczywiście problem jest NP–trudny.
• Najbardziej znany podproblem wielomianowy, to
P|p
i
=1,in–forest|C
max
i
P|p
i
=1,out–forest|C
max
(
Algorytm Hu
, złożoność O(n))
• Już przypadek
P|p
i
=1,opositing–forest|C
max
jest NP–trudny.
Algorytm Hu
:
• Redukcja out–forest Î in–forest: odwrócenie relacji prec, a po
uzyskaniu harmonogramu - odwrócenie go,
• in–forest Î in–tree: dodanie “dodatkowego korzenia” dla wszystkich
drzew, a po uzyskaniu harmonogramu usunięcie go.
6
11
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja długości harmonogramu. Maszyny równoległe.
Procesory identyczne, zadania zależne
Zadania niepodzielne
Algorytm Hu
(
P|p
i
=1,in–tree|C
max
):
• Poziom zadania – liczba węzłów na drodze do korzenia.
• Zadanie jest gotowe w chwili t – jeżeli wcześniej wykonane zostały
wszystkie zadania poprzedzające je.
Policz poziomy zadań;
t:=1;
repeat
Wyznacz listę L
t
zadań gotowych w chwili t;
Uporządkuj L
t
według nierosnącego poziomu;
Przypisz m (lub mniej) zadań z początku L
t
do maszyn;
Usuń przypisane zadania z grafu;
t:=t+1;
until uszeregowano wszystkie zadania;
Inaczej: algorytm Hu =
szeregowanie listowe z ograniczeniami
kolejnościowymi +
lista utworzona wg. nierosnącego poziomu.
12
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja długości harmonogramu. Maszyny równoległe.
Procesory identyczne, zadania zależne
Zadania niepodzielne
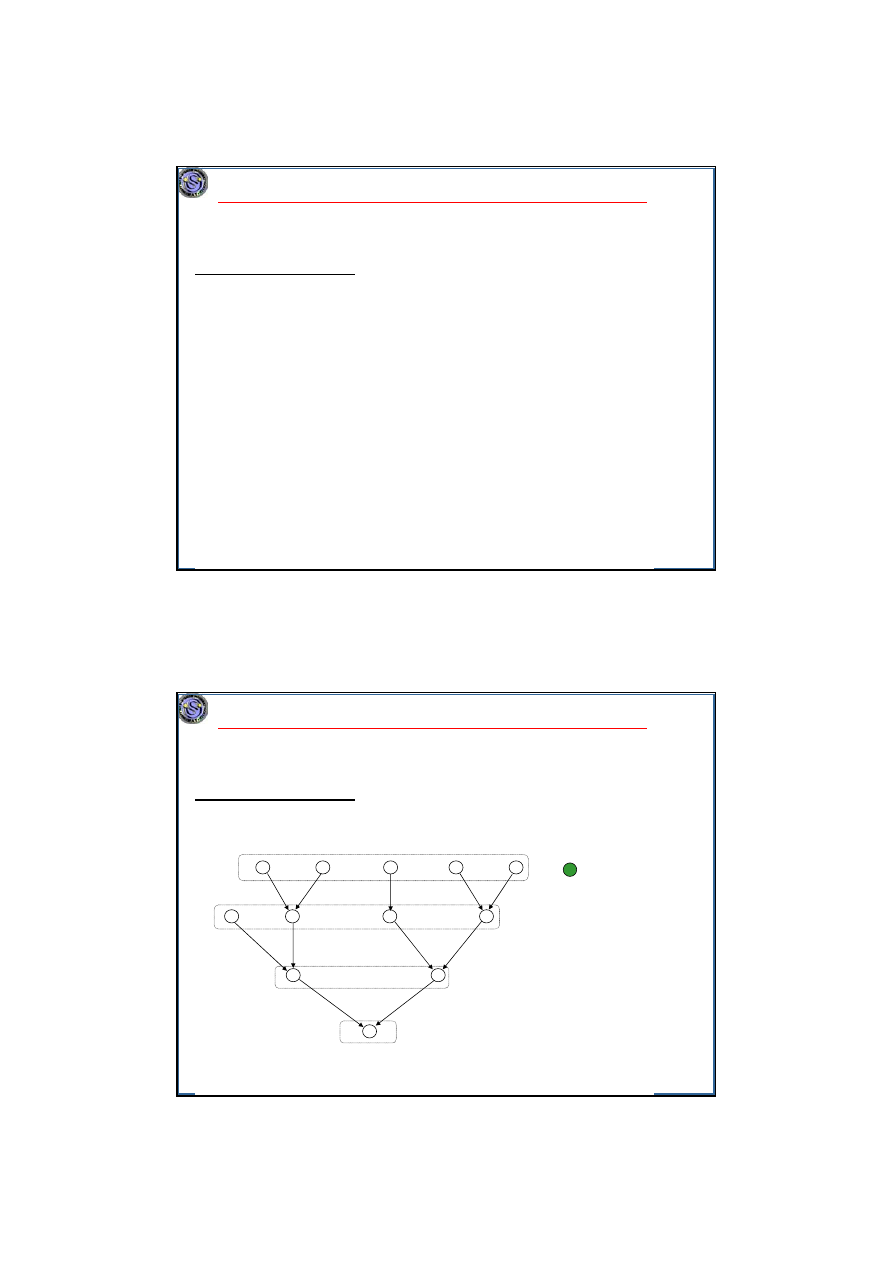
Przykład. Algorytm Hu. n=12, m=3.
T
1
T
2
T
3
T
4
T
5
T
7
T
6
T
10
T
9
T
8
T
11
T
12
1
2
3
4
- zadanie dostępne
(wolne)
7
13
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja długości harmonogramu. Maszyny równoległe.
Procesory identyczne, zadania zależne
Zadania niepodzielne
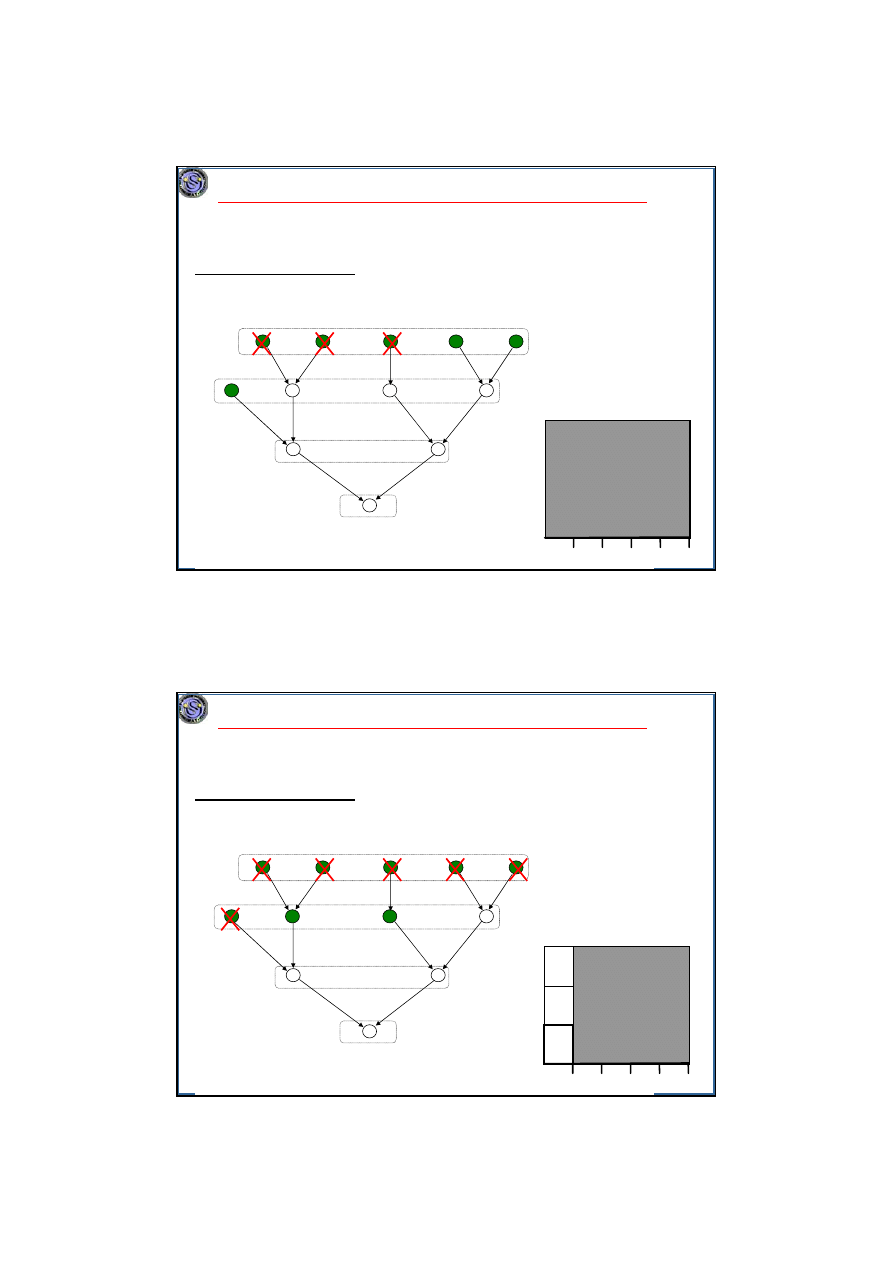
Przykład. Algorytm Hu. n=12, m=3.
T
1
T
2
T
3
T
4
T
5
T
7
T
6
T
10
T
9
T
8
T
11
T
12
1
2
3
4
M
1
M
2
M
3
5
14
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja długości harmonogramu. Maszyny równoległe.
Procesory identyczne, zadania zależne
Zadania niepodzielne
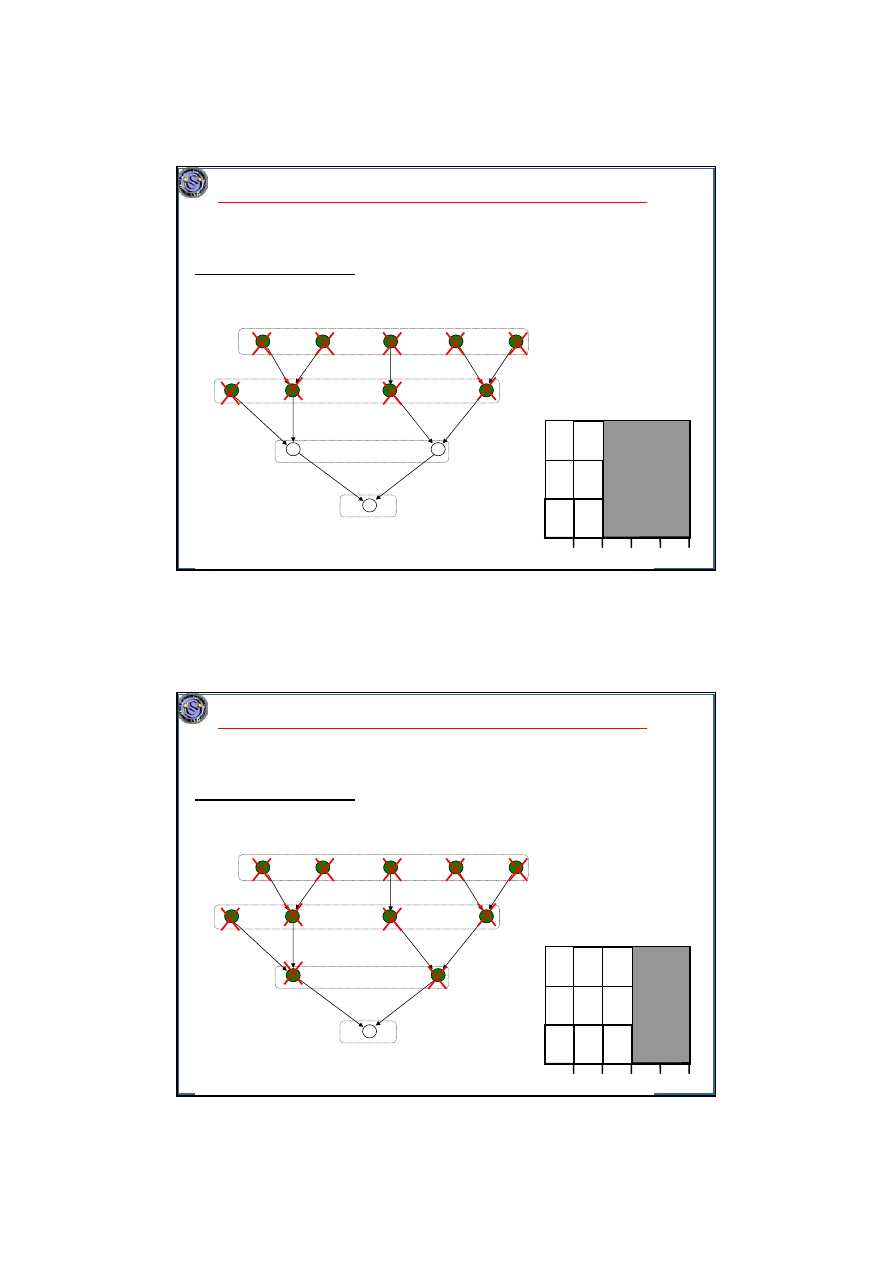
Przykład. Algorytm Hu. n=12, m=3.
T
1
T
2
T
3
T
4
T
5
T
7
T
6
T
10
T
9
T
8
T
11
T
12
1
2
3
4
M
1
M
2
M
3
5
Z
1
Z
3
Z
2
8
15
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja długości harmonogramu. Maszyny równoległe.
Procesory identyczne, zadania zależne
Zadania niepodzielne
Przykład. Algorytm Hu. n=12, m=3.
T
1
T
2
T
3
T
4
T
5
T
7
T
6
T
10
T
9
T
8
T
11
T
12
1
2
3
4
M
1
M
2
M
3
5
Z
1
Z
6
Z
3
Z
2
Z
4
Z
5
16
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja długości harmonogramu. Maszyny równoległe.
Procesory identyczne, zadania zależne
Zadania niepodzielne
Przykład. Algorytm Hu. n=12, m=3.
T
1
T
2
T
3
T
4
T
5
T
7
T
6
T
10
T
9
T
8
T
11
T
12
1
2
3
4
M
1
M
2
M
3
5
Z
1
Z
6
Z
3
Z
2
Z
4
Z
5
Z
9
Z
7
Z
8
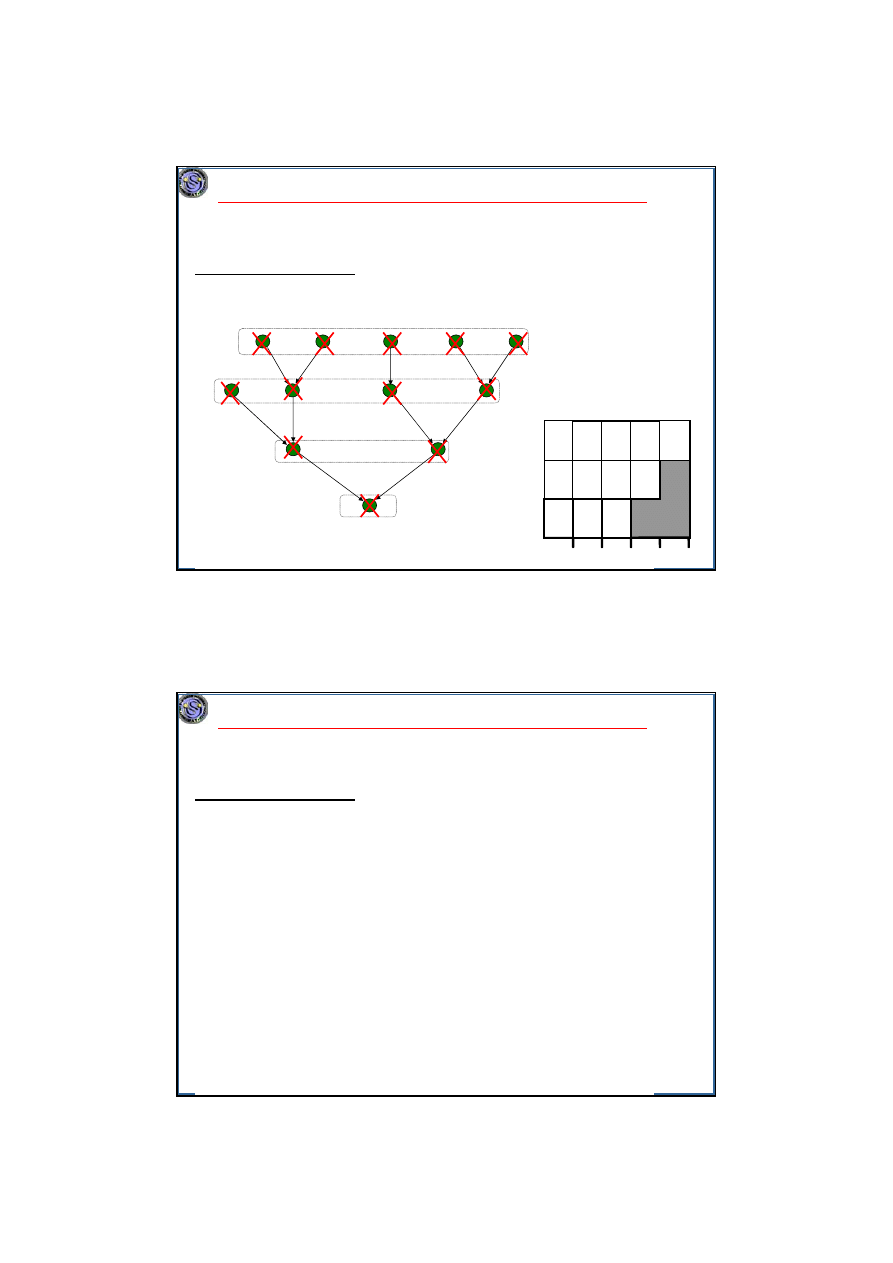
9
17
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja długości harmonogramu. Maszyny równoległe.
Procesory identyczne, zadania zależne
Zadania niepodzielne
Przykład. Algorytm Hu. n=12, m=3.
T
1
T
2
T
3
T
4
T
5
T
7
T
6
T
10
T
9
T
8
T
11
T
12
1
2
3
4
M
1
M
2
M
3
5
Z
1
Z
6
Z
3
Z
2
Z
4
Z
5
Z
9
Z
7
Z
8
Z
10
Z
11
M
1
M
2
M
3
5
Z
1
Z
6
Z
3
Z
2
Z
4
Z
5
Z
9
Z
7
Z
8
Z
10
Z
11
Z
12
18
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja długości harmonogramu. Maszyny równoległe.
Procesory identyczne, zadania zależne
Zadania niepodzielne
Dla ogólnego
P|prec|C
max
można stosować heurystykę LS. Kolejność
zadań na liście (priorytety) ustala się różnymi metodami. Mogą się
pojawiać anomalie polegające na wydłużaniu się harmonogramu przy:
• wzroście liczby maszyn,
• zmniejszaniu czasu wykonania zadań,
• zmniejszaniu relacji prec,
• zmianie kolejności na liście.
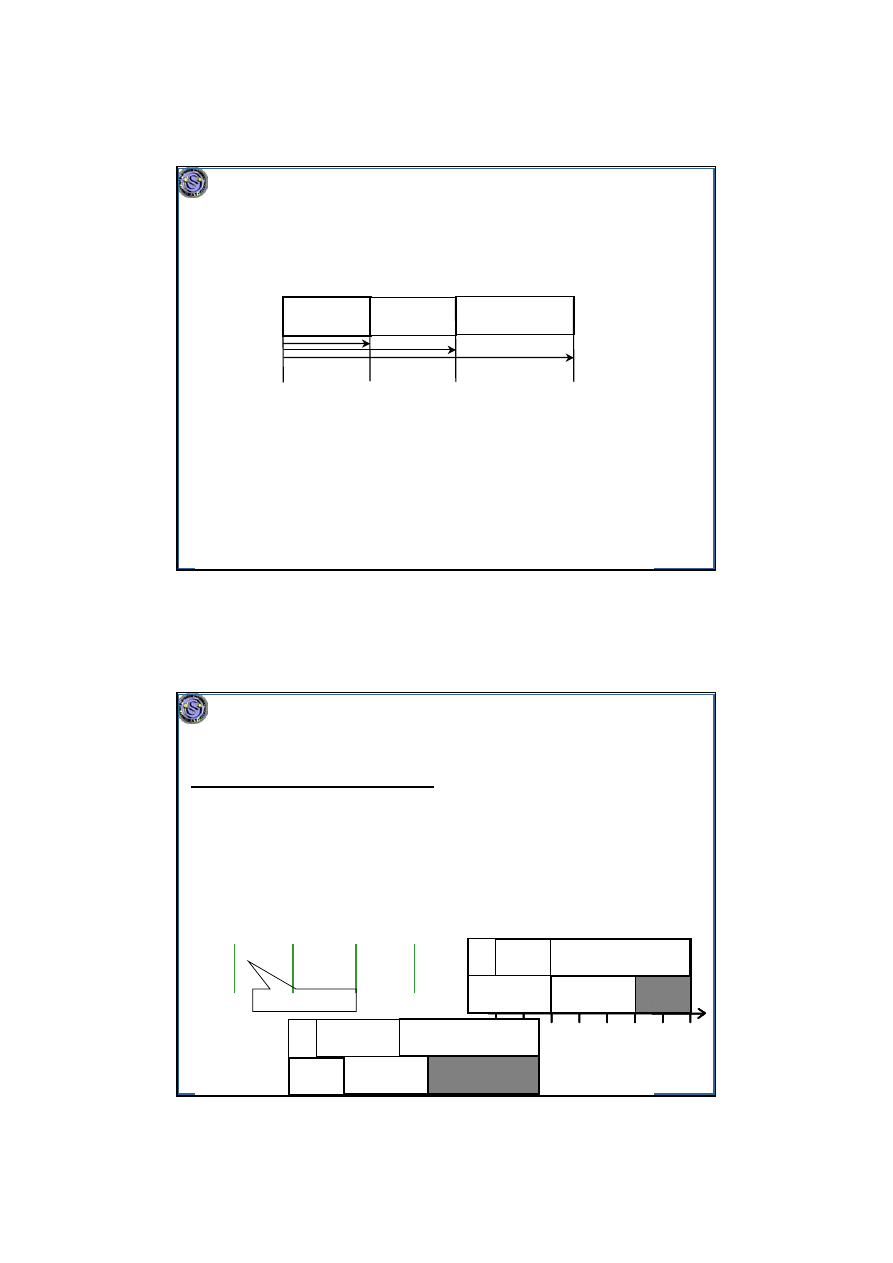
10
19
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja średniego czasu przepływu na maszynach równoległych
Procesory identyczne, zadania niezależne
Wnioski.
• długość pierwszego zadania jest mnożona przez największy
współczynnik, dla kolejnych zadań współczynniki maleją,
• minimalizując
ΣC
j
powinniśmy umieszczać krótkie zadania na początku
(są mnożone przez największe współczynniki),
• optymalne uszeregowanie jest zgodne z regułą
SPT
(
Shortest Processing
Times
) – zadania na maszynach są podejmowane w kolejności
niemalejących czasów wykonania,
•
ale jak znaleźć optymalne przypisanie zadań do procesorów?
Własność: zadanie Z
j
na maszynie M
i
umieszczone na k–tej pozycji od
końca dodaje do kryterium
ΣC
j
wartość kp
j
(lub kp
ij
dla maszyn
R|
).
M
Z
a
Z
c
Z
b
×3
×2
×1
20
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja średniego czasu przepływu na maszynach równoległych
Procesory identyczne, zadania niezależne
Zadania podzielne i niepodzielne
Przypadki
P||
ΣC
i
i podzielnych
P|pmtn|
ΣC
i
można rozpatrywać razem
(optymalny harmonogram podzielny nie musi dzielić zadań).
Algorytm optymalny
O(nlog n):
1. Przyjmij, że liczba zadań dzieli się przez m (ew. wprowadź zadania puste),
2. Uporządkuj je według SPT,
3. Przypisuj kolejne m–tki zadań w sposób dowolny do różnych maszyn.
Przykład. m=2, n=5, p
1
,...,p
5
=2,5,3,1,3.
SPT:
Z
4
Z
1
Z
3
Z
5
Z
2
p
i
=
1 2 3 3 5
M
1
M
2
8
M
1
M
2
8
Z
4
M
1
M
2
8
Z
4
Z
3
Z
1
M
1
M
2
8
Z
4
Z
3
Z
1
Z
5
Z
2
M
1
M
2
Z
4
Z
3
Z
1
Z
5
Z
2
Można
i tak:
9
ΣC
j
*=21
Z
0
0
Zadanie puste
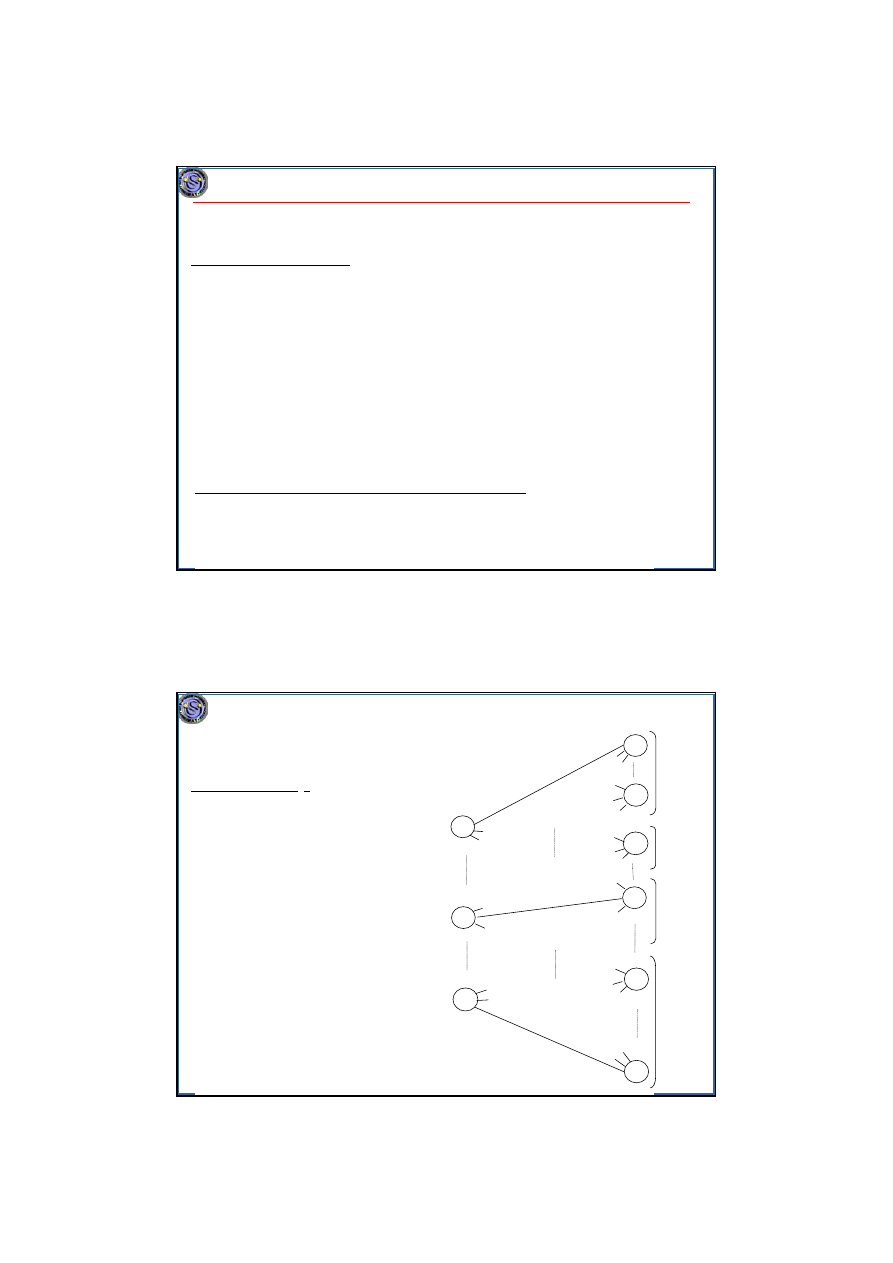
11
21
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja średniego czasu przepływu na maszynach równoległych
Procesory identyczne, zadania niezależne
Zadania niepodzielne
Już wersja ważona
P2||
Σw
j
C
j
jest NP-trudna
.
Dowód. Jak w P2||C
max
. Redukcja PP Î P2||
Σw
i
C
i
: bierzemy n zadań o
p
j
= w
j
=a
j
(j=1,...,n), dwie maszyny. Wyznacz liczbę C(a
1
,...,a
n
) taką, że
istnieje uszeregowanie o
Σw
j
C
j
≤C(a
1
,...,a
n
)
⇔ C
max
*
=
Σ
i=1,...,n
a
i
/2
(ćwiczenie).
Próbą pogodzenia kryteriów
C
max
i
ΣC
i
jest
algorytm RPT
:
1. Zastosuj szeregowanie LPT.
2. Na każdej maszynie posortuj zadania według SPT.
Dokładność:
1
≤ΣC
i
(RPT)
/
ΣC
i
*
≤m
(zwykle jest lepsza)
Procesory identyczne, zadania zależne
•
Już
P2|prec,p
j
=1|
ΣC
i
,
P2|chains|
ΣC
i
i
P2|chains,pmtn|
ΣC
i
są NP–trudne.
• Dla
P|out–tree,p
j
=1|
ΣC
i
znany jest wielomianowy algorytm oparty na
regule Hu.
22
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja średniego czasu przepływu na maszynach równoległych
Procesory dowolne, zadania niezależne
Algorytm O(n
3
) dla
R||
ΣC
i
bazuje na problemie skojarzeń
w grafach.
Graf dwudzielny z
krawędziami obciążonymi
wagami:
• W partycji V
1
zadania Z
1
,...,Z
n
.
• W partycji V
2
każdy procesor n
razy:
k
M
i
, i=1...m, k=1...n.
• Krawędź z Z
j
do
k
M
i
ma wagę
kp
ij
– oznacza ona zadanie Z
j
na
maszynie M
i
, pozycja k-ta od
końca.
kp
ij
Z
1
Z
j
Z
n
1
M
1
1
M
m
2
M
1
n
M
m
n
M
1
k
M
i
2
k
n
1
Szukamy najlżejszego skojarzenia o
n krawędziach. Przedstawia ono
szukany harmonogram.
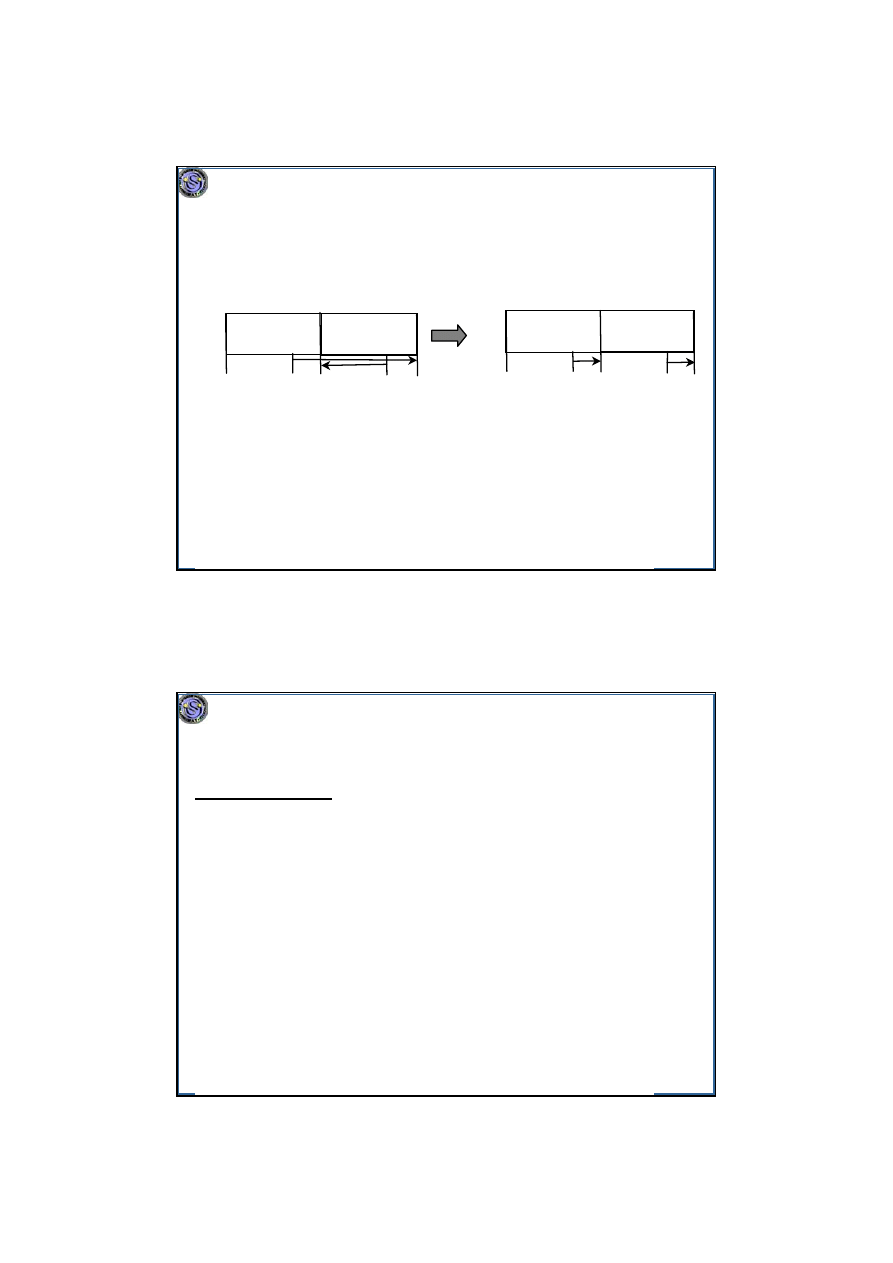
12
23
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja maksymalnego opóźnienia na maszynach równoległych
Własności:
•
kryterium L
max
jest uogólnieniem C
max
, zagadnienia NP–trudne dla C
max
pozostaną takie w przypadku L
max
,
• mając do wykonania wiele prac z różnymi wymaganymi terminami
zakończenia spóźnimy się „najmniej” zaczynając zawsze od
„najpilniejszej” pracy,
• to samo innymi słowy: w różnych wariantach stosujemy
regułę EDD
(
Earliest Due Date
) – wybieraj zadania Z
j
w kolejności niemalejących
wymaganych terminów zakończenia d
j
,
• problem zadań niepodzielnych na jednej maszynie (
1||L
max
) rozwiązuje
właśnie szeregowanie według EDD.
M
Z
a
Z
b
d
a
d
b
M
Z
a
Z
b
d
a
d
b
24
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja maksymalnego opóźnienia na maszynach równoległych
Procesory identyczne, zadania niezależne
Zadania podzielne
Jedna maszyna:
Algorytm Liu
O(n
2
), oparty na regule EDD,
działający nawet przy
1|r
i
,pmtn|L
max
:
1. Spośród dostępnych zadań przydziel maszynę temu, które ma
najmniejszy wymagany termin zakończenia,
2. Jeśli zadanie zostało zakończone, lub przybyło nowe – wróć do 1
(w drugim przypadku przerywamy zadanie).
Więcej maszyn (
P|r
i
,pmtn|L
max
). Również algorytm wielomianowy:
korzystamy z podprocedury rozwiązującej wersję z “twardymi”
terminami zakończenia
P|r
i
,C
i
≤d
i
,pmtn|–
, szukamy optymalnego
L
max
metodą połowienia.
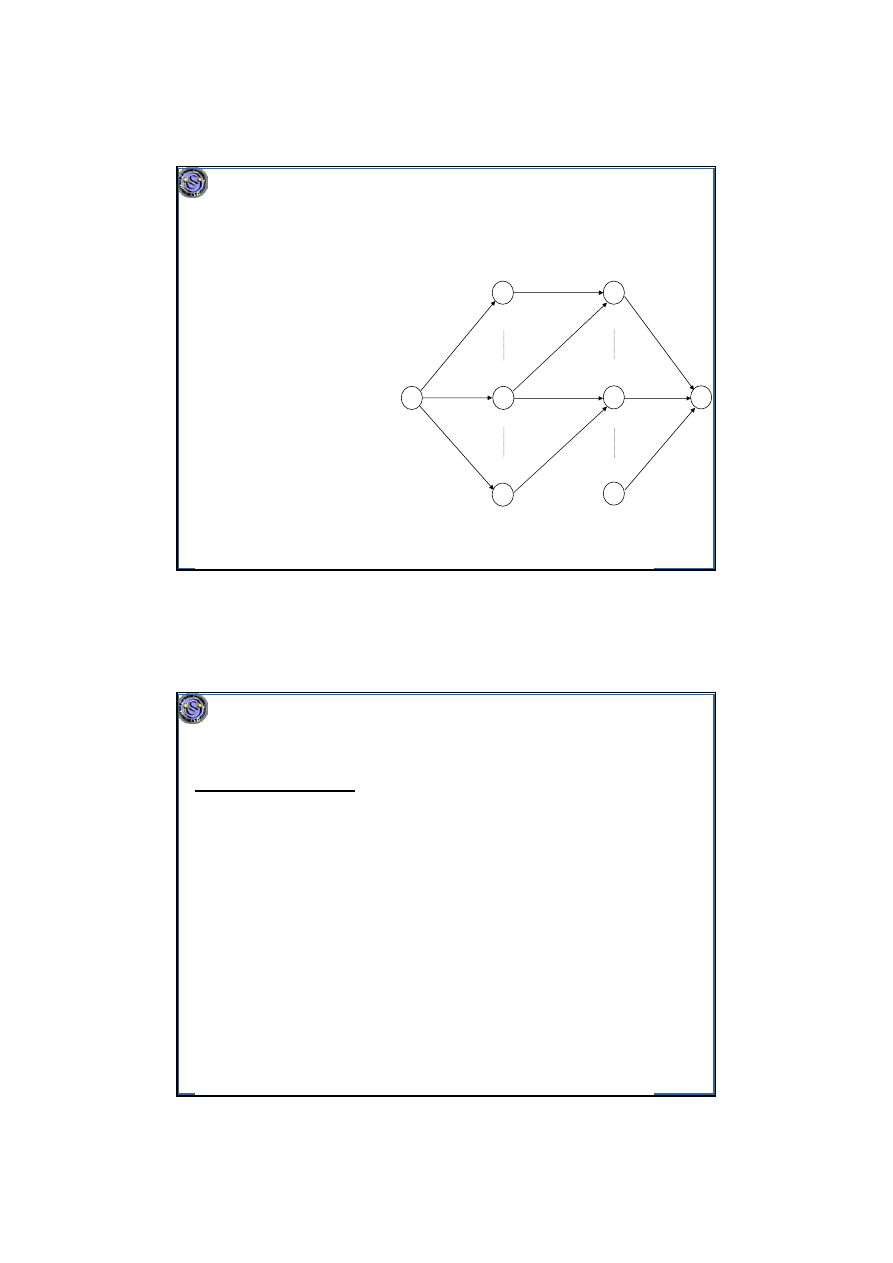
13
25
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja maksymalnego opóźnienia na maszynach równoległych
P|r
i
,C
i
≤d
i
,pmtn|–
sprowadzamy do problemu przepływu. Ustawiamy
wszystkie r
i
i d
i
w ciąg e
0
<e
1
<...<e
k
.
m(e
1
-e
0
)
m(e
i
-e
i-1
)
Z
U
w
1
w
i
w
k
Z
1
Z
j
Z
n
m(e
k
-e
k-1
)
p
1
p
j
p
n
e
1
-e
0
e
i
-e
i-1
Tworzymy sieć:
• Ze źródła wychodzi k łuków o
przepustowości m(e
i
–e
i–1
) do
wierzchołków w
i
, i=1,...,k.
• Do ujścia wchodzą łuki o
przepustowości p
i
z
wierzchołków Z
i
, i=1,...,n.
• Między w
i
a Z
j
biegnie łuk o
przepustowości e
i
–e
i–1
, jeżeli
zachodzi [e
i–1
,e
i
]
⊂[r
j
,d
j
].
Uszeregowanie istnieje
⇔ istnieje przepływ o objętości Σ
i=1,...,n
p
i
(można
rozdysponować moce obliczeniowe procesorów do zadań w odpowiednich
odcinkach czasu, tak by wykonać wszystkie).
26
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja maksymalnego opóźnienia na maszynach równoległych
Niektóre przypadki NP-trudne:
P2||L
max
, 1|r
j
|L
max
.
Zadania niezależne
Zadania niepodzielne
Przypadki wielomianowe:
• dla zadań jednostkowych
P|p
j
=1,r
j
|L
max
.
• podobnie dla maszyn jednorodnych
Q|p
j
=1|L
max
(redukcja do
programowania liniowego),
• dla jednej maszyny rozwiązanie optymalne
1||L
max
uzyskamy
szeregując według EDD (to już było ...).
14
27
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja maksymalnego opóźnienia na maszynach równoległych
Dla jednej maszyny
1|pmtn,prec,r
j
|L
max
zmodyfikowany algorytm Liu
O(n
2
):
1. określ
zmodyfikowane terminy zakończenia
zadań:
d
j
*=min{d
j
, min{d
i
:Z
j
≺Z
i
}}
2. szereguj według EDD dla nowych d
j
* z wywłaszczaniem zadania, gdy
pojawia się nowe, wolne, z mniejszym zmodyfikowanym terminem
zakończenia,
3. powtarzaj 2 aż do uszeregowania wszystkich zadań.
Zadania zależne
Zadania podzielne
• Inne przypadki wielomianowe:
P|pmtn,in–tree|L
max
, Q2|pmtn,prec,r
j
|L
max
.
• Stosuje się też algorytmy pseudowielomianowe.
28
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja maksymalnego opóźnienia na maszynach równoległych
• Już
P|p
j
=1,out–tree|L
max
jest NP–trudny.
•
P|p
j
=1,in–tree|L
max
rozwiązuje
algorytm Bruckera
O(nlog n):
Zadania zależne
Zadania niepodzielne
next(j) = bezpośredni następnik zadania Z
j
.
1. wylicz zmodyfikowane terminy zakończenia zadań:
dla korzenia
d
root
*=1–d
root
i dla pozostałych
d
k
*=max{1+d
next(k)
*,1–d
k
}
,
2. szereguj zadania dostępne podobnie jak w algorytmie Hu, ale remisy
rozstrzygaj wybierając zadania według nierosnących
zmodyfikowanych terminów zakończenia, a nie według poziomów w
drzewie.
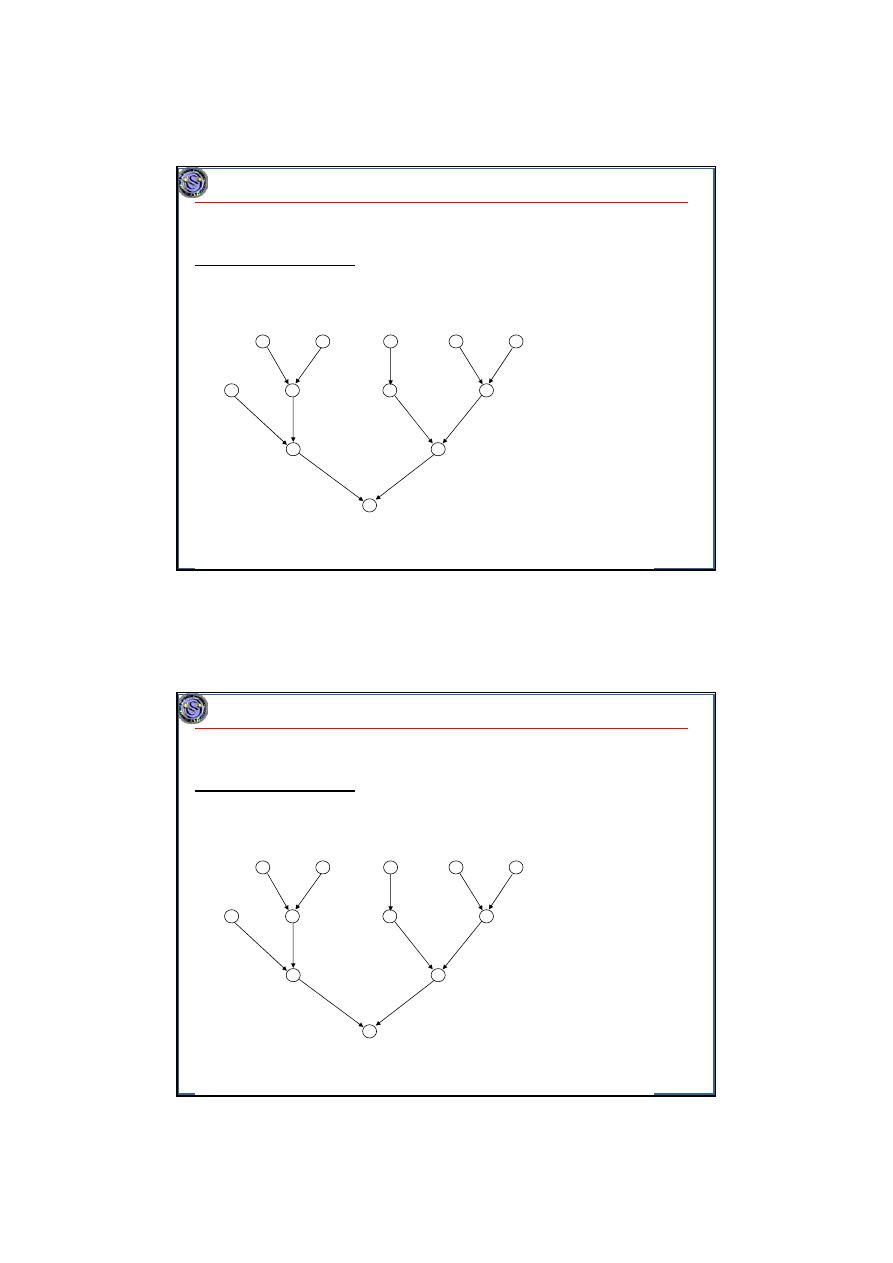
15
29
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja maksymalnego opóźnienia na maszynach równoległych
Zadania zależne
Zadania niepodzielne
Przykład. Algorytm Bruckera, n=12, m=3, terminy zakończenia d
k
w
kółkach.
T
1
T
2
T
3
T
4
T
5
T
7
T
6
T
10
T
9
T
8
T
11
T
12
7
6
3
1
5
3
1
4
6
4
2
3
-6
-5
,-5
-2
,-5
0
,-4
-4
,-4
-2,
-1
0
,-1
-3
,-3
-5,
-3
-3,
0
-1,
1
-2,
1
30
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja maksymalnego opóźnienia na maszynach równoległych
Zadania zależne
Zadania niepodzielne
Przykład. Algorytm Bruckera, n=12, m=3, terminy zakończenia w kółkach.
T
1
T
2
T
3
T
4
T
5
T
7
T
6
T
10
T
9
T
8
T
11
T
12
7
6
3
1
5
3
1
4
6
4
2
3
-6
-5
-2
0
-4
-1
0
-3
-3
0
1
1
16
31
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
T
1
T
2
T
3
T
4
T
5
T
7
T
6
T
10
T
9
T
8
T
11
T
12
M
1
M
2
M
3
6
Minimalizacja maksymalnego opóźnienia na maszynach równoległych
Zadania zależne
Zadania niepodzielne
Przykład. Algorytm Bruckera, n=12, m=3, terminy zakończenia w kółkach.
-6
-5
-2
0
-4
-1
0
-3
-3
0
1
1
32
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
T
1
T
2
T
3
T
4
T
5
T
7
T
6
T
10
T
9
T
8
T
11
T
12
M
1
M
2
M
3
6
Z
3
Z
5
Z
4
-6
-5
-2
0
-4
-1
0
-3
-3
0
1
1
Minimalizacja maksymalnego opóźnienia na maszynach równoległych
Zadania zależne
Zadania niepodzielne
Przykład. Algorytm Bruckera, n=12, m=3, terminy zakończenia w kółkach.
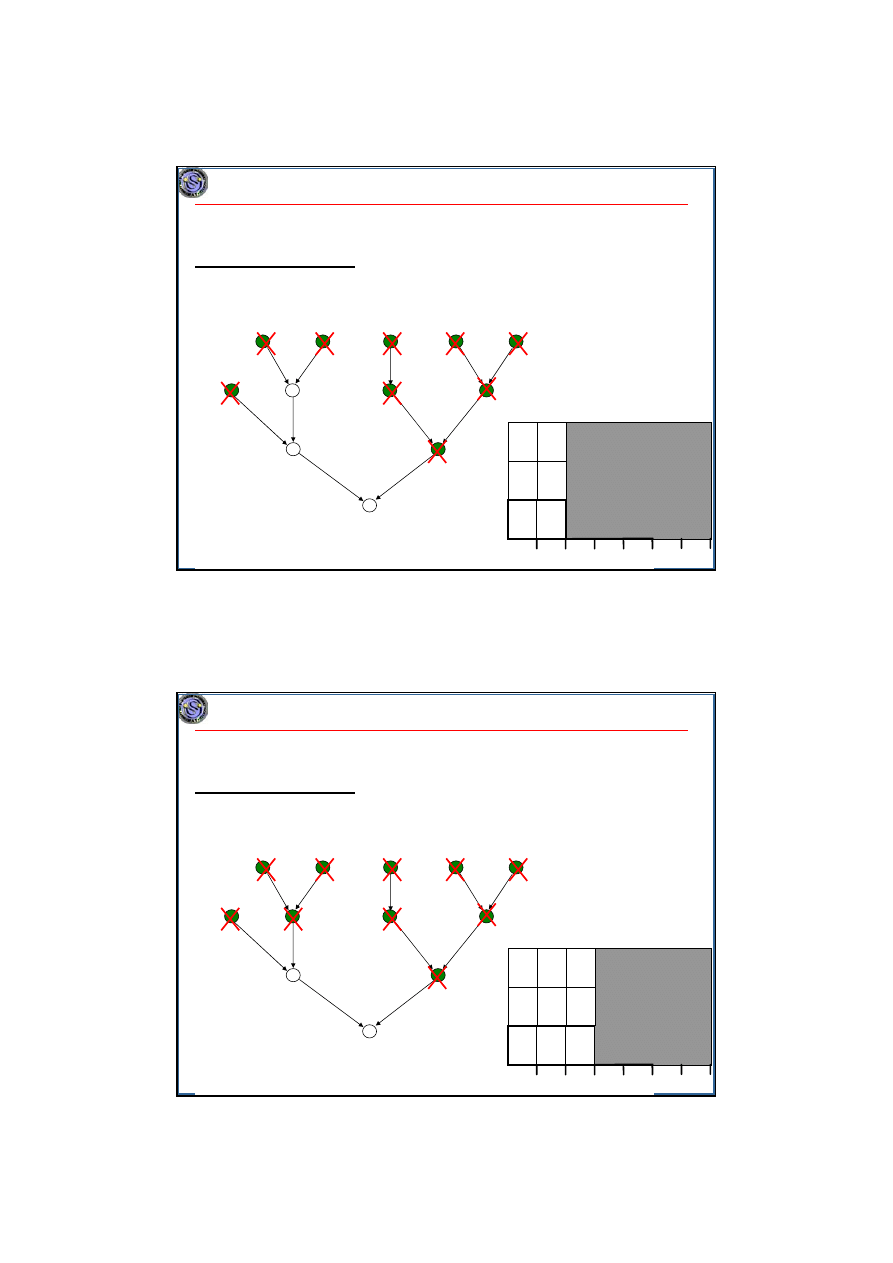
17
33
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
T
1
T
2
T
3
T
4
T
5
T
7
T
6
T
10
T
9
T
8
T
11
T
12
M
1
M
2
M
3
6
Z
3
Z
5
Z
4
Z
6
Z
9
Z
8
-6
-5
-2
0
-4
-1
0
-3
-3
0
1
1
Minimalizacja maksymalnego opóźnienia na maszynach równoległych
Zadania zależne
Zadania niepodzielne
Przykład. Algorytm Bruckera, n=12, m=3, terminy zakończenia w kółkach.
34
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
T
1
T
2
T
3
T
4
T
5
T
7
T
6
T
10
T
9
T
8
T
11
T
12
M
1
M
2
M
3
6
Z
3
Z
5
Z
4
Z
6
Z
9
Z
8
Z
1
Z
11
Z
2
-6
-5
-2
0
-4
-1
0
-3
-3
0
1
1
Minimalizacja maksymalnego opóźnienia na maszynach równoległych
Zadania zależne
Zadania niepodzielne
Przykład. Algorytm Bruckera, n=12, m=3, terminy zakończenia w kółkach.
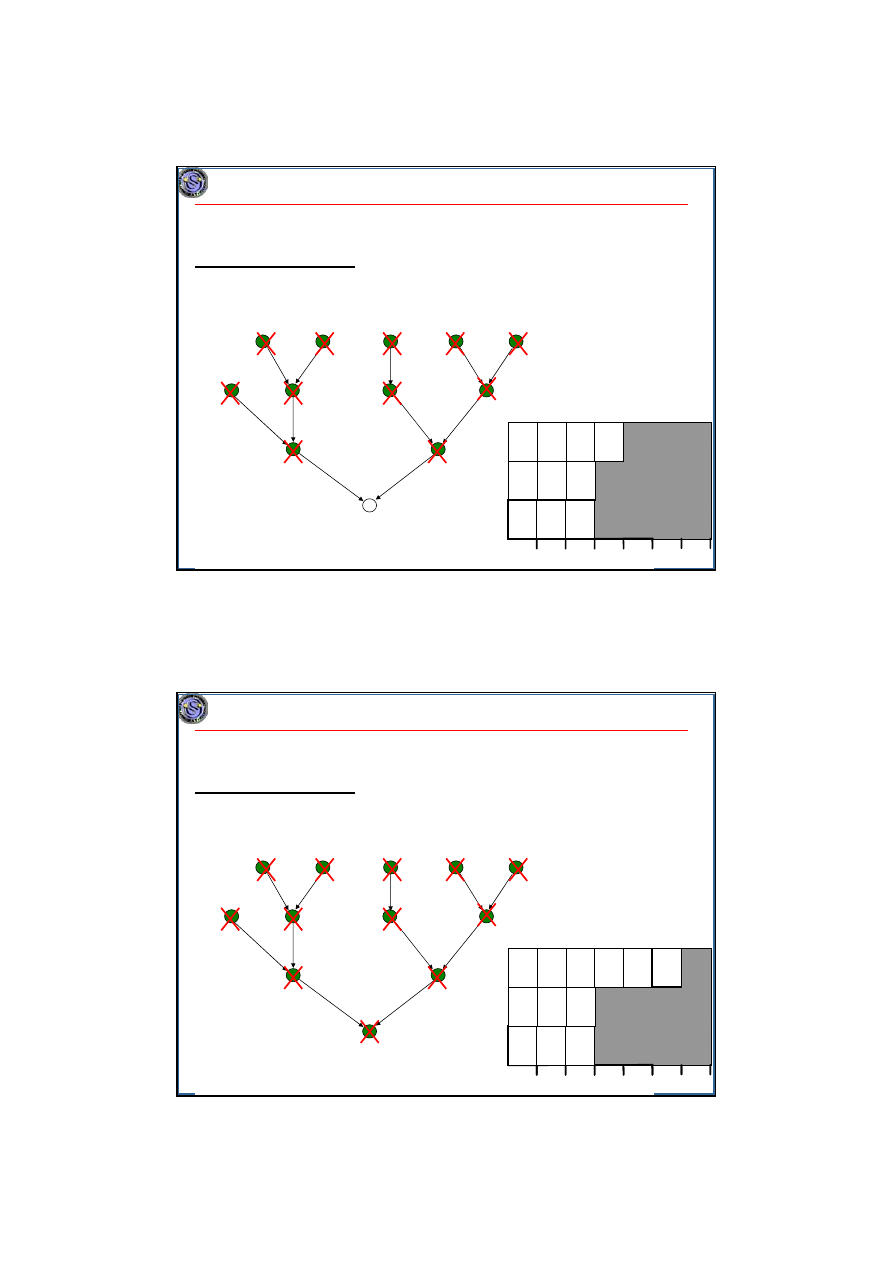
18
35
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
T
1
T
2
T
3
T
4
T
5
T
7
T
6
T
10
T
9
T
8
T
11
T
12
M
1
M
2
M
3
6
Z
3
Z
5
Z
4
Z
6
Z
9
Z
8
Z
1
Z
11
Z
2
Z
7
-6
-5
-2
0
-4
-1
0
-3
-3
0
1
1
Minimalizacja maksymalnego opóźnienia na maszynach równoległych
Zadania zależne
Zadania niepodzielne
Przykład. Algorytm Bruckera, n=12, m=3, terminy zakończenia w kółkach.
36
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
T
1
T
2
T
3
T
4
T
5
T
7
T
6
T
10
T
9
T
8
T
11
T
12
M
1
M
2
M
3
6
Z
3
Z
5
Z
4
Z
6
Z
9
Z
8
Z
1
Z
11
Z
2
Z
7
Z
10
-6
-5
-2
0
-4
-1
0
-3
-3
0
1
1
Minimalizacja maksymalnego opóźnienia na maszynach równoległych
Zadania zależne
Zadania niepodzielne
Przykład. Algorytm Bruckera, n=12, m=3, terminy zakończenia w kółkach.
M
1
M
2
M
3
6
Z
3
Z
5
Z
4
Z
6
Z
9
Z
8
Z
1
Z
11
Z
2
Z
7
Z
10
Z
12
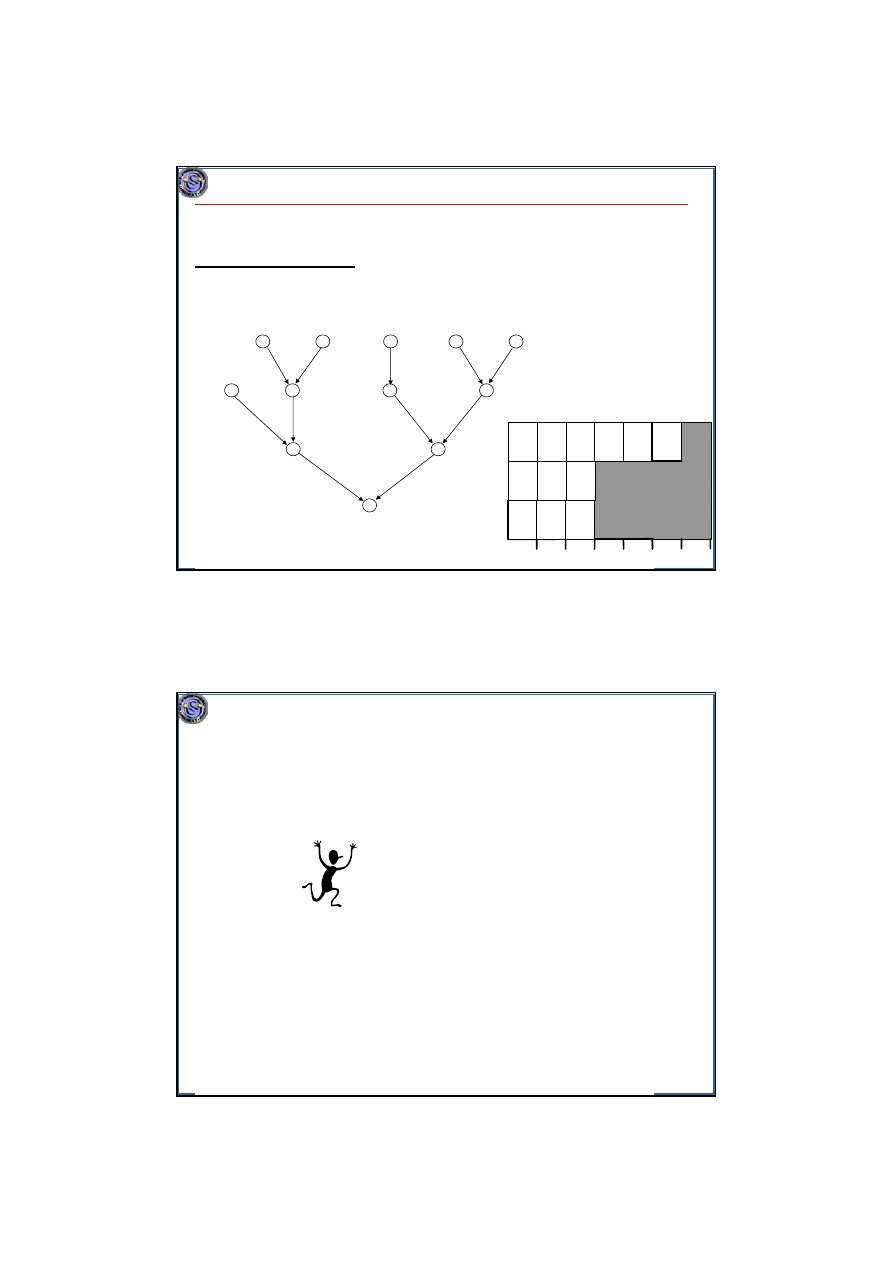
19
37
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Minimalizacja maksymalnego opóźnienia na maszynach równoległych
Zadania zależne
Zadania niepodzielne
Przykład. Algorytm Bruckera, n=12, m=3, terminy zakończenia w kółkach.
T
1
T
2
T
3
T
4
T
5
T
7
T
6
T
10
T
9
T
8
T
11
T
12
7
6
3
1
5
3
1
4
6
4
2
3
M
1
M
2
M
3
6
Z
3
Z
5
Z
4
Z
6
Z
9
Z
8
Z
1
Z
11
Z
2
Z
7
Z
10
Z
12
-1
-1
0
L
max
*=1
-1
-1
1
-1
-3
-3
-1
-2
Opóźnienia:
38
Z.Tarapata, Obliczenia równoległe i rozproszone, wykład nr 4b,
http://tarapata.strefa.pl/p_obliczenia_rownolegle_i_rozproszone/
Dziękuję za uwagę
Wyszukiwarka
Podobne podstrony:
or wyklad 4a id 339028 Nieznany
AiSD Wyklad4 dzienne id 53497 Nieznany (2)
3 Wyklad OiSE id 33284 Nieznany
Materialy do wykladu nr 5 id 28 Nieznany
Finanse Wyklady FiR id 172193 Nieznany
AiSD Wyklad9 dzienne id 53501 Nieznany
Folie wyklad2 Krakow id 286699 Nieznany
OP wyklad nr 3 id 335762 Nieznany
prc wyklad zagad 5 id 388963 Nieznany
hydrologia wyklad 06 id 207845 Nieznany
hydrologia wyklad 05 id 207839 Nieznany
F II wyklad 11 id 167234 Nieznany
BHP Wyklad 10 id 84576 Nieznany (2)
AiSD Wyklad11 dzienne id 53494 Nieznany
elektro wyklad 03b id 157928 Nieznany
fcs wyklad comment 2 2 id 16907 Nieznany
więcej podobnych podstron