ANALIZA ALGORYTMÓW
Analiza algorytmów polega między innymi na odpowiedzi na
pytania:
1) Czy problem może być rozwiązany na komputerze w
dostępnym czasie i pamięci?
2) Który ze znanych algorytmów należy zastosować w danych
okolicznościach?
3) Czy istnieje lepszy algorytm od rozważanego? Czy jest on
optymalny?
Konstruując algorytm należy zwracać uwagę na :
- poprawność semantyczną
- prostotę
- czas działania
- ilość zajmowanej pamięci
- optymalność
- okoliczności w jakich należy go używać , a w jakich nie
Złożoność obliczeniową algorytmu definiuje się jako ilość zasobów
komputerowych, potrzebnych do jego wykonania.
Wyróżniamy złożoność pamięciową i czasową.
Będziemy się zajmować głównie złożonością czasową !!!
Miara złożoności musi być uniwersalna czyli oderwana od
szczegółów natury "sprzętowej" tj.
- Jaki komputer jest używany ?
- Jaka jest częstotliwość zegara taktującego procesor ?
- Czy program będzie jedynym wykonywanym na komputerze ?
Jeśli nie to jaki jest jego priorytet ?
- Jakiego kompilatora używamy?
- Czy w kompilatorze włączono opcje optymalizacji kodu ? ... etc
Parametrem najczęściej decydującym o czasie wykonania
algorytmu jest rozmiar danych, z którymi ma on do czynienia.
Parametr ten może mieć różne znaczenie:
- dla funkcji sortującej tablicę, czy funkcji wyszukiwania
linowego lub binarnego parametrem będzie rozmiar tablicy n
- dla dodawania, mnożenia macierzy, parametrem również
będzie rozmiar tablicy n
- dla funkcji liczącej n! będzie to wielkość danej wejściowej n
- dla ciągu Fibonacciego rozmiarem danych wejściowych może
być również liczba symboli użytych do zakodowania liczny n
(dla reprezentacji binarnej
⎣lg n ⎦ +1 )
- jeśli na wejściu algorytmu będzie graf to możemy podawać
liczbę wierzchołków i liczbę krawędzi jako rozmiar danych
wejściowych (2 liczby)
- dla niektórych zagadnien (problemow) mimo zastosowana tego
samego algorytmu możemy mieć inny rozmiar danych
W algorytmie zawsze można wyróżnić tzw.
operacje dominujące
lub
operacje podstawowe
(najbardziej czasochłonne) - takie, że
łączna ich liczba jest proporcjonalna do liczby wszystkich operacji
jednostkowych w dowolnej realizacji algorytmu.
Dla sortowania operacją tą będzie zwykle porównanie dwóch
elementów, lub także przestawienie elementów ciągu.
Nie jest jednoznacznie określone, które operacje należy traktować
jako dominujące, mogą to być porównania, ale również
dodawanie lub mnożenie.
Podstawowa analiza złożoności czasowej algorytmu określa, ile
razy operacja dominująca jest wykonywana dla kazdej wartości
rozmiaru danych wejściowych.
W niektórych przypadkach liczba
ta zależy nie tylko od rozmiaru danych wejściowych, ale również
od wartości wejściowych (np. przeszukiwanie linowe).
W innych przypadkach (np. dodawanie tablic), operacja
dominująca jest wykonywana zawsze tę samą liczbe razy dla
każdej realizacji problemu o rozmiarze n. W takich przypadkach
T(n)
definiujemy jako liczbę wykonań operacji dominującej przez
algorytm dla realizacji o rozmiarze danych n.
T(n)
jest wówczas nazywane
złożonością czasową w każdym
wypadku
.
W niektórych przypadkach dla pełnej analizy algorytmu należy
wybrac dwie różne operacje dominujące.
Jednostką złożoności czasowej jest czas wykonania jednej operacji
dominującej.
W ogólności wyróżniamy:
-
złożoność pesymistyczną
- zdefiniowaną jako ilość zasobów
komputerowych, potrzebnych przy "najgorszych" danych
wejściowych rozmiaru n
-
złożoność oczekiwaną
- definiowaną jako ilość zasobów
komputerowych, potrzebnych przy "typowych" danych
wejściowych rozmiaru n
W definicjach wykorzystujemy następujące wielkości:
D
n
- zbiór zestawów danych wejściowych rozmiaru n
t(d)
- liczba operacji dominujących dla zestawu danych
wejściowych d
X
n
- zmienna losowa równa t(d) dla d
∈ D
n
P
nk
- rozkład prawdopodobieństwa zmiennej losowej X
n
, tzn
prawdopodobieństwo, że dla danych rozmiaru n algorytm wykona
k operacji dominujących ( k
≥ 0 )
Zwykle przyjmujemy, że każdy zestaw danych rozmiaru n może
się pojawić z jednakowym prawdopodobieństwem.
Pesymistyczna złożoność czasowa to funkcja :
W(n)
= sup{ t(d) : d
∈ D
n
} czyli kres górny t(d)
Możliwe jest również określenie optymistycznej złożoności
czasowej
B(n)
= inf{ t(d) : d
∈ D
n
}, ale jest ona rzadko używana.
Oczekiwana złożoność czasowa (
złożoność w średnim przypadku
) to
funkcja:
A(n)
=
∑
k
≥ 0
( k*P
nk
) czyli wartość oczekiwana E( X
n
)
Oczywiście jeśli istnieje T(n) to W(n) = A(n) = T(n)
Aby stwierdzić, na ile W(n) i A(n) są reprezentatywne dla
wszystkich danych wejściowych wprowadza się dodatkowo:
- miarę
wrażliwości pesymistycznej
Δ(n)
= sup{ t(d
1
) - t(d
2
) : d
1
, d
2
∈ D
n
}
- miarę
wrażliwości oczekiwanej
( odchylenie standardowe )
________ _______________________
σ(n)
= dev( X
n
) =
√ var( X
n
) =
√ ∑
k
≥ 0
( k - E( X
n
) )
2
* P
nk
Im większe wartości
Δ(n) i σ(n) tym algorytm jest bardziej
wrażliwy na dane wejściowe i tym bardziej jego zachowanie może
odbiegać od tego opisanego funkcjami W(n) , A(n).
Przykład:
Przeszukiwanie liniowe zbioru (ciągu)
Problem: czy klucz x znajduje się w tablicy S, zawierajacej n
kluczy?
Dane wejściowe: całkowita liczba dodatnia n, tablica kluczy S
indeksowana od 1 do n oraz klucz x.
Wynik: location – lokalizacja klucza x w tablicy S (0, jeżeli x nie
występuje w S)
_________________________________________________
void linsearch(int n,
const keytype S[],
keytype x,
index& location)
{
location = 1;
while (location <= n && S[location] != x)
location++;
if(location > n)
location = 0;
}
________________________________________________
Rozmiar danych wejściowych: n
Operacja dominująca: S[location] != x
Pesymistyczna złożoność czasowa: W(n) = n+1
Pesymistyczna wrażliwość czasowa:
Δ(n) = n
Oczekiwana złożoność czasowa: A(n) = ?
Zakładamy, że P
nk
= 1/n dla k=1,2,3,...,n =>
A(n) =
∑
n
k = 1
(k* P
nk
) = 1/n *
∑ k = 1/n * n*(n+1)/2 = (n+1)/2
Oczekiwana wrażliwość czasowa ?
Var( X
n
) =
∑
n
k = 1
( k - (n+1)/2 )
2
*1/n =
= 1/n * ( n*(n+1)*(2n+2)/6 - 2(n+1)/2 *n*(n+1)/2 +n*( (n+1)/2 )
2
)
= (n+1)*(2n+1)/6 - (n+1)
2
/4 = (n+1)* (4n+2-3n-3)/12
= (n
2
- 1)/12
≈ n
2
/12
zatem
σ(n) ≈ 0.29*n
Ponieważ W(n), A(n) oraz
Δ
(n),
σ
(n) są liniowe w n , więc
algorytm ma dużą wrażliwość liczby operacji dominujących na
dane wejściowe.
Faktyczna/praktyczna złożoność czasowa algorytmu (czas
działania, T(n) ) zwykle różni się od wyliczonej teoretycznie
współczynnikiem proporcjonalności zależnym od konkretnej
realizacji algorytmu.
Istotną informacją zawarta w W(n), A(n) jest rząd wielkości , czyli
zachowanie asymptotyczne, gdy n ->
∞ .
Przykład (wyznaczanie złożoności praktycznej):
⎛ 0! = 1
N! =
⎢
⎝ n! = n* (n-1)! gdy n ≥ 1
______________________________________________
unsigned long int silnia(int x)
{
if (x==0)
return 1;
else
return x*silnia(x-1);
}
_______________________________________________
Przyjmujemy, że operacją dominującą jest instrukcja porównania
z czasem t
c
. Zatem:
T(0) = t
c
T(n) = t
c
+T(n-1) dla n
≥ 1
Należy uzyskać nie-rekurencyjną funkcję T(n)
T(n) = t
c
+ T(n-1)
T(n-1) = t
c
+ T(n-2)
T(n-2) = t
c
+ T(n-3)
...
...
...
T(1) = t
c
+ T(0)
T(0) = t
c
L = P =>
T(n) + T(n-1) + ... + T(0) = (n+1)* t
c
+ T(n-1) + ...+ T(0)
=> T(n) = (n+1)* t
c
W praktyce nieistotna jest taka dokładność dla złożoności
praktycznej T(n) i różnice między np. T(n) = (n+1)* t
c
i np.
T(n) = (n+3)* t
c
można zaniedbać.
Będziemy zatem szukać złożoności teoretycznej, tj. funkcji
matematycznej występującej w T(n), która odgrywa w niej
najważniejszą rolę, wpływając najsilniej na czas wykonania
programu.
Złożoność teoretyczną
, inaczej
klasę algorytmu
O( T(n) )
definiujemy:
O(T(n)) =
{g:T:N->
ℜ
+
(
∃ M ∈ ℜ
+
)(
∃ n
0
∈ N )( ∀ n ≥ n
0
) [
⏐g(n)⏐≤⏐M*T(n)⏐ ] }
( klasą O dowolnej funkcji T:N->
ℜ
+
jest taka funkcja g , że
istnieje M oraz n
0
takie, że dla każdego n
≥ n
0
zachodzi
⏐g(n)⏐≤⏐M*T(n)⏐ )
np.
T(n) = 3n+1 => O(T(n)) = O(n)
T(n) = n
2
-n+1 => O(T(n)) = O( n
2
)
T(n) = 2
n
+n
2
+4 => O(T(n)) = O( 2
n
)
Klasa O (będąca zbiorem funkcji ) jest wielkością asymptotyczną,
pozwalającą wyrazić w postaci arytmetycznej wielkości z góry nie
znane w postaci analitycznej.
Własności funkcji O :
c*O( f(n) ) = O( f(n) )
O( f(n) ) + O( f(n) ) = O( f(n) )
O(O( f(n) ) ) = O( f(n) )
O( f(n) ) * O( g(n) ) = O( f(n)*g(n) )
O( f(n) * g(n) ) = f(n)*O( g(n) )
Najczęściej spotykane złożoności czasowe algorytmów:
1)
log(n)
- występuje, np. dla algorytmów, w których zadanie
rozmiaru n zostaje sprowadzone do zadania rozmiaru n/2 +
pewna stała liczba działań ( np. przeszukiwanie binarne
uporządkowanego ciągu)
2)
n
- występuje, np. dla algorytmów, w których jest wykonywana
pewna stała liczba działań dla każdego z n elementów danych
wejściowych (np. algorytm Hornera wyznaczania wartości
wielomianu)
3)
n*log(n)
- występuje, np. dla algorytmów, w których zadanie
rozmiaru n zostaje sprowadzone do dwóch podzadań rozmiaru
n/2 + pewna liczba działań liniowa w n (np. niektóre metody
sortowania - quicksort )
4)
n
2
- występuje, np. dla algorytmów w których jest wykonywana
pewna stała liczba działań dla każdej pary elementów danych
wejściowych (podwójna instrukcja iteracyjna, np. operacje na
tablicach)
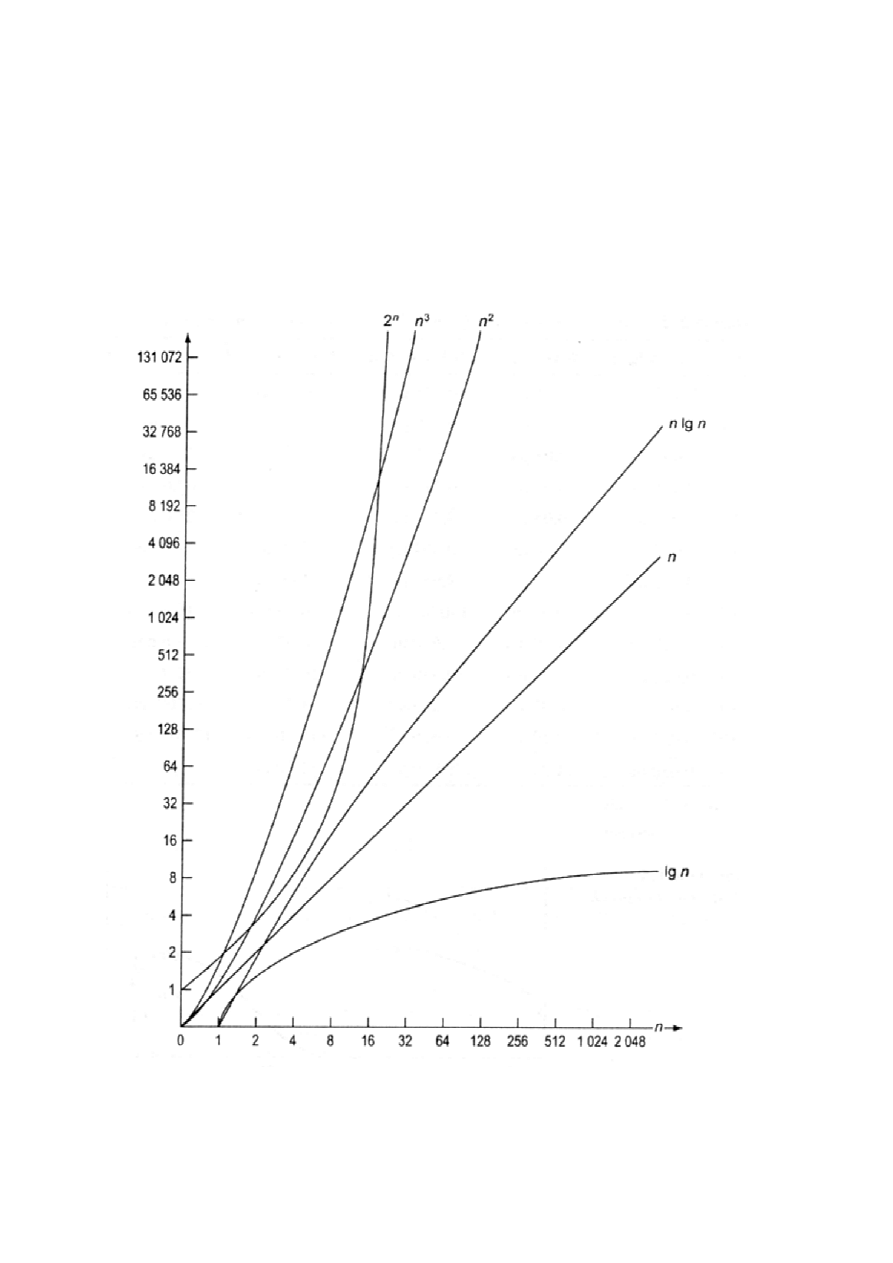
5)
2
n
- występuje, np. dla algorytmów, w których jest wykonywana
stała liczba działań dla każdego podzbioru danych wejściowych
6)
n!
- występuje, np. dla algorytmów, w których jest
wykonywana stała liczba działań dla każdej permutacji danych
wejściowych
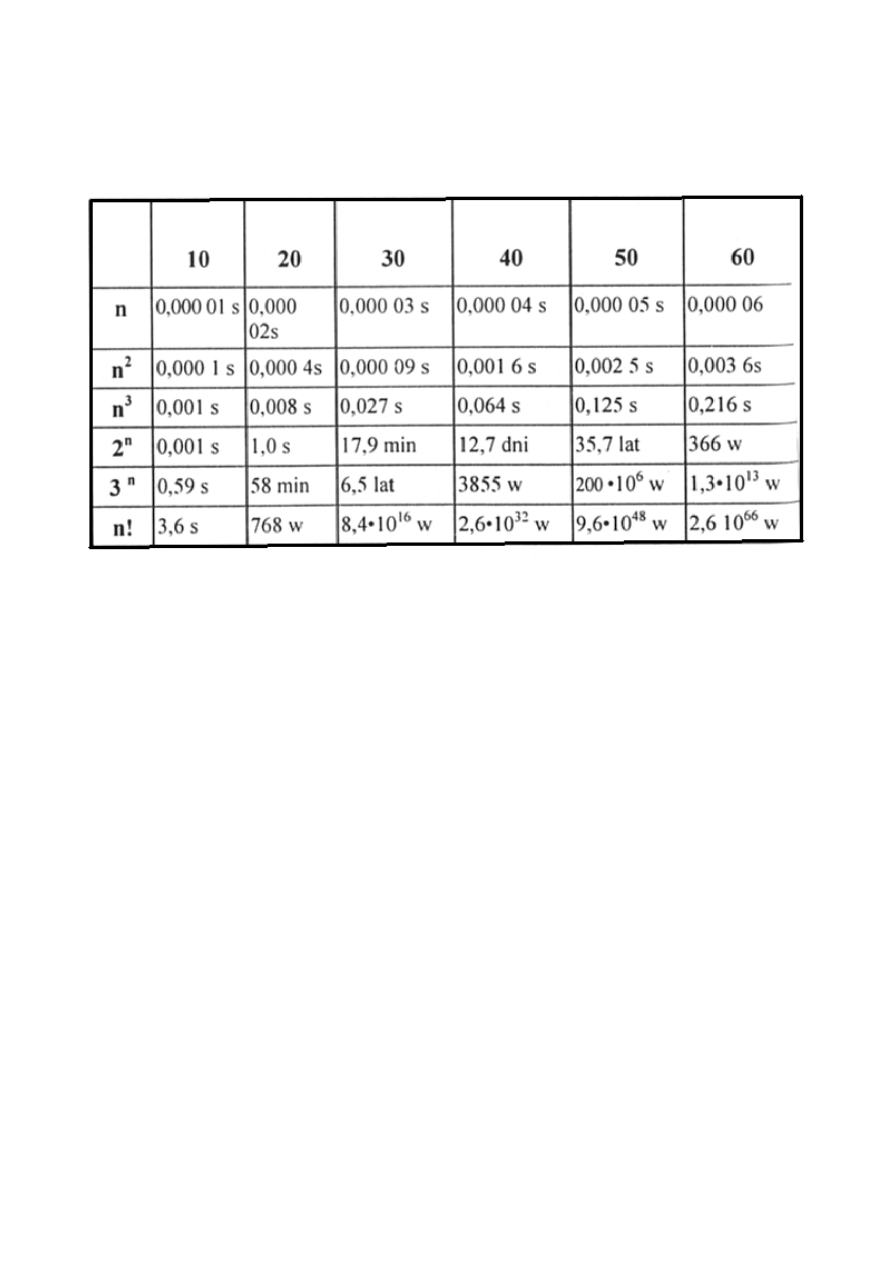
Czas działania algorytmu/ programu o danym rozmiarze danych
n silnie zależy od złożoności algorytmu:
Tc = 1
μs
Należy zawsze pamiętać o asymptotycznym charakterze klasy
algorytmu O.
Przykład:
Mamy dwa algorytmy:
W1 klasy O(logN) (złożoność praktyczna 100*log
2
N)
W2 klasy O(N) (złożoność praktyczna 10*N)
Dla N=2 , dla W1, T(N)=100 > dla W2, T(N)=20
Dla N=1024, dla W1, T(N)=1000 < dla W2, T(N)=10240
Zatem dla wystarczająco dużego N algorytm W1 jest bardziej
efektywny niż W2.
Jeszcze jeden przykład wyznaczania złożoności czasowej algorytmu
(zerowanie tablicy poniżej przekątnej wraz z nią):
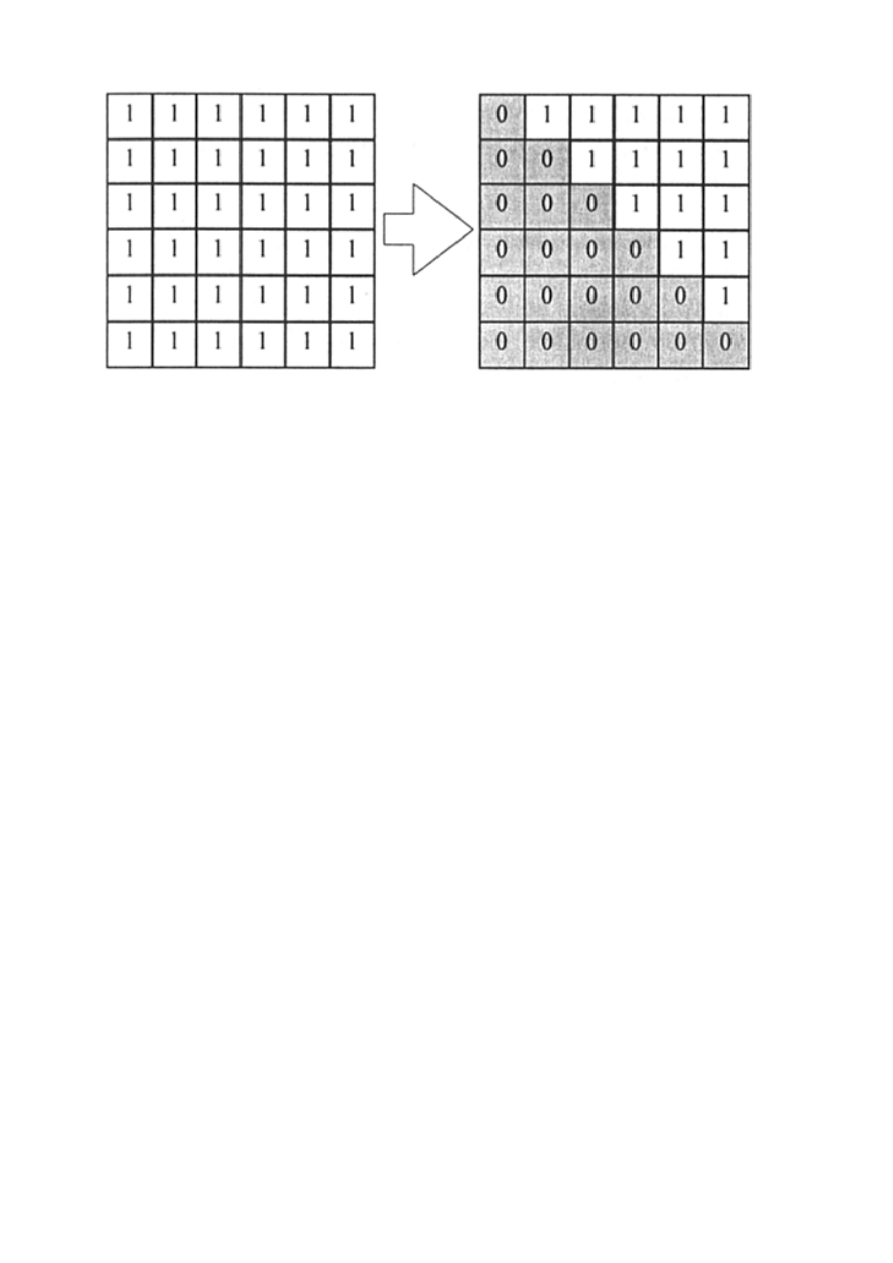
int tab[n][n];
void zerowanie( )
{
int i,j;
i=0; // ta
while (i< n) // tc
{
j=0; // ta
while (j<=i) // tc
⎞
{
⎢
∑
j
(tc+2ta)
tab[i,j]=0; // ta
⎢
j=j+1; // ta
⎠
}
i=i+1; // ta
}
}
gdzie ta - czas wykonania instrukcji przypisania
tc - czas wykonania instrukcji porównania
Pamiętając, że instrukcja while powtarza n razy instrukcje zawarte
pomiędzy nawiasami, a warunek jest sprawdzany n+1 razy można
zapisać:
T(N) = tc + ta +
∑
N
i=1
( 2*ta + 2*tc +
∑
i
j=1
(tc + 2*ta) )
i po usunięciu wewnętrznej sumy dostajemy:
T(N) = tc + ta +
∑
N
i=1
( 2*ta + 2*tc + i*(tc + 2*ta) ) =
tc + ta +
2*N*(ta + tc) + N*(N+1)*(tc+2*ta)/2 )
i po uproszczeniu
T(N) = ta (1+3*N+
N
2
) + tc*(1+2.5*tc+
N
2
/2 )
⇒ program jest klasy O(n
2
)
Powyższe przykłady miały jedną wspólną cechę: czas wykonania
programu nie zależał od wartości danych, a jedynie od ich rozmiarów.
Przykład (fragment programu)
const n=10;
int t[n];
void sumowanie( )
{
int i,k;
int suma=0;
i=0; // ta = 0
while (i<n) // tc = 1
{
j=0; // ta = 0
while (j<=t[i]) // tc = 1
{
suma=suma+2; // ta = 0
j=j+1; // ta = 0
}
i=i+1; // ta = 0
}
}
Problemem jest fakt, że nie znamy zawartości tablicy t[N].
T(n) = tc +
∑
N
i=1
( tc +
∑
t[i]
j=1
( tc ) )
T(n) = tc + N*tc +
∑
N
i=1
(t[i]*tc )
T(n) = tc + N*tc + N*t[i]*tc
T(n) = tc*( 1 + N + N*t[i] )
T(n)
≈ max( N , N*t[i] )
Możemy zatem jedynie powiedzieć, że czas wykonania jest
proporcjonalny do większej z liczb N i N*t[i], ale nie jesteśmy w
stanie określić dokładnej wartości.
Problemem jest nieznajomość zawartości tablicy, która jest potrzebna
do otrzymania ostatecznego wyniku. Jedyne co można zrobić to
przeprowadzić analizę statystyczną zadania.
Niekiedy możemy znacząco uprościć obliczenia zakładając:
- zwracamy uwagę tylko na najbardziej „czasochłonne” operacje
(najczęściej instrukcje porównania).
- wybieramy wiersz programu znajdujący się w najgłębiej położonej
instrukcji iteracyjnej (pętle w pętlach ...) i obliczamy ile razy jest
on wykonywany. Z wyniku dedukujemy złożoność teoretyczną.
i=0;
while (i<N)
{
j=0;
while (j<=N)
{
suma=suma+2;
j=j+1;
}
i=i+1;
}
Wybierając instrukcję suma:=suma+2 obliczamy w prosty
sposób, że wykona się ona N(N+1) razy. Zatem fragment
programu ma złożoność teoretyczną O(n
2
).
Analiza równań rekurencyjnych
W rozwiązaniach równań rekurencyjnych stosuje się zwykle dwie
metody:
- rozwinięcie równania do sumy
- znalezienia funkcji tworzącej
Rozwinięcie do sumy
Przykłady wyznaczania praktycznej złożoności czasowej T(n) :
1)
⎧ T(1) = 0
⎨
⎩ T(n) = T( ⎣ n/2 ⎦ ) + c dla n > 1
Zależność tą otrzymujemy jako równanie złożoności, gdy problem
rozmiaru n sprowadza się do pod-problemu rozmiaru o połowę
mniejszego.
Podstawiamy n=2
k
.
T(n) = T( 2
k
) = T( 2
k-1
) + c = T( 2
k-2
) + c + c = T( 2
0
) + k*c = k*c
= c*logn
O(T(n)) = logn
2)
⎧ T(1) = 0
⎨
⎩ T(n) = T( ⎣ n/2 ⎦ ) + T( ⎡ n/2 ⎤ ) + c dla n > 1
Zależność tą otrzymujemy jako równanie złożoności, gdy problem
rozmiaru n sprowadza się do dwóch pod-problemów rozmiaru n/2
+ stała liczba działań.
Podstawiamy n=2
k
.
T(n) = T( 2
k
) = 2*T( 2
k - 1
) + c = 2*( 2*T( 2
k - 2
) + c ) + c =
2
2
*T( 2
k - 2
)+2
1
*c + 2
0
*c = 2
k
*T(2
0
) + c*( 2
k - 1
+ 2
k - 2
+...+ 2
0
)
= 0 + c*(2
k
- 1) / (2 - 1) = c * (n-1)
O(T(n)) = n
3)
⎧ T(1) = 0
⎨
⎩ T(n) = T( ⎣ n/2 ⎦ ) + T( ⎡ n/2 ⎤ ) + c*n dla n > 1
Zależność tą otrzymujemy jako równanie złożoności, gdy problem
rozmiaru n sprowadza się do dwóch pod-problemów rozmiaru n/2
+ liniowa liczba działań.
Podstawiamy n=2
k
.
T(n) =T(2
k
) = 2*T( 2
k - 1
) + c* 2
k
= 2*( 2*T( 2
k - 2
) + c*2
k - 1
) + c*2
k
= 2
2
*T( 2
k - 2
) + c*2
k
+ c*2
k
= 2
k
*T(2
0
) + k*c* 2
k
=
= 0 + c*n*logn = c*n*logn
O(T(n)) = n*logn
Zmiana dziedziny równania rekurencyjnego
Niektóre równania charakteryzują się nieprzyjemnym wyglądem i
nie dają się rozwiązać wcześniejszymi wzorami.
Czasem skutkuje zmiana dziedziny.
Przykładowo:
a
n
= (3*a
n-1
)
2
a
0
= 1
Podstawiamy b
n
= log
2
a
n
, b
n-1
= log
2
a
n-1
i logarytmujemy obie
strony równania
b
n
= log
2
a
n
= log
2
(3*a
n-1
)
2
b
0
= log
2
1 = 0
Dostajemy wersję b
n
= 2* log
2
3 + 2*b
n-1
która nadaje się już do
rozwiązania.
Funkcje tworzące
Czasem trudno wyznaczyć rozwiązanie T(n) bezpośrednio z
równania rekurencyjnego (brak zwięzłego wzoru).
Poszukujemy wówczas funkcji tworzącej, definiowanej jako:
F(z) =
∑
n
≥ 0
T(n)* z
n
Metodę tę stosuje się do znajdowania wartości oczekiwanej i
wariancji zmiennej losowej X
n
.
Funkcja tworząca dla rozkładu prawdopodobieństwa P
nk
zmiennej losowej X
n
ma postać:
P
n
(z) =
∑
k
≥ 0
P
nk
* z
k
i wtedy
∑
k
≥ 0
P
nk
= 1
Wartość oczekiwaną i wariancję można wyznaczyć jako funkcję
pochodnych funkcji P
n
(z) dla z = 1 :
E( X
n
) = P
′
n
(1) (*)
var( X
n
) = P
″
n
(1) + P
′
n
(1) - P
′
n
(1)
2
(**)
Ponieważ:
P
′
n
(z) =
∑
k
≥ 1
k*P
nk
* z
k - 1
P
″
n
(z) =
∑
k
≥ 2
k*(k-1)*P
nk
* z
k - 2
Stąd:
P
′
n
(1) =
∑
k
≥ 1
k*P
nk
⇒ (*)
P
″
n
(1) =
∑
k
≥ 2
k*(k-1)*P
nk
Zatem:
Var( X
n
) =
∑
k
≥ 0
( k - P
′
n
(1) )
2
* P
nk
=
∑
k
≥ 0
k
2
* P
nk
- 2*P
′
n
(1)*(
∑
k
≥ 0
k*P
nk
) + P
′
n
(1)
2
*(
∑
k
≥ 0
P
nk
)
=
∑
k
≥ 0
k*(k-1)*P
nk
+
∑
k
≥ 0
k*P
nk
- 2*P
′
n
(1)
2
+ P
′
n
(1)
2
= P
″
n
(1) + P
′
n
(1) - P
′
n
(1)
2
Wielkości E( X
n
) i var( X
n
) , a także złożoność oczekiwaną i
wrażliwość algorytmu, można wyznaczyć nie znając rozkładu P
nk
,
a tylko funkcję tworzącą.
Funkcja Ackermanna
Przykład pokazuje jak niegroźna „z wyglądu” funkcja
rekurencyjna może być bardzo kosztowna w użyciu.
int A(int n, int p)
{
if (n==0)
return 1;
if ((p==0) && (n>=1))
if (n==1)
return 2;
else return n+2;
if ((p>=1) && (n>=1))
return A( A(n-1 ,p), p-1 );
}
Dlaczego pojawia się komunikat „Stack, overflow” (przepełnienie
stosu) ?
Komunikat sugeruje, że podczas wykonania programu nastąpiła
znaczna ilość wywołań funkcji Ackermanna.
Z analizy funkcji A uzyskujemy:
∀ n ≥ 1 , A(n,1) = A(A(n-1,1),0) = A(n-1,1) + 2
co daje
∀ n ≥ 1 , A(n,1) = 2n
Analogicznie dla 2 otrzymamy:
∀ n ≥ 1 , A(n,2) = A(A(n-1,2),1) = 2A(n-1,2)
co pozwala napisać
∀ n ≥ 1 , A(n,2) = 2
n
W przypadku funkcji Ackermanna trudno jest nawet nazwać
jej klasę. Stwierdzenie, że zachowuje się wykładniczo jest
zdecydowanie niepoprawne.