Krzysztof Pancerz

Algorytmy i struktury danych

Algorytmy

i

struktury danych

WYKŁAD 1

Dr inż. Krzysztof Pancerz

Krzysztof Pancerz

Algorytmy i struktury danych

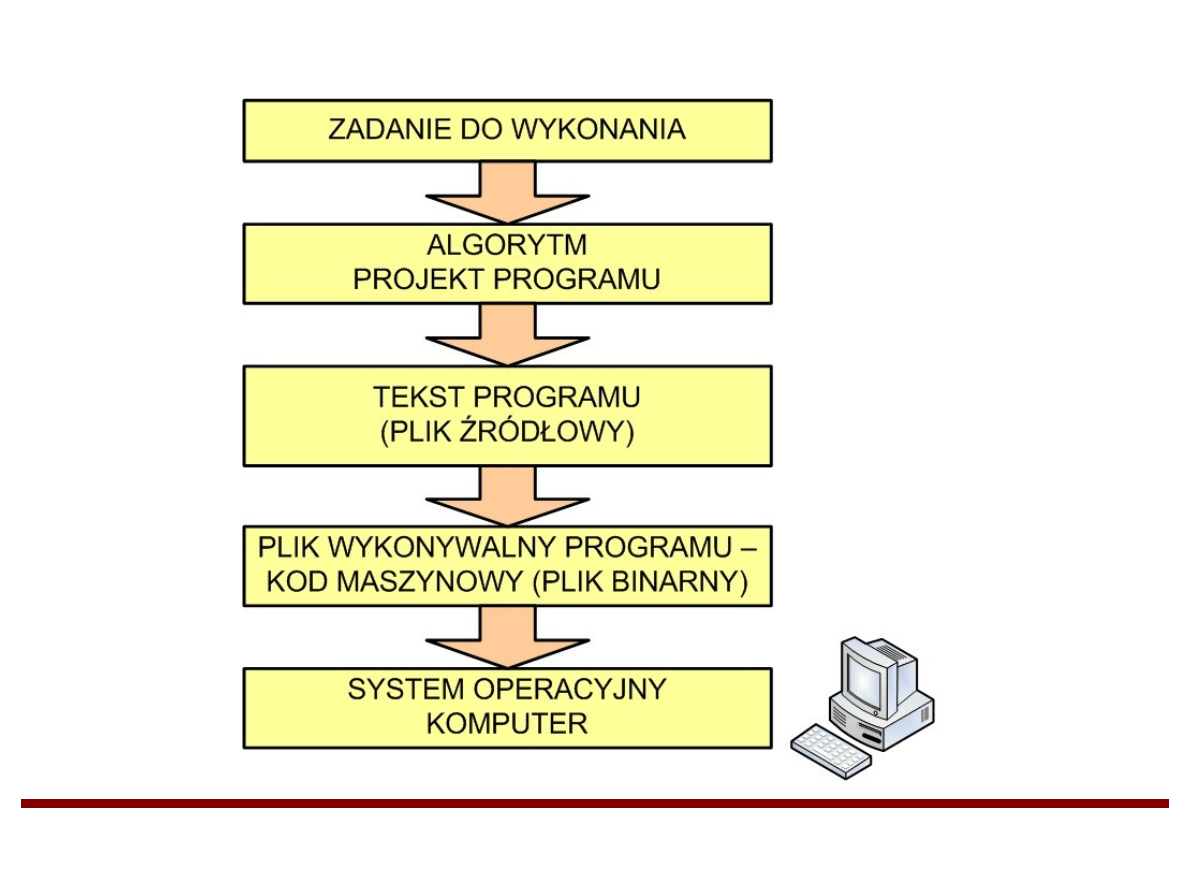
Proces tworzenia i uruchamiania programów

Krzysztof Pancerz

Algorytmy i struktury danych

Algorytm, program

●

Algorytm – przepis postępowania prowadzący
do rozwiązania określonego zadania.

●

Program – zapis algorytmu i danych w
konkretnym języku programowania.

●

Generalnie, program realizuje przetwarzanie
określonych danych wejściowych (podawanych
przez użytkownika) w dane wyjściowe (wynik
działania programu).

Krzysztof Pancerz

Algorytmy i struktury danych

Algorytm, program (cd.)

Algorytmy + Struktury danych

=

Programy

(

tytuł książki Niklausa Wirtha

)

Krzysztof Pancerz

Algorytmy i struktury danych

Sposoby reprezentacji algorytmów

●

Język naturalny.

●

Lista kroków.

●

Drzewo algorytmu.

●

Schemat blokowy.

●

Pseudokod (mniej formalny, bardziej intuicyjny
system notacji).

●

Kod w języku programowania.

Krzysztof Pancerz

Algorytmy i struktury danych

Własności algorytmów

●

Skończoność (realizowany ciąg operacji
powinien mieć swój koniec).

●

Określoność (operacje oraz porządek ich
wykonywania powinny być ściśle określone).

●

Ogólność (algorytm powinien odnosić się nie
tylko do jednego szczególnego przypadku, ale
do pewnej klasy zadań).

●

Efektywność (algorytm powinien prowadzić do
rozwiązania możliwie najprostszą drogą).

Krzysztof Pancerz

Algorytmy i struktury danych

Całkowita poprawność algorytmu

●

Algorytm jest całkowicie poprawny jeśli dla
każdych danych wejściowych spełniających
wymagane warunki wstępne zatrzymuje się i
daje poprawny wynik.

●

Dowód poprawności algorytmu:

–

udowodnienie własności stopu (dla każdych danych

wejściowych spełniających wymagane warunki

wstępne algorytm zatrzymuje się),

–

udowodnienie częściowej poprawności (jeśli

algorytm zatrzymuje się to daje poprawny wynik).

Krzysztof Pancerz

Algorytmy i struktury danych

Całkowita poprawność algorytmu (cd.)

Całkowita poprawność

=

Własność stopu

+

Częściowa poprawność

Krzysztof Pancerz

Algorytmy i struktury danych

Podstawowe typy danych w języku C/C++

●

Typ danej określa zbiór jej możliwych wartości
oraz zestaw operacji, które można nad nimi
wykonywać. Jednocześnie określa on rozmiar
pamięci potrzebny do przechowywania danej
oraz sposób zapisu danej.

Krzysztof Pancerz

Algorytmy i struktury danych

Podstawowe typy danych w języku C/C++ (cd.)

●

short, int, long – typy reprezentujące liczby
całkowite,

●

usigned short, unsigned int, unsigned long
– typy reprezentujące liczby całkowite,

●

float, double – typy reprezentujące liczby
rzeczywiste,

●

char – typ reprezentujący znaki.

Krzysztof Pancerz

Algorytmy i struktury danych

Literały

●

Literały całkowite

–

np. 12, -34

●

Literały rzeczywiste

–

np. 1.2, -3.45, 0.1E2, 1.0E-10

●

Literały znakowe

–

np. 'a', '&'

Krzysztof Pancerz

Algorytmy i struktury danych

Zmienne

●

Zmienna jest identyfikatorem, który podczas
działania programu może przyjmować różne
wartości ze zbioru określonego za pomocą
typu. Każda zmienna używana w programie
musi zostać zadeklarowana.

Deklaracja zmiennej:
typ nazwa;
Przykład deklaracji:
int a;

Krzysztof Pancerz

Algorytmy i struktury danych

Operator przypisania

Operator przypisania = służy do ustalenia

wartości zmiennej.

Przykład
x=y oznacza, że wartość y przypisywana jest do

zmiennej x.

Krzysztof Pancerz

Algorytmy i struktury danych

Operatory arytmetyczne

+

dodawanie

-

odejmowanie

*

mnożenie

/

dzielenie

%

reszta z dzielenia

-

zmiana znaku liczby

Krzysztof Pancerz

Algorytmy i struktury danych

Operatory arytmetyczne (cd.)

++

inkrementacja (zwiększanie o 1)

- -

dekrementacja (zmniejszanie o 1)

Krzysztof Pancerz

Algorytmy i struktury danych

Operatory logiczne

&&

iloczyn logiczny (koniunkcja)

||

suma logiczna (alternatywa)

!

negacja

a

b

a && b

a || b

!a

false

flase

false

false

true

false

true

false

true

true

true

false

false

true

false

true

true

true

true

false

Krzysztof Pancerz

Algorytmy i struktury danych

Operatory relacyjne

==

równy

!=

różny

<

mniejszy

<=

mniejszy lub równy

>

większy

>=

większy lub równy

Krzysztof Pancerz

Algorytmy i struktury danych

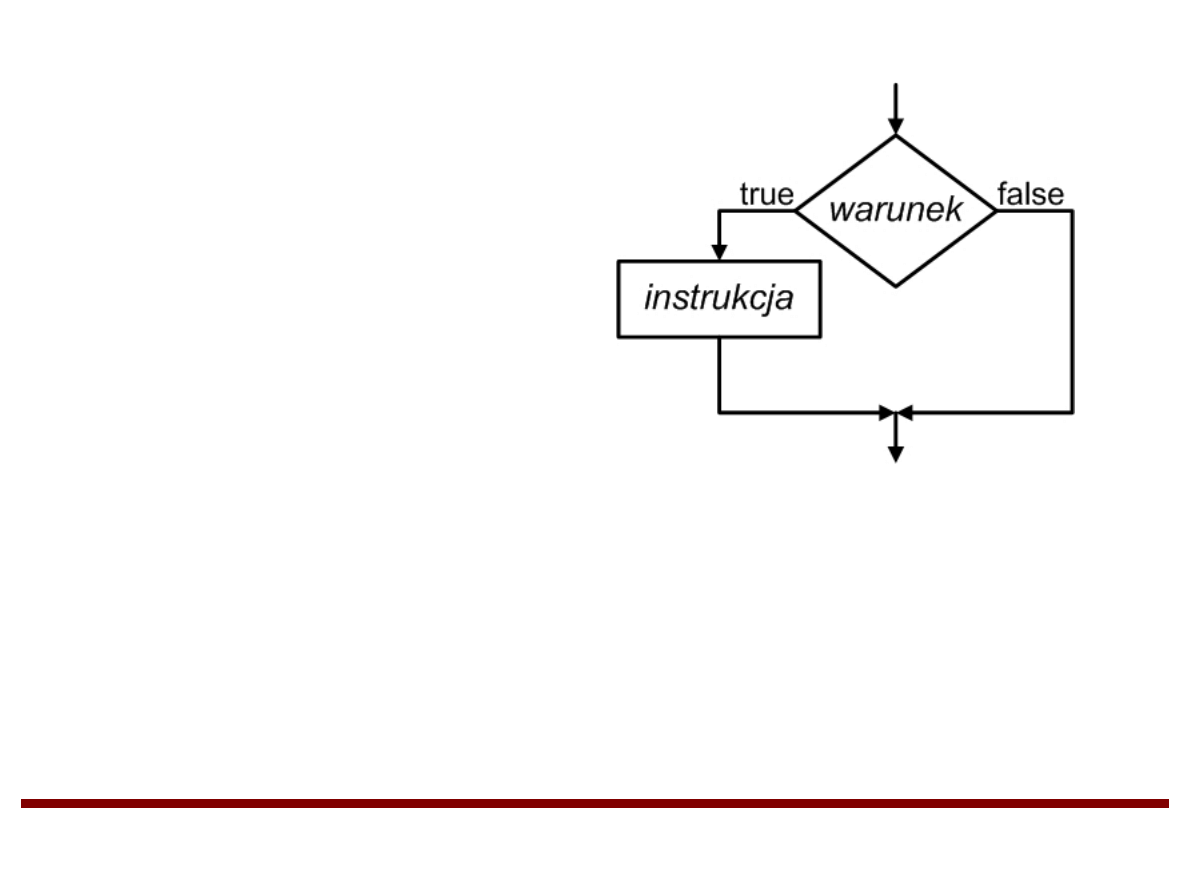
Instrukcja warunkowa IF

if (warunek)
instrukcja

●

Jeśli warunek jest prawdziwy (true), instrukcja zostaje

wykonana i sterowanie przenoszone jest do kolejnych instrukcji

po instrukcji warunkowej.

●

Jeśli warunek nie jest prawdziwy (false), instrukcja nie zostaje

wykonana, a sterowanie przenoszone jest bezpośrednio do
kolejnych instrukcji po instrukcji warunkowej.

●

instrukcja może być instrukcją złożoną { }.

Krzysztof Pancerz

Algorytmy i struktury danych

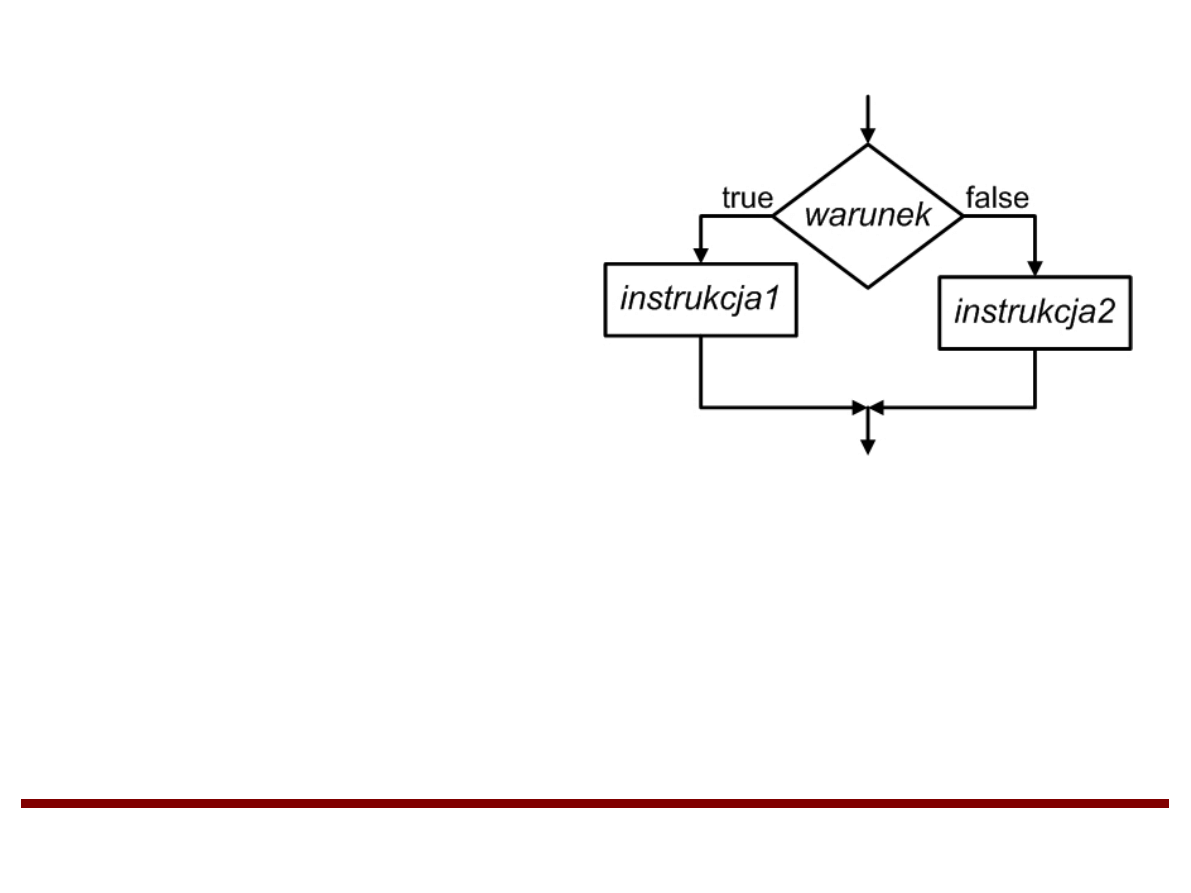
Instrukcja warunkowa IF-ELSE

if (warunek)
instrukcja1
else
instrukcja2

●

Jeśli warunek jest prawdziwy (true), tylko instrukcja1 zostaje

wykonana i sterowanie przenoszone jest do kolejnych instrukcji

po instrukcji warunkowej.

●

Jeśli warunek nie jest prawdziwy (false), tylko instrukcja2 zostaje

wykonana i sterowanie przenoszone jest do kolejnych instrukcji
po instrukcji warunkowej.

●

instrukcja1 oraz instrukcja2 mogą być instrukcjami złożonymi { }.

Krzysztof Pancerz

Algorytmy i struktury danych

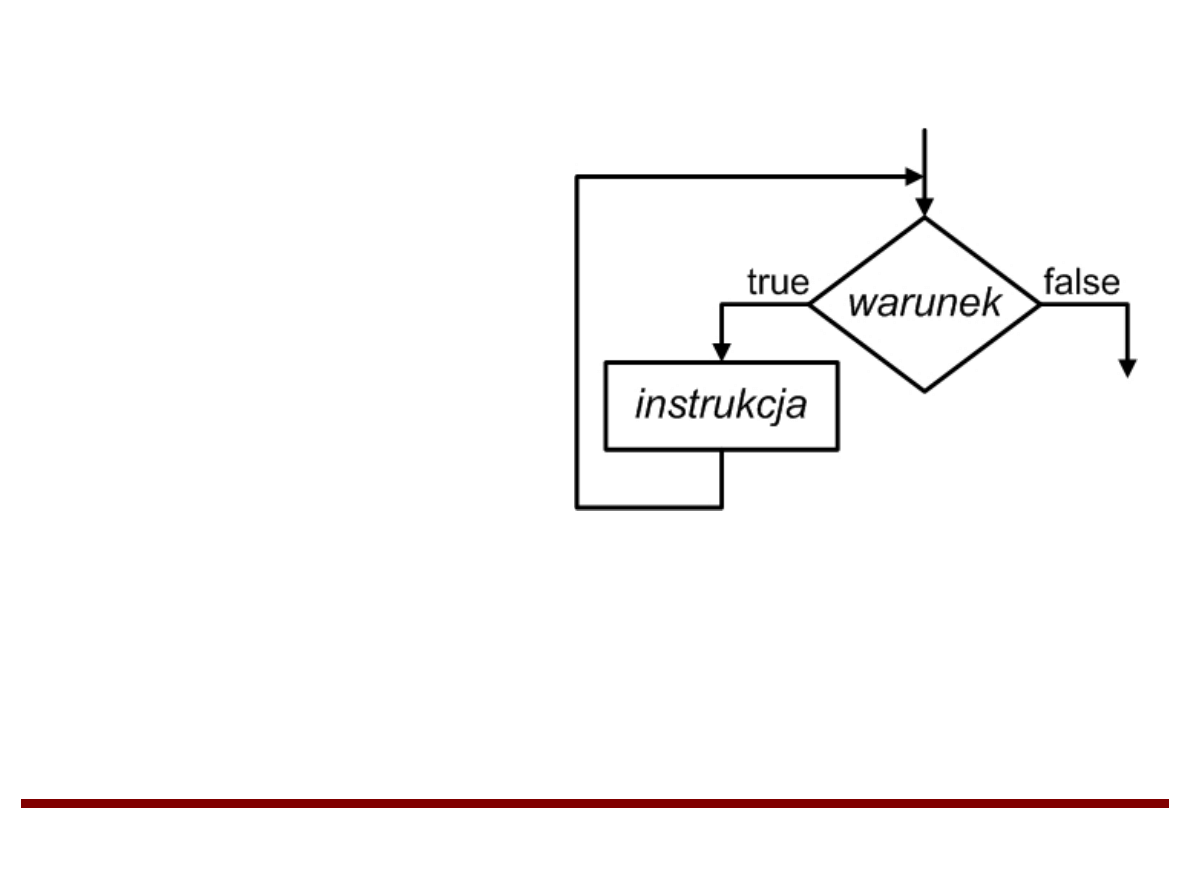
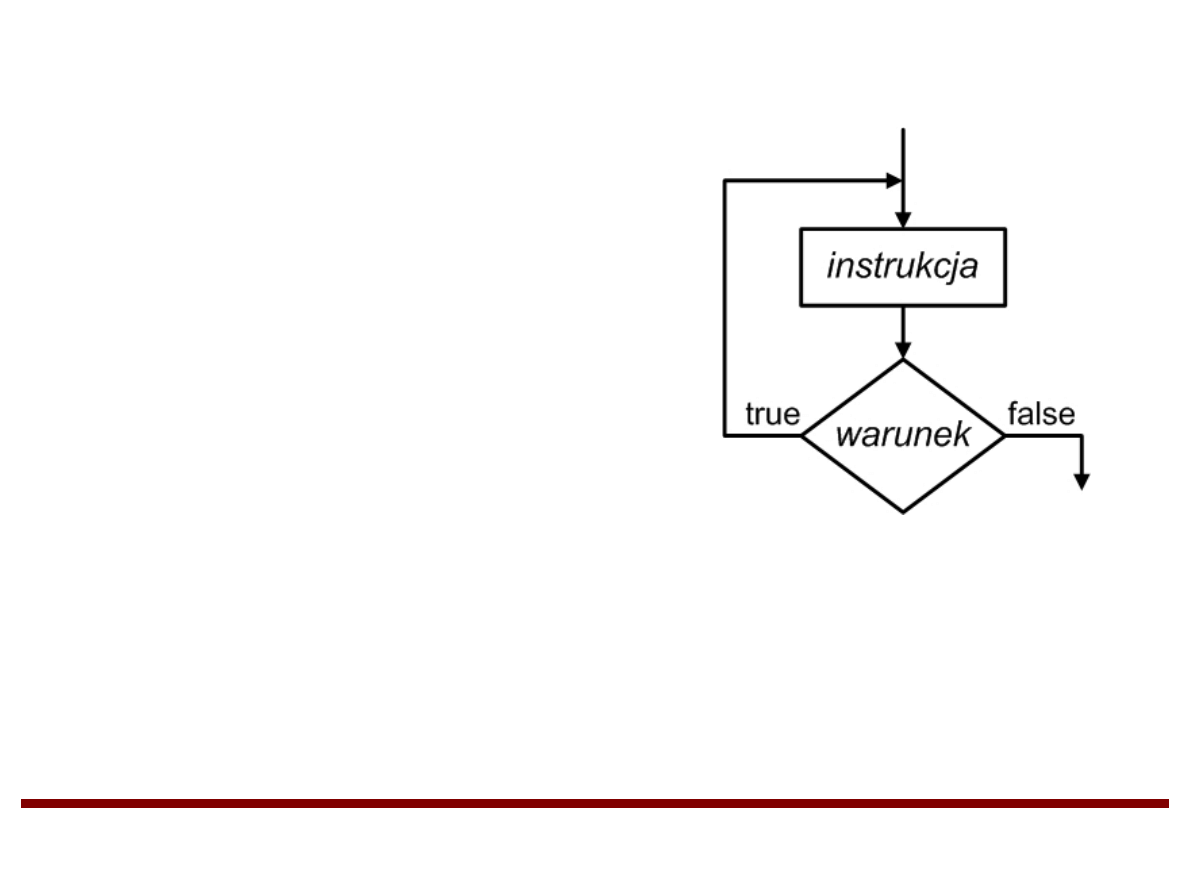
Instrukcja iteracyjna (pętla) WHILE

while (warunek)
instrukcja

●

Dopóki warunek jest prawdziwy (true), instrukcja jest

wykonywana. Gdy warunek przestaje być prawdziwy (false)

sterowanie przenoszone jest do kolejnych instrukcji po
instrukcji WHILE.

●

instrukcja może być instrukcją złożoną { }.

Krzysztof Pancerz

Algorytmy i struktury danych

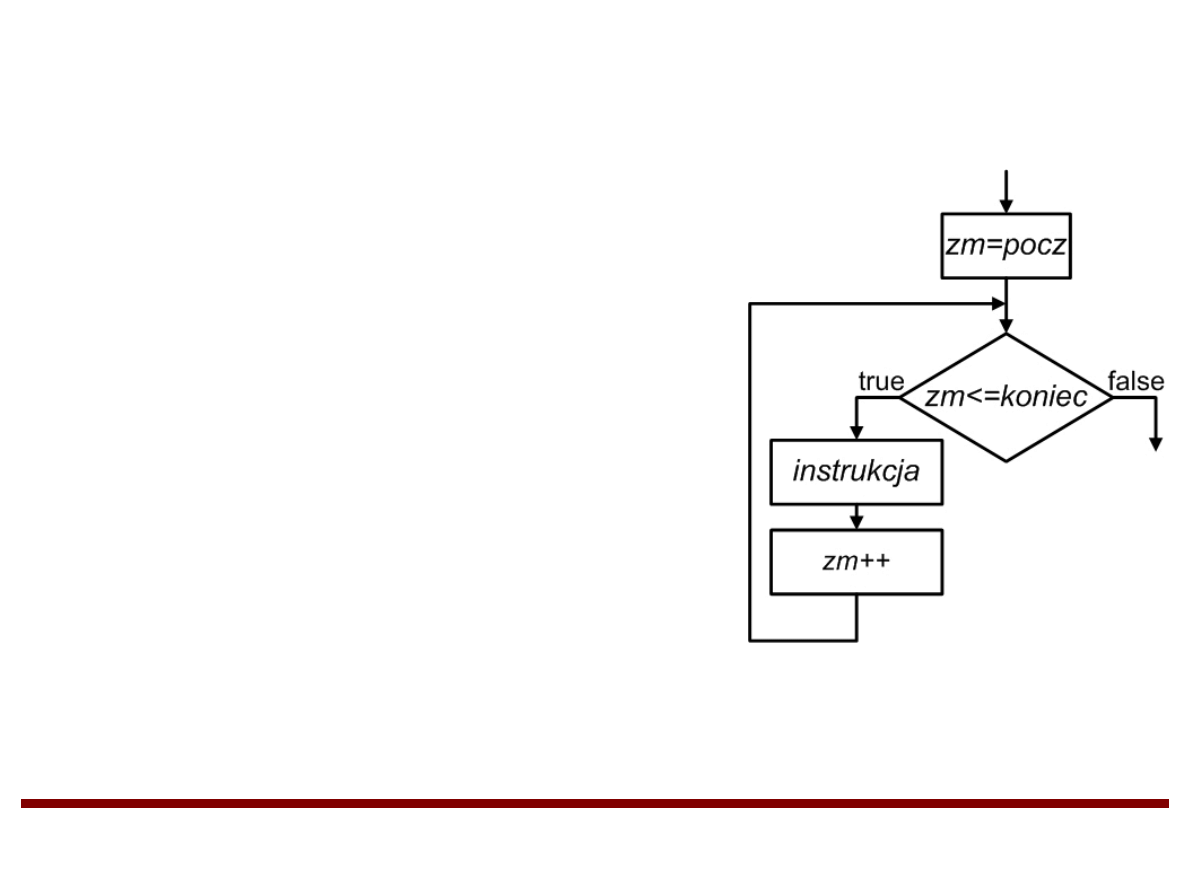
Instrukcja iteracyjna (pętla) DO-WHILE

do {
instrukcja
}
while (warunek);

●

Pętla DO-WHILE działa podobnie jak pętla WHILE. Różnica

polega na tym, że warunek jest testowany po wykonaniu

instrukcji. W związku z tym instrukcja zostaje wykonana co
najmniej jeden raz.

Krzysztof Pancerz

Algorytmy i struktury danych

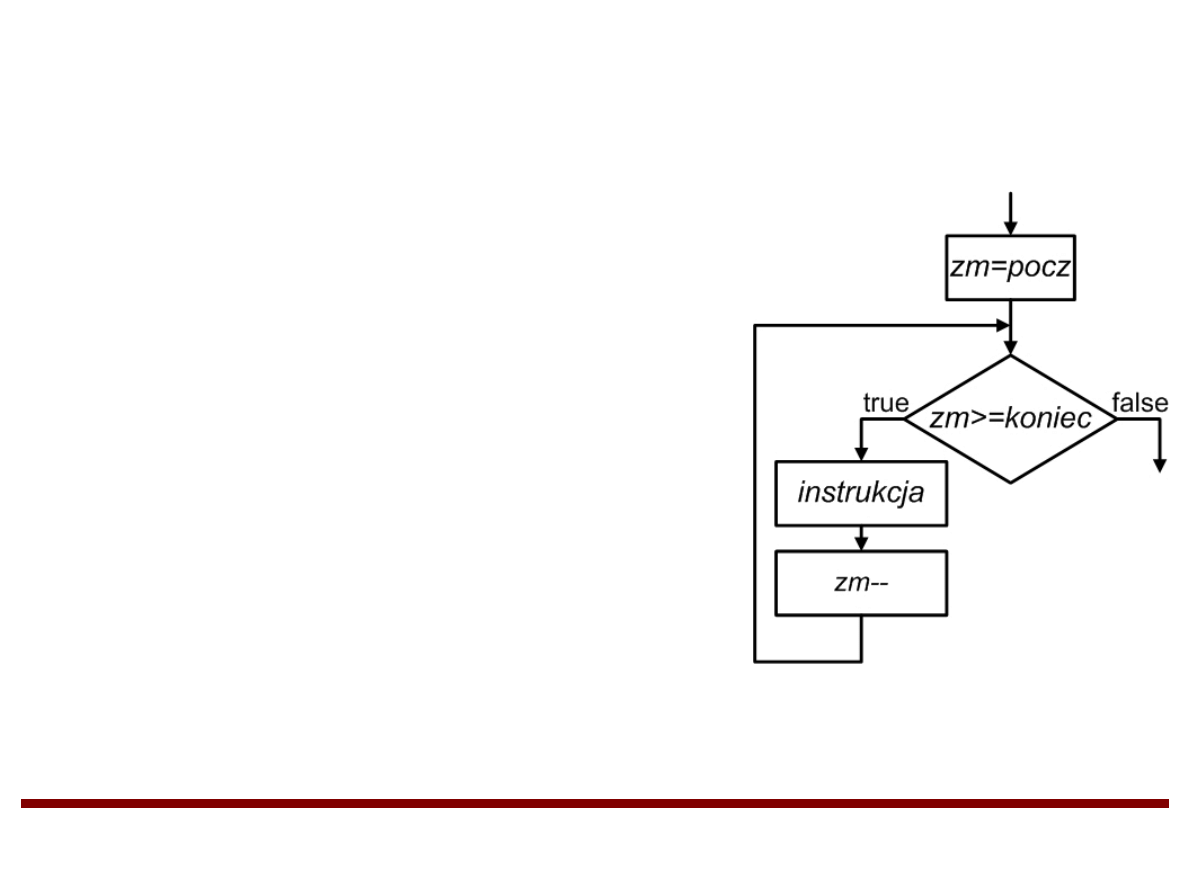
Instrukcja iteracyjna (pętla) FOR

for (zm=pocz; zm<=koniec; zm++)
instrukcja

●

pocz oraz koniec są wyrażeniami typu

całkowitego.

●

Zmiennej zm przypisywana jest

wartość pocz. Dopóki wartość zmiennej

jest mniejsza lub równa wartości koniec,
instrukcja jest wykonywana. Za każdym

razem wartość zmiennej zwiększana
jest o 1. Gdy wartość zmiennej zm staje

się większa od wartości koniec
sterowanie jest przenoszone do
kolejnych instrukcji po instrukcji FOR.

●

instrukcja może być instrukcją złożoną

{ }.

Krzysztof Pancerz

Algorytmy i struktury danych

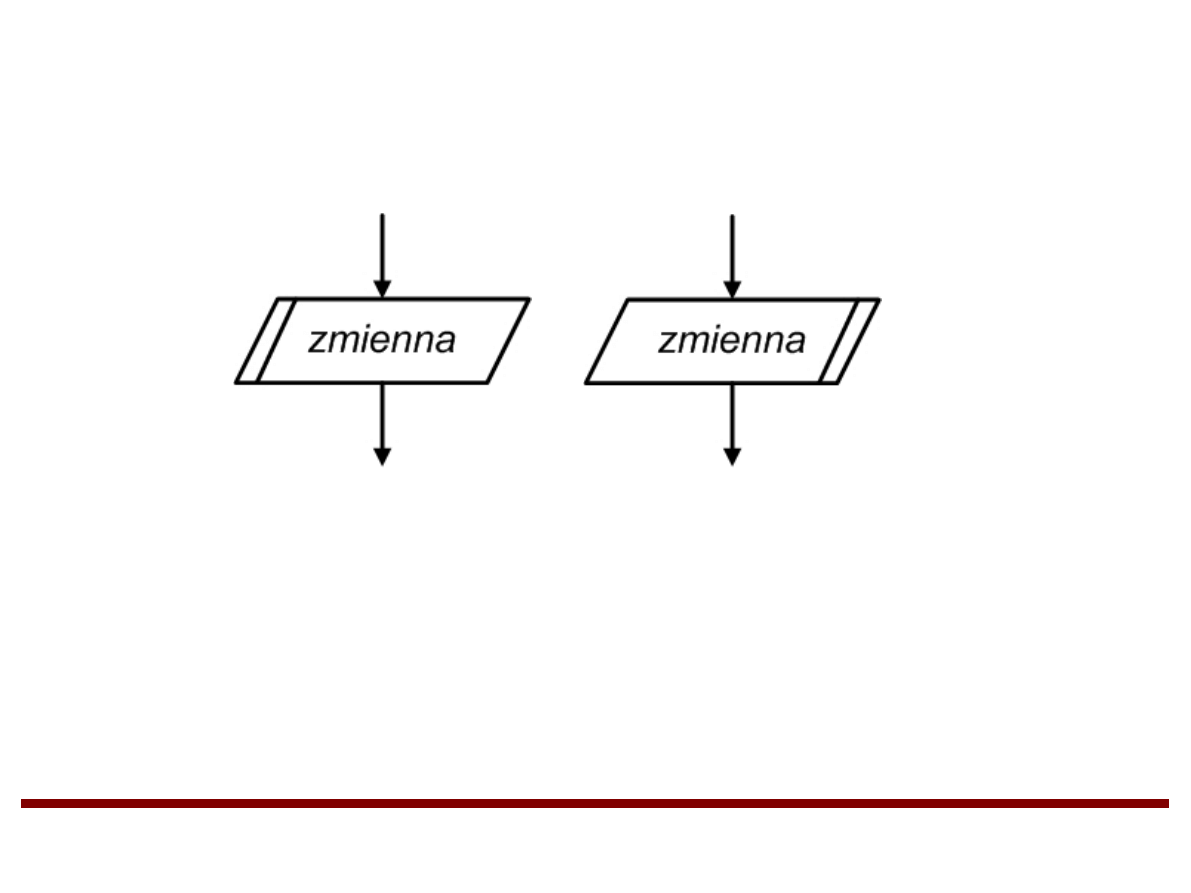
Instrukcja iteracyjna (pętla) FOR (cd.)

for (zm=pocz; zm>=koniec; zm--)
instrukcja

●

pocz oraz koniec są wyrażeniami typu

całkowitego.

●

Zmiennej zm przypisywana jest

wartość pocz. Dopóki wartość zmiennej

jest większa lub równa wartości koniec,
instrukcja jest wykonywana. Za każdym

razem wartość zmiennej zmniejszana
jest o 1. Gdy wartość zmiennej zm staje

się mniejsza od wartości koniec
sterowanie jest przenoszone do
kolejnych instrukcji po instrukcji FOR.

●

instrukcja może być instrukcją złożoną

{ }.

Krzysztof Pancerz

Algorytmy i struktury danych

Wczytywanie i wypisywanie danych

cin>>zmienna;

cout<<zmienna;

cin – standardowy strumień wejściowy
(klawiatura)
cout – standardowy strumień wyjściowy (ekran
terminala)

Krzysztof Pancerz

Algorytmy i struktury danych

Struktura najprostszego programu w języku C/C++

void main( )

{

// ... instrukcje do wykonania ...

}

Krzysztof Pancerz

Algorytmy i struktury danych

Podstawowe struktury algorytmów

●

Algorytmy liniowe.

●

Algorytmy z rozgałęzieniami.

●

Algorytmy cykliczne (z pętlami).

Krzysztof Pancerz

Algorytmy i struktury danych

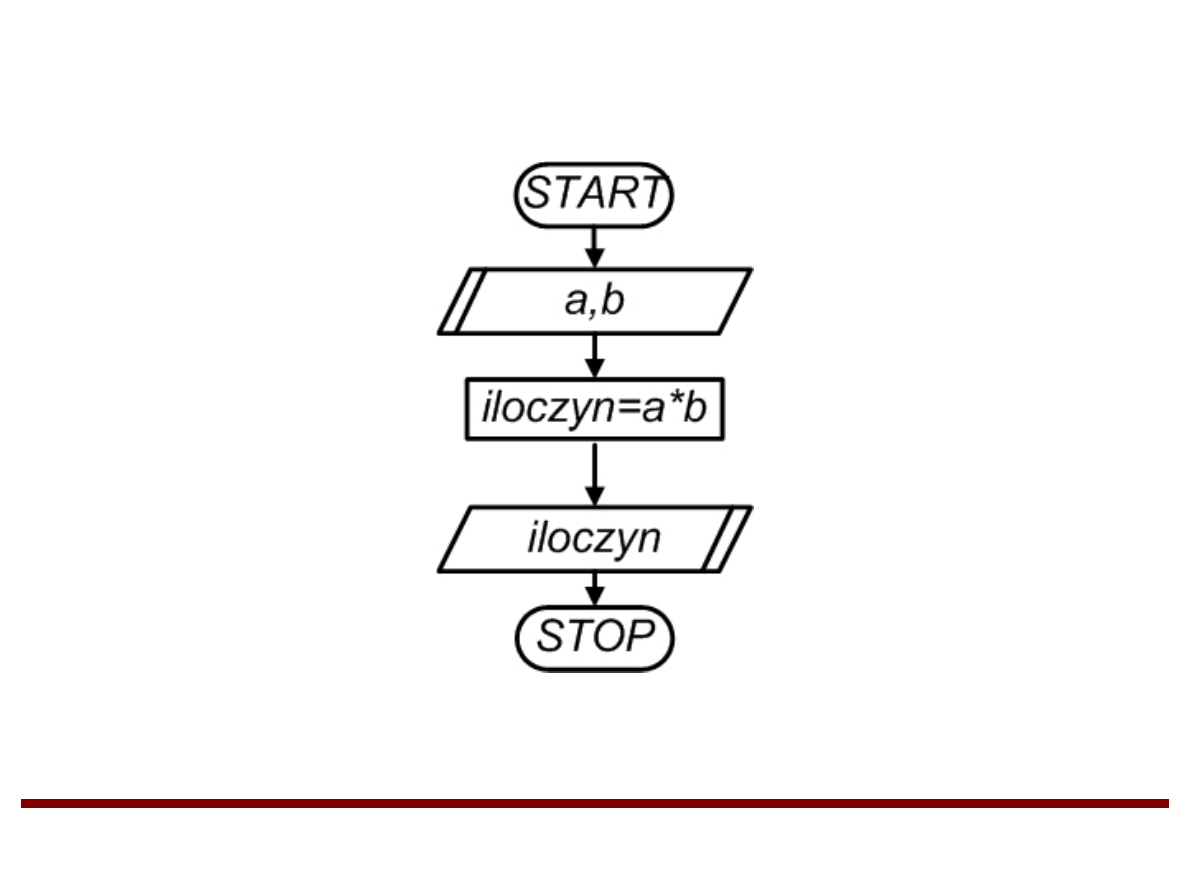
Przykład 1 (algorytm liniowy)

●

Napisać algorytm mnożenia dwóch liczb
całkowitych.

Krzysztof Pancerz

Algorytmy i struktury danych

Rozwiązanie przykładu 1

Krzysztof Pancerz

Algorytmy i struktury danych

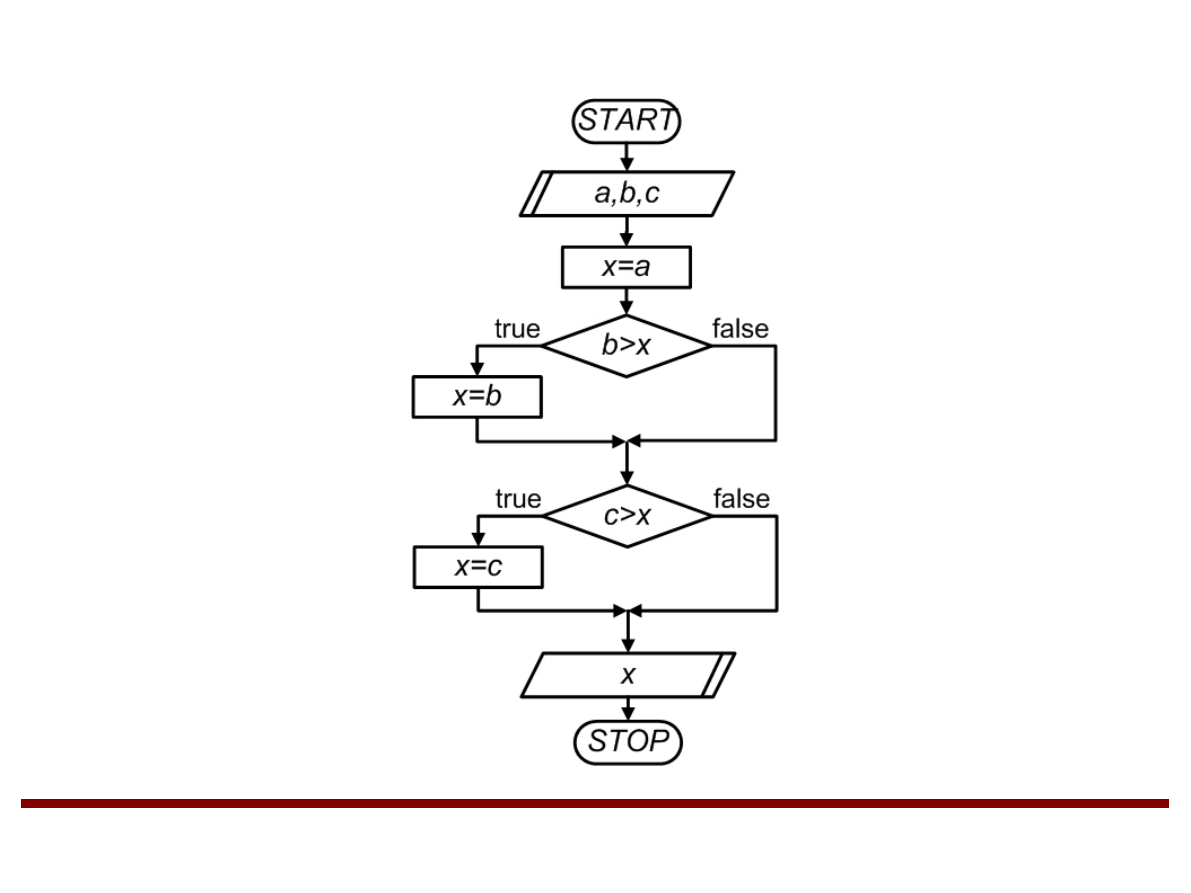
Przykład 2 (algorytm z rozgałęzieniami)

●

Napisać algorytm znajdujący maksymalną z
trzech liczb rzeczywistych a, b oraz c.

Krzysztof Pancerz

Algorytmy i struktury danych

Rozwiązanie przykładu 2

Krzysztof Pancerz

Algorytmy i struktury danych

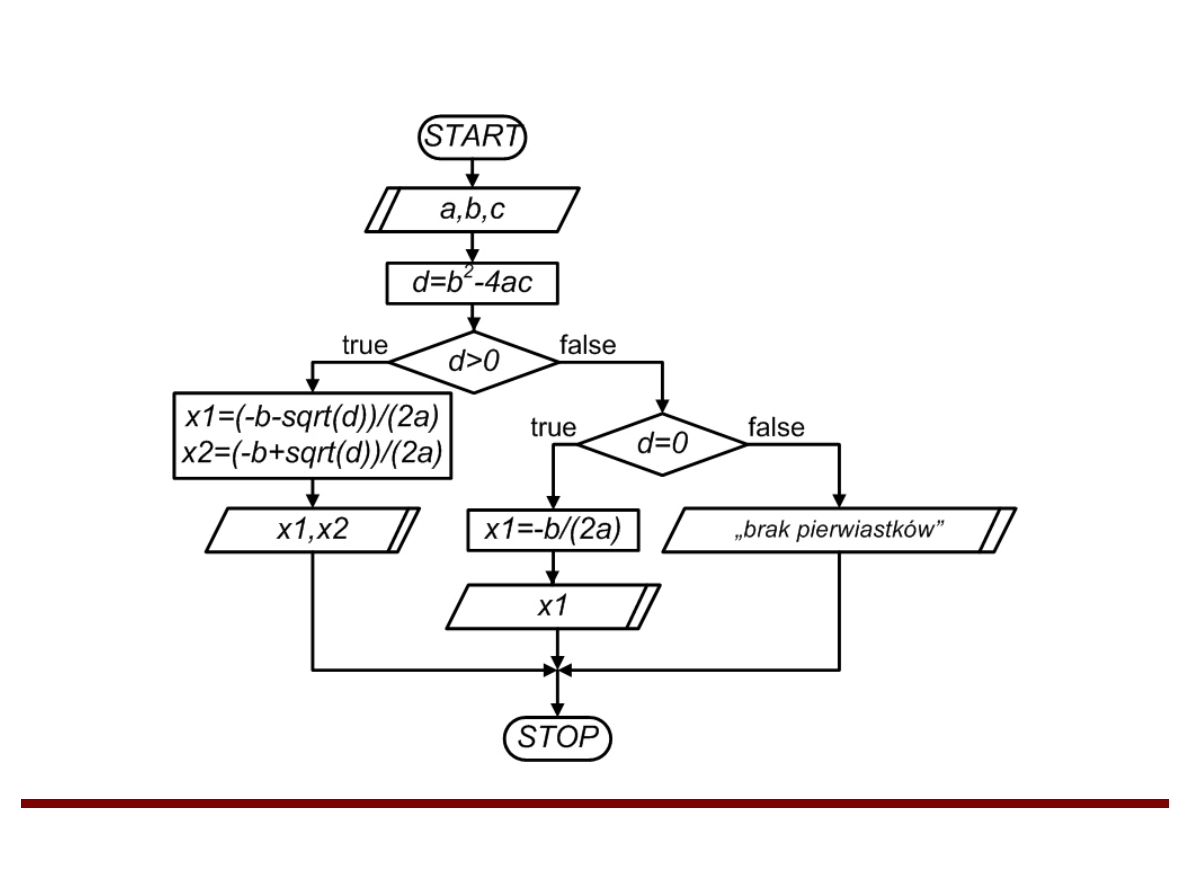
Przykład 3 (algorytm z rozgałęzieniami)

●

Napisać algorytm rozwiązujący równanie
kwadratowe:

ax

2

+bx+c=0

przy założeniu, że a≠0.

Krzysztof Pancerz

Algorytmy i struktury danych

Rozwiązanie przykładu 3

Krzysztof Pancerz

Algorytmy i struktury danych

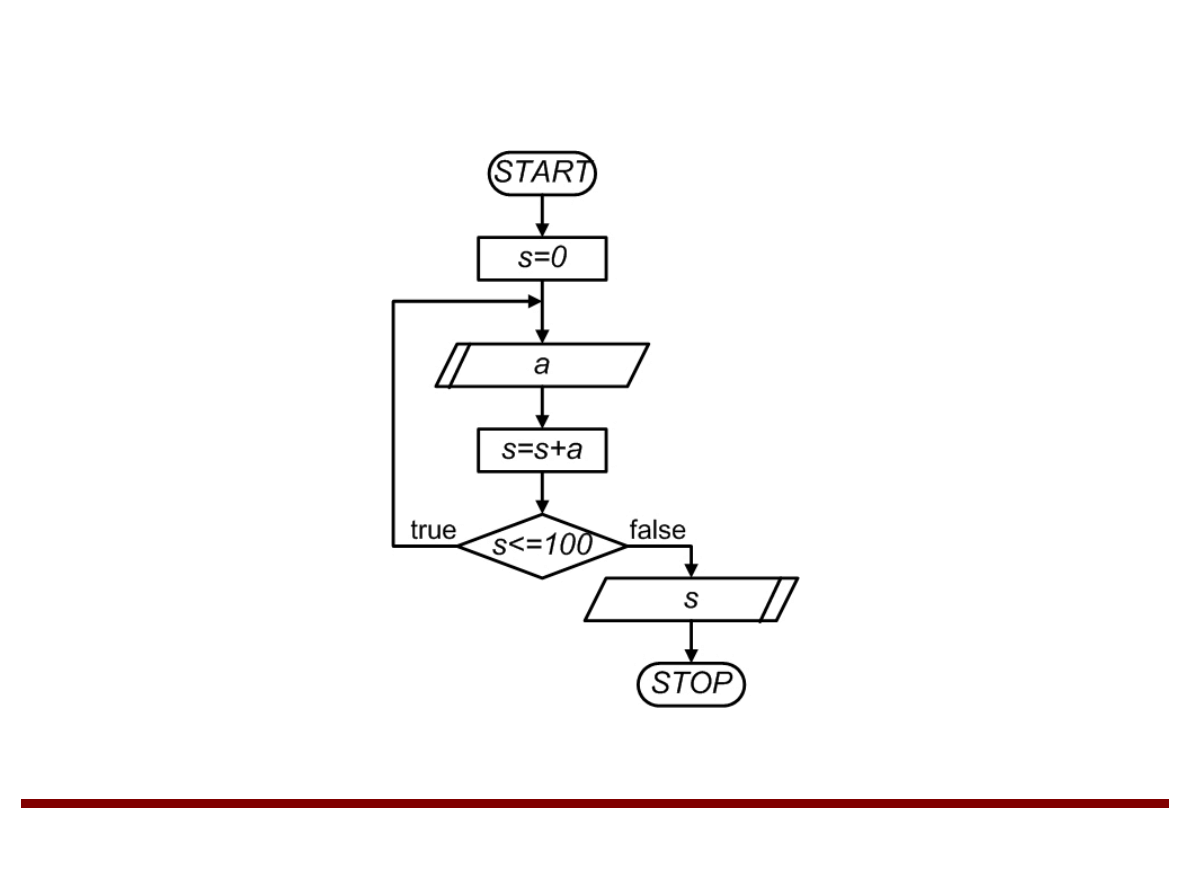
Przykład 4 (algorytm cykliczny)

●

Napisać algorytm dodający liczby całkowite
podawane przez użytkownika aż do momentu
gdy ich suma przekroczy wartość 100.

Krzysztof Pancerz

Algorytmy i struktury danych

Rozwiązanie przykładu 4

Krzysztof Pancerz

Algorytmy i struktury danych

Tablice

●

Tablica jest zbiorem elementów tego samego
typu.

●

Każdy element jest identyfikowany przez indeks
(numer pozycji na której się znajduje).

●

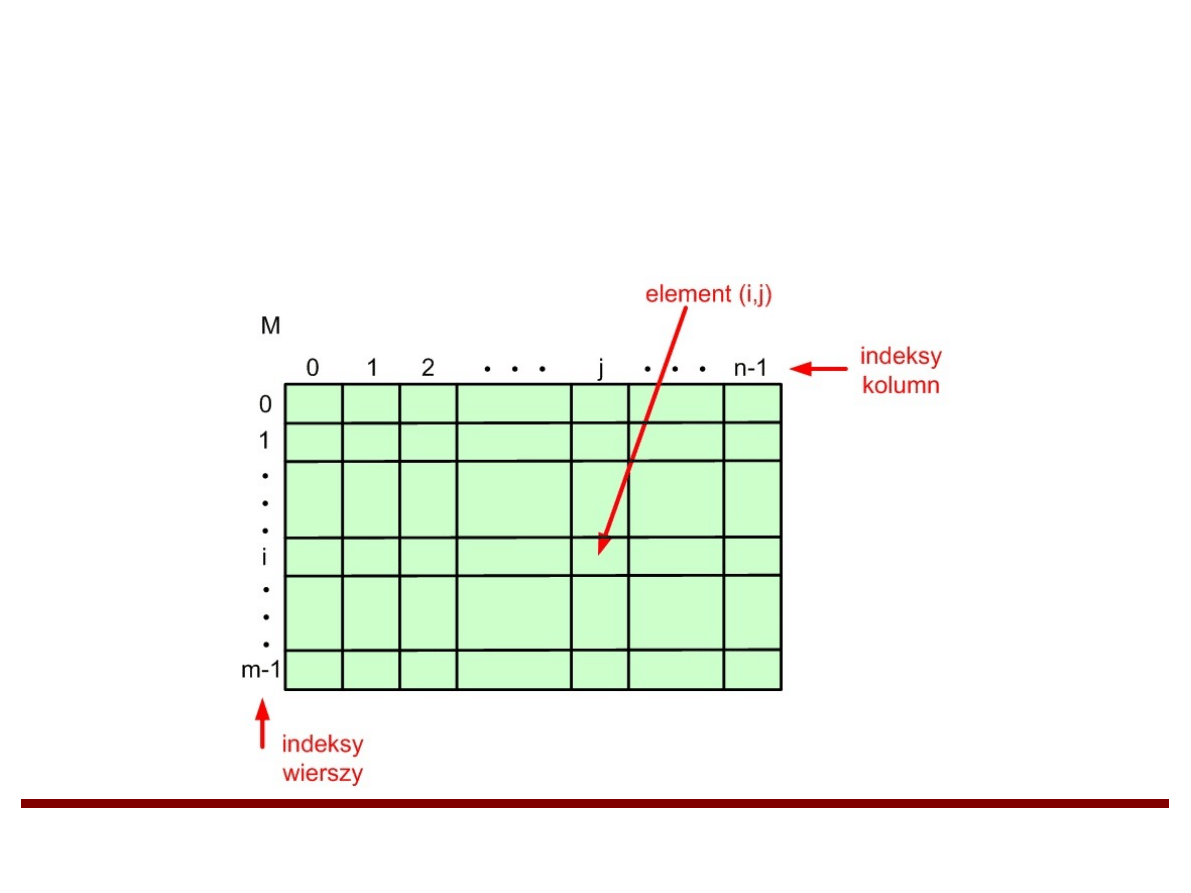
W pamięci komputera tablica zajmuje ciągły
obszar komórek pamięci.

●

Tablica charakteryzuje się bezpośrednim
dostępem do elementów. Dostęp ten uzyskuje
się poprzez podanie odpowiednich indeksów
elementów.

Krzysztof Pancerz

Algorytmy i struktury danych

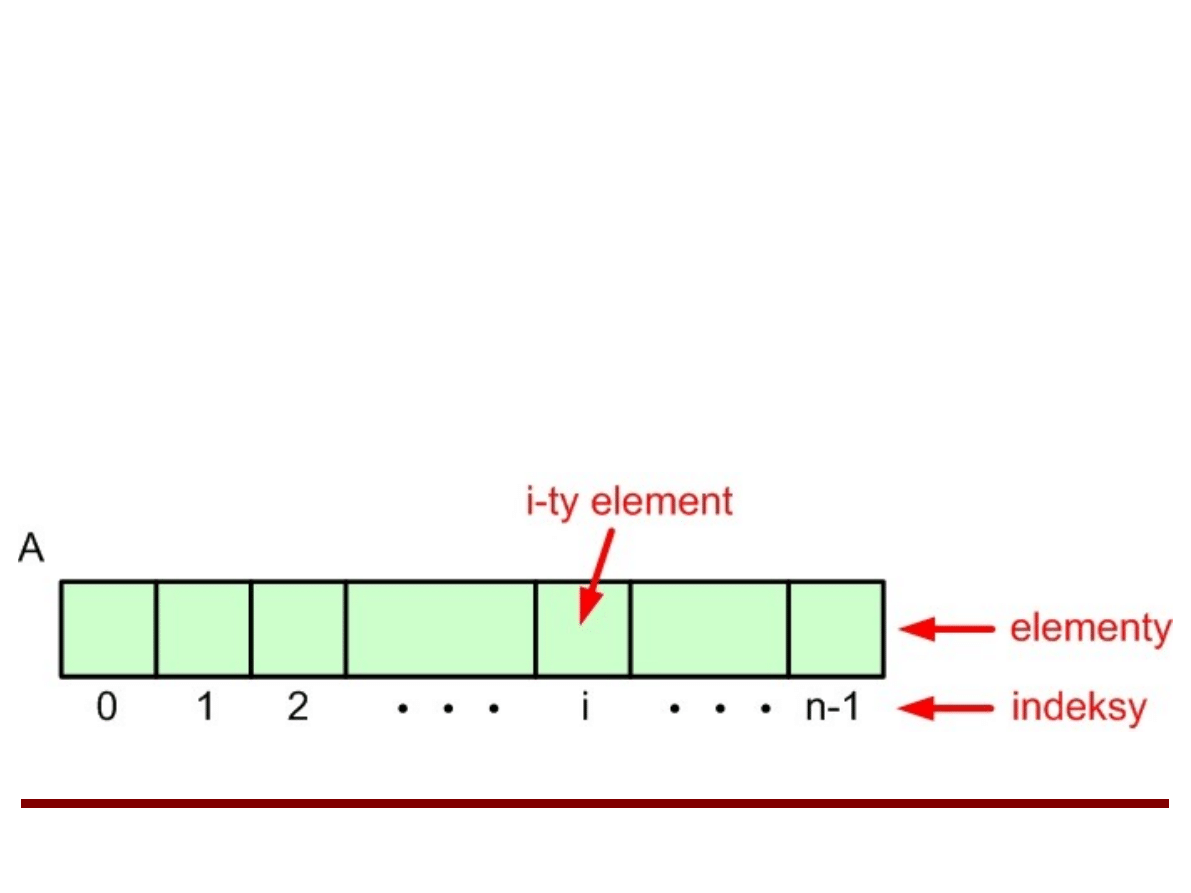
Tablice jednowymiarowe

●

A – nazwa tablicy

●

n – maksymalna liczba elementów, które mogą
być przechowywane w tablicy (rozmiar tablicy).

●

i-ty element jest przechowywany w tablicy w
komórce o indeksie i.

Krzysztof Pancerz

Algorytmy i struktury danych

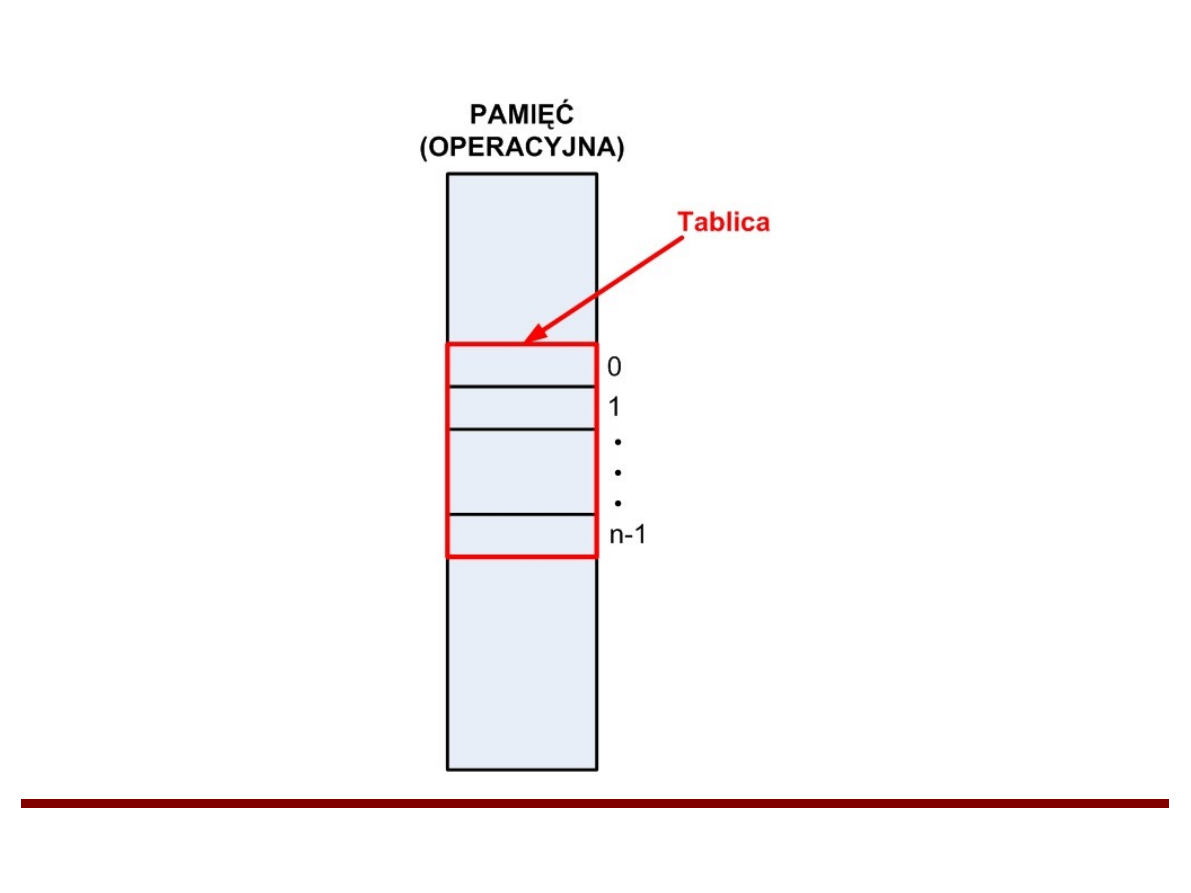
Tablice jednowymiarowe (cd.)

●

Numeracja pozycji rozpoczyna się zawsze
od zera w języku C/C++, tj. indeksem
pierwszego elementu jest 0, następnego 1, itd.

Krzysztof Pancerz

Algorytmy i struktury danych

Tablica w pamięci komputera

Krzysztof Pancerz

Algorytmy i struktury danych

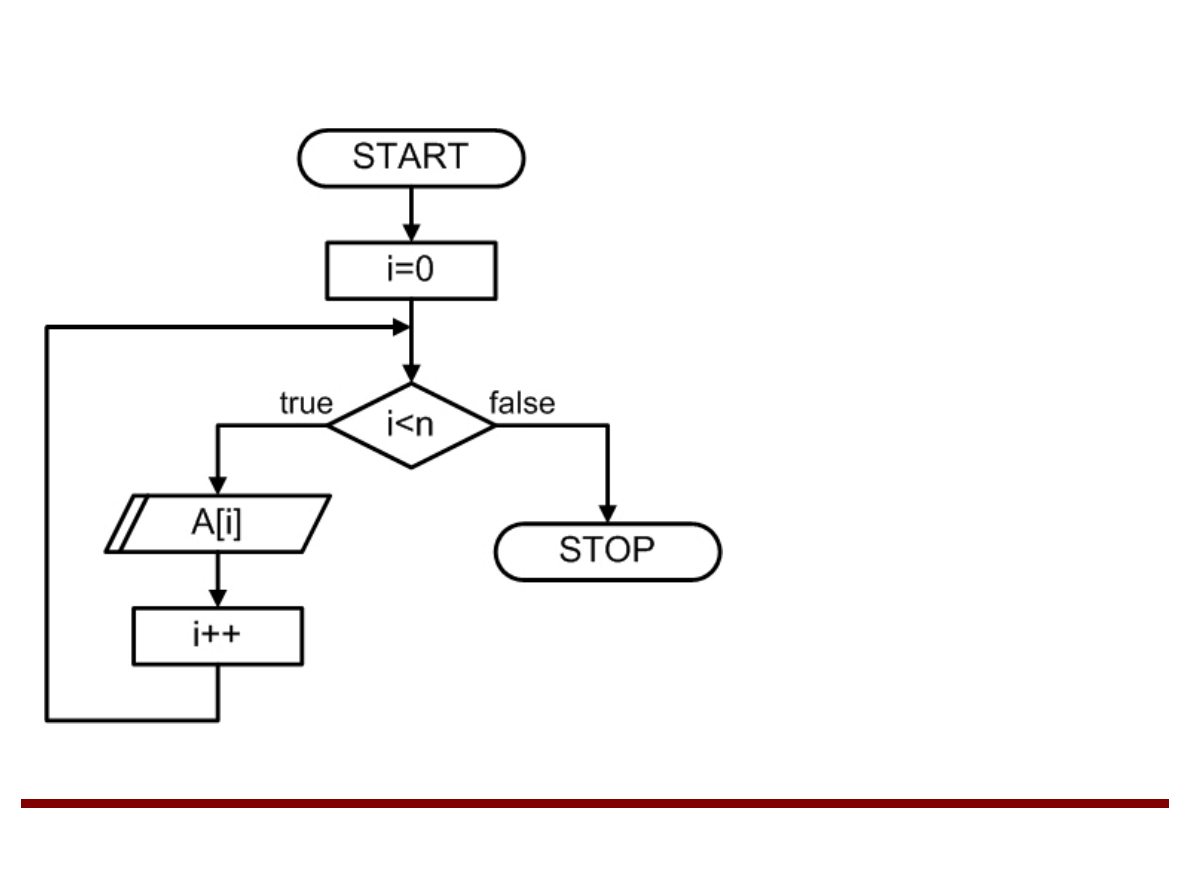
Tablice dwuwymiarowe

●

Każdy element w tablicy dwuwymiarowej jest
identyfikowany przez dwa indeksy (indeks
wiersza oraz indeks kolumny).

Krzysztof Pancerz

Algorytmy i struktury danych

Tablice jednowymiarowe w języku C/C++

●

Deklaracja tablicy o ustalonym rozmiarze

typ_elementów nazwa_tablicy[rozmiar];

●

Przykłady

int A[50];
char znaki[100];

Krzysztof Pancerz

Algorytmy i struktury danych

Tablice jednowymiarowe w języku C/C++(cd.)

●

Inicjalizacja tablic

Przykład
int tab[ ]={1, -5, 0, 34};

●

Odwołanie do elementów tablicy

nazwa_tablicy[indeks_elementu];
Przykłady
A[5];
znaki[0];

●

Określenie rozmiaru tablicy w bajtach

sizeof(nazwa_tablicy);

Krzysztof Pancerz

Algorytmy i struktury danych

Tablice dwuwymiarowe w języku C/C++

●

Deklaracja tablicy dwuwymiarowej o ustalonym
rozmiarze:

typ_elementów nazwa_tablicy[liczba_wierszy]

[liczba_kolumn];

●

Przykłady

float macierz[50][100];
char a[5][5];

Krzysztof Pancerz

Algorytmy i struktury danych

Tablice dwuwymiarowe w języku C/C++

●

Inicjalizacja tablicy

Przykład
char tab[ ][ ]={ {'a', 'b', 'c'}, {'d', 'e', 'f'} };

●

Odwołanie do elementów tablicy

nazwa_tablicy[indeks_wiersza][indeks_kolumny];
Przykłady
macierz[5][8];
a[0][0];

Krzysztof Pancerz

Algorytmy i struktury danych

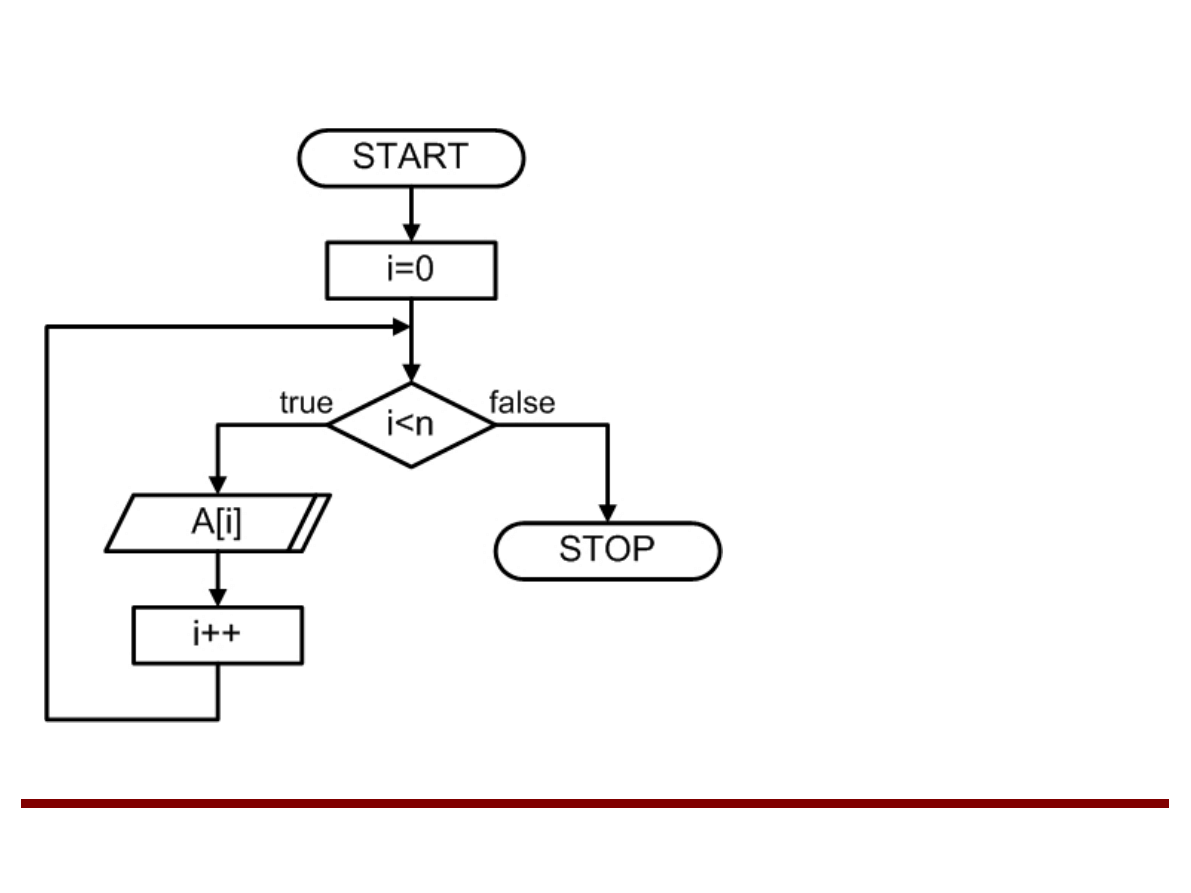
Wczytywanie elementów tablicy jednowymiarowej

A – tablica o rozmiarze n

Krzysztof Pancerz

Algorytmy i struktury danych

Wypisywanie elementów tablicy jednowymiarowej

A – tablica o rozmiarze n

Krzysztof Pancerz

Algorytmy i struktury danych

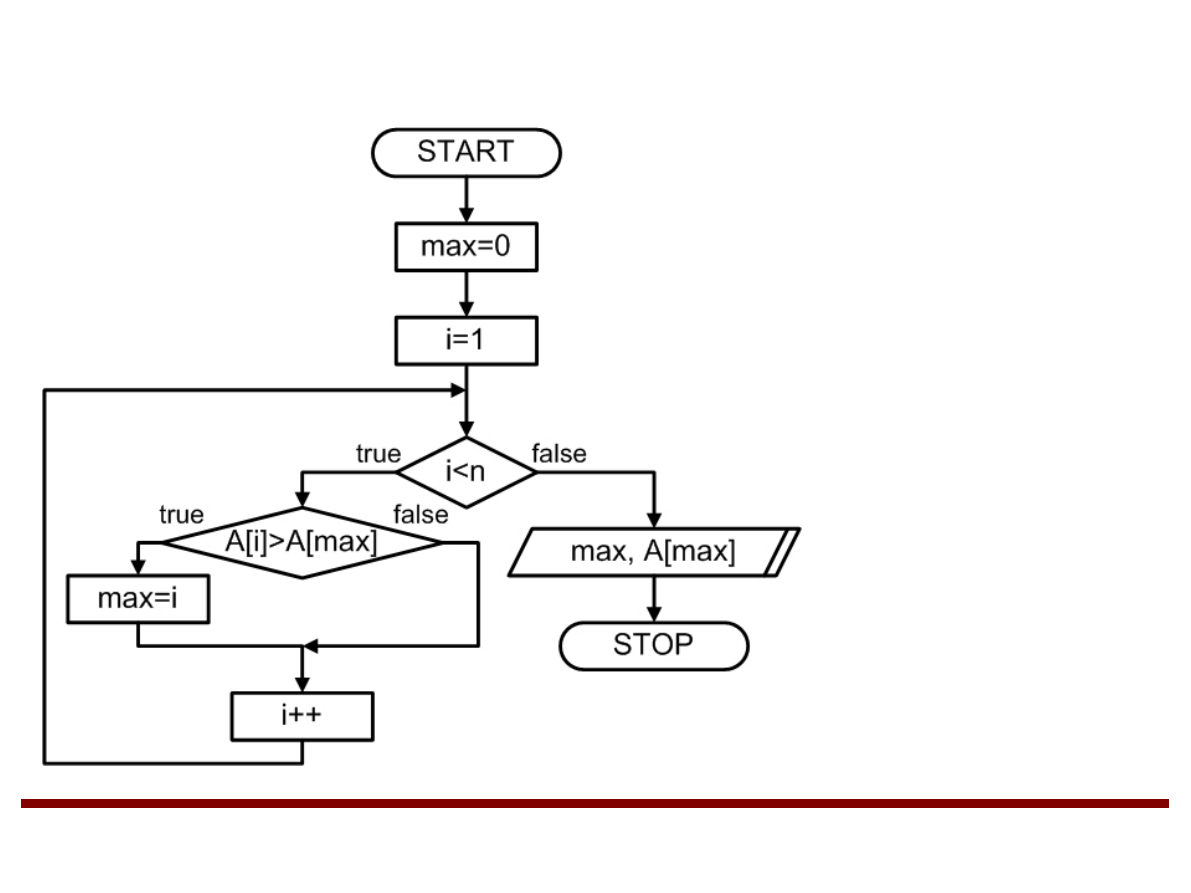
Wyszukiwanie największego elementu w tablicy

jednowymiarowej

A – tablica o rozmiarze n

max – indeks aktualnie
największego elementu
w tablicy

Krzysztof Pancerz

Algorytmy i struktury danych

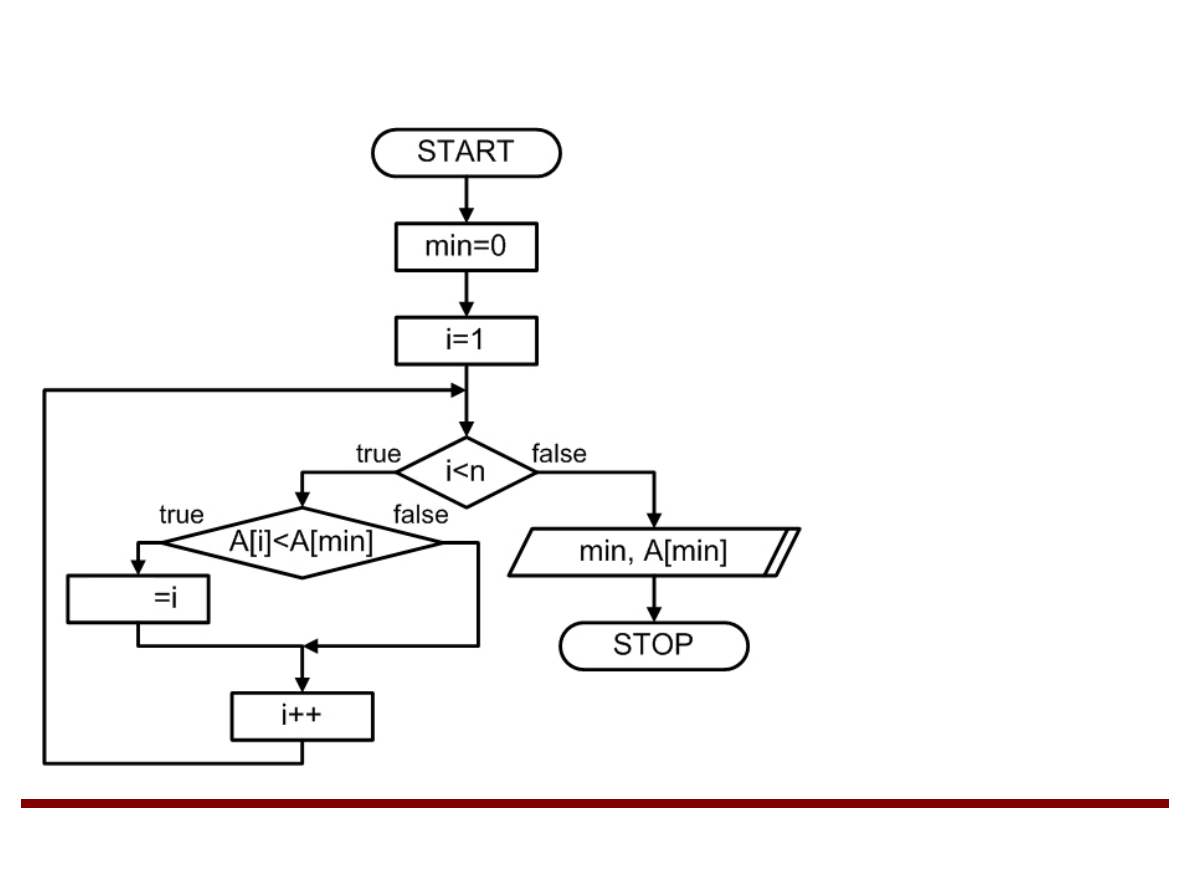
Wyszukiwanie najmniejszego elementu w tablicy

jednowymiarowej

A – tablica o rozmiarze n

min – indeks aktualnie
najmniejszego elementu
w tablicy

min

Krzysztof Pancerz

Algorytmy i struktury danych

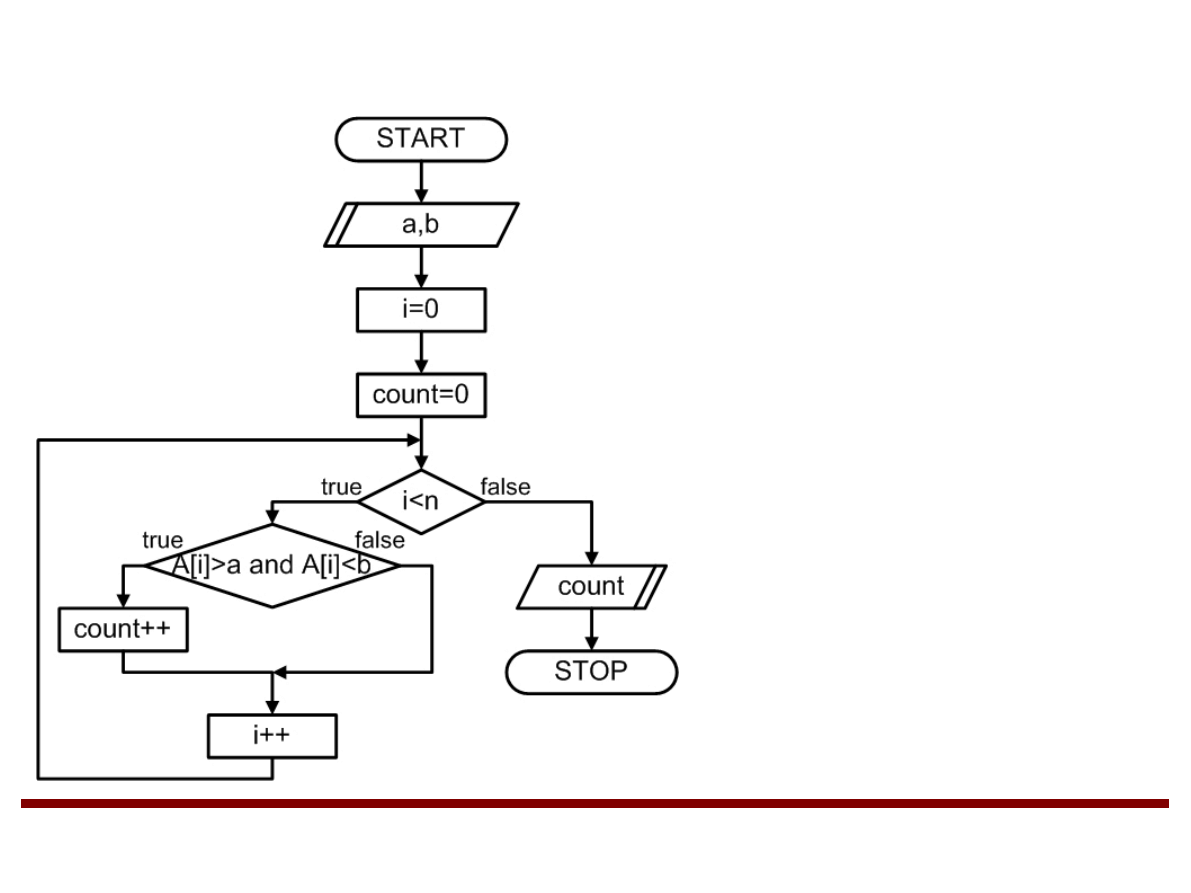
Zliczanie elementów tablicy jednowymiarowej

należących do danego przedziału

A – tablica o rozmiarze n

a – lewy kraniec
przedziału

b – prawy kraniec
przedziału

Krzysztof Pancerz

Algorytmy i struktury danych

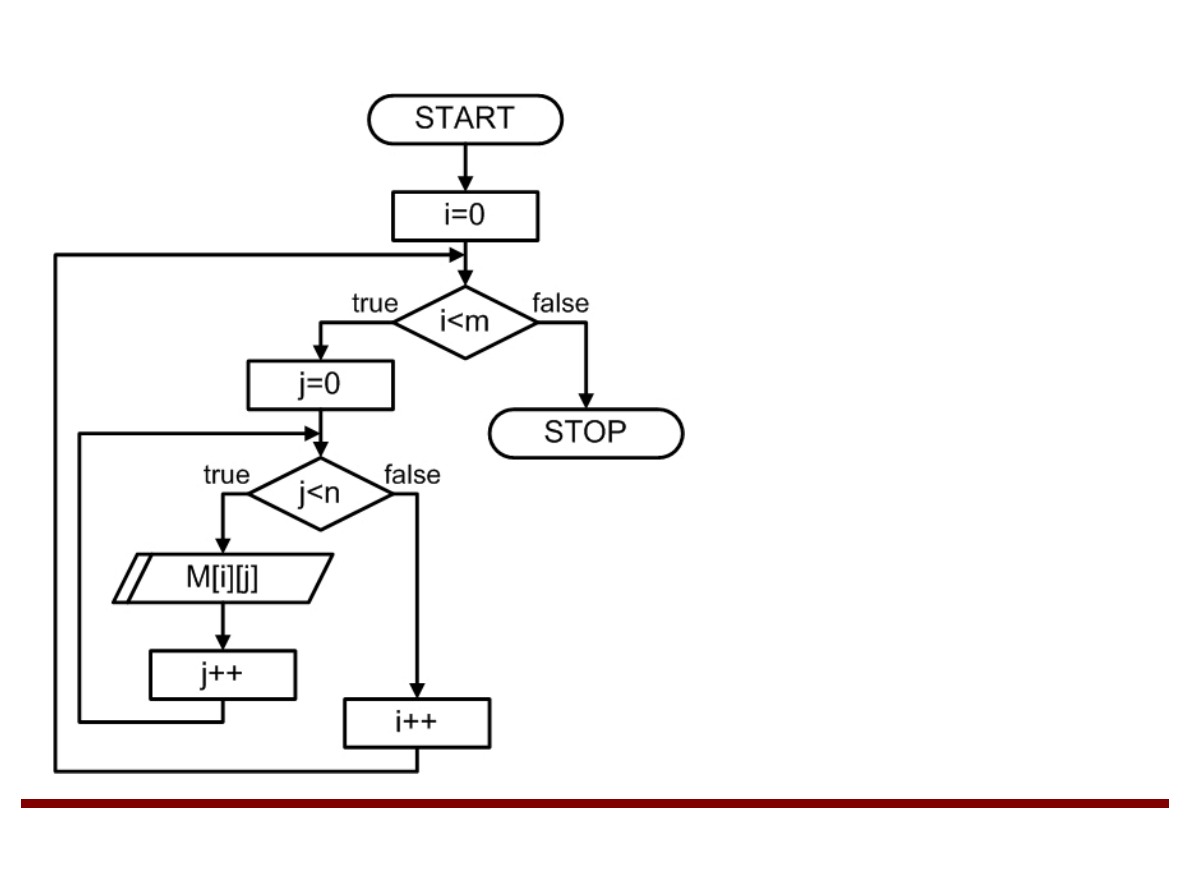
Wczytywanie elementów tablicy dwuwymiarowej

M – tablica (macierz) o
rozmiarze m×n

Krzysztof Pancerz

Algorytmy i struktury danych

Grafy

Graf (lub graf nieskierowany) G składa się z

niepustego skończonego zbioru wierzchołków
(węzłów) V oraz skończonego zbioru krawędzi E
będących nieuporządkowanymi parami elementów
ze zbioru V.

Krzysztof Pancerz

Algorytmy i struktury danych

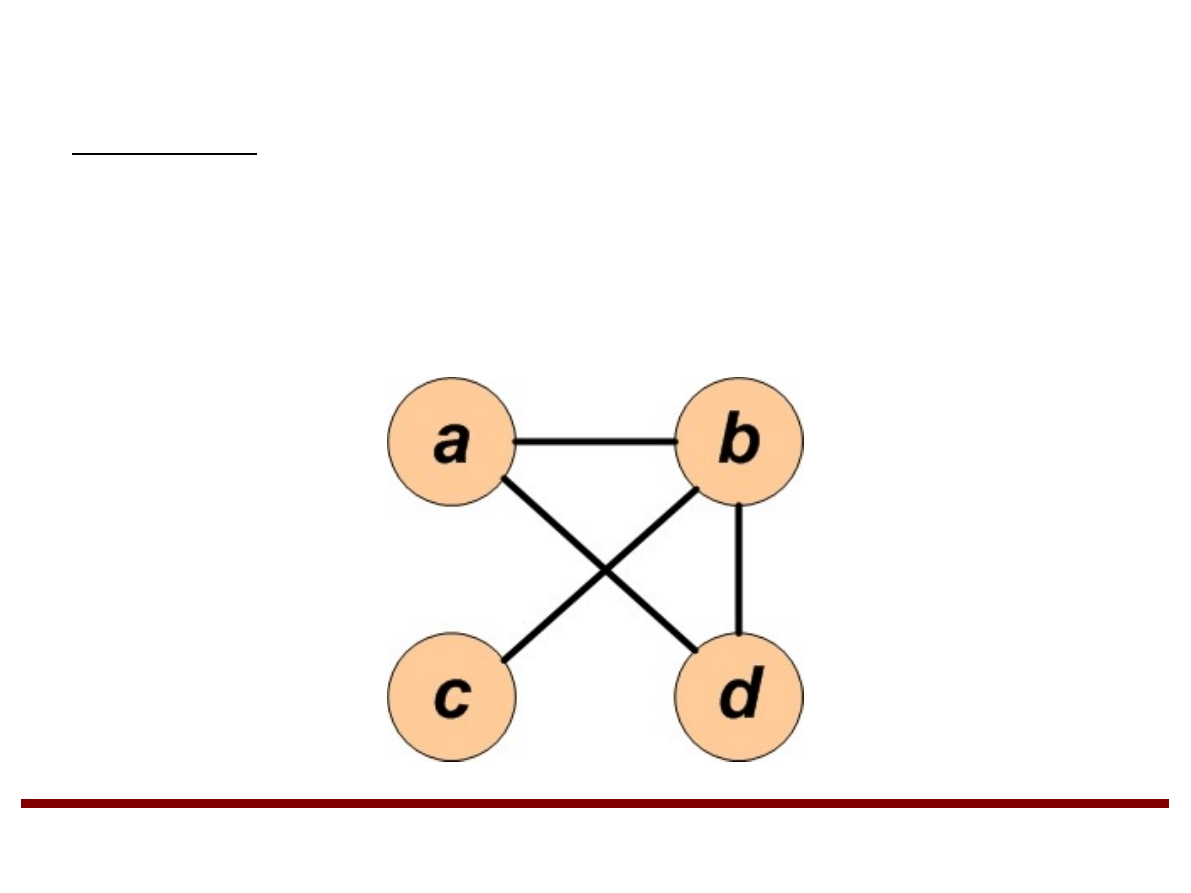
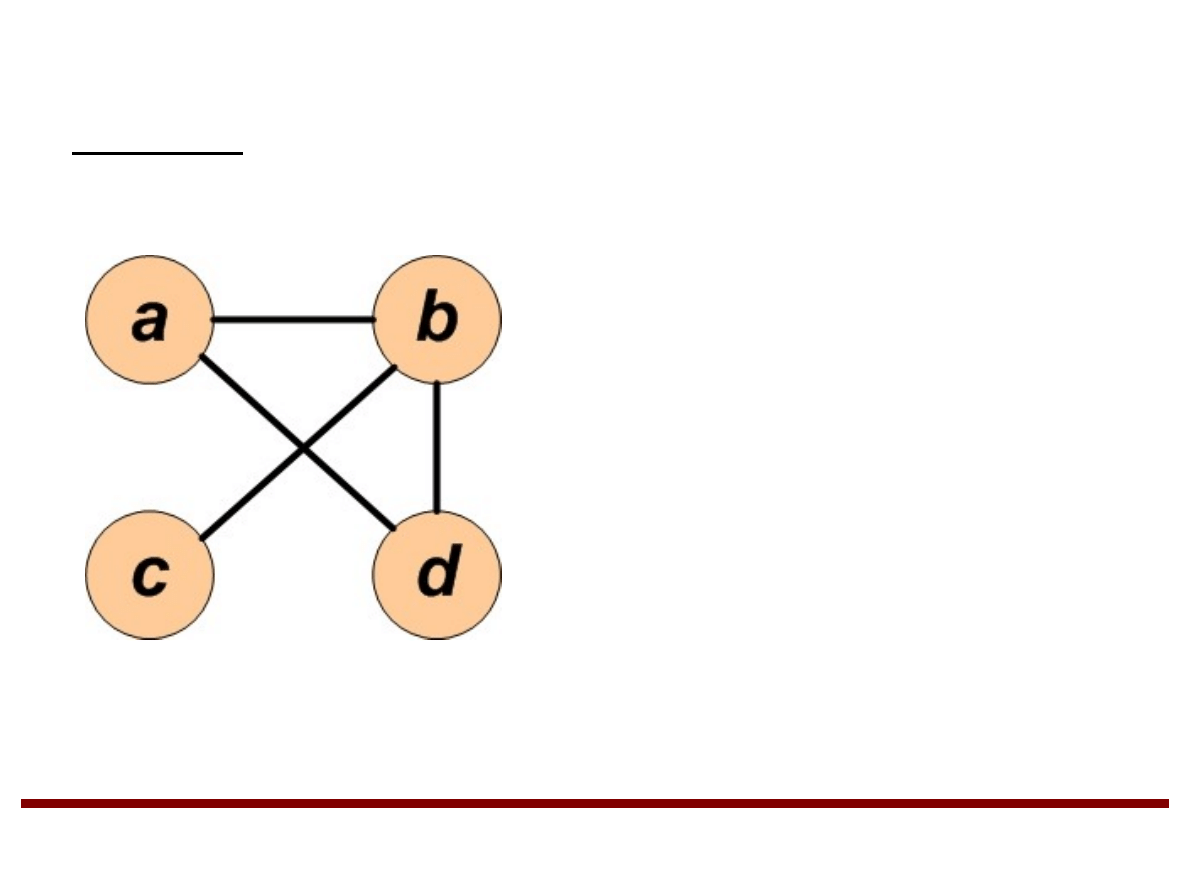
Grafy (cd.)

Przykład

G=V , E 
V ={a , b , c , d }

E={a , b ,b , c ,b , d  ,a , d }

Krzysztof Pancerz

Algorytmy i struktury danych

Grafy (cd.)

Graf skierowany G składa się z niepustego

skończonego zbioru wierzchołków (węzłów) V oraz
skończonego zbioru krawędzi E będących
uporządkowanymi parami elementów ze zbioru V.

Krzysztof Pancerz

Algorytmy i struktury danych

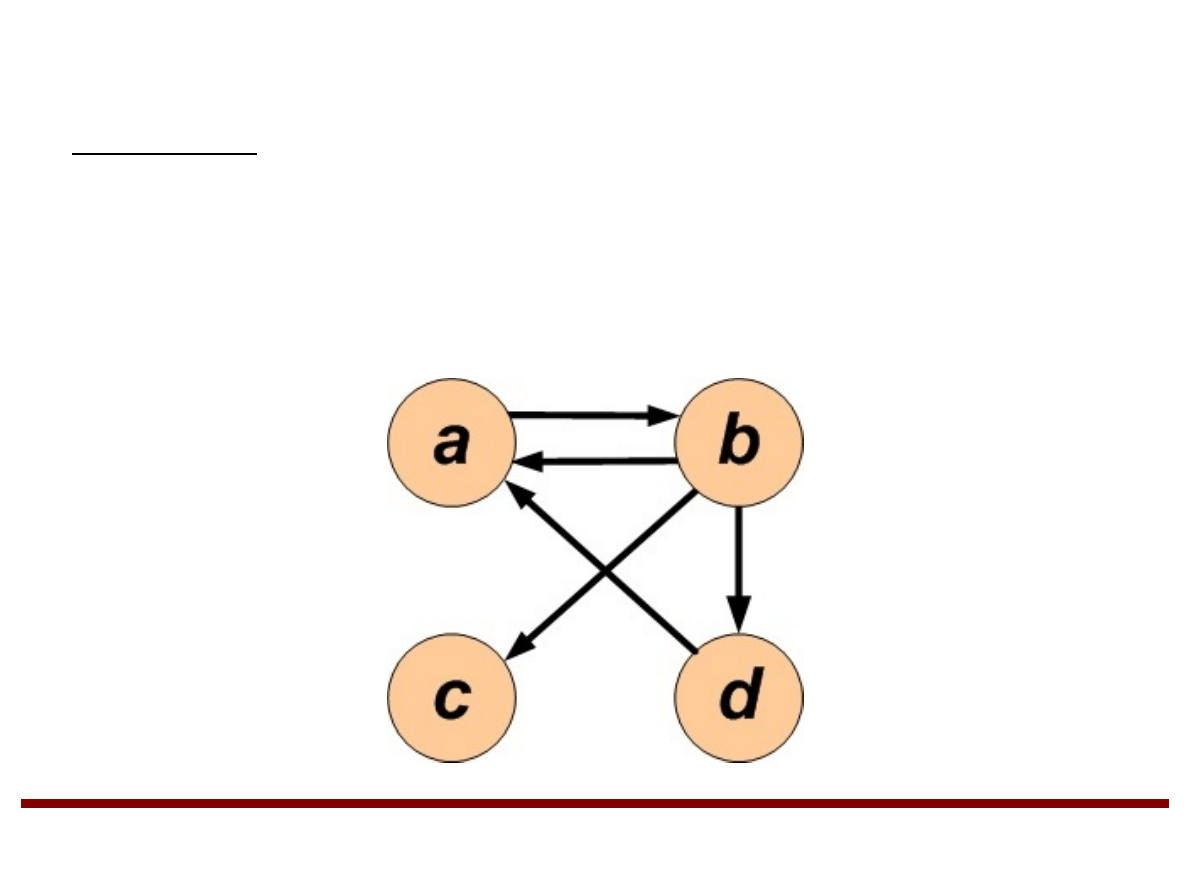
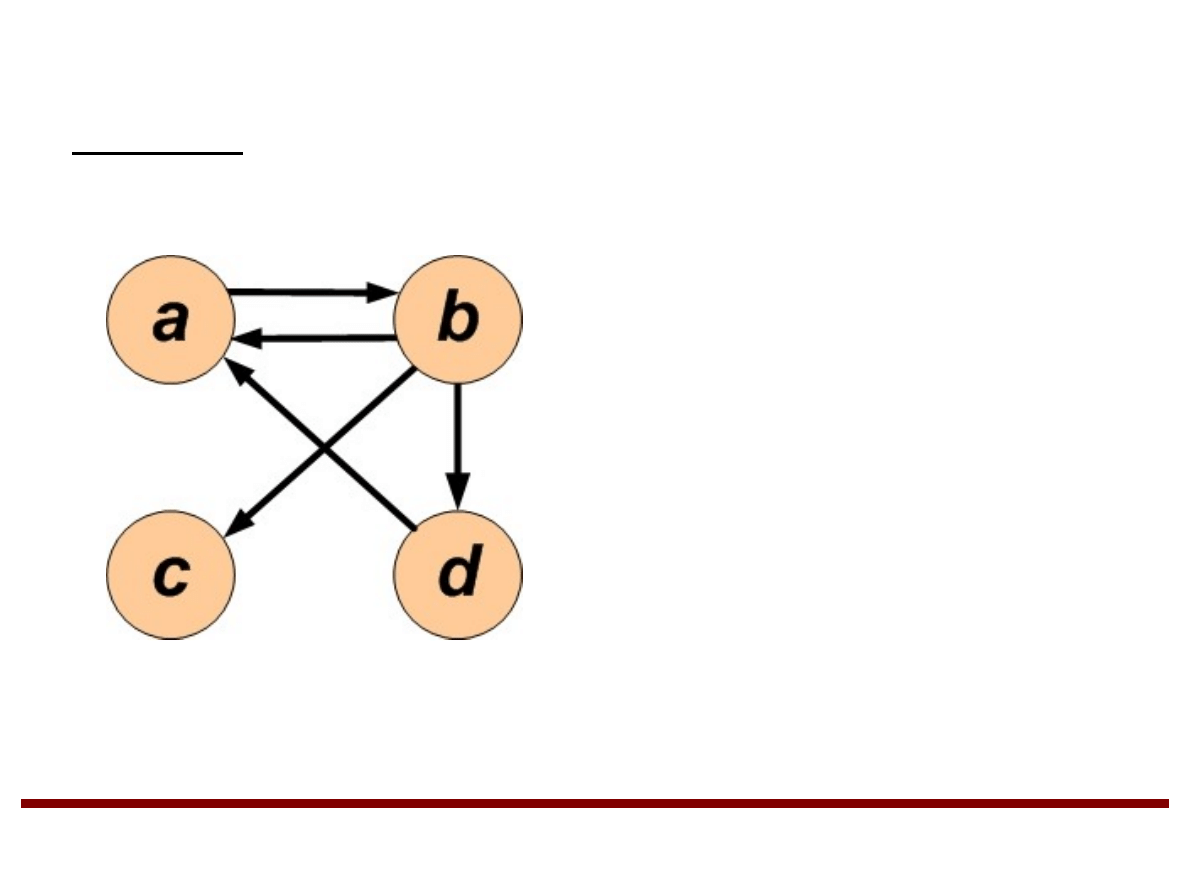
Grafy (cd.)

Przykład

G=V , E 
V ={a , b , c , d }

E={a , b ,b , a ,b , c ,b , d  ,d , a}

Krzysztof Pancerz

Algorytmy i struktury danych

Grafy (cd.)

●

Krawędź (i,j), gdzie i oraz j są wierzchołkami,
nazywa się krawędzią incydentną z wierzchołkami
i oraz j.

●

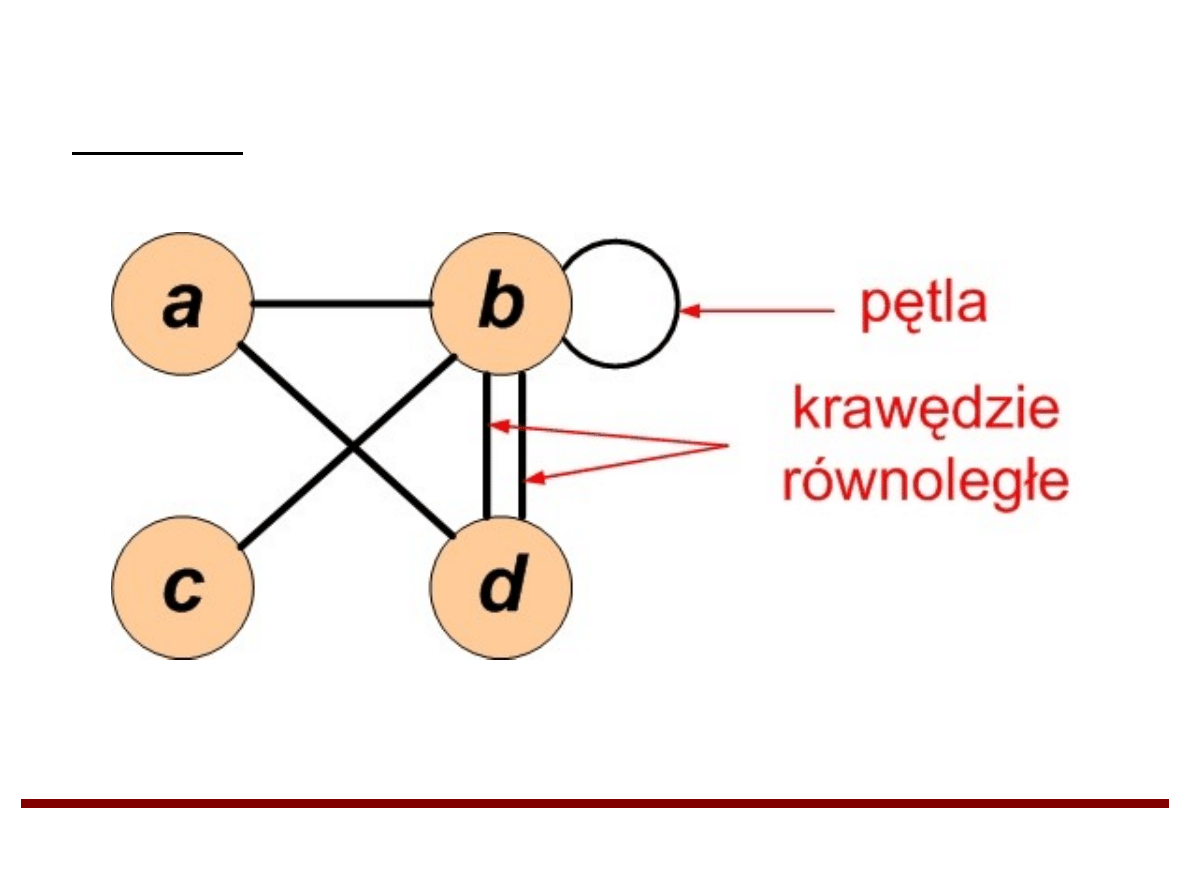
Krawędź (i,i) incydentna z pojedynczym
wierzchołkiem i nazywana jest pętlą.

●

Krawędzie incydentne z wierzchołkami i oraz j,
gdzie i≠j, nazywane są krawędziami
równoległymi.

●

Grafem prostym nazywany jest graf, który nie
zawiera zarówno pętli jak i krawędzi równoległych.

Krzysztof Pancerz

Algorytmy i struktury danych

Grafy (cd.)

Przykład

Krzysztof Pancerz

Algorytmy i struktury danych

Reprezentacja grafów

Macierz sąsiedztwa

●

Wiersze i kolumny macierzy sąsiedztwa m
etykietowane są uporządkowanymi parami
wierzchołków.

●

Jeśli (i,j) jest krawędzią, to m(i,j)=1.

●

Jeśli (i,j) nie jest krawędzią, to m(i,j)=0.

Krzysztof Pancerz

Algorytmy i struktury danych

Reprezentacja grafów

Przykład

m=

[

0 1 0 1
1 0 1 1
0 1 0 0
1 1 0 0

]

Krzysztof Pancerz

Algorytmy i struktury danych

Reprezentacja grafów

Przykład

m=

[

0 1 0 0
1 0 1 1
0 0 0 0
1 0 0 0

]

Krzysztof Pancerz

Algorytmy i struktury danych

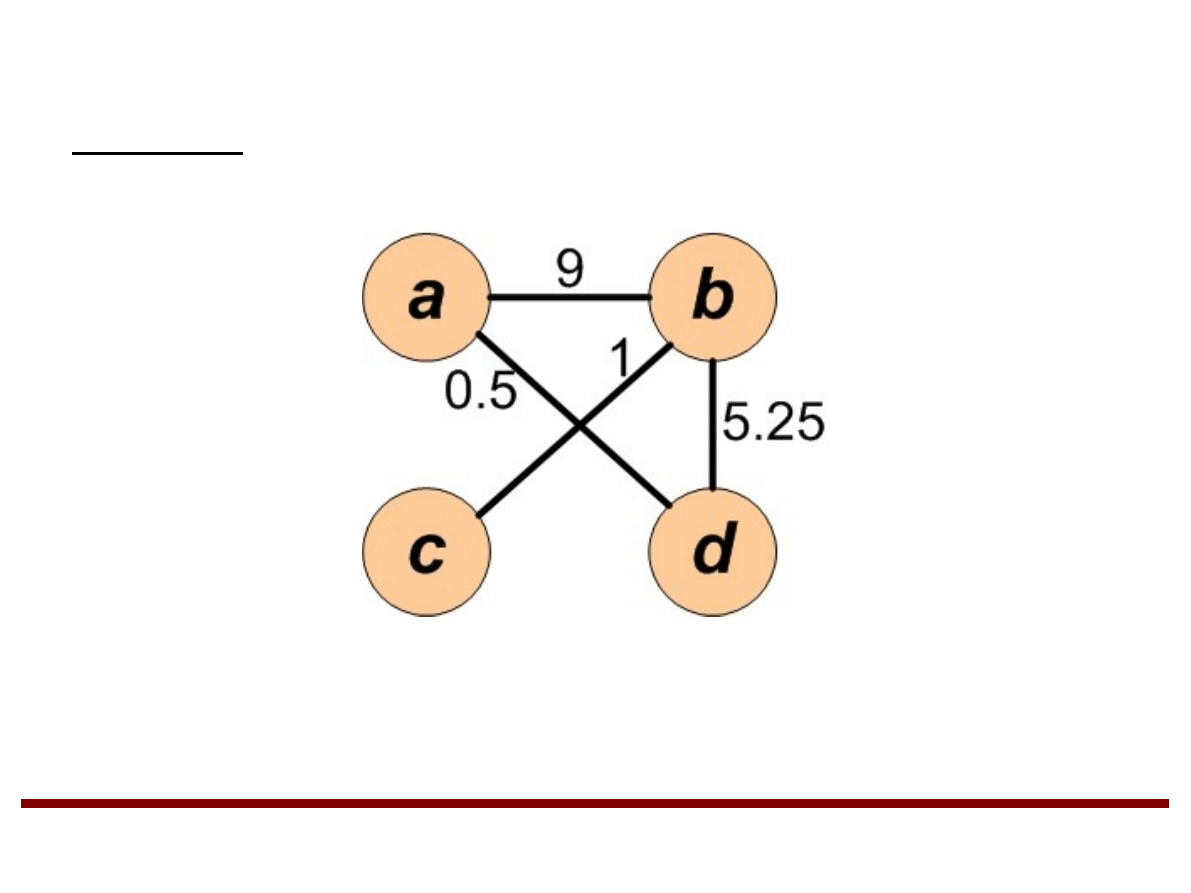
Grafy (cd.)

Graf z wagami (skierowany lub nieskierowany) G

składa się ze zbioru wierzchołków V, zbioru
krawędzi E oraz funkcji wagowej w
przyporządkowującej każdej krawędzi ze zbioru E
liczbę rzeczywistą.

●

Wartość dla jest nazywana wagą lub
kosztem krawędzi e.

w e

e∈E

Krzysztof Pancerz

Algorytmy i struktury danych

Grafy (cd.)

Przykład

Krzysztof Pancerz

Algorytmy i struktury danych

Grafy (cd.)

Niech u oraz v będą wierzchołkami grafu. Ścieżką z u

do v długości n nazywamy ciąg n+1 wierzchołków
oraz n krawędzi o początku w wierzchołku u i końcu
w wierzchołku v:

Ścieżka prosta z u do v jest ścieżką z u do v bez

powtarzających się wierzchołków.

Cykl jest ścieżką o niezerowej długości z wierzchołka

v do tego samego wierzchołka v bez powtarzających
się krawędzi.



u , e

1

, v

1

,e

2

, v

2

,... , v

n−1

, e

n

, v

Krzysztof Pancerz

Algorytmy i struktury danych

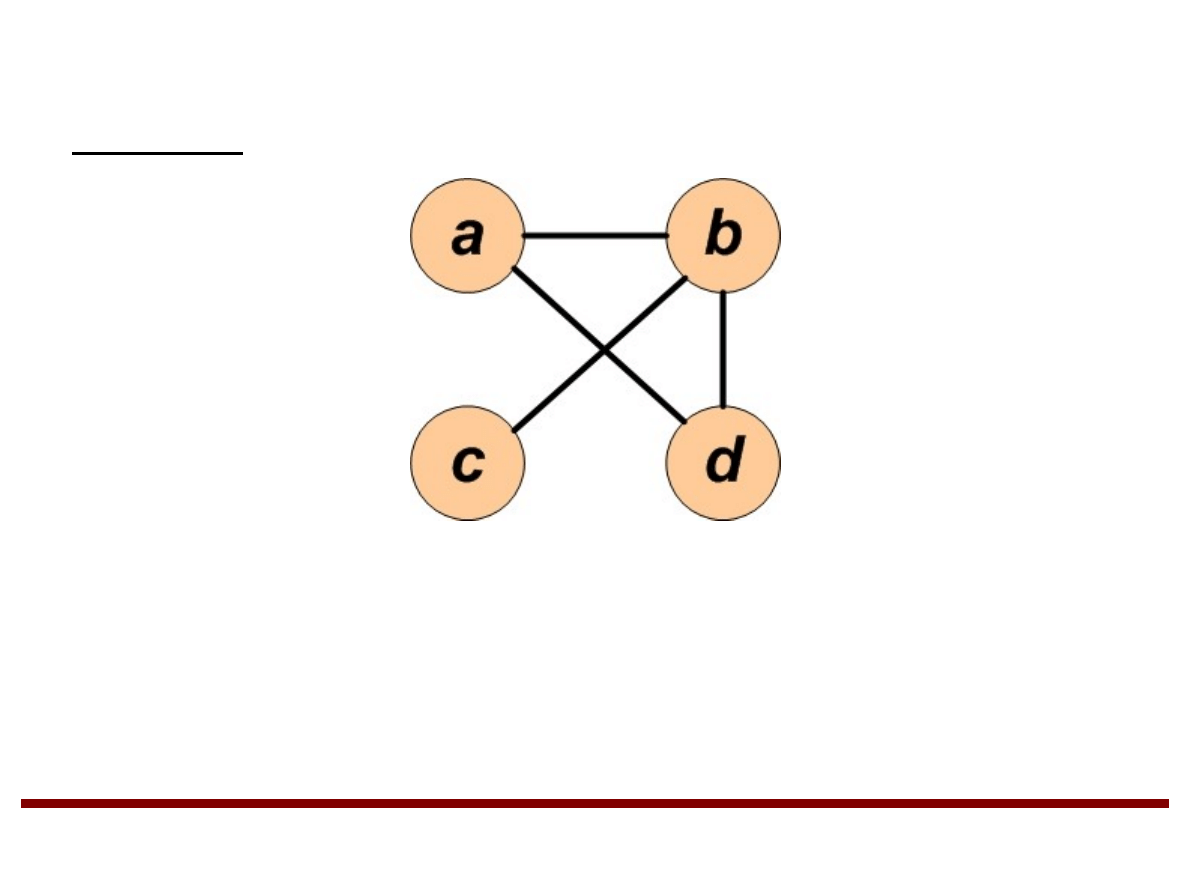
Grafy (cd.)

Przykład

Ścieżka: (a, (a,b), b, (b,d), d)
Cykl: (a, (a,b), b, (b,d), d, (d,a), a)

Krzysztof Pancerz

Algorytmy i struktury danych

Grafy (cd.)

Graf spójny jest grafem w którym istnieje ścieżka z u

do v dla każdego wierzchołka u oraz v.

Graf acykliczny jest grafem, który nie zawiera cykli.

Krzysztof Pancerz

Algorytmy i struktury danych

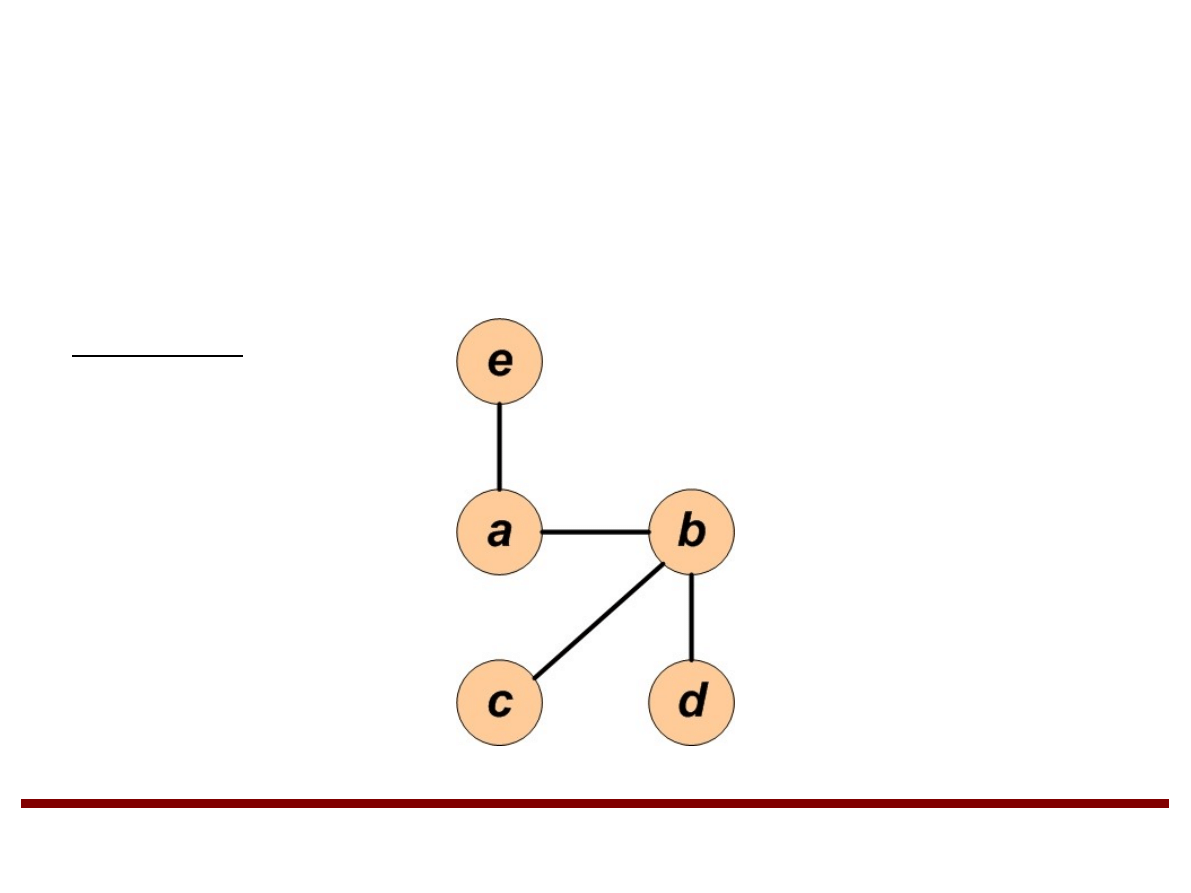
Drzewa

Drzewo (lub drzewo wolne) T jest grafem prostym,

który jest acykliczny i spójny.

Przykład

Krzysztof Pancerz

Algorytmy i struktury danych

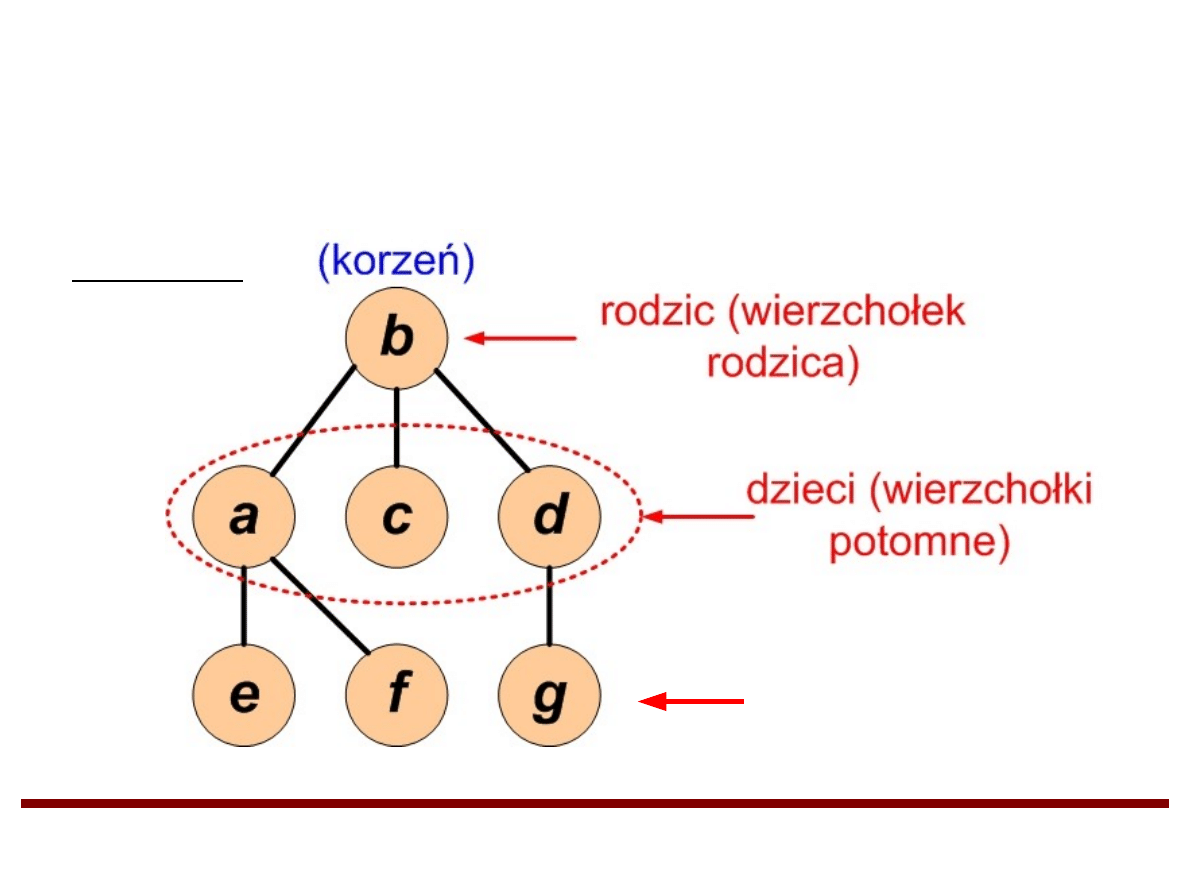
Drzewa (cd.)

Drzewo z korzeniem jest drzewem z wyróżnionym

jednym wierzchołkiem nazywanym korzeniem.

Przykład

liście

Krzysztof Pancerz

Algorytmy i struktury danych

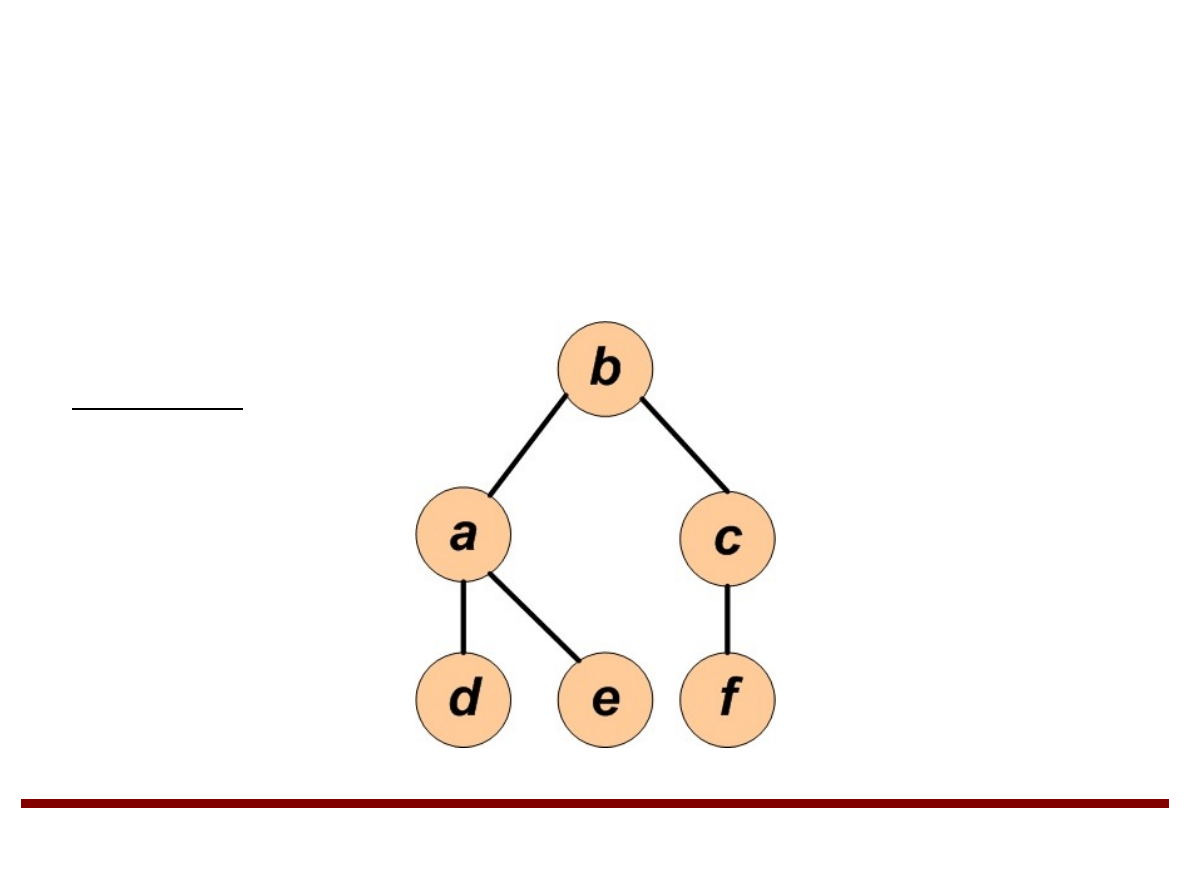
Drzewa (cd.)

Drzewo binarne jest drzewem z korzeniem, w którym

każdy wierzchołek ma co najwyżej dwa wierzchołki
potomne.

Przykład