ANALIZA WYNIKÓW POMIARÓW

(AWP)

Jednostka prowadz

ą

ca:

Instytut Metrologii i In

ż

ynierii Biomedycznej

Autor programu:

dr in

ż

. Jerzy Arendarski

Szacowanie niepewno

ś

ci pomiaru przy

wzorcowaniu przyrz

ą

dów pomiarowych

Wzorcowanie (inaczej kalibracja) to zbiór operacji ustalaj

ą

cych,

w okre

ś

lonych warunkach, relacj

ę

mi

ę

dzy warto

ś

ciami wielko

ś

ci

mierzonej wskazanymi przez przyrz

ą

d pomiarowy lub układ

pomiarowy albo warto

ś

ciami reprezentowanymi przez wzorzec miary

lub przez materiał odniesienia, a odpowiednimi warto

ś

ciami wielko

ś

ci

realizowanymi przez wzorce „jednostki miary”.

UWAGA!

Wynik wzorcowania pozwala na przypisanie wskazaniom

odpowiednich warto

ś

ci wielko

ś

ci mierzonej lub na wyznaczenie

poprawek wskaza

ń

.

Niepewno

ść

pomiaru przy wzorcowaniu

przyrz

ą

dów pomiarowych

Wzorcowania przyrz

ą

dów pomiarowych powinny

wykonywa

ć

laboratoria, które maj

ą

potwierdzone

kompetencje w tym zakresie.

To wymaganie spełniaj

ą

laboratoria akredytowane przez

Polskie Centrum Akredytacji (PCA).

Niepewno

ść

pomiaru przy wzorcowaniu

przyrz

ą

dów pomiarowych

Akredytowane laboratoria wzorcuj

ą

ce wystawiaj

ą ś

wiadectwa

wzorcowania przyrz

ą

dów pomiarowych.

Podstawowe wyniki zawarte w

ś

wiadectwach wzorcowania dotycz

ą

dokładno

ś

ci wskaza

ń

przyrz

ą

dów.

W

ś

wiadectwach wzorcowania, w zale

ż

no

ś

ci od rodzaju przyrz

ą

du

podawane s

ą

:

•poprawki wskaza

ń

•bł

ę

dy wskaza

ń

•warto

ś

ci poprawne wskaza

ń

Równanie pomiaru przy wzorcowaniu przyrz

ą

du powinno mie

ć

posta

ć

odpowiedni

ą

do wyznaczanego parametru.

Poprawka wskazania

to warto

ść

dodana algebraicznie do surowego

wyniku pomiaru w celu skompensowania bł

ę

du systematycznego (VIM).

Poprawk

ę

wskazania wyznacza si

ę

z zale

ż

no

ś

ci:

Formuła wyznaczania poprawki wskazania

W

-

N

-

P

w

=

∆

=

W

s

gdzie:

sW

∆

- bł

ą

d wskazania (systematyczny)

N

- warto

ść

odtwarzana przez wzorzec

W

-

ś

rednie wskazanie

Po uwzgl

ę

dnieniu warunków otoczenia i rozdzielczo

ś

ci przyrz

ą

du,

wzór na poprawk

ę

(równanie pomiaru) przyjmie ogóln

ą

posta

ć

:

wo

P

+

+

=

rw

w

P

W

-

N

P

Równanie pomiaru

przy wzorcowaniu przyrz

ą

du pomiarowego

gdzie:

- poprawka kompensuj

ą

ca bł

ą

d wskaza

ń

- poprawka na warunki

ś

rodowiskowe

rw

P

wo

P

Równanie pomiaru

przy wzorcowaniu przyrz

ą

du pomiarowego

Cz

ę

sto, szczególnie je

ś

li w

ś

wiadectwie wzorcowania potwierdzone jest,

ż

e bł

ę

dy wskaza

ń

przyrz

ą

du wzorcowanego nie przekraczaj

ą

bł

ę

dów granicznych

dopuszczalnych przyrz

ą

du ±E

g

(ang: maximum permissible errors – MPE),

w wyniku wzorcowania wyznacza si

ę

bł

ę

dy wskaza

ń

:

wo

rw

w

w

P

P

N

W

P

E

−

−

−

=

−

=

zatem:

wo

rw

w

N

W

E

∆

+

∆

+

−

=

gdzie:

rw

∆

wo

∆

- bł

ą

d rozdzielczo

ś

ci

- bł

ą

d spowodowany warunkami otoczenia

Równanie pomiaru

przy wzorcowaniu przyrz

ą

du pomiarowego

Z punktu widzenia analizy niepewno

ś

ci pomiaru, gdzie zakłada si

ę

,

ż

e warto

ś

ci oczekiwane bł

ę

dów i poprawek wyst

ę

puj

ą

cych w równaniach

pomiaru s

ą

zerowe, wła

ś

ciwym równie

ż

b

ę

dzie równanie:

wo

rw

w

P

P

N

W

E

+

+

−

=

Zatem równanie niepewno

ś

ci standardowej zło

ż

onej przyjmie posta

ć

:

)

(

)

(

)

(

)

(

2

2

4

2

2

3

2

2

2

2

2

1

wo

rw

P

u

c

P

u

c

N

u

c

w

u

c

+

+

+

=

=

E

u

)

u(P

w

w

)

(

Wyznaczanie niepewno

ś

ci standardowej zło

ż

onej

gdzie:

)

(W

u

)

( N

u

)

(

rw

P

u

)

(

wo

P

u

- niepewno

ść

standardowa zwi

ą

zana z rozrzutem wskaza

ń

- niepewno

ść

standardowa zwi

ą

zana z wzorcem

- niepewno

ść

standardowa zwi

ą

zana z ograniczon

ą

rozdzielczo

ś

ci

ą

przyrz

ą

du

- niepewno

ść

standardowa zwi

ą

zana z warunkami otoczenia

Tablica – współczynniki bezpiecze

ń

stwa dla odchylenia

standardowego s

x

z próbki (wg ENV ISO 14253-2:2001)

1

1,2

1,2

1,3

1,3

1,4

1,7

2,3

7,0

Współczynnik

Bezpiecze

ń

stwa,

h

10

9

8

7

6

5

4

3

2

Liczba pomiarów

w próbce,

n

Wyznaczanie niepewno

ś

ci standardowych składowych

Jak wyznaczy

ć

niepewno

ś

ci standardowe składowe (cz

ą

stkowe)?

?

)

(

=

W

u

- metoda typu A

1.

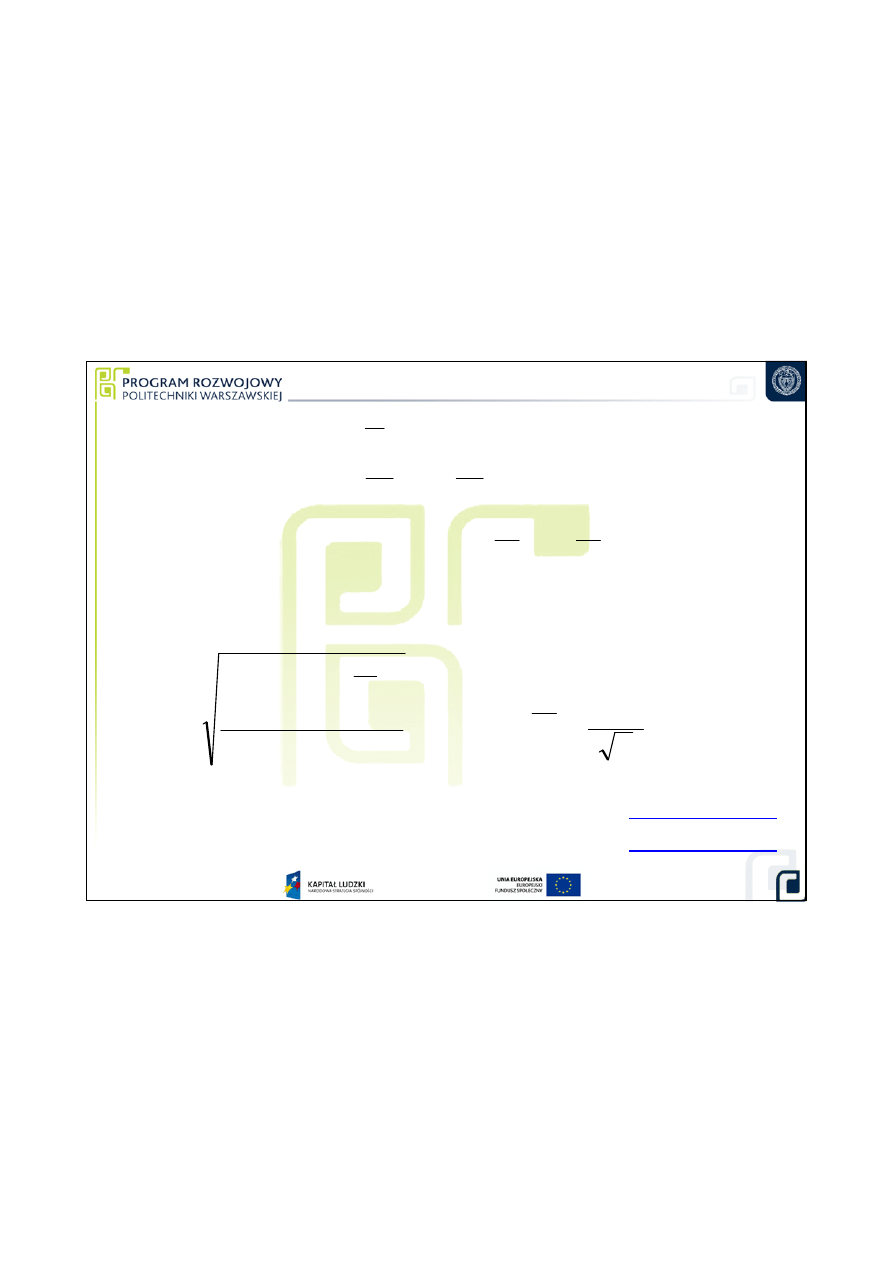
Niepewno

ść

standardowa dla małych próbek:

)

W

u(

h

)

W

s(

)

W

u(

⋅

=

Dla du

ż

ych próbek h =1, zatem

)

W

s(

)

W

u(

=

Metoda wyznaczania wariancji wspólnej:

)

1

(

)

2

−

−

=

∑∑

=

=

n

m

W

j

m

1

j

n

1

i

i

(W

s(W)

n

s(W)

)

W

u(

=

Przykład 8.1.a.doc

Przykład 8.2.a.doc

Niepewno

ść

zwi

ą

zana z rozrzutem wskaza

ń

Niepewno

ść

zwi

ą

zana z wzorcem

2.

?

)

(

=

N

u

Wzorce stosowane w procesach wzorcowania przyrz

ą

dów

pomiarowych musz

ą

mie

ć

aktualne

ś

wiadectwo wzorcowania.

W

ś

wiadectwach wzorcowania jest podana niepewno

ść

rozszerzona U(N) i współczynnik rozszerzenia k, odpowiadaj

ą

cy

poziomowi ufno

ś

ci około 95 %.

Zatem:

k

N

U

N

u

)

(

)

(

=

- metoda typu B

Je

ż

eli wzorcem jest stos płytek, niepewno

ść

standardow

ą

stosu nale

ż

y

policzy

ć

zgodnie z zasadami podanymi na poprzednim wykładzie.

Niepewno

ść

zwi

ą

zana z rozdzielczo

ś

ci

ą

przyrz

ą

du

3.

?

)

(

=

rw

P

u

Je

ż

eli rozdzielczo

ść

przyrz

ą

du wynosi d, to

3

2

)

(

d

P

u

rw

=

- metoda typu B

Dla przyrz

ą

dów analogicznych za rozdzielczo

ść

przyjmuje si

ę

najmniejsza warto

ść

odczytywan

ą

przy interpolacji działki elementarnej

Niepewno

ść

zwi

ą

zana z warunkami

ś

rodowiskowymi

4.

?

)

(

=

wo

P

u

W przypadku pomiarów wielko

ś

ci geometrycznych, je

ż

eli nie

wyst

ę

puj

ą

metody interferencyjne, spo

ś

ród wielko

ś

ci

wpływaj

ą

cych zwi

ą

zanych z warunkami otoczenia uwzgl

ę

dnia si

ę

temperatur

ę

.

Przy wzorcowaniu przyrz

ą

dów do bezpo

ś

rednich pomiarów

długo

ś

ci, korzysta si

ę

z uproszczonej formuły obliczania poprawki

temperaturowej.

Niepewno

ść

zwi

ą

zana z warunkami

ś

rodowiskowymi

t

L

P

P

t

wo

∆

∗

∗

=

=

α

gdzie:

L

α

t

∆

- długo

ść

wzorca

- u

ś

redniony współczynnik rozszerzalno

ś

ci cieplnej materiałów,

z których wykonane s

ą

wzorzec i przyrz

ą

d mierzony

- ró

ż

nica temperatur wzorcowanego przyrz

ą

du i zastosowanego wzorca

)

(

)

(

t

u

L

P

u

t

∆

∗

∗

=

α

5.

?

)

(

=

∆

t

u

C

t

t

°

±

=

∆

)

0

(

δ

3

)

(

t

t

u

δ

=

∆

- metoda typu B

Stos 1

Stos 2

Stos 3

Stos 4

Wysoko

ść

stosu

21,05

71,15

126,25

150,00

Wskazanie

1

21,06

71,15

126,27

150,01

2

21,06

71,16

126,26

150,02

3

21,05

71,16

126,26

150,02

4

21,05

71,15

126,26

150,02

5

21,04

71,15

126,27

150,02

Ś

rednie wskazanie

21,052

71,154

126,264

150,018

Bł

ą

d wskazania

0,002

0,004

0,014

0,018

Wyniki wzorcowania suwmiarki w zakresie pomiaru wymiarów zewn

ę

trznych:

Przykłady szacowania niepewno

ś

ci pomiaru przy wzorcowaniu

przyrz

ą

dów do bezpo

ś

rednich pomiarów długo

ś

ci

Przykład 1:
Wzorcowanie
suwmiarki elektronicznej
o zakresie pomiarowym (0 – 150)mm

Szacowanie niepewno

ś

ci pomiaru przy

wzorcowaniu suwmiarki

rw

n

wz

x

x

t

l

L

W

E

∆

+

∆

⋅

⋅

+

−

=

α

( )

( )

( )

( )

( )

( )

rw

wz

x

x

u

c

t

u

c

u

c

L

u

c

W

u

c

E

u

∆

+

∆

+

+

+

=

2

2

5

2

2

4

2

2

3

2

2

2

2

2

1

α

1. Równanie pomiaru

2. Równanie niepewno

ś

ci pomiaru

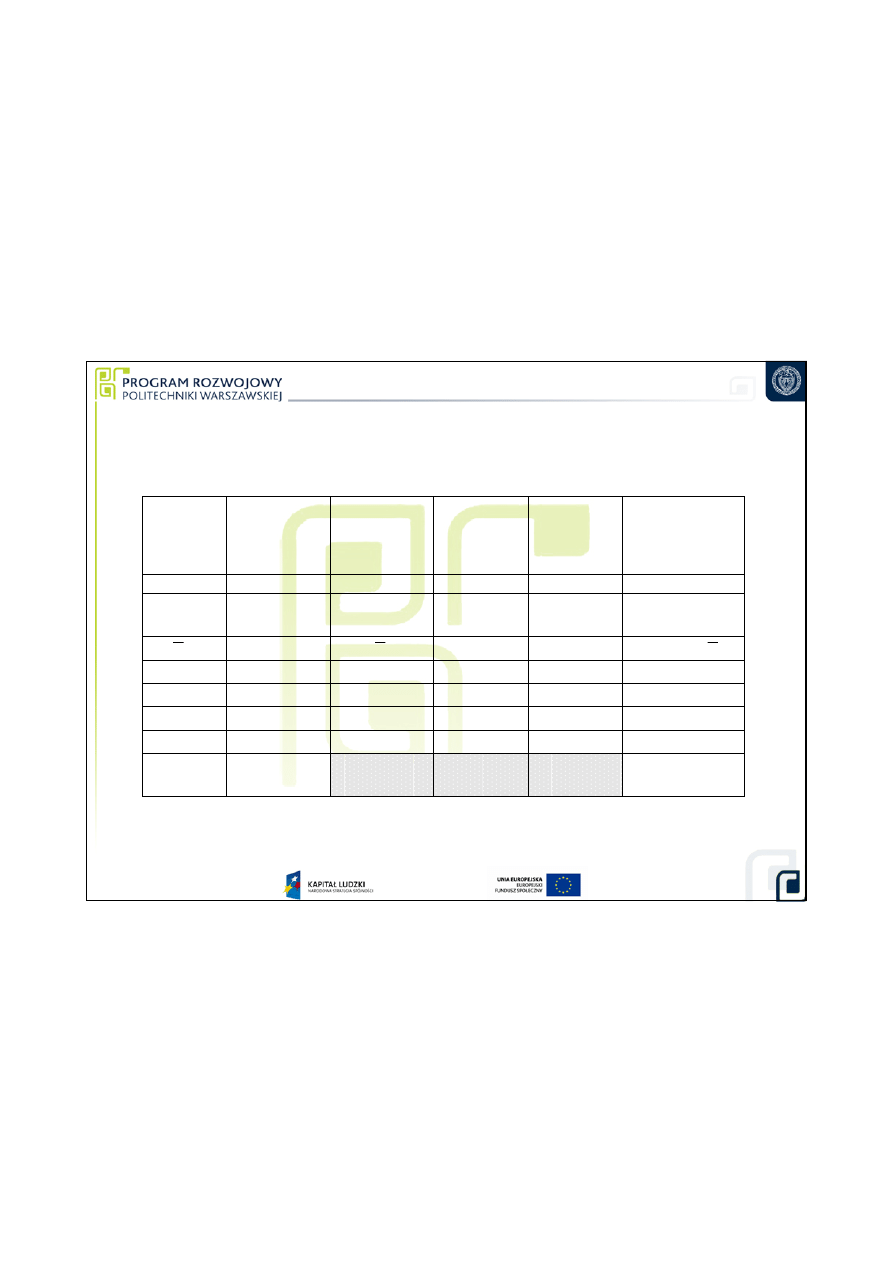
Symbol
wielkości

Estymata

wielkości

Niepewność

standardowa

Rozkład

prawdopodo-

bieństwa

Współczynnik

wpływu

Składowe

niepewności

standardowej

złożonej

1

2

3

4

5

6

X

i

x

ipop

a

i

c

i

u

i

(Y)

150,018

normalny

c

1

c

1·

L

wz

150,000

u(L

wz

)

trapezowy

c

2

c

2

·u(L

wz

)

α

11,5·10

-6

·ºC

-1

u(

α

)

trójkątny

c

3

c

3

·u(α)

∆

t

0ºC

u(

∆

t)

prostokątny

c

4

c

4

·u(

∆

t)

∆

rw

0

u(∆

rw

)

prostokątny

c

5

c

5

·u(∆

rw

)

E

x

0,018

u(E

x

)

x

W

)

(

x

W

u

)

(

x

W

u

3. Projekt bud

ż

etu niepewno

ś

ci pomiaru (pkt. pomiarowy nr 4)

Szacowanie niepewno

ś

ci pomiaru przy

wzorcowaniu suwmiarki

Szacowanie niepewno

ś

ci pomiaru przy

wzorcowaniu suwmiarki

1

1

=

∂

∂

=

x

x

W

E

c

0

3

=

∆

∗

=

∂

∂

=

t

l

E

c

n

x

α

1

2

−

=

∂

∂

=

wz

x

L

E

c

1

4

001725

,

0

−

°

⋅

=

∗

=

∆

∂

∂

=

C

mm

l

t

E

c

n

x

α

1

5

=

∆

∂

∂

=

rw

x

E

c

3.1. Obliczenie wspó

ł

czynników wp

ł

ywu

3.2. Niepewno

ś

ci standardowe sk

ł

adowe

3.2.1 Niepewno

ść

standardowa zwi

ą

zana z rozrzutem wskaza

ń

wzorcowanej suwmiarki

( )

(

)

00613

,

0

=

−

=

∑∑

=

=

16

W

W

W

s

2

j

i

4

1

j

5

1

i

0,00274

5

≈

≈

)

(

)

(

W

s

W

u

Szacowanie niepewno

ś

ci pomiaru przy

wzorcowaniu suwmiarki

C

155

,

C

2

)

(

°

≈

°

=

∆

1

3

t

u

0029

,

0

2

01

,

0

)

(

≈

=

∆

3

rw

u

3.2.3 Niepewno

ść

standardowa zwi

ą

zana z ró

ż

nic

ą

temperatur

Przyj

ę

to:

∆

t = (0

±

2)ºC

Zatem:

3.2.4 Niepewno

ść

standardowa zwi

ą

zana z rozdzielczo

ś

ci

ą

3.2.2 Niepewno

ść

standardowa zwi

ą

zana z wzorcem

Wykorzystano p

ł

ytki wzorcowe klasy 2 bez uwzgl

ę

dnienia poprawek

00083

,

0

3

8

,

0

2

,

1

)

(

2

2

2

50

2

100

=

+

=

+

=

3

3

e

e

wz

t

t

L

u

Symbol
wielkości

Estymata

wielkości

Niepewność

standardowa

Rozkład

prawdopodo-

bieństwa

Współczynnik

wpływu

Składowe

niepewności

standardowej

złożonej

1

2

3

4

5

6

X

i

x

ipop

a

i

c

i

u

i

(Y)

150,018

0,00274

normalny

1

0,00274

L

wz

150,000

0,00083

trapezowy

-1

-0,00083

α

11,5·10

-6

·ºC

-1

-

trójkątny

0

0

∆

t

0ºC

1,155ºC

prostokątny

0,001725 []

0,00199

∆

rw

0

0,0029

prostokątny

1

0,0029

E

x

0,018

0,004535

4. Bud

ż

et niepewno

ś

ci pomiaru (pkt. pomiarowy nr 4)

x

W

5. Niepewno

ść

pomiaru przy wzorcowaniu suwmiarki

U(E

150

) = 2·0,004535 mm= 0,00907 mm = 0,009 mm

6. Wynik wzorcowania

E

150

= (0,018

±

0,009) mm

Szacowanie niepewno

ś

ci pomiaru przy

wzorcowaniu suwmiarki

Punkt pomiarowy

u(L

wz

) u(

∆

t) u(∆

rw

) u(e

s

) U(e

s

)

µ

m

21,05

2,74

0,43

1,15

2,90

4,01

8,0

71,15

2,74

0,63

1,15

2,90

4,14

8,3

126,25

2,74

0,82

1,15

2,90

4,42

8,8

150,00

2,74

0,83

1,15

2,90

4,53

9,1

6. Syntetyczny bud

ż

et niepewno

ś

ci pomiaru przy wzorcowaniu suwmiarki

)

(

x

W

u

W

ś

wiadectwie wzorcowania mo

ż

e by

ć

podana jedna niepewno

ść

pomiaru dla

wszystkich punktów pomiarowych:

U(E

w

) = 0,009 mm

Szacowanie niepewno

ś

ci pomiaru przy

wzorcowaniu suwmiarki

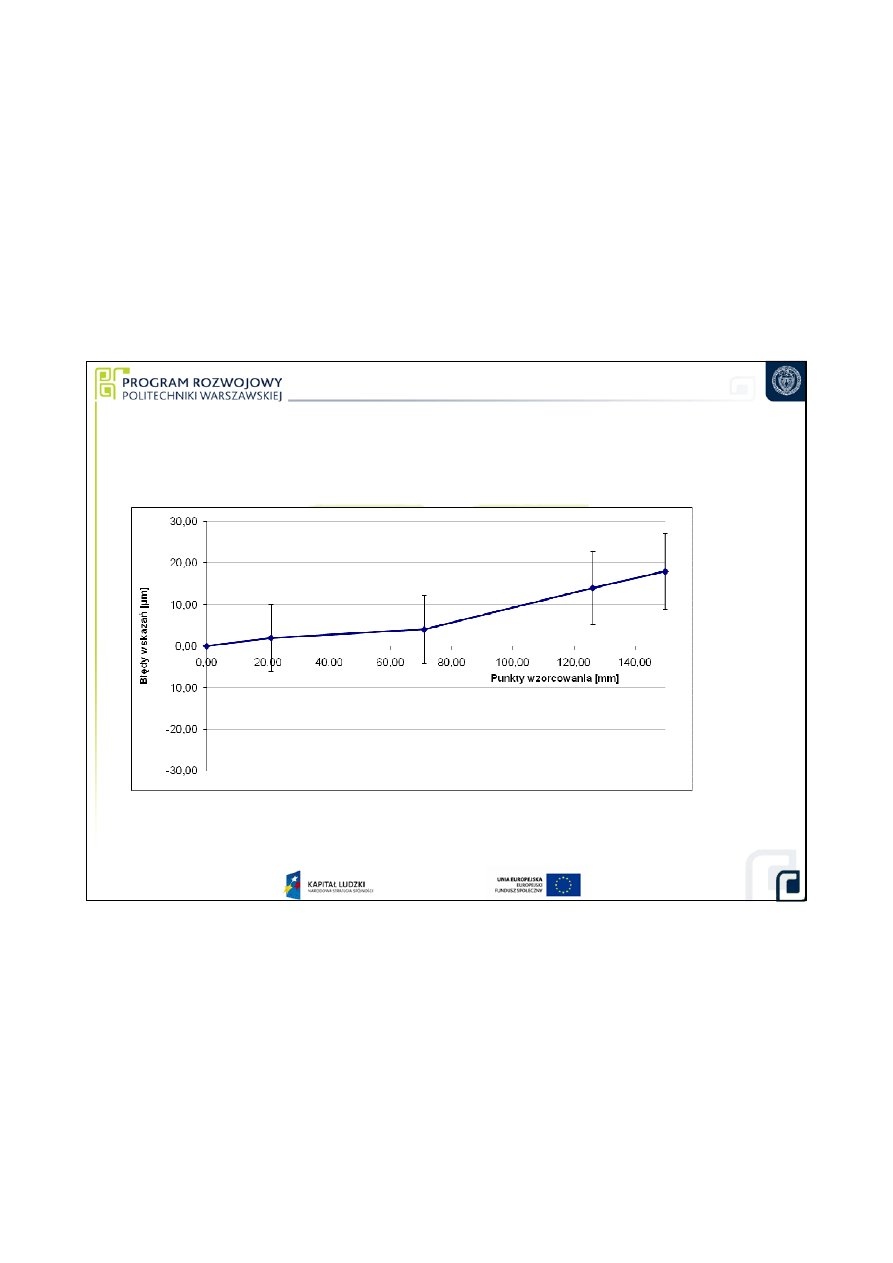
7. Graficzne przedstawienie wyników wzorcowania suwmiarki

Szacowanie niepewno

ś

ci pomiaru przy

wzorcowaniu suwmiarki

Przykłady szacowania niepewno

ś

ci pomiaru przy wzorcowaniu

przyrz

ą

dów do bezpo

ś

rednich pomiarów długo

ś

ci

Przykład 2:
Wzorcowanie
mikrometru elektronicznego
o zakresie pomiarowym (0 – 25)mm
i rozdzielczo

ś

ci d = 0,001 mm

Punkt

pomiarowy

mm

Wyniki pomiarów

mm

B

łą

d

wskazania

µm

1

2

3

4

5

0

0

0,001

0

0

0

0,2

5,12

5,12

5,121

5,12

5,121

5,121

0,6

10,25

10,249

10,25

10,25

10,249

10,249

-0,6

15,37

15,368

15,368

15,369

15,368

15,368

-1,8

21,5

21,502

21,501

21,502

21,501

21,501

1,4

25

25,003

25,003

25,002

25,003

25,003

2,8

Wyniki wzorcowania mikrometru:

Szacowanie niepewno

ś

ci pomiaru przy

wzorcowaniu mikrometru

rw

n

wz

x

x

t

l

L

W

E

∆

+

∆

⋅

⋅

+

−

=

α

( )

( )

( )

( )

( )

( )

rw

wz

x

x

u

c

t

u

c

u

c

L

u

c

W

u

c

E

u

∆

+

∆

+

+

+

=

2

2

5

2

2

4

2

2

3

2

2

2

2

2

1

α

1. Równanie pomiaru

2. Równanie niepewno

ś

ci pomiaru

Szacowanie niepewno

ś

ci pomiaru przy

wzorcowaniu mikrometru

Symbol
wielkości

Estymata

wielkości

Niepewność

standardowa

Rozkład

prawdopodo

-bieństwa

Współczynni

k

wpływu

Składowe

niepewności

standardowej

złożonej

1

2

3

4

5

6

X

i

x

ipop

a

i

c

i

u

i

(Y)

21,5014

normalny

c

1

L

wz

21,500

u(L

wz

)

trapezowy

c

2

c

2

·u(L

wz

)

α

11,5·10

-

6

·ºC

-1

u(

α

)

trójkątny

c

3

c

3

·u(α)

∆

t

0ºC

u(

∆

t)

prostokątny

c

4

c

4

·u(

∆

t)

∆

rw

0

u(∆

rw

)

prostokątny

c

5

c

5

·u(∆

rw

)

E

x

0,0014

u(E

x

)

x

W

)

(

1

x

W

u

c

∗

)

(

x

W

u

3. Projekt bud

ż

etu niepewno

ś

ci pomiaru (pkt. pomiarowy nr 5)

1

1

=

∂

∂

=

x

x

W

E

c

0

3

=

∆

∗

=

∂

∂

=

t

l

E

c

n

x

α

1

2

−

=

∂

∂

=

wz

x

L

E

c

1

4

000247

,

0

−

°

⋅

=

∗

=

∆

∂

∂

=

C

mm

l

t

E

c

n

x

α

1

5

=

∆

∂

∂

=

rw

x

E

c

( )

(

)

00051

,

0

=

−

=

∑∑

=

=

24

W

W

W

s

2

j

i

4

1

j

5

1

i

0,00023

5

≈

≈

)

(

)

(

W

s

W

u

3.1. Obliczenie wspó

ł

czynników wp

ł

ywu

3.2. Niepewno

ś

ci standardowe sk

ł

adowe

3.2.1 Niepewno

ść

standardowa zwi

ą

zana z rozrzutem wskaza

ń

wzorcowanego mikrometru

Szacowanie niepewno

ś

ci pomiaru przy

wzorcowaniu mikrometru

00021

,

0

3

2

,

0

3

,

0

)

(

2

2

2

5

,

1

2

20

=

+

=

+

=

3

3

e

e

wz

t

t

L

u

C

155

,

C

2

)

(

°

≈

°

=

∆

1

3

t

u

00029

,

0

2

001

,

0

)

(

≈

=

∆

3

rw

u

3.2.2 Niepewno

ść

standardowa zwi

ą

zana z wzorcem

Wykorzystano p

ł

ytki wzorcowe klasy 1, bez uwzgl

ę

dnienia poprawek

3.2.3 Niepewno

ść

standardowa zwi

ą

zana z ró

ż

nic

ą

temperatur

Przyj

ę

to:

∆

t = (0

±

2)ºc

Zatem:

3.2.4 Niepewno

ść

standardowa zwi

ą

zana z rozdzielczo

ś

ci

ą

Szacowanie niepewno

ś

ci pomiaru przy

wzorcowaniu mikrometru

Symbol
wielkości

Estymata wielkości

Niepewność

standardowa

Rozkład

prawdopodo-

bieństwa

Współczynnik

wpływu

Składowe niepewności
standardowej złożonej

1

2

3

4

5

6

X

i

x

ipop

a

i

c

i

u

i

(Y)

21,5014

0,00023

normalny

1

0,00023

L

wz

21,500

0,00021

trapezowy

-1

-0,00021

α

11,5·10

-6

·ºC

-1

-

trójkątny

0

0

∆

t

0ºC

1,155ºC

prostokątny

0,000247 []

0,00029

∆

rw

0

0,00029

prostokątny

1

0,00029

E

x

0,0014

0,0005149

4. Bud

ż

et niepewno

ś

ci pomiaru (pkt. pomiarowy nr 5)

x

W

5. Niepewno

ść

pomiaru przy wzorcowaniu mikrometru

U(E

21,5

) = 2·0,0005149 mm= 0,00103 mm = 0,0010 mm

6. Wynik wzorcowania

E

21,5

= (0,0014

±

0,0010) mm

Szacowanie niepewno

ś

ci pomiaru przy

wzorcowaniu mikrometru

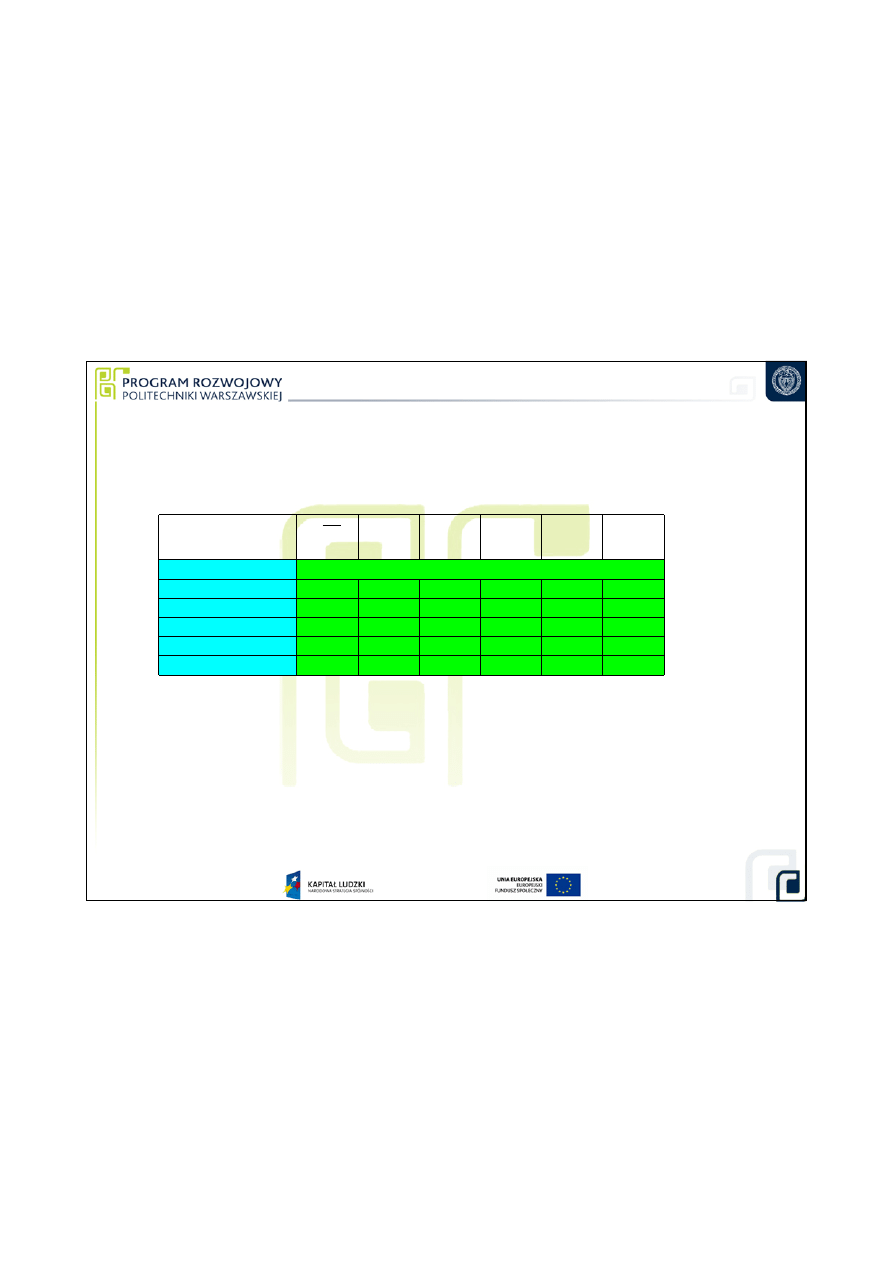
Punkt pomiarowy

u(L

wz

) u(

∆

t) u(∆

rw

) u(e

s

) U(e

s

)

µ

m

5,12

0,23

0,2

1,15

0,29

0,405

0,81

10,25

0,23

0,2

1,15

0,29

0,43

0,86

15,37

0,23

0,24

1,15

0,29

0,47

0,94

21,5

0,23

0,21

1,15

0,29

0,515

1,03

25

0,23

0,17

1,15

0,29

0,53

1,06

6. Syntetyczny bud

ż

et niepewno

ś

ci pomiaru przy wzorcowaniu mikrometru

)

(

x

W

u

W

ś

wiadectwie wzorcowania mo

ż

e by

ć

podana jedna niepewno

ść

pomiaru

dla wszystkich punktów pomiarowych:

U(E

w

) = 0,0011 mm

Szacowanie niepewno

ś

ci pomiaru przy

wzorcowaniu mikrometru

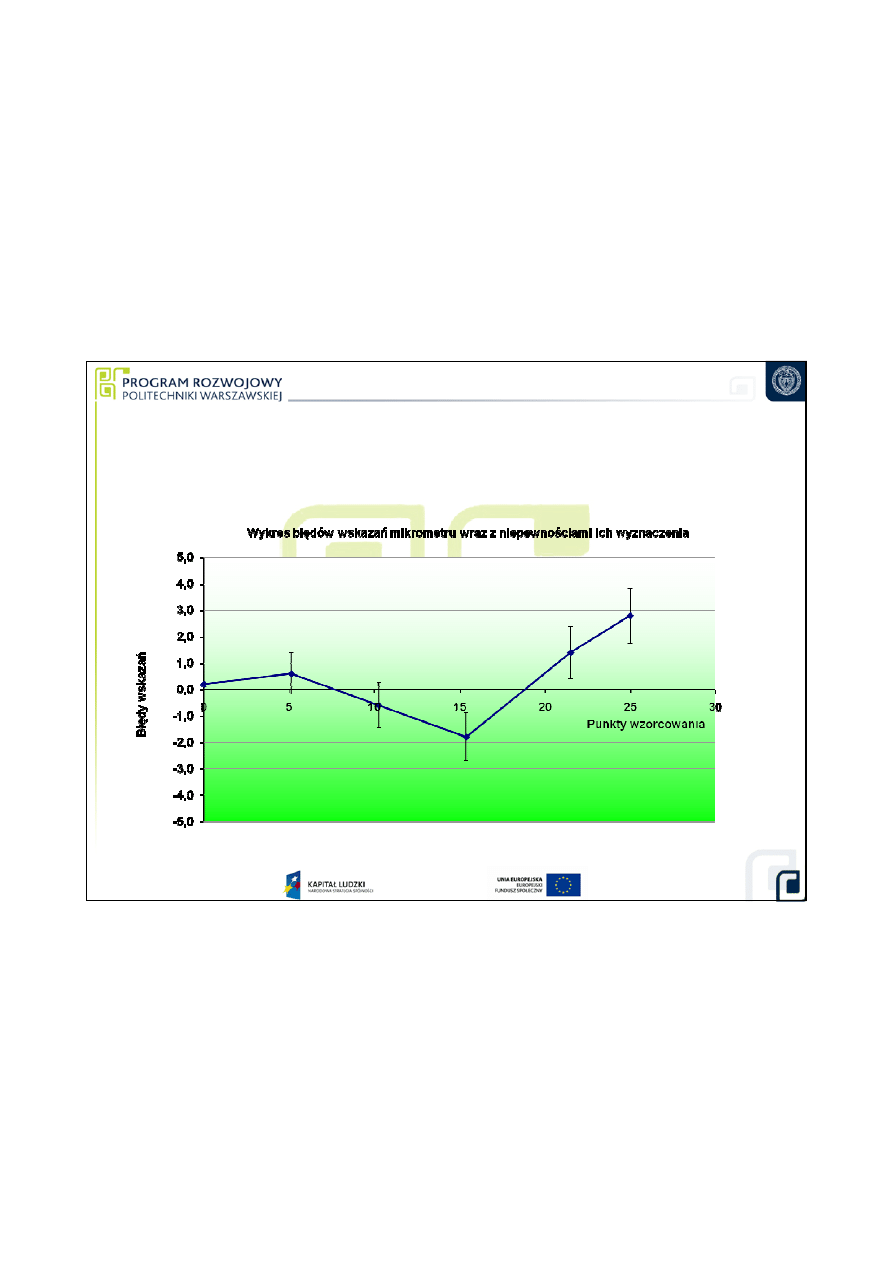
7. Graficzne przedstawienie wyników wzorcowania mikrometru

Szacowanie niepewno

ś

ci pomiaru przy

wzorcowaniu mikrometru

Niepewno

ść

pomiaru przy wzorcowaniu

ś

rednicówki czujnikowej

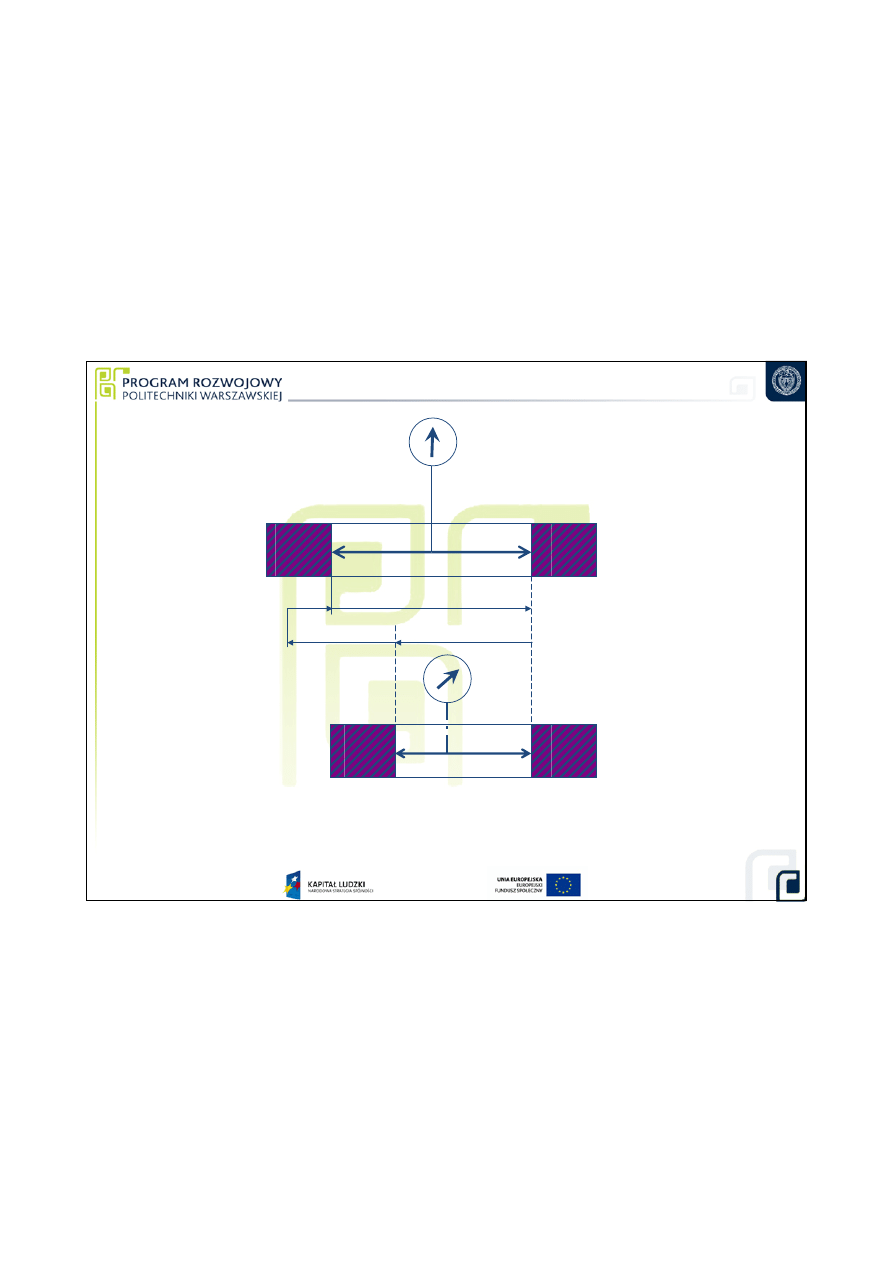
W

1

W

2

L

2

L

1

W

1

–W

2

L

2

L

1

Ex

(

)

1

1

2

2

1

2

1

2

1

2

1

2

t

l

t

l

L

L

W

W

E

n

n

rw

rw

x

∆

⋅

⋅

−

∆

⋅

⋅

+

−

+

−

+

−

=

α

α

δ

δ

Niepewno

ść

pomiaru przy wzorcowaniu

ś

rednicówki czujnikowej

Niepewno

ść

pomiaru przy wzorcowaniu

ś

rednicówki czujnikowej

1

1

2

2

1

2

1

2

1

2

1

2

)

(

t

l

t

l

L

L

W

W

E

n

n

rw

rw

wz

wz

x

∆

⋅

⋅

−

∆

⋅

⋅

+

∆

−

∆

+

−

+

−

=

α

α

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

1

2

2

10

1

2

2

9

2

2

2

8

2

2

2

7

2

2

6

2

2

5

1

2

2

4

2

2

2

3

1

2

2

2

2

2

2

1

1

2

t

u

c

u

c

t

u

c

u

c

u

c

u

c

L

u

c

L

u

c

W

u

c

W

u

c

E

u

rw

rw

wz

wz

x

∆

+

+

∆

+

+

∆

+

∆

+

+

+

+

=

α

α

2. Równanie niepewno

ś

ci pomiaru

1. Równanie pomiaru

Symbol
wielkości

Estymata wielkości

Niepewność

standardowa

Rozkład

prawdopodo-

bieństwa

Współczynnik

wpływu

Składowe

niepewności

standardowej

złożonej

1

2

3

4

6

7

X

i

x

ipop

a

i

c

i

u

i

(Y)

normalny

c

1

normalny

c

2

L

wz2

l

wz2

u

(

l

wz2

)

normalny

c

3

c

3

⋅

u

(

l

wz2

)

L

wz1

l

wz1

u

(

l

wz1

)

normalny

c

4

c

4

⋅

u

(

l

wz1

)

∆

rw2

δ

rw2

u

(

δ

rw2

)

prostokątny

c

5

c

5

⋅

u(

δ

rw2

)

∆

rw1

δ

rw1

u

(

δ

rw1

)

prostokątny

c

6

c

6

⋅

u(

δ

rw1

)

α

2

11,5·10

-6

·ºC

-1

u

(

α

2

)

trójkątny

c

7

c

7

⋅

u

(

α

2

)

∆

t

2

0

u

(

δ

t

2

)

prostokątny

c

8

c

8

⋅

u

(

δ

t

2

)

α

1

11,5·10

-6

·ºC

-1

u

(

α

1

)

trójkątny

c

9

c

9

⋅

u

(

α

1

)

∆

t

1

0

u

(

δ

t

1

)

prostokątny

c

10

c

10

⋅

u

(

δ

t

2

)

Ex

ex

u(Ex)

2

W

2

w

)

(

2

w

u

)

(

2

w

u

c

1

⋅

1

W

1

w

)

(

1

w

u

)

(

1

w

u

c

2

⋅

3. Projekt bud

ż

etu niepewno

ś

ci pomiaru

Niepewno

ść

pomiaru przy wzorcowaniu

ś

rednicówki czujnikowej

1

1

2

2

1

2

1

2

1

2

1

2

)

(

t

l

t

l

L

L

W

W

E

n

n

rw

rw

wz

wz

x

∆

⋅

⋅

−

∆

⋅

⋅

+

∆

−

∆

+

−

+

−

=

α

α

1

2

1

=

∂

∂

=

W

E

c

x

1

1

2

−

=

∂

∂

=

W

E

c

x

1

2

3

=

∂

∂

=

wz

x

L

E

c

1

1

4

−

=

∂

∂

=

wz

x

L

E

c

1

2

5

=

∆

∂

∂

=

rw

x

E

c

1

1

6

−

=

∆

∂

∂

=

rw

x

E

c

0

2

2

7

2

=

∆

∗

=

∂

∂

=

t

l

E

c

n

x

α

1

2

2

8

C

mm

001725

,

0

2

−

°

⋅

=

∗

=

∆

∂

∂

=

α

n

x

l

t

E

c

0

1

1

9

1

=

∆

∗

−

=

∂

∂

=

t

l

E

c

n

x

α

1

1

1

10

C

mm

001751

,

0

1

−

°

⋅

−

=

∗

−

=

∆

∂

∂

=

α

n

x

l

t

E

c

3.1. Wspó

ł

czynniki wp

ł

ywu

Niepewno

ść

pomiaru przy wzorcowaniu

ś

rednicówki czujnikowej

( )

(

)

mm

0011

,

0

=

−

=

∑∑

=

=

27

W

W

W

s

2

j

i

3

1

j

10

1

i

0,00078mm

2

≈

≈

)

(

)

(

W

s

W

u

3.2. Niepewno

ś

ci standardowe sk

ł

adowe

3.2.1 Niepewno

ść

standardowa zwi

ą

zana z rozrzutem wskaza

ń

wzorcowanej

ś

rednicówki

Zakres rozrzutu wskaza

ń ś

rednicówki czujnikowej wyznacza si

ę

na podstawie trzech

dziesi

ę

cioelementowych serii pomiarów wykonanych w trzech odpowiednio dobranych punktach

zakresu pomiarowego. Dla trzech serii po n = 10 pomiarów, otrzymano:

3.2.2 Niepewno

ś

ci standardowe zwi

ą

zane z wzorcami

Do wzorcowania średnic

ó

wki zastosowano wzorce pierścieniowe. W świadectwie

wzorcowania kompletu pierścieni, dla wykorzystanych w przykładzie pierścieni podano:

U(L

wz1

) = U(L

wz2

) = 0,0011 mm

Zatem

u(Lwz1) = u(Lwz2) = 0,00055 mm

Niepewno

ść

pomiaru przy wzorcowaniu

ś

rednicówki czujnikowej

mm

mm

u

u

u

rw

rw

rw

00029

,

0

2

001

,

0

)

(

)

(

)

(

2

1

≈

=

∆

=

∆

=

∆

3

1

6

1

6

2

1

10

82

,

0

10

2

)

(

)

(

)

(

−

−

−

−

°

⋅

≈

°

⋅

=

=

=

C

C

u

u

u

6

α

α

α

3.2.3 Niepewno

ść

standardowa zwi

ą

zana z rozdzielczo

ś

ci

ą ś

rednicówki

Ś

rednicówka jest wyposa

ż

ona w czujnik elektroniczny o rozdzielczo

ś

ci 0,001 mm, wi

ę

c

3.2.4 Niepewno

ś

ci standardowe zwi

ą

zane ze wspó

ł

czynnikami rozszerzalno

ś

ci

cieplnej materia

ł

ów, z których wykonane s

ą

wzorce i

ś

rednicówka

Przyj

ę

to,

ż

e wspó

ł

czynniki rozszerzalno

ś

ci materia

ł

ów spe

ł

niaj

ą

wymaganie:

α

= (11,5

±

2,0)

⋅

10

-6

°

C

-1.

Zak

ł

adaj

ą

c rozk

ł

ad Simpsona, otrzymuje si

ę

:

Niepewno

ść

pomiaru przy wzorcowaniu

ś

rednicówki czujnikowej

C

C

t

u

t

u

t

u

°

≈

°

=

∆

=

∆

=

∆

577

,

0

1

)

(

)

(

)

(

2

1

3

3.2.5 Niepewno

ś

ci standardowe zwi

ą

zane z ró

ż

nicami temperatur

ś

rednicówki i wzorców

Na podstawie bada

ń

przyj

ę

to,

ż

e ró

ż

nica temperatur mi

ę

dzy przyrz

ą

dem

i wzorcem nie przekracza

∆

t = (0

±

1)

°

C

-1

Zatem:

Niepewno

ść

pomiaru przy wzorcowaniu

ś

rednicówki czujnikowej

Symbol
wielkości

Estymata

wielkości

Niepewność

standardowa

Rozkład

prawdopodo-

bieństwa

Współczynnik

wpływu

Składowe

niepewności

standardowej

złożonej

1

2

3

4

6

7

X

i

x

ipop

a

i

c

i

u

i

(Y)

2,305

0,00078

normalny

1

0,00078

0,000

0,00078

normalny

-1

-0,00078

L

wz2

150

0,00055

normalny

1

0,00055

L

wz1

152,3

0,00055

normalny

-1

-0,00055

∆

rw2

0

0,00029

prostokątny

1

0,00029

∆

rw1

0

0,00029

prostokątny

-1

-0,00029

α

2

11,5·10

-6

·ºC

-1

0,82·10

-6

·ºC

-1

trójkątny

0

0

∆

t

2

0

0,577

°

C

prostokątny 0,001725 []

0,000995

α

1

11,5·10

-6

·ºC

-1

0,82·10

-6

·ºC

-1

trójkątny

0

0

∆

t

1

0

0,577

°

C

prostokątny -0,001751 []

0,00101

E

x

0,005

0,00200

2

W

1

W

4. Bud

ż

et niepewno

ś

ci pomiaru

(wzorcowanie

ś

rednicówki czujnikowej w wybranym punkcie pomiarowym)

U(E

x

) = 2·0,00200 mm = 0,004 mm

6. Wynik wzorcowania

E

x

= (0,005

±

0,004) mm

Niepewno

ść

pomiaru przy wzorcowaniu

ś

rednicówki czujnikowej

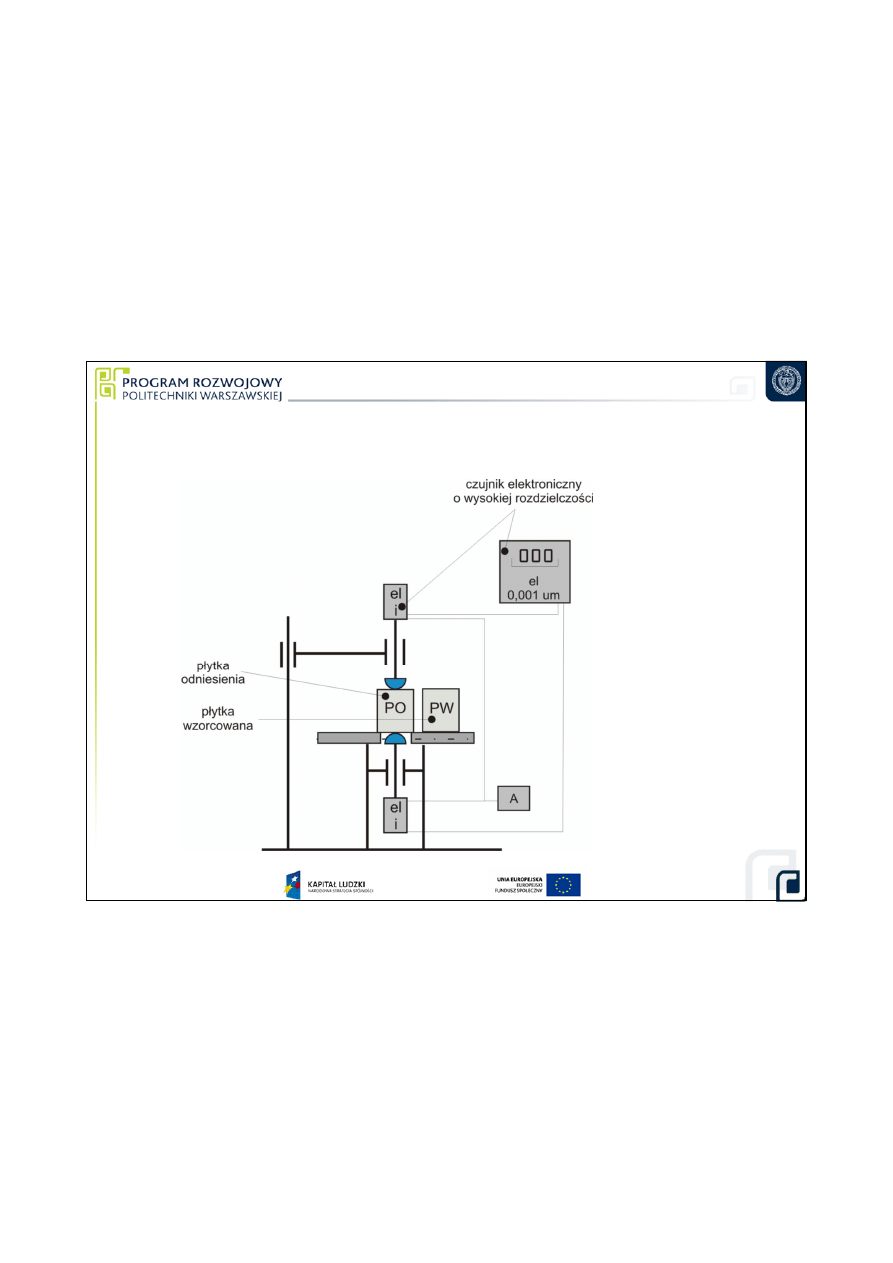
Schemat pomiaru d

ł

ugo

ś

ci p

ł

ytki metod

ą

porównawcz

ą

Wyznaczanie poprawek dla wzorców porównywanych

z wzorcami odniesienia za pomoc

ą

komparatorów

B

Σ

+

+

+

−

+

=

P

E

P

W

P

W

E

wzo

w

w

wz

)

(

)

(

1

1

2

2

2

W

2

w

P

1

W

2

w

P

wzo

E

Σ

P

Σ

+

+

−

+

=

P

E

W

P

W

E

wzo

w

wz

1

2

2

)

(

gdzie:

-

ś

rednie wskazanie komparatora na wzorcu mierzonym,

- poprawka wskazania komparatora na wzorcu mierzonym,

-

ś

rednie wskazanie komparatora na wzorcu odniesienia,

- poprawka wskazania komparatora na wzorcu odniesienia,

- b

łą

d wzorca odniesienia,

- suma poprawek (poprawki na warunki

ś

rodowiskowe, wpływ nacisku

pomiarowego i inne) – tu potraktowana jako wcze

ś

niej obliczona składowa

.

Je

ż

eli komparator jest zerowany na wzorcu odniesienia, to:

1. Równanie pomiaru

Wyznaczanie poprawek dla wzorców porównywanych

z wzorcami odniesienia za pomoc

ą

komparatorów

( )

( )

( )

( )

( )

( )

Σ

+

+

+

+

=

P

u

c

E

u

c

W

u

c

P

u

c

W

u

c

E

u

wzo

w

wz

2

2

5

2

2

4

1

2

2

3

2

2

2

2

2

2

2

1

2. Równanie niepewno

ś

ci pomiaru

Symbol
wielkości

Estymata

wielkości

Niepewność

standardowa

Rozkład

prawdopodo

-bieństwa

Współczynni

k

wpływu

Składowe

niepewności

standardowej

złożonej

1

2

3

4

5

6

X

i

x

ipop

a

i

c

i

u

i

(Y)

normalny

c

1

c

1·

P

w2

p

w2

u(P

w2

)

prostokątny

c

2

c

2

·u(P

w2

)

normalny

c

3

c

3·

E

wzo

e

wzo

u(E

wzo

)

normalny

c

4

c

4

·u(E

wzo

)

P

Σ

p

Σ

u(P

Σ

)

normalny

c

5

c

5

·u(P

Σ

)

E

x

e

x

u(E

x

)

2

W

2

w

)

(

2

W

u

)

(

2

W

u

1

W

1

w

)

(

1

W

u

)

(

1

W

u

3. Projekt bud

ż

etu niepewno

ś

ci pomiaru

Wyznaczanie poprawek dla wzorców porównywanych

z wzorcami odniesienia za pomoc

ą

komparatorów

1

2

1

=

∂

∂

=

W

E

c

x

1

1

3

−

=

∂

∂

=

W

E

c

x

1

2

2

+

=

∂

∂

=

w

x

P

E

c

1

4

=

∂

∂

=

wzo

x

E

E

c

1

5

=

∂

∂

=

Σ

P

E

c

x

( )

(

)

1

-

n

W

W

(W)

u

W

s

2

i

n

1

i

p

−

=

=

∑

=

1

n

)

(

)

(

)

(

)

(

1

2

W

s

W

u

W

u

W

u

≈

=

=

3.1. Obliczenie wspó

ł

czynników wp

ł

ywu

3.2. Niepewno

ś

ci standardowe sk

ł

adowe

3.2.1 Niepewno

ść

standardowa zwi

ą

zana z rozrzutem wskaza

ń

komparatora

Laboratorium mo

ż

e okresowo wyznacza

ć

odchylenie standardowe eksperymentalne wskaza

ń

komparatora na podstawie d

ł

ugiej serii pomiarów:

a nast

ę

pnie, znaj

ą

c odchylenie standardowe rozrzutu wskaza

ń

, wyznacza

ć

:

Wyznaczanie poprawek dla wzorców porównywanych

z wzorcami odniesienia za pomoc

ą

komparatorów

4

3

2

2

2

)

(

wzk

k

w

U

E

P

u

+

=

3

2

2

)

(

)

(

wzk

k

w

U

E

P

u

+

=

2

)

(

)

(

wzo

wzo

E

U

E

u

=

2

)

(

)

(

Σ

Σ

=

P

U

P

u

3.2.2 Niepewno

ść

standardowa zwi

ą

zana z b

łę

dami wskaza

ń

komparatora

lub

3.2.3 Niepewno

ść

standardowa zwi

ą

zana z wzorcem odniesienia

3.2.4 Niepewno

ść

standardowa zwi

ą

zana z poprawk

ą

sumaryczn

ą

Przyk

ł

ady b

ę

d

ą

omówione w ramach przedmiotu

„Atestacja aparatury pomiarowej”

Wyznaczanie poprawek dla wzorców porównywanych

z wzorcami odniesienia za pomoc

ą

komparatorów

„Zaleca si

ę

, aby b

łą

d wynikaj

ą

cy z wzorcowania by

ł

mo

ż

liwie jak najmniejszy. W

wi

ę

kszo

ś

ci dziedzin

pomiarowych nie powinien on przekracza

ć

jednej

trzeciej,

a

najlepiej

jednej

dziesi

ą

tej

b

łę

du

dopuszczalnego

wyposa

ż

enia

potwierdzonego

podczas jego u

ż

ytkowania”

PN-ISO 10012 - 1

Dzi

ę

kuj

ę

za uwag

ę

i zapraszam na dalsz

ą

cz

ęść

wykładu

Szacowanie niepewno

ś

ci pomiaru przy

wzorcowaniu przyrz

ą

dów pomiarowych