ANALIZA WYNIKÓW POMIARÓW

(AWP)

Jednostka prowadz

ą

ca:

Instytut Metrologii i In

ż

ynierii Biomedycznej

Autor programu:

dr in

ż

. Jerzy Arendarski

Procedura ogólna szacowania

niepewno

ś

ci pomiaru

2010-10-08

Obliczanie niepewno

ś

ci nie jest ani zadaniem rutynowym, ani zadaniem

czysto matematycznym; zale

ż

y ono od szczegółowej wiedzy o naturze

wielko

ś

ci mierzonej i pomiaru. Dlatego te

ż

jako

ść

i u

ż

yteczno

ść

niepewno

ś

ci podawanej z wynikiem pomiaru w zasadniczy sposób zale

ż

y

od zrozumienia, krytycznej analizy i rzetelno

ś

ci tych, którzy uczestnicz

ą

w

ocenie jej warto

ś

ci. (Przewodnik ISO pkt.3.4.8)

Procedura ogólna szacowania niepewno

ś

ci pomiaru

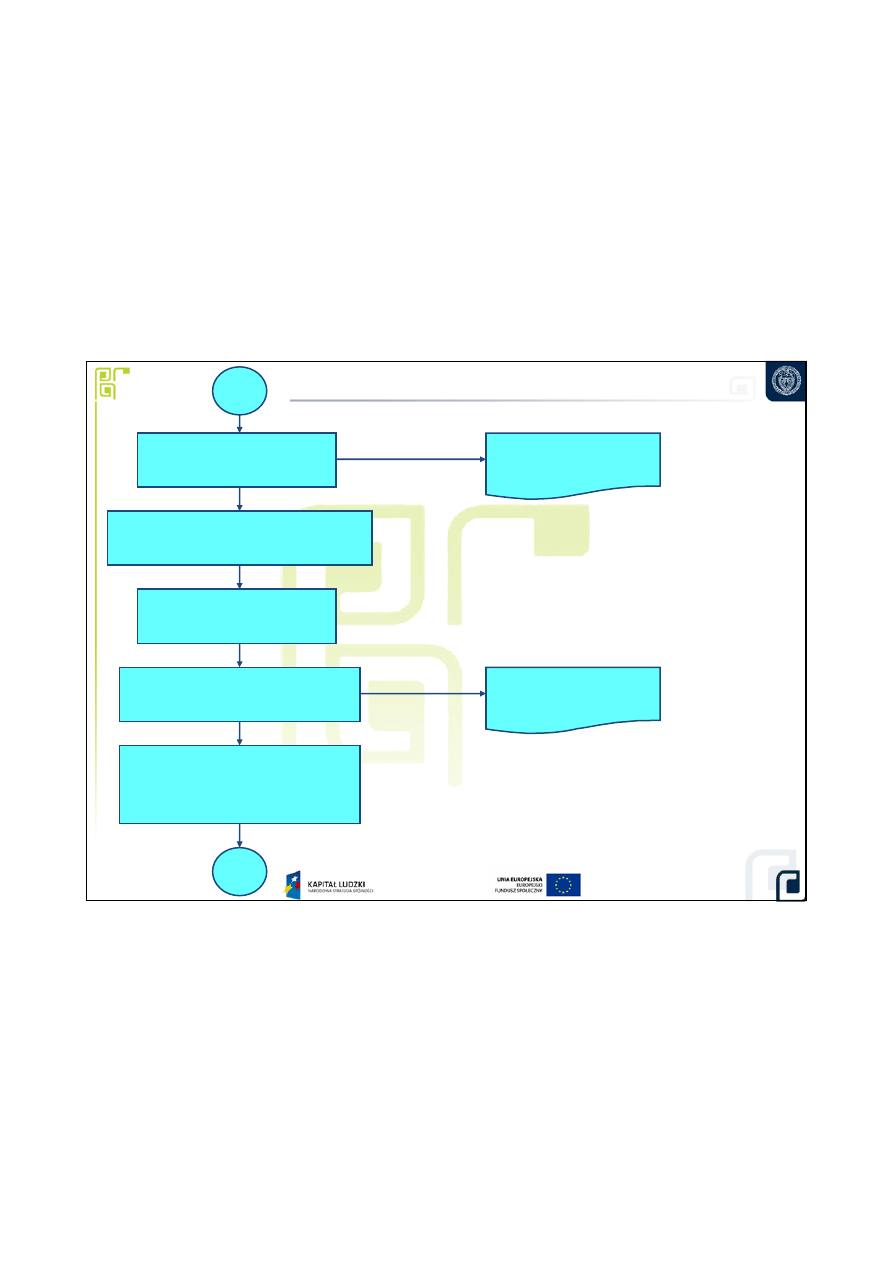
2. Okre

ś

lenie dopuszczalnej

niepewno

ś

ci pomiaru (Udop)

3. Analiza metod

pomiarowych

5. Sformułowanie

równania pomiaru

Y=f(X1, X2, ..., Xm-1, Xm)

6

1. Zdefiniowanie

wielko

ś

ci mierzonej

Raport z pomiarów

Start

4. Wybór metody pomiaru i

przyrz

ą

dów pomiarowych

Raport z pomiarów

Procedura ogólna szacowania niepewno

ś

ci pomiaru

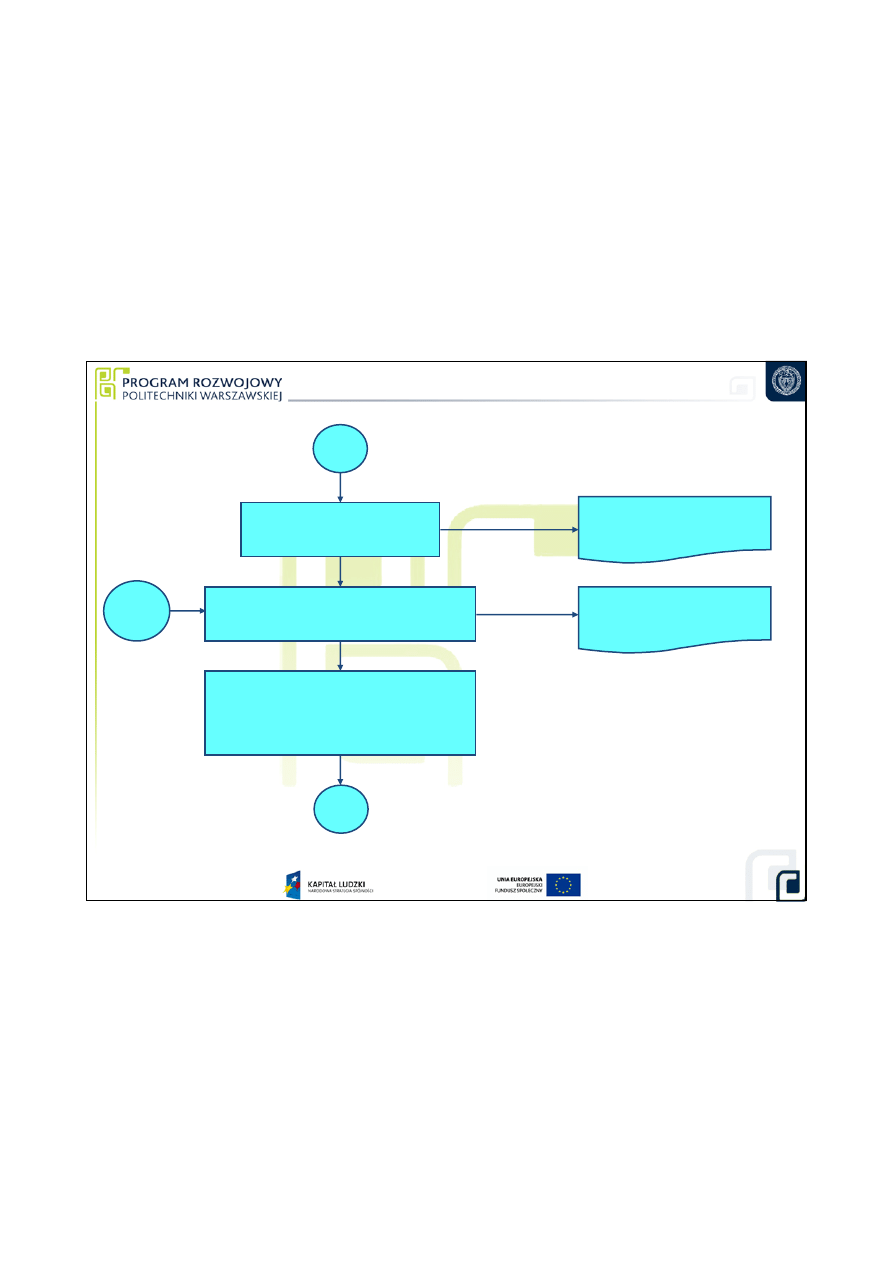
8. Oszacowanie niepewno

ś

ci

standardowych wielko

ś

ci

wej

ś

ciowych i wpływaj

ą

cych

9

6. Wykonanie

pomiaru (pomiarów)

Raport z pomiarów

(wyniki surowe)

5

7. Wyznaczenie poprawek

(obliczanie wyniku pomiaru)

Raport z pomiarów

(wyniki poprawione)

13

Procedura ogólna szacowania niepewno

ś

ci pomiaru

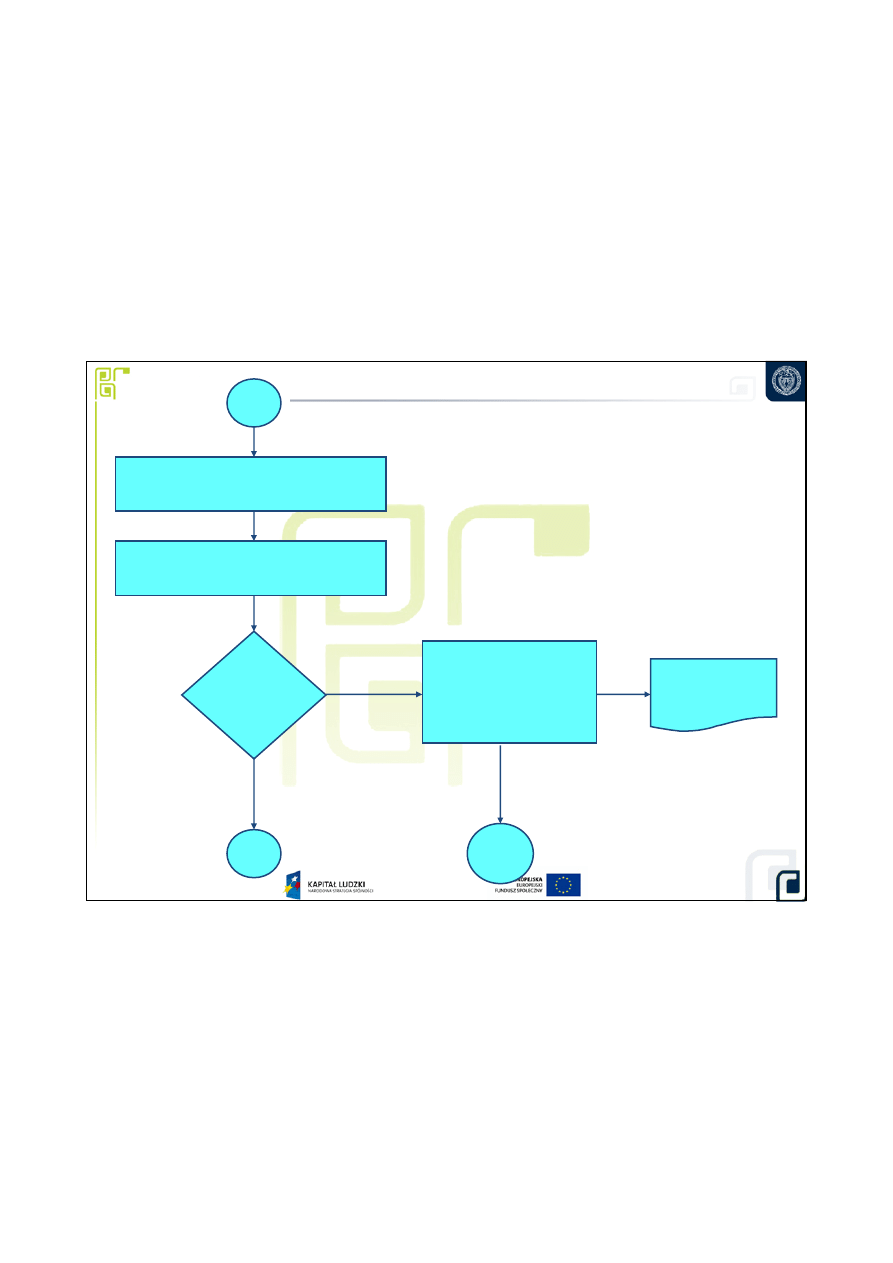
9. Wyznaczenie standardowej

niepewno

ś

ci zło

ż

onej

8

10. Wyznaczenie niepewno

ś

ci

rozszerzonej U(Y)

Czy

U(Y)

≤≤≤≤

Udop

11. Sformułowanie

ko

ń

cowej postaci

wyniku

Koniec

Raport z

pomiarów

TAK

12

NIE

Procedura ogólna szacowania niepewno

ś

ci pomiaru

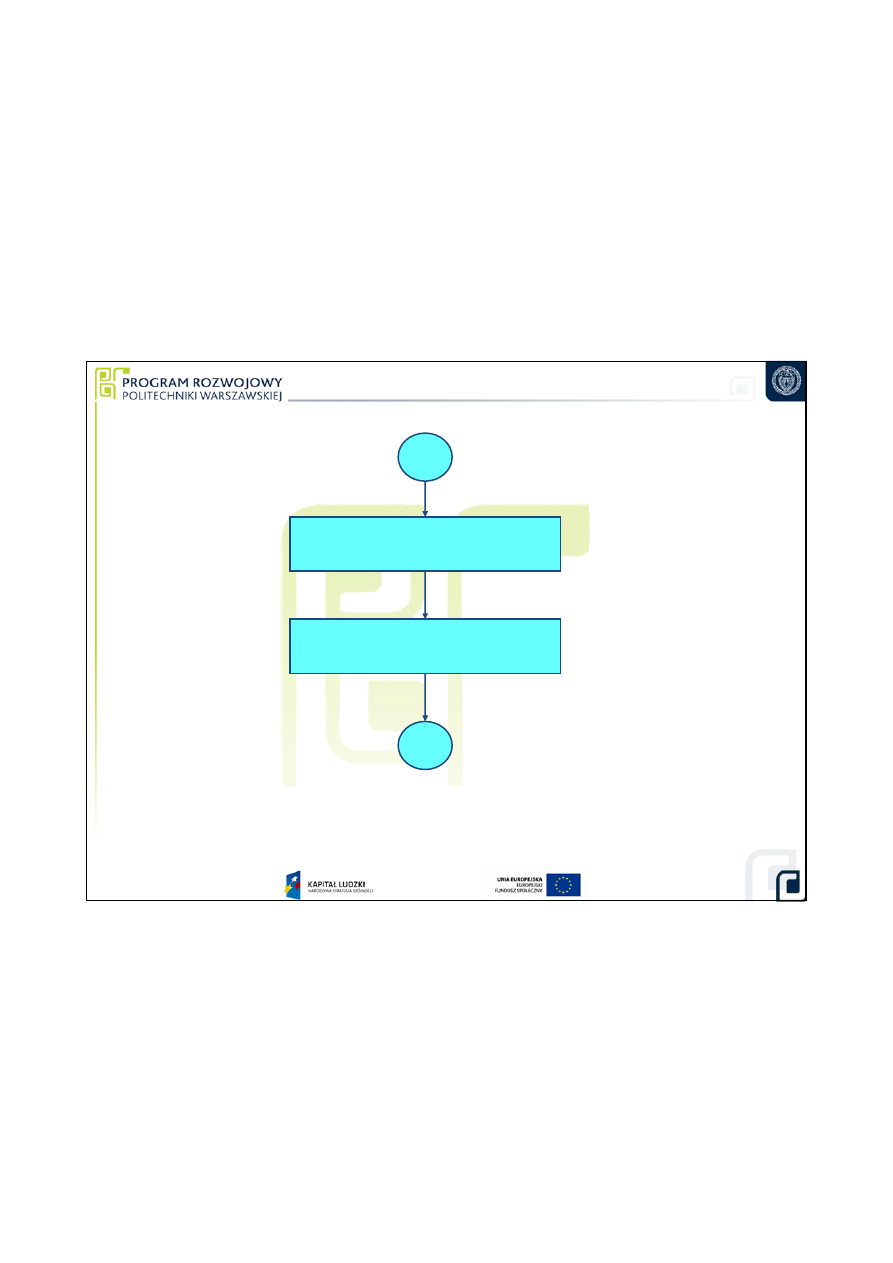
12. Analiza wpływu

poszczególnych składowych

10

13. Wykonanie

dodatkowych pomiarów

7

Procedura ogólna szacowania niepewno

ś

ci pomiaru

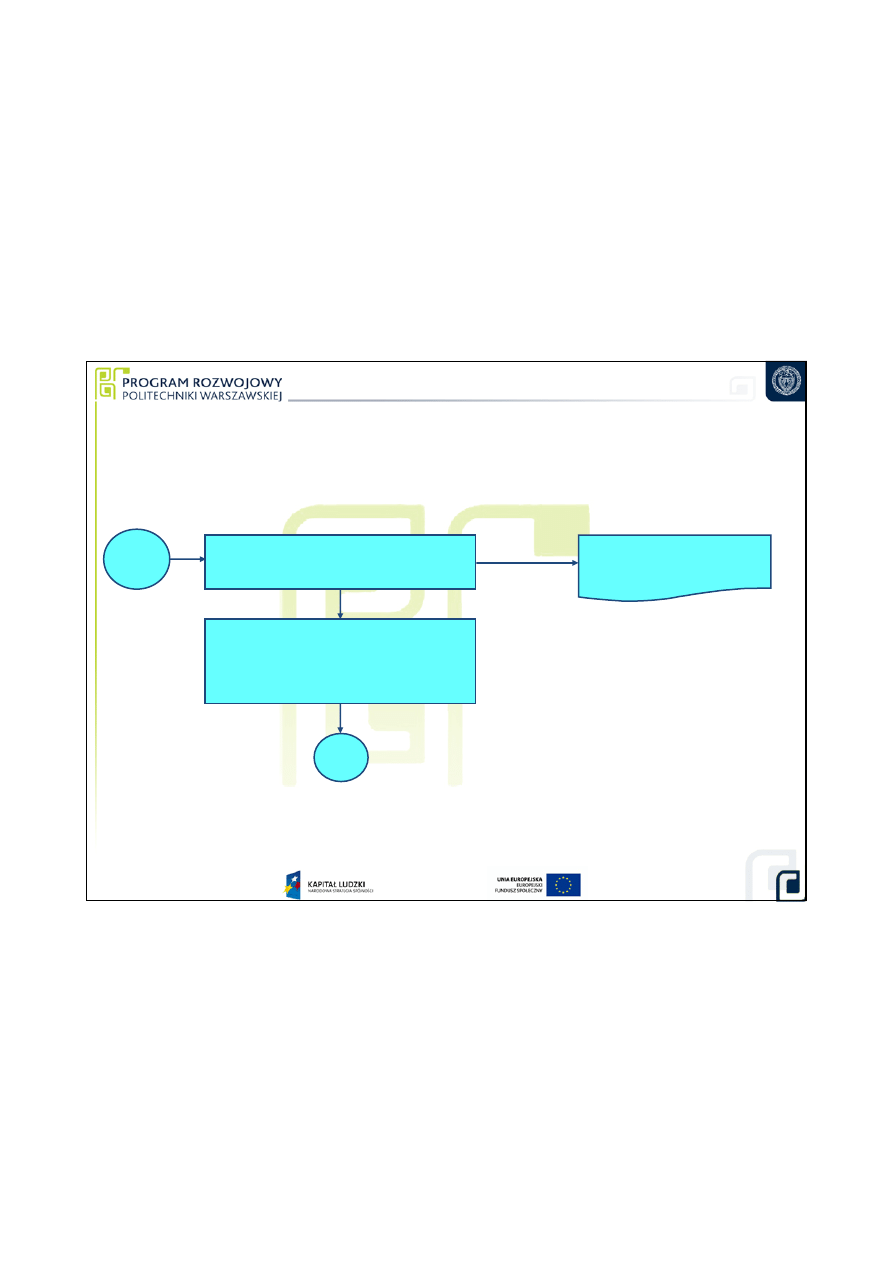
8. Oszacowanie niepewno

ś

ci

standardowych wielko

ś

ci

wej

ś

ciowych i wpływaj

ą

cych

9

7. Wyznaczenie poprawek

(obliczanie wyniku pomiaru)

Raport z pomiarów

(wyniki poprawione)

13

Procedura ogólna szacowania niepewno

ś

ci pomiaru

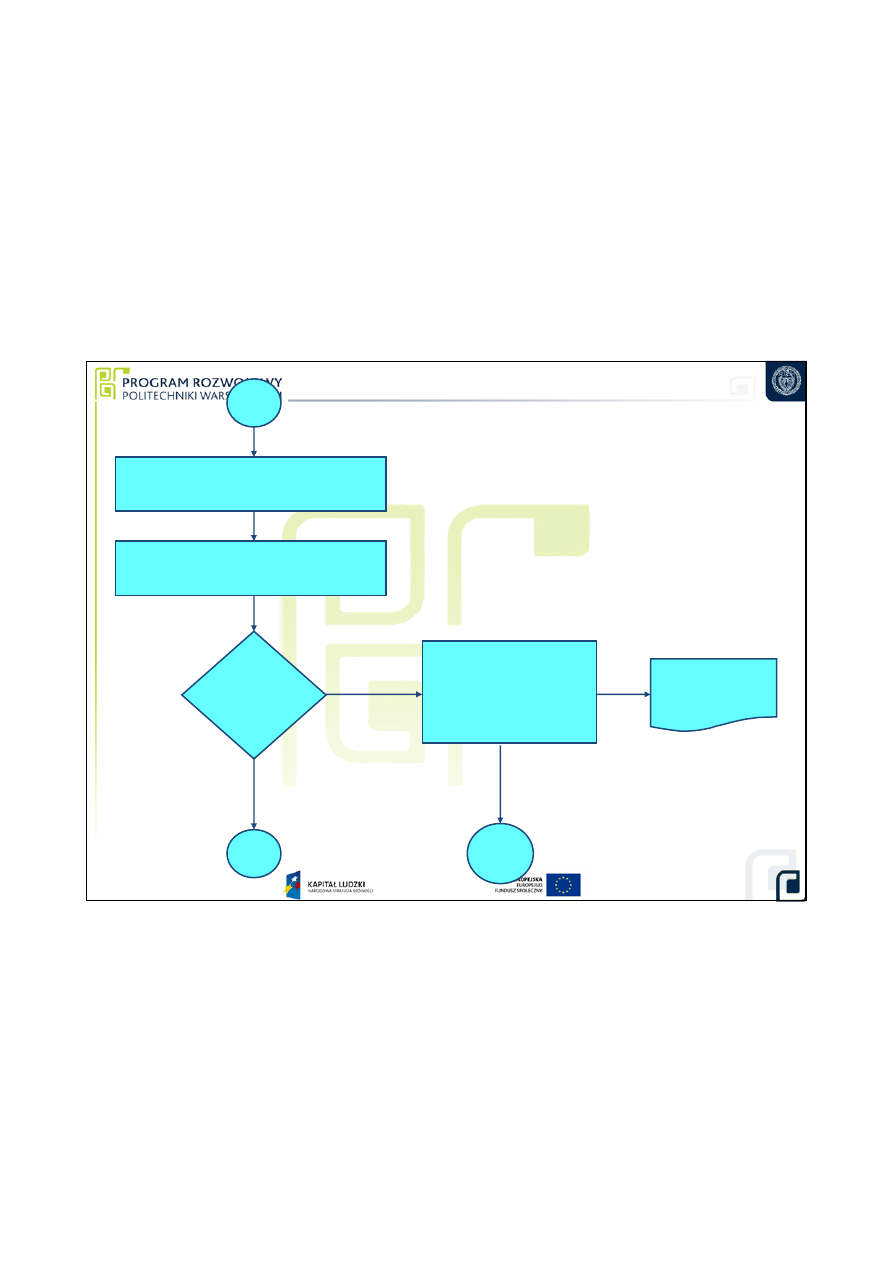
9. Wyznaczenie standardowej

niepewno

ś

ci zło

ż

onej

8

10. Wyznaczenie niepewno

ś

ci

rozszerzonej U(Y)

Czy

U(Y)

≤≤≤≤

Udop

11. Sformułowanie
ostatecznej postaci

wyniku

Koniec

Raport z

pomiarów

TAK

12

NIE

Procedura ogólna szacowania niepewno

ś

ci pomiaru

POMIAR SUWMIARKĄ

ELEKTRONICZNĄ

Przykłady realizacji procedury

szacowania niepewno

ś

ci pomiarów

Zadanie pomiarowe nr 1

Zmierzy

ć

wymiar zewn

ę

trzny oznaczony na rysunku symbolem 60h12 (T = 0,300 mm)

Dopuszczalna niepewno

ść

pomiaru, Udop= 0,030 mm.

Do pomiaru wybrano suwmiark

ę

elektroniczn

ą

o zakresie pomiarowym (0 – 150) mm

i rozdzielczo

ś

ci d = 0,01 mm;

ś

w. wzorcowania:

;

)

3

0

(

C

t

°

±

=

∆

mm

0,020

E

E

g

w

=

≤

mm;

0,0075

(W)

p

=

u

1

6

10

)

5

,

1

5

,

11

(

−

−

°

∗

∗

±

=

C

α

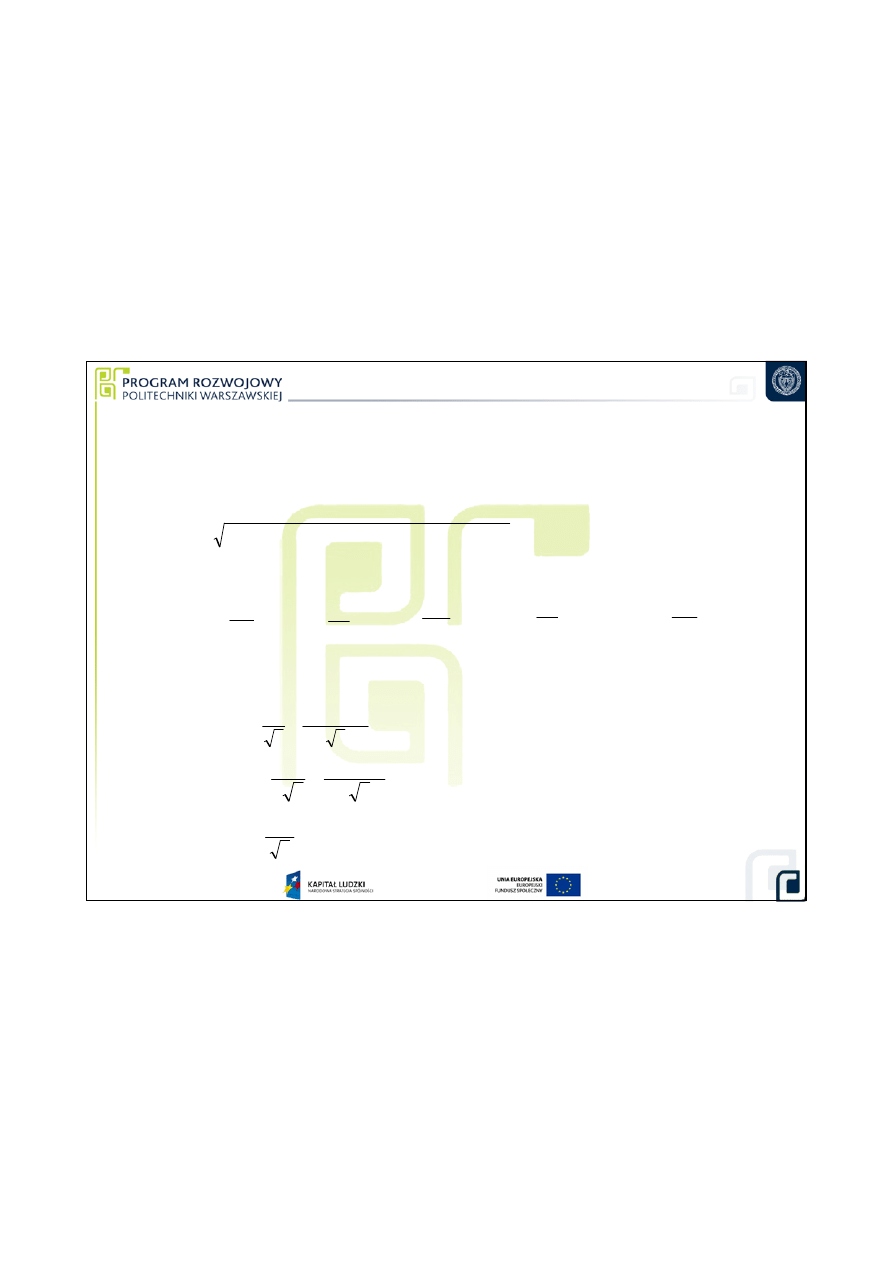
1. Równanie pomiaru

2. Równanie niepewno

ś

ci pomiaru

2.1. Współczynniki wpływu

2.2. Niepewno

ś

ci standardowe składowe

u(W) = u

p

(W) = 0,0075 mm

t

αδ

W

P

P

W

L

rw

w

+

+

+

=

( )

( )

( )

( )

( )

t

u

c

P

u

c

P

u

c

W

u

c

L

u

rw

w

δ

2

2

4

2

2

3

2

2

2

2

2

1

+

+

+

=

1

1

≈

∂

∂

=

W

L

c

1

3

=

∂

∂

=

rw

P

L

c

1

2

=

∂

∂

=

w

P

L

c

C

mm

°

=

∗

=

∂

∂

=

00069

,

0

4

α

δ

W

t

L

c

mm

mm

01155

,

0

3

020

,

0

3

)

(

=

=

=

Eg

P

u

w

mm

mm

0029

,

0

3

2

01

,

0

3

2

)

(

=

=

=

d

P

u

rw

C

C

°

=

°

=

73

,

1

3

3

)

( t

u

δ

Pomiar suwmiark

ą

elektroniczn

ą

Bud

ż

et niepewno

ś

ci pomiaru

Wielko

ść

Oszaco-

wanie

Szeroko

ść

po

ł

ówkowa

Wsp.

rozrzut

u

Niepewn.

stand.

Wsp.

wp

ł

ywu

Sk

ł

adowe

niepewn.

z

ł

o

ż

onej

1

2

3

4

5

6

7

X

i

x

i

0,5R

i

k

*

u(X

i

)

c

i

u

i

(Y)

W

59,84

-

-

0,0075

1

0,0075

P

W

0

0,020

0,01155

1

0,01155

P

rw

0

0,005

0,0029

1

0,0029

δ

t

0

3

1,73

0,00069

0,00119

L

59,84

0,0141

3

3

3

Niepewno

ść

rozszerzona:

U(L) = 2 u(L) = 0,0282 mm

≈≈≈≈

0,028 mm < 0,030 mm

Pomiar suwmiark

ą

elektroniczn

ą

Pomijaj

ą

c w bud

ż

ecie trzeci

ą

składow

ą

(od rozdzielczo

ś

ci

przyrz

ą

du) otrzymamy:

U(L) = 2 u(L) = 0,02765 mm

≈≈≈≈

0,028 mm

Ko

ń

cowy wynik pomiaru:

L = (59,840 ± 0,028) mm

Pomiar suwmiark

ą

elektroniczn

ą

Długo

ść

mierzonego elementu zawiera si

ę

w dopuszczalnych

granicach (59,70 ÷ 60,00) mm

POMIAR MIKROMETREM

Zadanie pomiarowe nr 2

Zmierzy

ć

wymiar zewn

ę

trzny, oznaczony na rysunku symbolem 25h9 (T=0,052 mm);

dopuszczalna niepewno

ść

pomiaru: Udop= 0,005 mm.

Do pomiaru wybrano mikrometr analogowy o zakresie pomiarowym (0 – 25) mm
i warto

ś

ci działki elementarnej 0,01 mm;

ś

w. wzorcowania: Ek = 4,5 µm, U(E) = 1,5 µm

Przykłady szacowania

niepewno

ś

ci pomiarów

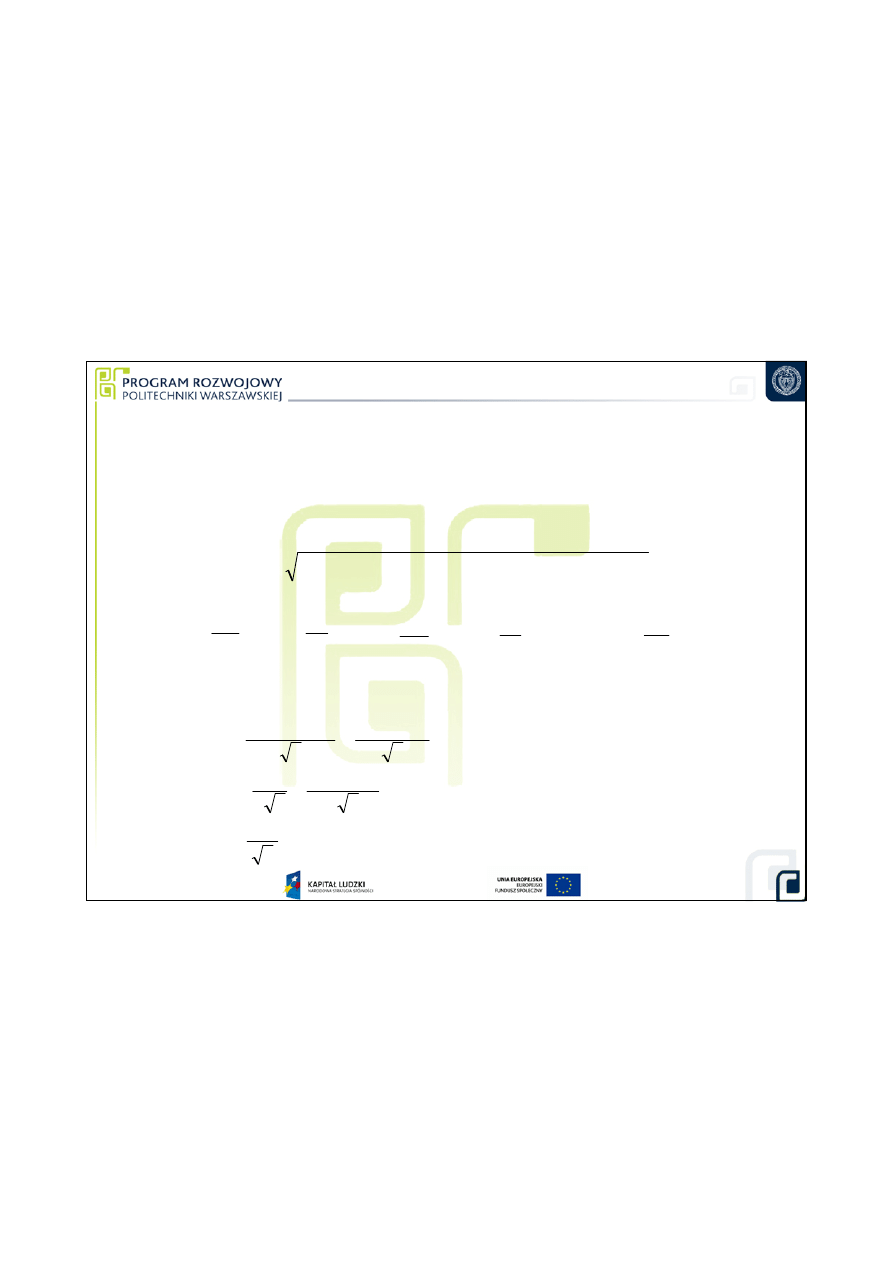
Obliczenia:

1

. Równanie pomiaru

2. Równanie niepewno

ś

ci pomiaru

2.1. Współczynniki wpływu

2.2. Niepewno

ś

ci standardowe składowe

u(W)=u

p

(W) = 0,0006 mm

t

αδ

W

P

P

W

D

rw

w

+

+

+

=

( )

( )

( )

( )

( )

t

u

c

P

u

c

P

u

c

W

u

c

D

u

rw

w

δ

2

2

4

2

2

3

2

2

2

2

2

1

+

+

+

=

1

1

=

∂

∂

=

W

D

c

x

1

3

=

∂

∂

=

rw

P

D

c

1

2

=

∂

∂

=

w

P

D

c

C

mm

°

=

∗

=

∂

∂

=

000288

,

0

4

α

δ

W

t

D

c

mm

mm

00346

,

0

3

006

,

0

3

)

(

)

(

=

=

+

=

w

k

w

E

U

E

P

u

mm

mm

00029

,

0

3

2

001

,

0

3

2

)

(

=

=

=

d

P

u

rw

C

C

°

=

°

=

73

,

1

3

3

)

( t

u

δ

Pomiar mikrometrem

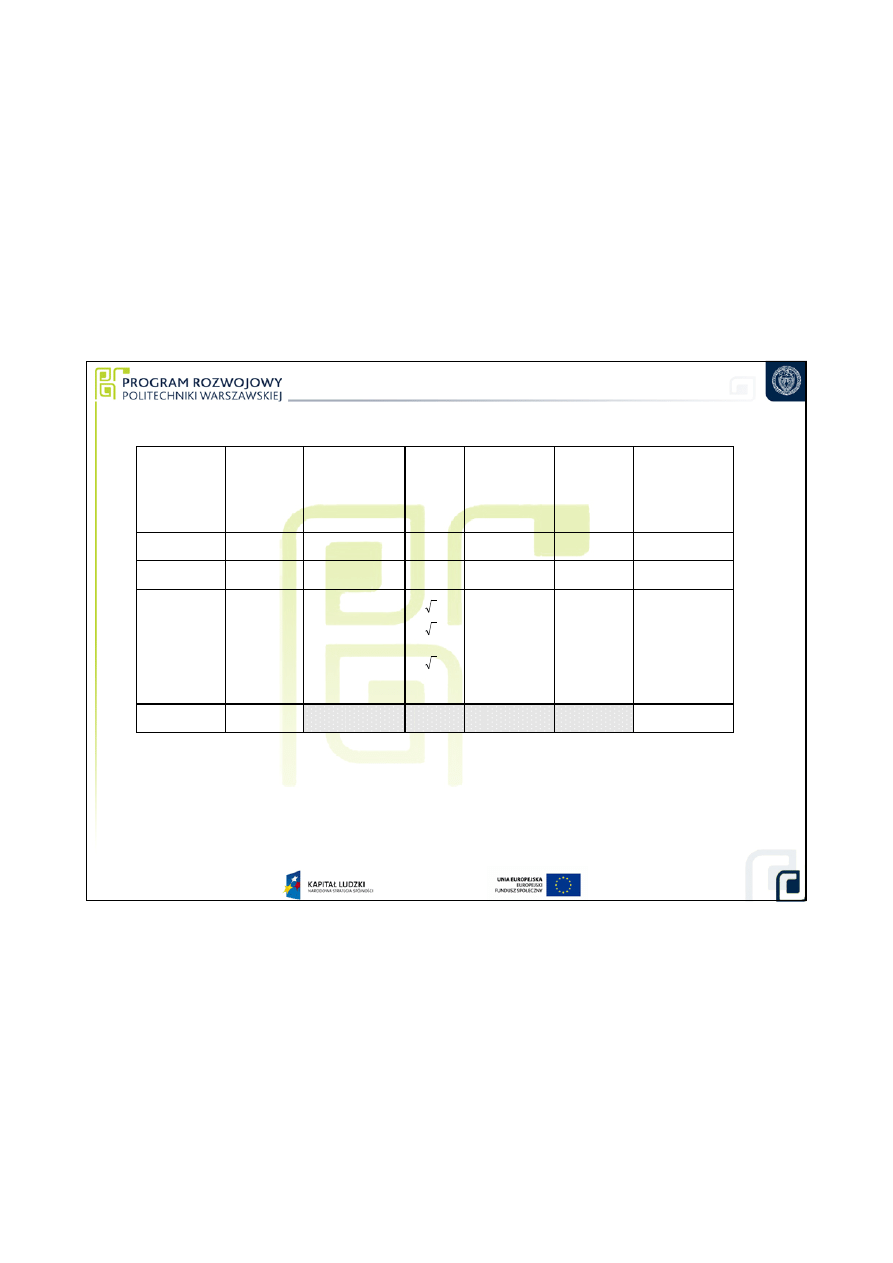
Bud

ż

et niepewno

ś

ci pomiaru:

Wielkość

Oszaco-

wanie

Szerokość

połówkowa

Wsp.

rozrzutu

Niepewn.

stand.

Wsp.

wpływu

Składowe

niepewn.

złożonej

1

2

3

4

5

6

7

X

i

x

i

0,5R

i

k

*

u(X

i

)

c

i

u

i

(Y)

W

24,975

-

-

0,0006

1

0,0006

P

W

0

0,006

0,00346

1

0,00346

P

rw

0

0,0005

0,0003

1

0,0003

δ

t

0

3

1,73

0,000288

0,0005

D

24,975

0,00356

3

3

3

U(D) = 2 u(D) = 0,00712 mm

≈≈≈≈

0,007 mm >

U

dop

= 0,005 mm

U(D) = 1,65 u(D) = 0,005874 mm

≈≈≈≈

0,006 mm > 0,005 mm

Rozkład wynikowy zbliżony do dominującego rozkładu prostokątnego

Pomiar mikrometrem

Pomijaj

ą

c w bud

ż

ecie trzeci

ą

składow

ą

(od rozdzielczo

ś

ci przyrz

ą

du)

otrzymamy:

U(D) = 1,65 u(D) = 1,65*0,00355 mm

≈≈≈≈

0,006 mm >

U

dop

Nie jest spełnione wymaganie dotycz

ą

ce niepewno

ś

ci

dopuszczalnej ze wzgl

ę

du na zbyt du

ż

e bł

ę

dy wskazania

zastosowanego mikrometru.

Zastosowano wi

ę

c do pomiaru mikrometr elektroniczny, który miał

w

ś

wiadectwie potwierdzenie zgodno

ś

ci z PN-82/M-53200

i otrzymano nowy bud

ż

et.

Pomiar mikrometrem

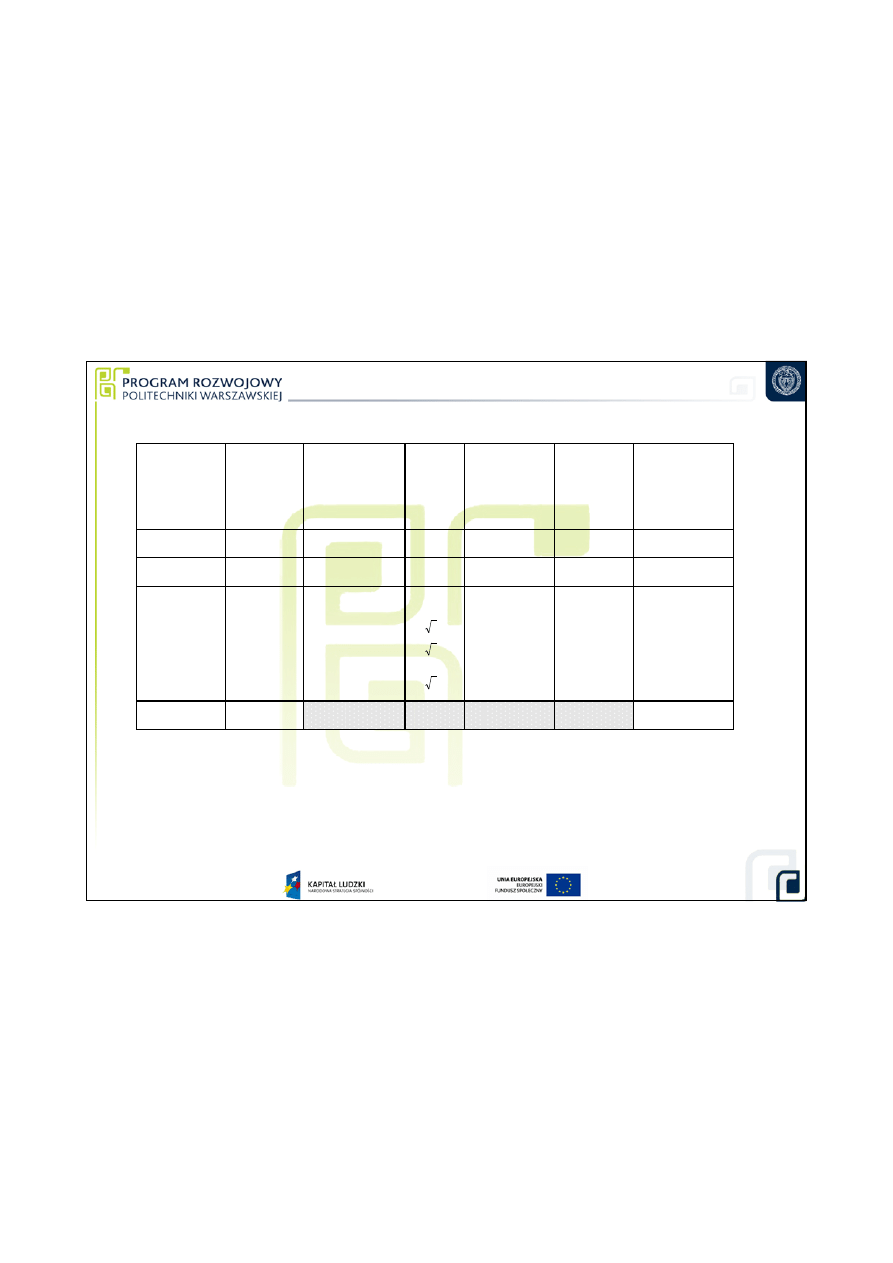
Bud

ż

et niepewno

ś

ci pomiaru:

Wielkość

Oszaco-

wanie

Szerokość

połówkowa

Wsp.

rozrzutu

Niepewn.

stand.

Wsp.

wpływu

Składowe

niepewn.

złożonej

1

2

3

4

5

6

7

X

i

x

i

0,5R

i

k

*

u(X

i

)

c

i

u

i

(Y)

W

24,975

-

-

0,0005

1

0,0005

P

W

0

0,004

0,00231

1

0,00231

P

rw

0

0,0005

0,0003

1

0,0003

δ

t

0

3

1,73

0,000288

0,0005

D

24,975

0,002434

3

3

3

U(D) = 2 u(D) = 0,00487 mm

≈≈≈≈

0,005 mm =

Udop

= 0,005 mm

U(D) = 1,65 u(D) = 0,00402 mm

≈≈≈≈

0,004 mm < 0,005 mm

Rozkład wynikowy zbliżony do dominującego rozkładu prostokątnego

Pomiar mikrometrem

Pomijaj

ą

c w bud

ż

ecie trzeci

ą

składow

ą

(od rozdzielczo

ś

ci przyrz

ą

du)

otrzymamy:

U(D) = 1,65 u(D) = 0,003986 mm

≈≈≈≈

0,004 mm

Ko

ń

cowy wynik pomiaru:

D = (24,975 ± 0,004) mm

Ś

rednica mierzonego elementu zawiera si

ę

w dopuszczalnych

granicach (24,948 ÷ 25,000) mm

Pomiar mikrometrem

Potrzebny jest wzorzec długo

ś

ci o wymiarze nominalnym

l

n

= 20,365 mm; U

dop

= 0,001 mm.

Zadanie pomiarowe nr 3

Do budowy stosu wykorzystano płytki wzorcowe z kompletu klasy 2.

W

ś

wiadectwie wzorcowania kompletu płytek było potwierdzenie

zgodno

ś

ci z wymaganiami normy PN-EN ISO 3650

Przy obliczaniu długo

ś

ci stosu wykorzystano graniczne bł

ę

dy

dopuszczalne długo

ś

ci poszczególnych płytek.

Szacowanie niepewno

ś

ci

wyznaczenia długo

ś

ci stosu płytek

Stos o długo

ś

ci nominalnej 20,365 mm

zło

ż

ono z płytek klasy 2 wymienionych w tablicy:

Lp.

D

ł

ugo

ść

nominalna

p

ł

ytki

l

ni

mm

Odchy

ł

ki graniczne

d

ł

ugo

ś

ci

±

t

e

µ

m

1

1,005

0,45

2

1,06

0,45

3

1,3

0,45

4

2

0,45

5

15

0,6

Obliczenie długo

ś

ci stosu na podstawie odchyłek

granicznych długo

ś

ci poszczególnych płytek

W tym przypadku zakresy zmienno

ś

ci zawieraj

ą

si

ę

w przedziałach odchyłek

granicznych, a poprawki długo

ś

ci nie przekraczaj

ą

granic tych przedziałów.

1. Wzór na długo

ść

stosu:

2. Niepewno

ść

standardowa zło

ż

ona:

gdzie:

(

) ( )

L

U

n

n

n

n

±

+

+

+

+

+

+

+

+

+

=

5

4

3

n3

2

1

P

l

P

l

P

l

P

l

P

l

L

5

4

2

1

( )

( )

( )

( )

( )

( )

5

2

4

2

3

2

2

2

2

1

2

P

u

P

u

P

u

P

u

P

u

L

u

+

+

+

+

=

3

ei

i

t

P

u

=

)

(

Obliczenie długo

ś

ci stosu na podstawie odchyłek

granicznych długo

ś

ci poszczególnych płytek

Bud

ż

et niepewno

ś

ci pomiaru

Wielkość

Oszaco-
wanie

Szerokość
połówkowa

Wsp.

rozrzutu

Niepewn.
stand.

Wsp.
wpływu

Składowe

niepewn.

złożonej

1

2

3

4

5

6

7

X

i

x

i

0,5R

i

k

*

u(X

i

)

c

i

u

i

(Y)

l

n1

1,005

-

-

-

-

-

P

1

0

0,00045

0,00026

1

0,00026

l

n2

1,06

-

-

-

-

-

P

2

0

0,00045

0,00026

1

0,00026

l

n3

1,3

-

-

-

-

-

P

3

0

0,00045

0,00026

1

0,00026

l

n4

2

-

-

-

-

-

P

4

0

0,00045

0,00026

1

0,00026

l

n5

15

-

-

-

-

-

P

5

0

0,0006

0,00035

1

0,00035

L

20,365

0,000627

3

3

3

3

3

U(L) = 2 u(L) = 0,001254 mm

≈

0,0013 mm

Długo

ść

stosu płytek wynosi

L = (20,3650 ± 0,0013) mm

Nie jest spe

ł

nione wymaganie

U(L) ≤ 0,001mm

Obliczenie długo

ś

ci stosu na podstawie odchyłek

granicznych długo

ś

ci poszczególnych płytek

Stos o długo

ś

ci nominalnej 20,365 mm zło

ż

ono z płytek wymienionych w tablicy:

Lp.

Długość nominalna

płytki

l

ni

mm

Poprawka długości

ś

rodkowej

P

ci

µ

m

Niepewność

pomiaru

U(P

ci

)

µ

m

1

1,005

+0,35

0,20

2

1,06

-0,22

0,20

3

1,3

-0,15

0,20

4

2

+0,25

0,20

5

15

-0,30

0,24

Tolerancja zmienno

ś

ci długo

ś

ci ww. płytek - t

ν

= 0,3

µ

m

W zwi

ą

zku z negatywnym wynikiem pierwszej analizy, zdecydowano wykorzysta

ć

przy obliczaniu długo

ś

ci stosu poprawki podane w

ś

wiadectwie wzorcowania.

Obliczenie długo

ś

ci stosu płytek z wykorzystaniem poprawek

1. Wzór na długo

ść

stosu:

gdzie:

P

ci

– poprawka długo

ś

ci

ś

rodkowej płytki,

P

ν

i

– poprawka zwi

ą

zana ze zmienno

ś

ci

ą

długo

ś

ci płytki.

2. Wzór na niepewno

ść

standardow

ą

:

3. Niepewno

ś

ci standardowe u(P

ci

) poprawek długo

ś

ci

ś

rodkowych:

4. Niepewno

ś

ci standardowe u(P

ν

i

) poprawek zwi

ą

zanych ze zmienno

ś

ci

ą

długo

ś

ci:

(

) ( )

L

U

P

P

P

P

P

n

n

n

n

±

+

+

+

+

+

+

+

+

+

+

+

+

+

+

=

5

5

4

4

3

2

2

1

1

ν

ν

ν

ν

ν

c5

c4

c3

n3

c2

c1

P

l

P

l

P

l

P

l

P

l

L

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

5

2

5

c

2

4

2

4

c

2

3

2

3

c

2

2

2

2

c

2

1

2

1

c

2

P

u

P

u

P

u

P

u

P

u

P

u

P

u

P

u

P

u

P

u

L

u

ν

ν

ν

ν

ν

+

+

+

+

+

+

+

+

+

=

2

)

(

)

(

ci

ci

P

U

P

u

=

3

2

)

(

i

i

t

P

u

ν

ν

=

Obliczenie długo

ś

ci stosu płytek z wykorzystaniem poprawek

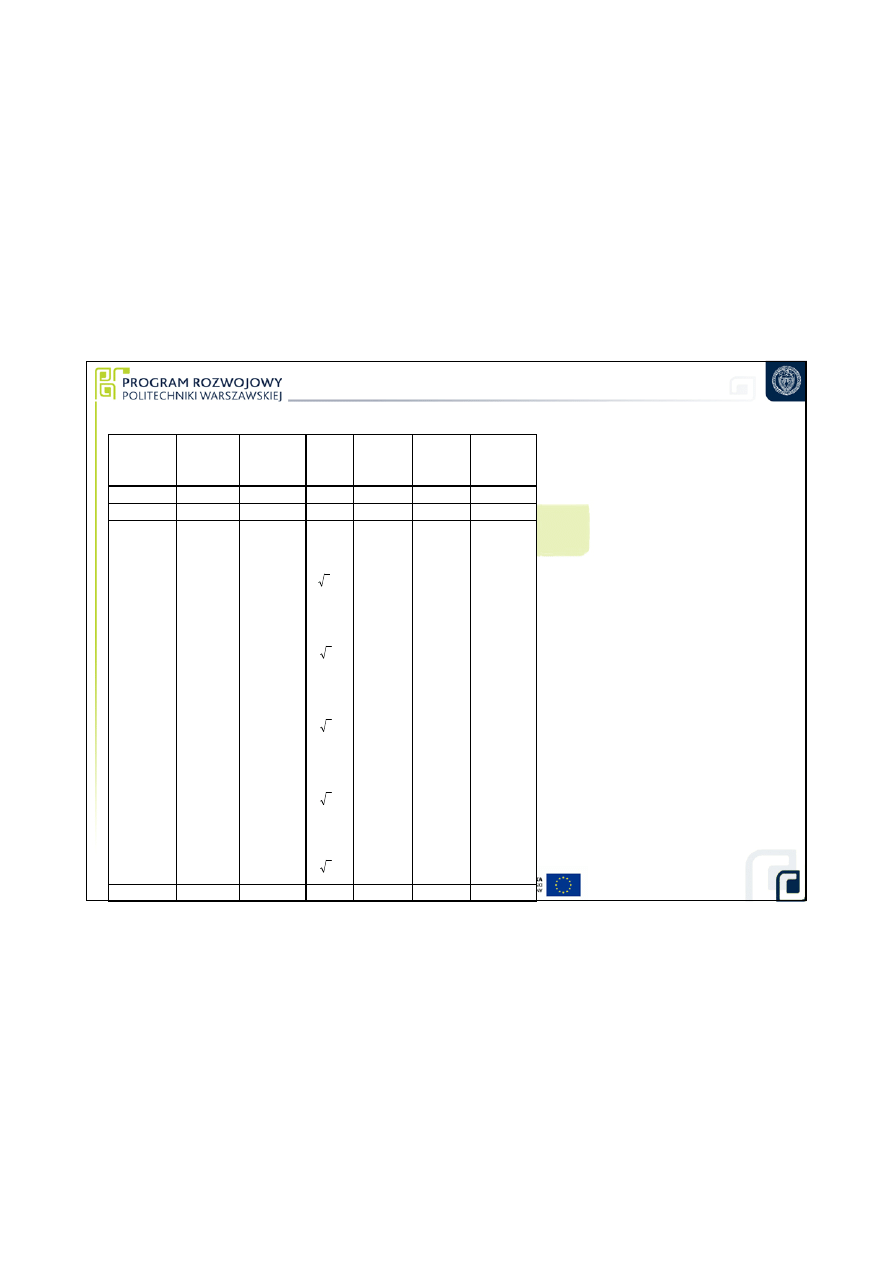
Wielkość

Oszaco-
wanie

Szerokość
połówkow
a

Wsp.

roz-rzu

tu

Niepewn.
stand.

Wsp.
wpływu

Składowe

niepewn.

złożonej

1

2

3

4

5

6

7

X

i

x

i

0,5R

i

k

*

u(X

i

)

c

i

u

i

(Y)

l

n1

1,005

-

-

-

-

-

P

c1

0,00035

0,0002

2

0,0001

1

0,0001

P

ν

1

0

0,00015

0,000087

1

0,000087

l

n2

1,06

-

-

-

-

-

P

c2

-0,00020

0,0002

2

0,0001

1

0,0001

P

ν

2

0

0,000015

0,000087

1

0,000087

l

n3

1,3

-

-

-

-

-

P

c3

-0,00015

0,0002

2

0,0001

1

0,0001

P

ν

3

0

0,00015

0,000087

1

0,000087

l

n4

2

-

-

-

-

-

P

c4

+0,00025

0,0002

2

0,0001

1

0,0001

P

ν

4

0

0,00015

0,000087

1

0,000087

l

n5

15

-

-

-

-

-

P

c5

-0,00030

0,00024

2

0,00012

1

0,00012

P

ν

5

0

0,00015

0,000087

1

0,000087

L

20,36495

0,000304

Bud

ż

et niepewno

ś

ci pomiaru

3

3

3

3

3

U(L) = 2 u(L)

= 0,000607 mm

≈

0,0006 mm < U

dop

= 0,001 mm

Długo

ść

stosu płytek wynosi

L= (20,3650 ± 0,0006) mm

Obliczenie długo

ś

ci stosu płytek z wykorzystaniem poprawek

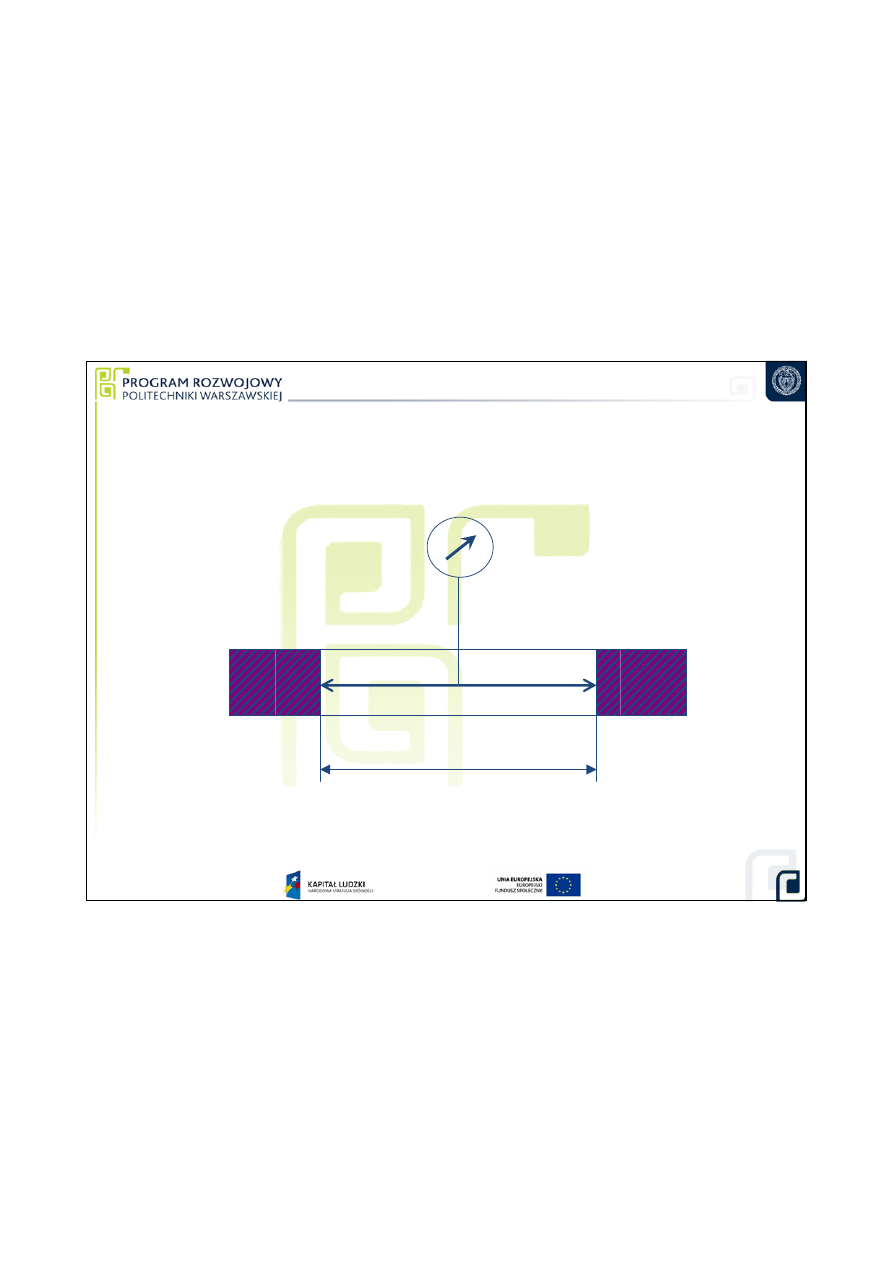
POMIAR

Ś

REDNICY OTWORU Z NIEPEWNO

Ś

CI

Ą

U(D) <= 0,01 mm

D

W

Przykłady szacowania niepewno

ś

ci pomiarów

Równanie pomiaru:

((((

)))) ((((

))))

t

w

w

w

P

L

P

W

P

W

D

++++

++++

++++

−−−−

++++

====

1

1

2

2

gdzie:

W2 – wskazanie przyrz

ą

du na mierzonym otworze,

Pw2 – poprawka wskazania,
W1 - wskazanie przyrz

ą

du na wzorcu pier

ś

cieniowym,

Pw1 - poprawka wskazania,
Lw - wymiar wzorca,
Pt -

poprawka temperaturowa

Pt = L

n

αααα ∆∆∆∆

t

gdzie:

L

n

-

wymiar nominalny wzorca,

α

-

współczynnik rozszerzalno

ś

ci liniowej,

∆∆∆∆

t –

ró

ż

nica temperatur wzorca i elementu mierzonego.

Pomiar

ś

rednicy otworu

t

L

L

P

P

W

P

P

W

D

n

w

w

r

w

r

∆∆∆∆

⋅⋅⋅⋅

++++

++++

−−−−

−−−−

−−−−

++++

++++

====

αααα

1

1

1

2

2

2

gdzie:

P

r2

i P

r1

- poprawki zwi

ą

zane z rozdzielczo

ś

ci

ą

ROZBUDOWANE RÓWNANIE POMIARU:

RÓWNANIE NIEPEWNO

Ś

CI POMIARU:

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

2

2

2

1

2

1

2

1

2

2

2

2

2

2

2

t

u

L

L

u

P

u

P

u

W

u

P

u

P

u

W

u

D

u

n

w

w

r

w

r

∆∆∆∆

⋅⋅⋅⋅

++++

++++

++++

++++

++++

++++

++++

====

αααα

Przyjmuj

ą

c:

u(W

1

)= u(W

2

)= u(W)

u(P

r1

)= u(P

r2

)= u(P

r

)

u(P

w1

)= u(P

w2

)= u(P

w

)

Pomiar

ś

rednicy otworu

)

(

)

(

)

(

)

(

2

)

(

2

)

(

2

)

(

2

2

2

2

2

2

t

u

L

L

u

P

u

P

u

W

u

D

u

n

w

w

r

∆∆∆∆

⋅⋅⋅⋅

++++

++++

++++

++++

====

αααα

RÓWNANIE NIEPEWNO

Ś

CI POMIARU:

Dane do oblicze

ń

:

W

2

= 0,2235 mm

W

1

= 0,1235 mm

L

w

= (100,0008

±

0,0009) mm

L

n

= 100 mm

we = 0,001mm

E

g

=

±

0,003 mm

∆

t = (0 ± 2)

°

C

α

= (11,5

±

1,5)·10

-6

°

C

-1

u

p

(W) = 0,0006 mm

Pomiar

ś

rednicy otworu

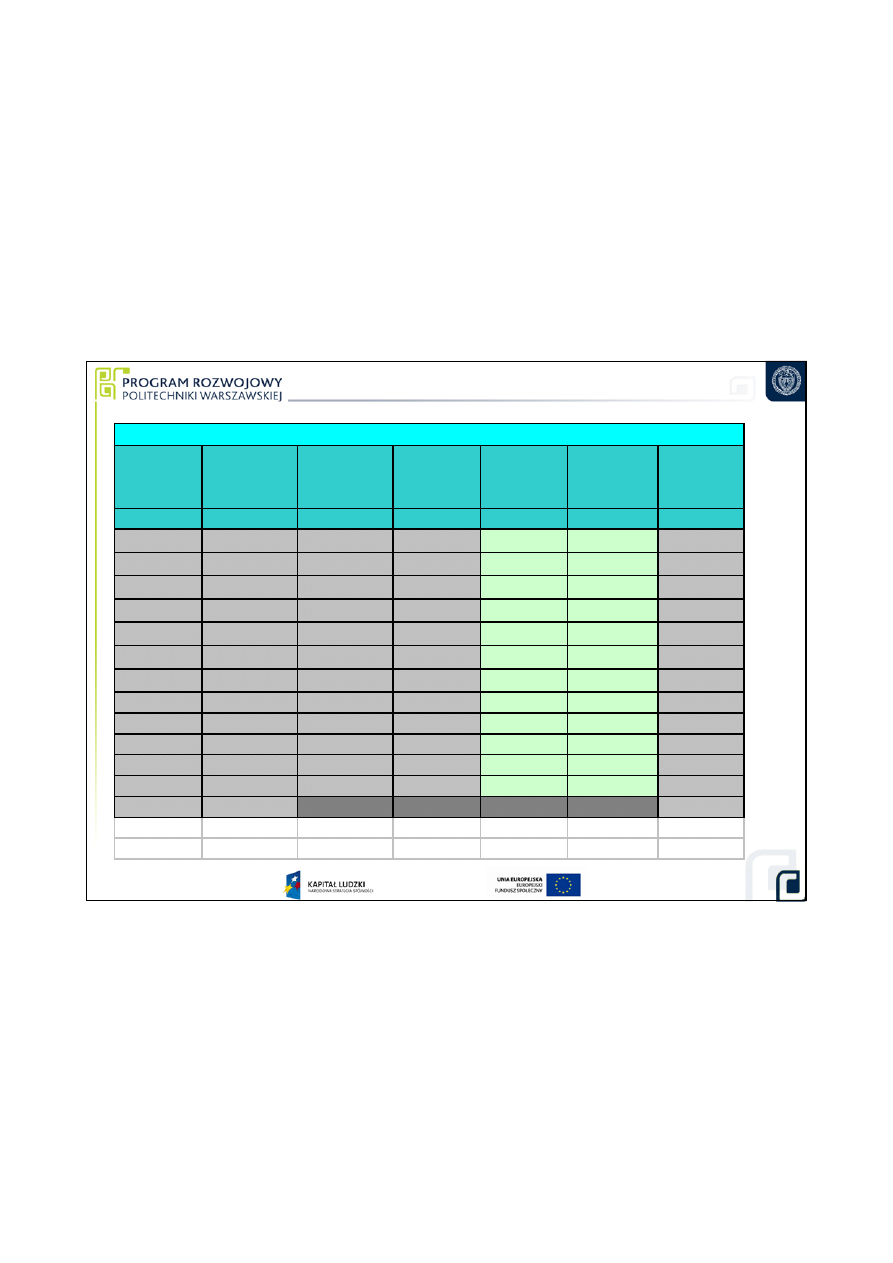
wielko

ść

Oszacowa

nie

Szeroko

ść

połówkowa

Wsp.

Rozrzuty

Niepewn.s

tand.

Wsp.

wpływu

Składowe

niep.
zło

ż

.

1

2

3

4

5

6

7

W

2

0,2235

0,0006

1,00E+00

6,00E-04

P

r2

0

0,0005

1,732051 2,89E-04

1,00E+00

2,89E-04

P

w2

0

3,00E-03

1,732051 1,73E-03

1,00E+00

1,73E-03

W

1

0,1235

0,0006

1,00E+00

6,00E-04

P

r1

0,00E+00

0,0005

1,732051 2,89E-04

1,00E+00

2,89E-04

P

w1

0

3,00E-03

1,732051 1,73E-03

1,00E+00

1,73E-03

L

w

100,0008

0,0009

2 4,50E-04

1,00E+00

4,50E-04

α

α

α

α

0,0000115

1,50E-06

2

0,0000

0,00E+00 0,00E+00

∆

∆∆

∆

t

0

2

1,732051

1,1547

1,15E-03

1,33E-03

D

100,1008

0,002975

0,006

Bud

ż

et niepewno

ś

ci pomiaru

ś

rednicy otworu

Pomiar

ś

rednicy otworu

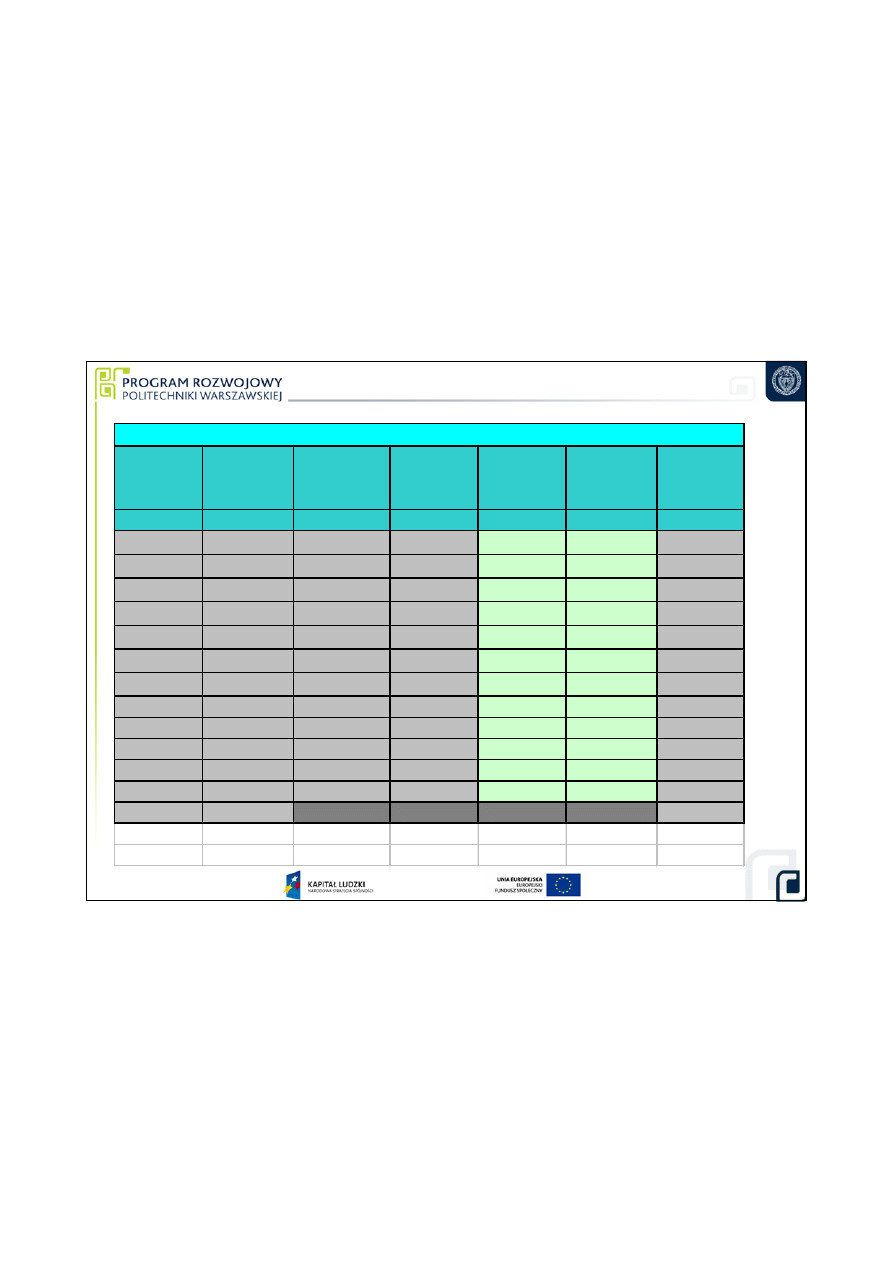
wielko

ść

Oszacowa

nie

Szeroko

ść

połówkowa

Wsp.

Rozrzuty

Niepewn.s

tand.

Wsp.

wpływu

Składowe

niep.
zło

ż

.

1

2

3

4

5

6

7

W

2

0,2235

0,0006

1,00E+00

6,00E-04

P

r2

0

0,0005

1,732051 2,89E-04

0,00E+00 0,00E+00

P

w2

0

3,00E-03

1,732051 1,73E-03

1,00E+00

1,73E-03

W

1

0,1235

0,0006

1,00E+00

6,00E-04

P

r1

0,00E+00

0,0005

1,732051 2,89E-04

0,00E+00 0,00E+00

P

w1

0

3,00E-03

1,732051 1,73E-03

1,00E+00

1,73E-03

L

w

100,0008

0,0009

2 4,50E-04

1,00E+00

4,50E-04

α

α

α

α

1,15E-05

1,50E-06

2

0,0000

0,00E+00 0,00E+00

∆

∆∆

∆

t

0

2

1,732051

1,1547

1,15E-03

1,33E-03

D

100,1008

0,002947

0,006

Bud

ż

et niepewno

ś

ci pomiaru

ś

rednicy otworu

Pomiar

ś

rednicy otworu

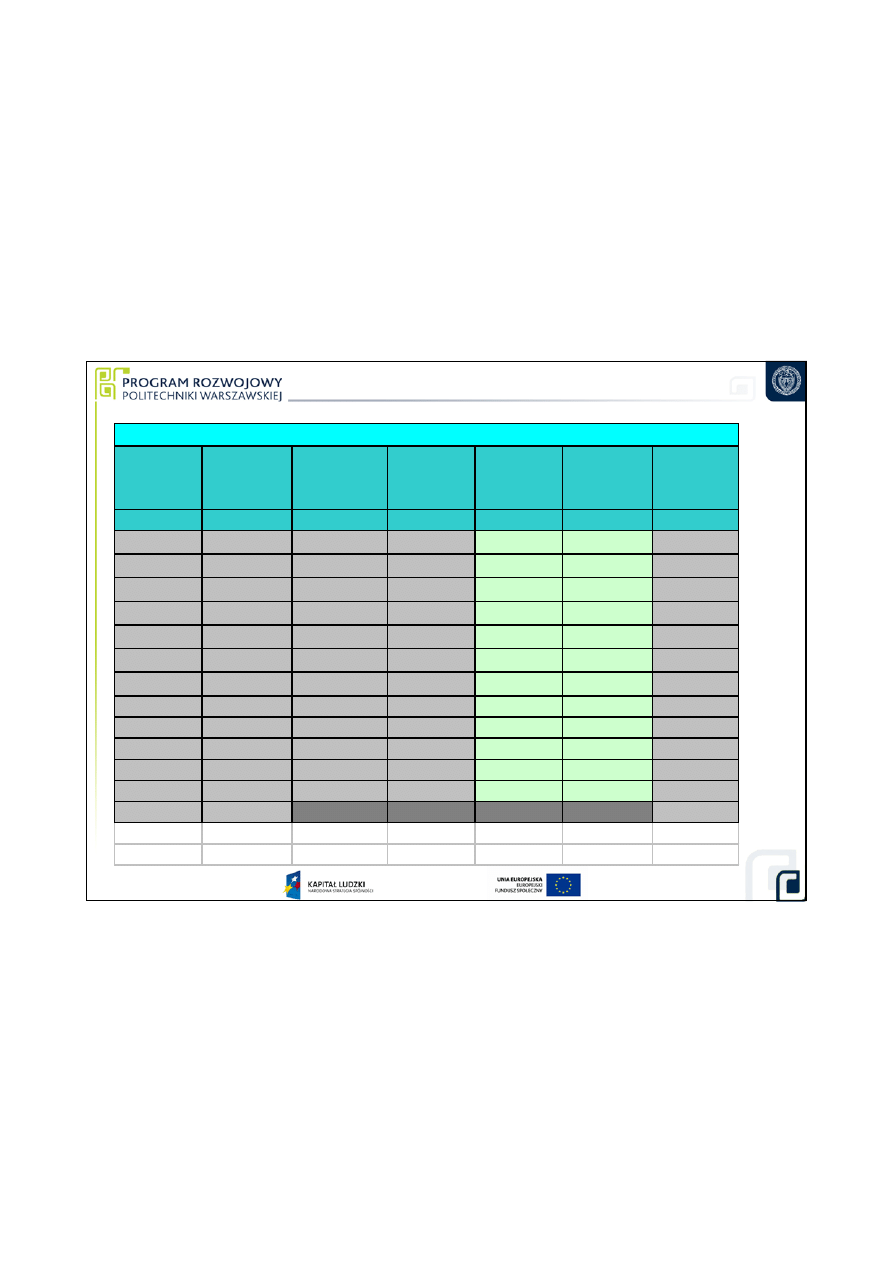
wielko

ść

Oszacowa

nie

Szeroko

ść

połówkowa

Wsp.

Rozrzuty

Niepewn.s

tand.

Wsp.

wpływu

Składowe

niep.
zło

ż

.

1

2

3

4

5

6

7

W

2

0,2235

0,0006

0,00E+00 0,00E+00

P

r2

0

0,0005

1,732051 2,89E-04

0,00E+00 0,00E+00

P

w2

0

3,00E-03

1,732051 1,73E-03

1,00E+00

1,73E-03

W

1

0,1235

0,0006

0,00E+00 0,00E+00

P

r1

0,00E+00

0,0005

1,732051 2,89E-04

0,00E+00 0,00E+00

P

w1

0

3,00E-03

1,732051 1,73E-03

1,00E+00

1,73E-03

L

w

100,0008

0,0009

2 4,50E-04

1,00E+00

4,50E-04

α

α

α

α

1,15E-05

1,50E-06

2

0,0000

0,00E+00 0,00E+00

∆

∆∆

∆

t

0

2

1,732051

1,1547

1,15E-03

1,33E-03

D

100,1008

0,002822

0,006

Bud

ż

et niepewno

ś

ci pomiaru

ś

rednicy otworu

Pomiar

ś

rednicy otworu

Ko

ń

cowy wynik pomiaru:

D = (100,101

±

0,006) mm

U(D) = 0,006 mm < U

dop

= 0,01 mm

Pomiar

ś

rednicy otworu

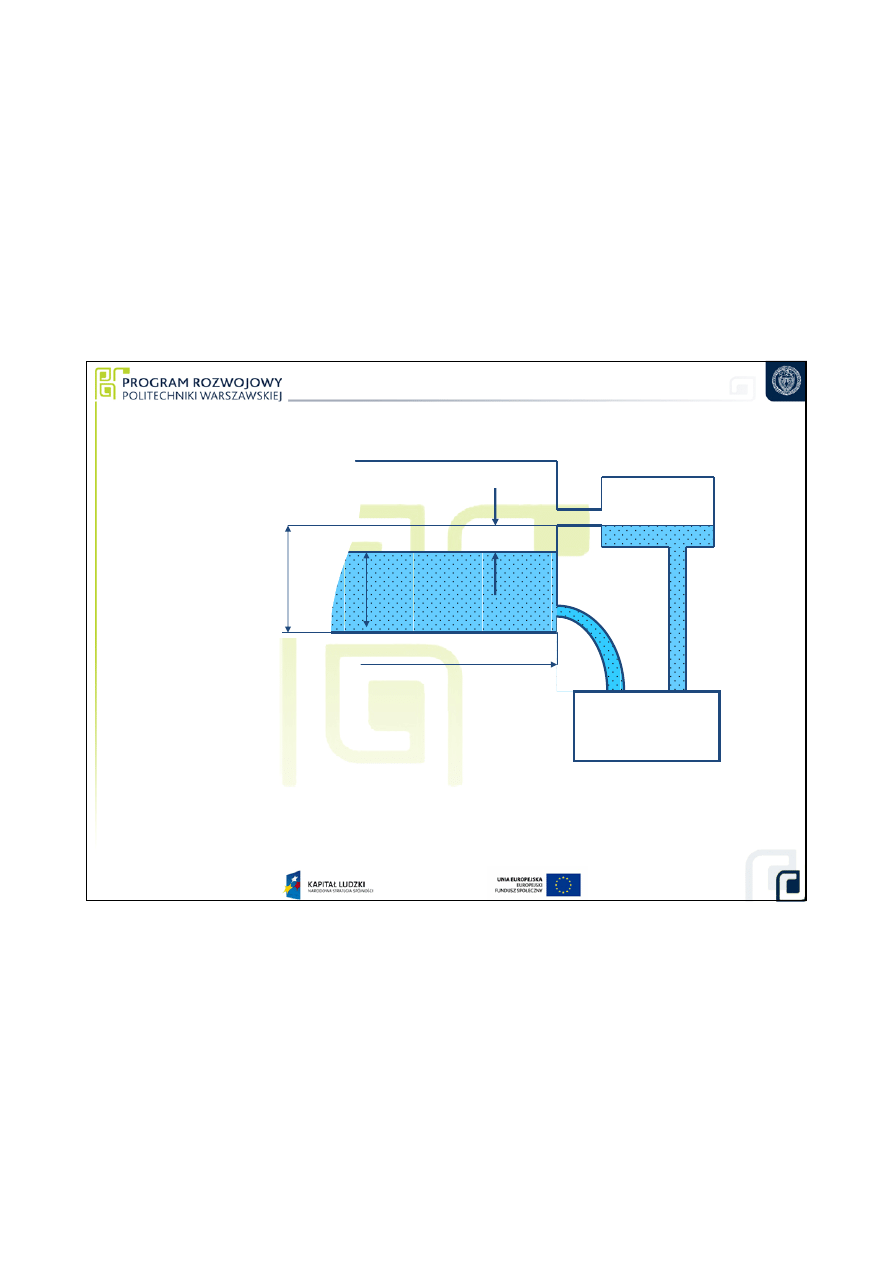
POMIAR OBJ

Ę

TO

ŚĆ

I WODY W KOTLE ENERGETYCZNYM

D = (300,0

±

1,0) cm

H = (200,0

±

1,0) cm

∆∆∆∆

p = (977,0

±

9,8) Pa

ρρρρ

= (0,998

±

0,001) g/cm

3

g = (979

±

4) cm/s

2

Niepewno

ść

wzgl

ę

dna dopuszczalna: 1 %

∆∆∆∆

h

∆∆∆∆

p

H

D

h

Przykłady szacowania niepewno

ś

ci pomiarów

4

2

H

D

V

ππππ

====

Pojemno

ść

zbiornika okre

ś

la wzór:

Poziom wody w zbiorniku:

h = H -

∆∆∆∆

h

Obni

ż

enie poziomu

∆∆∆∆

h wyznacza si

ę

z zale

ż

no

ś

ci:

g

p

h

⋅⋅⋅⋅

∆∆∆∆

====

∆∆∆∆

ρρρρ

Zatem obj

ę

to

ść

wody w zbiorniku okre

ś

la wzór:

((((

))))

h

H

D

V

w

∆∆∆∆

−−−−

====

4

2

ππππ

Pomiar obj

ę

to

ś

ci wody w kotle energetycznym

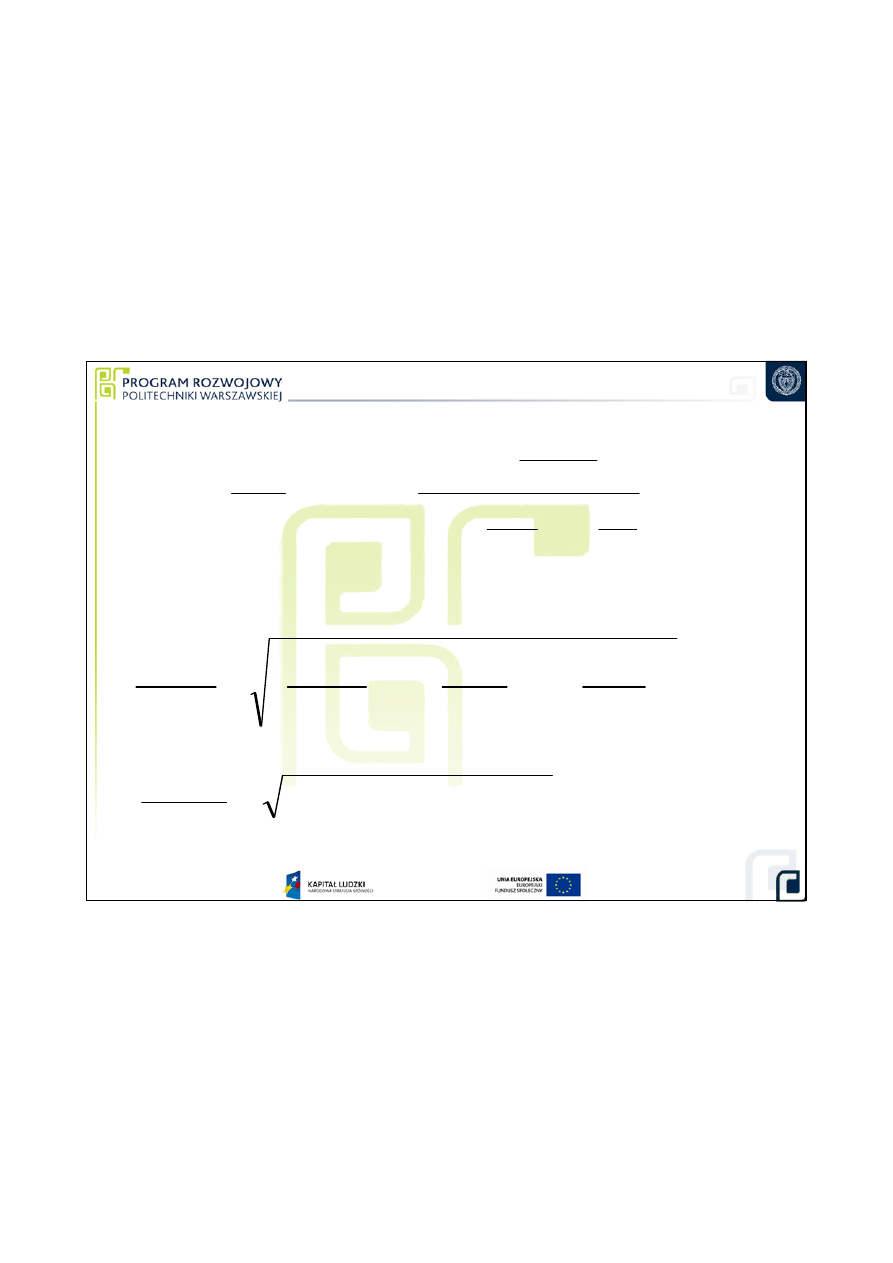
Obliczenie poziomu wody:

cm

s

cm

cm

g

s

cm

g

cm

g

p

H

h

00

,

190

979

998

,

0

9770

200

2

3

2

====

⋅⋅⋅⋅

⋅⋅⋅⋅

−−−−

====

⋅⋅⋅⋅

∆∆∆∆

−−−−

====

ρρρρ

∆∆∆∆

h = 10,00cm ±U(

∆

h); Vw= 13430308,6 cm

3

±U(V);

2

2

2

)

(

)

(

)

(

)

(













++++













++++













∆∆∆∆

====

∆∆∆∆

∆∆∆∆

g

g

u

u

p

p

u

h

h

u

ρρρρ

ρρρρ

(((( ))))

541

,

0

2

,

0

05

,

0

5

,

0

)

(

2

2

2

====

++++

++++

====

∆∆∆∆

∆∆∆∆

h

h

u

Pomiar obj

ę

to

ś

ci wody w kotle energetycznym

Niepewno

ść

standardowa u(

∆

h) wynosi:

u(

∆∆∆∆

h) = 10,00cm ·0,00541= 0,0541cm

h = H -

∆∆∆∆

h

2

2

2

2

054

,

0

5

,

0

)

(

)

(

)

(

+

=

∆

+

=

h

u

H

u

h

u

u(h) = 0,5 cm

4

2

h

D

V

w

ππππ

====

2

2

)

(

)

(

4

)

(













++++













====

h

h

u

D

D

u

V

V

u

w

w

Pomiar obj

ę

to

ś

ci wody w kotle energetycznym

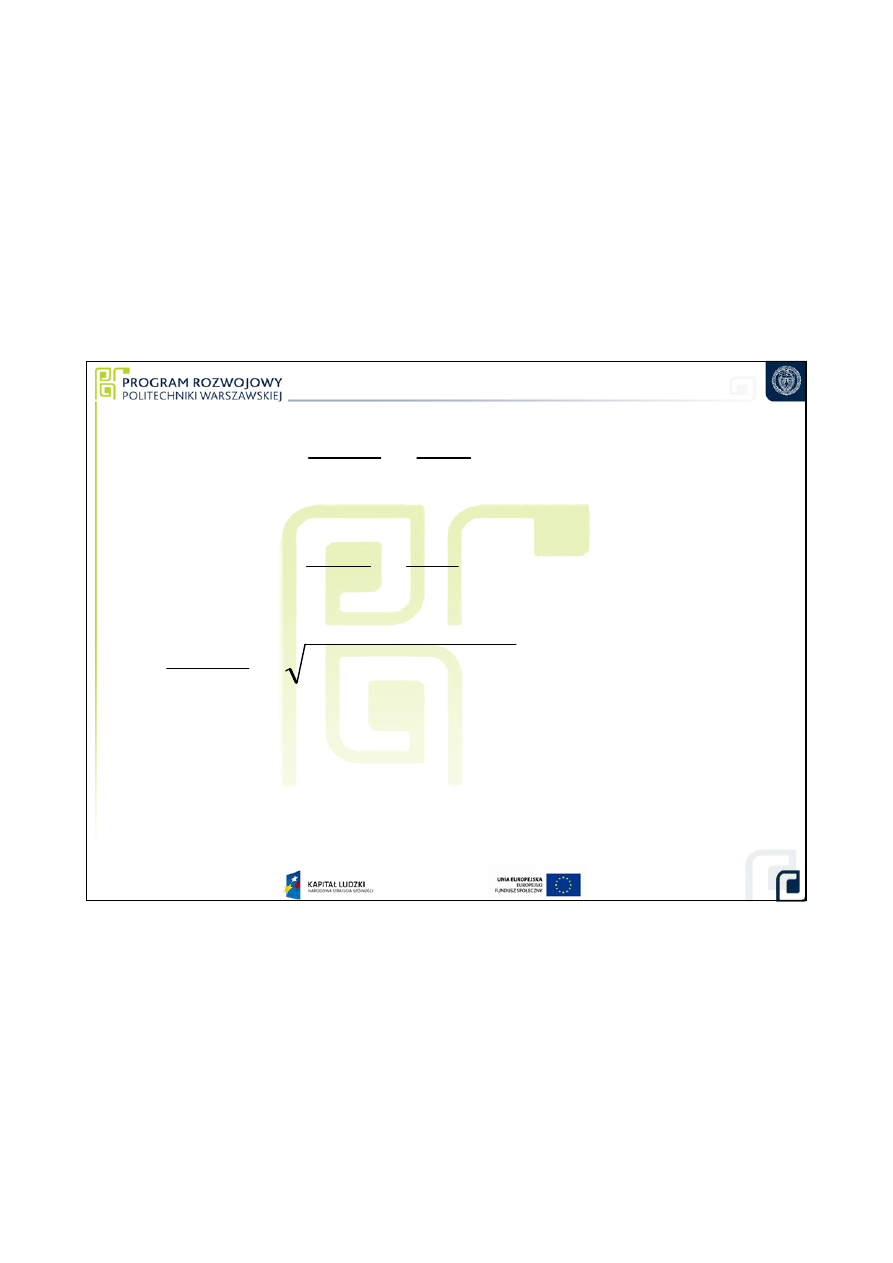
16

,

0

300

5

,

0

)

(

====

====

D

D

u

%

26

,

0

190

5

,

0

)

(

====

====

h

h

u

%

4123

,

0

26

,

0

16

,

0

4

)

(

2

2

====

++++

⋅⋅⋅⋅

====

w

w

V

V

u

%

u(Vw) = 13430308,6 cm

3

· 0,004123 = 55373,16 cm

3

U(Vw) = 2· u(Vw) = 110000 cm

3

= 0,11 m

3

Pomiar obj

ę

to

ś

ci wody w kotle energetycznym

V

w

= (13,43 ± 0,11) m

3

U(V)/V = 0,11/13,43 = 0,82 % < U(V)/Vdop= 1 %

Studenci zechc

ą

opracowa

ć

bud

ż

et niepewno

ś

ci pomiaru dla tego przykładu.

Pomiar obj

ę

to

ś

ci wody w kotle energetycznym

Dzi

ę

kuj

ę

za uwag

ę

i zapraszam na dalsz

ą

cz

ęść

wykładu

Procedura ogólna szacowania

niepewno

ś

ci pomiaru