Krzysztof Pancerz

Algorytmy i struktury danych

Algorytmy i struktury 

danych

WYKŁAD 9 

dr inż. Krzysztof Pancerz

 

Krzysztof Pancerz

Algorytmy i struktury danych

Miara informacji

●

A – zbiór wiadomości wysyłanych przez źródło

●

a – wiadomość ze zbioru A

●

Miara zawartości informacji w wiadomości a:

–

p(a) – prawdopodobieństwo wysłania wiadomości a 

I

=log

2

1

p

a

 

Krzysztof Pancerz

Algorytmy i struktury danych

Entropia

●

A – zbiór wiadomości wysyłanych przez źródło

●

●

Entropia (średnia zawartość informacyjna 

wiadomości):

–

p(a

i

) – prawdopodobieństwo wysłania wiadomości a

i

 

Entropia jest maksymalna dla wiadomości jednakowo 

prawdopodobnych, wówczas                  .



H

=

∑

i

=1

n

p

a

i

log

2

1

p

a

i



A

={a

1,

a

2,

... ,a

n

}



H

=log

2

n

 

Krzysztof Pancerz

Algorytmy i struktury danych

Kodowanie Huffmana

●

W wyniku kodowania Huffmana otrzymujemy zestaw 

kombinacji kodowych o średniej długości zbliżonej do 

średniej zawartości informacyjnej wiadomości 

(entropii).

●

Twierdzenie o kodowaniu źródłowym:

–

Konstrukcja kodu o średniej długości kombinacji 
kodowej mniejszej od entropii źródła nie jest możliwa, 

jeżeli żądamy, aby odbierane dane były dekodowane w 
ujściu danych w sposób jednoznaczny.  

 

Krzysztof Pancerz

Algorytmy i struktury danych

Etapy numerycznego rozwiązywania równania 

nieliniowego

Etap 1

Początkowe  przybliżenie  poszukiwanego  pierwiastka  równania 
nieliniowego  (np.  przedział,  w  którym  znajduje  się  dokładnie  jeden 
pierwiastek).

Etap 2

Bardziej dokładne wyznaczenie poszukiwanego pierwiastka. Stopień 
dokładności określony jest przez zadany, dopuszczalny błąd. 

 

Krzysztof Pancerz

Algorytmy i struktury danych

Metoda bisekcji 

(połowienia przedziału, równego podziału)

Dane jest równanie f(x)=0.

Zakładamy, że:

●

 funkcja f jest ciągła w przedziale domkniętym [a,b],

●

 wewnątrz przedziału [a,b] znajduje się dokładnie jeden pierwiastek,

●

 zachodzi nierówność f(a)f(b)<0.

Kolejne (w i-tym kroku) przybliżenie pierwiastka obliczamy ze wzoru: 

x

i

=

a

i

b

i

2

 

Krzysztof Pancerz

Algorytmy i struktury danych

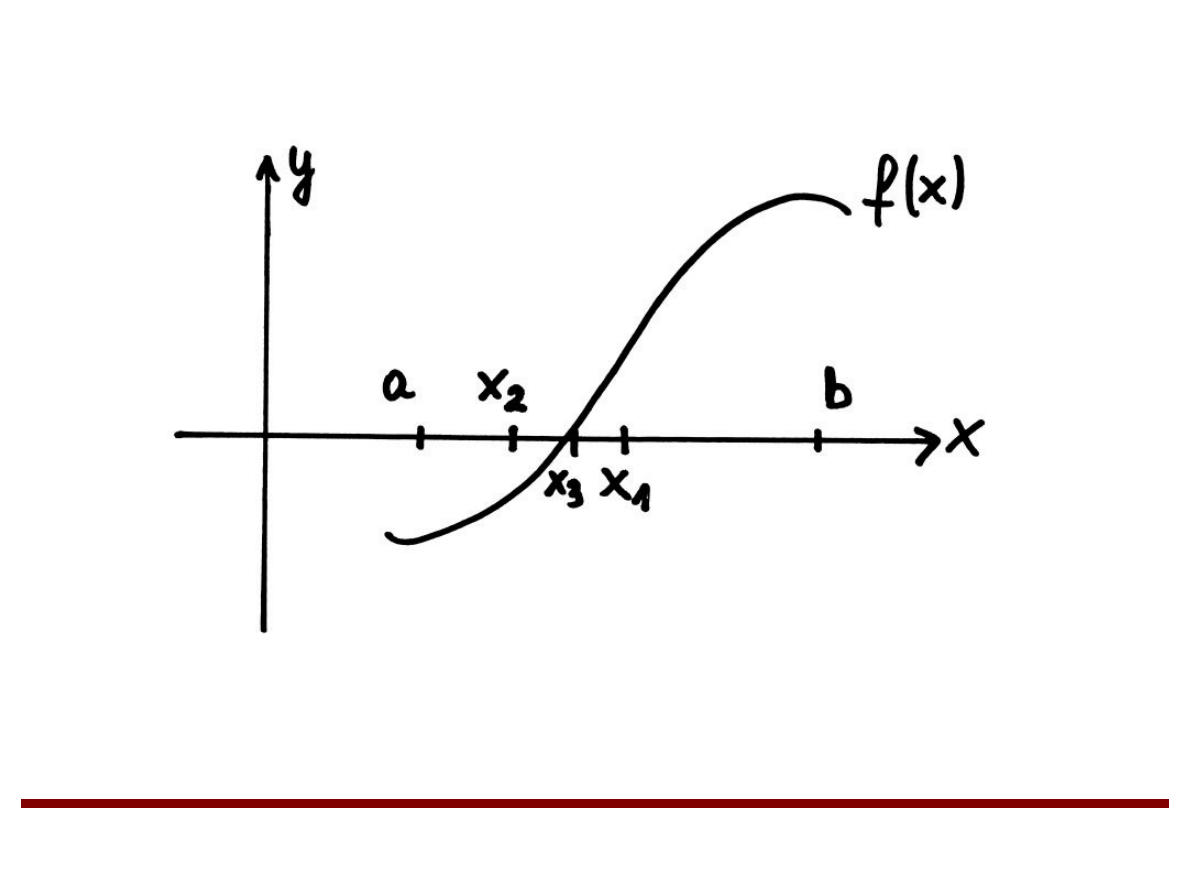
Metoda bisekcji 

x1 – pierwsze przybliżenie pierwiastka
x2 – drugie przybliżenie pierwiastka
x3 – trzecie przybliżenie pierwiastka
...

 

Krzysztof Pancerz

Algorytmy i struktury danych

Metoda bisekcji 

(połowienia przedziału, równego podziału)

wczytaj(a,b,e)
x←a
dopóki ( |f(x)|>e ) wykonuj
{

x←(a+b)/2
jeśli( znak(f(a)) ≠ znak(f(x)) ) wykonaj 
{ b←x }
w przeciwnym razie
{ a←x }

}
wypisz (x)

a,b – końce przedziału, w którym poszukujemy pierwiastka
e – dopuszczalny błąd znalezienia pierwiastka
f – dana funkcja nieliniowa

 

 

Krzysztof Pancerz

Algorytmy i struktury danych

Metoda siecznych 

(regula falsi)

Dane jest równanie f(x)=0.

Zakładamy, że:

●

 funkcja f jest ciągła w przedziale domkniętym [a,b],

●

 wewnątrz przedziału [a,b] znajduje się dokładnie jeden pierwiastek,

●

 zachodzi nierówność f(a)f(b)<0. 

Kolejne (w i-tym kroku) przybliżenie pierwiastka obliczamy ze wzoru: 

x

i

=a

i

−

b

i

−a

i

 f a

i



f

b

i

− f a

i



 

Krzysztof Pancerz

Algorytmy i struktury danych

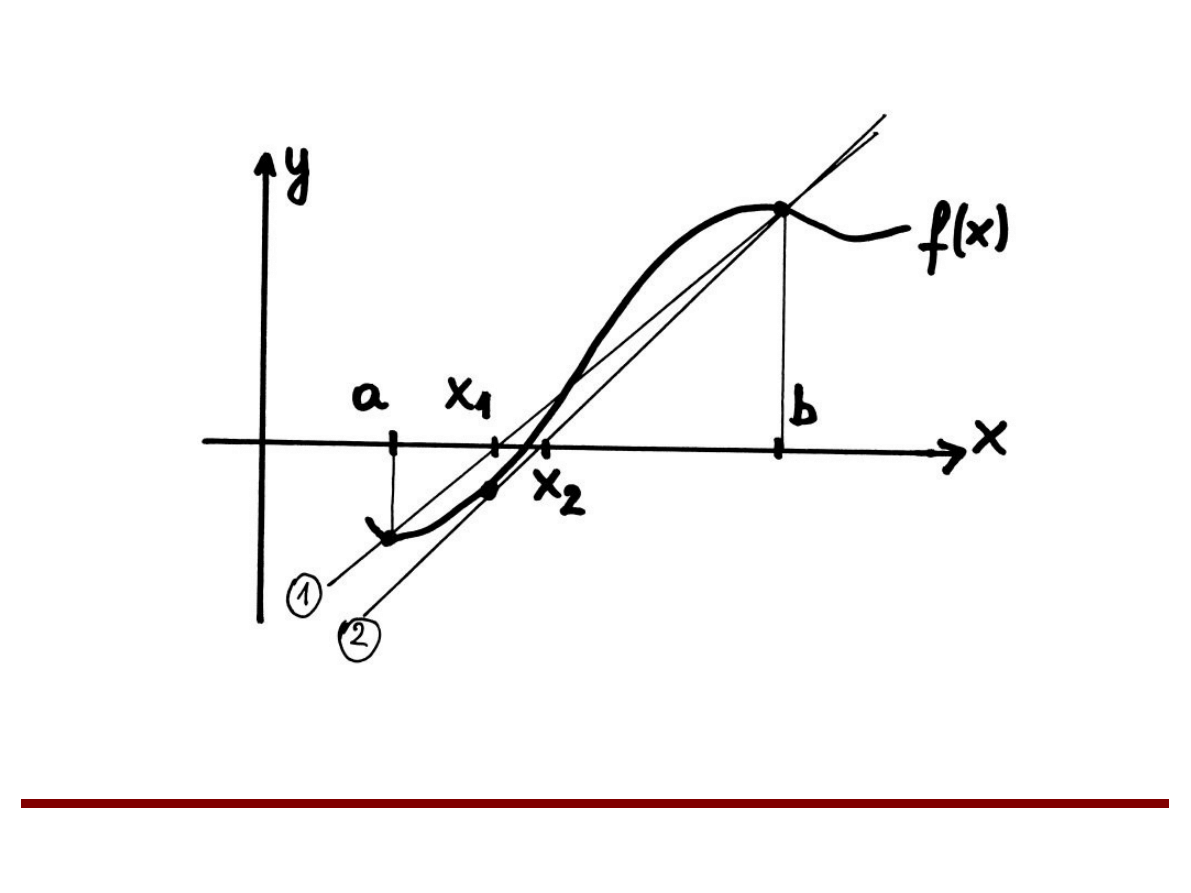
Metoda siecznych 

x1 – pierwsze przybliżenie pierwiastka
x2 – drugie przybliżenie pierwiastka
...

 

Krzysztof Pancerz

Algorytmy i struktury danych

Metoda siecznych

wczytaj(a,b,e)
x←a
dopóki ( |f(x)|>e ) wykonuj
{

x←a-( (b-a)f(a)/(f(b)-f(a)) )
jeśli( znak(f(a)) ≠ znak(f(x)) ) wykonaj
{ b←x }
w przeciwnym razie
{ a←x }

}
wypisz (x)

a,b – końce przedziału, w którym poszukujemy pierwiastka
e – dopuszczalny błąd znalezienia pierwiastka
f – dana funkcja nieliniowa

 

 

Krzysztof Pancerz

Algorytmy i struktury danych

Metoda stycznych (Newtona)

Dane jest równanie f(x)=0.

Zakładamy, że:

●

 funkcja f jest ciągła w przedziale domkniętym [a,b],

●

 wewnątrz przedziału [a,b] znajduje się dokładnie jeden pierwiastek,

●

 zachodzi nierówność f(a)f(b)<0. 

Kolejne (w i-tym kroku) przybliżenie pierwiastka obliczamy ze wzoru: 

x

i

=a

i

−

f

a

i



f '

a

i



 

Krzysztof Pancerz

Algorytmy i struktury danych

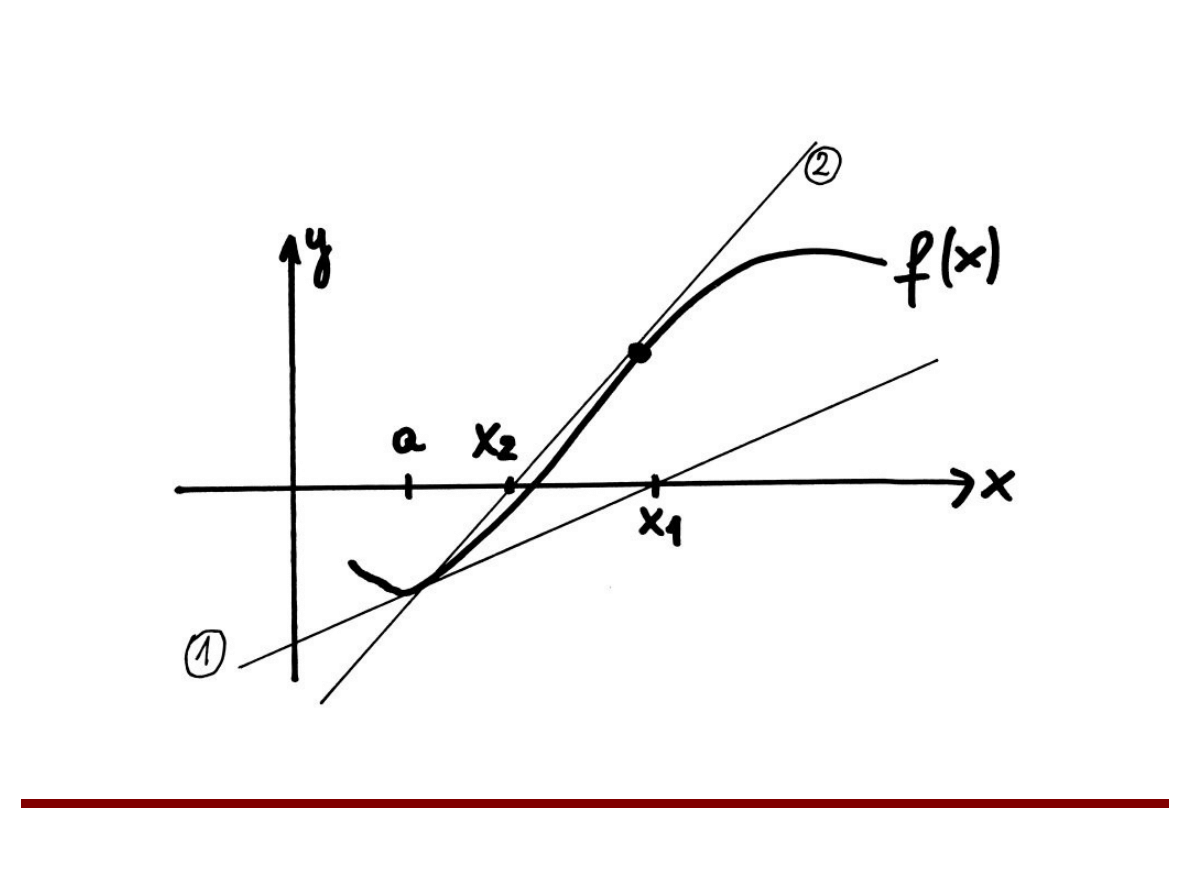
Metoda stycznych

x1 – pierwsze przybliżenie pierwiastka
x2 – drugie przybliżenie pierwiastka
...

 

Krzysztof Pancerz

Algorytmy i struktury danych

Metoda stycznych (Newtona)

wczytaj(a,e)
x←a
dopóki ( |f(x)|>e ) wykonuj
{

x←a-(f(a)/f'(a))
a←x

}
wypisz (x)

a – punkt startowy, od którego zaczynamy poszukiwanie pierwiastka
e – dopuszczalny błąd znalezienia pierwiastka
f – dana funkcja nieliniowa

 

 

Krzysztof Pancerz

Algorytmy i struktury danych

Porównanie metod

Metoda bisekcji
ZALETA: - przy spełnionych założeniach wstępnych metoda zawsze 
prowadzi do rozwiązania
WADA: -metoda nieefektywna (zbieżność metody jest bardzo wolna, 
szybkość zbieżności zupełnie nie zależy od funkcji f)

Metoda siecznych
ZALETA: - przy spełnionych założeniach wstępnych metoda zawsze 
prowadzi do rozwiązania
WADA: - powolna zbieżność metody

Metoda stycznych
ZALETA: - metoda najszybciej zbieżna
WADY: - metoda wymaga obliczania wartości pochodnej
- zbieżność metody zależy od wyboru punktu startowego (dla pewnych 
punktów metoda może nie być zbieżna)