U N I W E R S Y T E T Ś L Ą S K I

WYDZIAŁ TECHNIKI

Instytut Informatyki

PRACA MAGISTERSKA

Grzegorz Pustelnik

Pakiet programów edukacyjnych z zakresu przedmiotu wprowadzenie do informatyki

Promotor:

Dr Urszula Boryczka

Sosnowiec 1998

Spis treści

Wstęp ............................................................................................................................... 3

I. Zasady automatycznej translacji

1.1 Translacja i translatory ...............................................................................................4

1.2 Stos i odwrotna notacja polska (ONP) .......................................................................6

1.3 Translacja wyrażeń arytmetycznych ..........................................................................6

II Automat skończony

2.1 Deterministyczny automat skończony .................................................................... 15

2.2 Niedeterministyczny automat skończony ............................................................... 22

2.3 Automat skończony z ε-ruchami ............................................................................. 24

2.4 Wyrażenia regularne ................................................................................................ 25

2.5 Zastosowania automatów skończonych .................................................................. 30

III Maszyna Turinga

3.1 Podstawowy model maszyny Turinga ..................................................................... 31

IV Gramatyki bezkontekstowe

4.1 Podstawowe pojęcia gramatyk ................................................................................ 40

4.2 Gramatyki bezkontekstowe ..................................................................................... 44

4.3 Drzewa wyprowadzeń ............................................................................................. 47

V. Opis programów

5.1 ONP ....................................................................................................................... 50

5.2 AS .......................................................................................................................... 55

5.3 MT .......................................................................................................................... 58

5.4 GR .......................................................................................................................... 62

5.5 Zawartość dysku CD-ROM .................................................................................. 64

Literatura ...................................................................................................................... 65

WSTĘP

Praca dydaktyczna „Pakiet programów edukacyjnych z zakresu przedmiotu wprowadzenie do informatyki” zawiera podstawy najogólniej rozumianej teorii automatów leżącej u podstaw informatyki.

Ze względu na rozległość tej dziedziny wiedzy, niniejsza praca przedstawia tylko zagadnienia zgodne z przedmiotem prowadzonym na I roku studiów : Wprowadzenie do informatyki.

Część teoretyczna została napisana po kątem zagadnień poruszanych przez prowadzących ten przedmiot i może stanowić formę skryptu uczelnianego.

Rozdział I dotyczy zasad automatycznej translacji. Opisuje dwustopniową translację wyrażeń arytmetycznych na drodze: wyrażenie arytmetyczne postać ONP , jak również postać ONP język symboliczny. Odwrotna notacja polska (ONP) to jeden z wariantów beznawiasowego zapisu wyrażeń formalnych wynaleziony przez polskiego logika J.Łukasiewicza.

W rozdziale II przedstawiono zagadnienia związane z teorią automatów skończonych, uwypuklając trzy podstawowe rodzaje: DAS- deterministyczny automat skończony, NAS- niedeterministyczny automat skończony i NAS z ε-ruchami oraz języki akceptowane przez automaty - zbiory regularne.

Rozdział III dotyczy maszyny Turinga. Przedstawia podstawowy model maszyny algorytmicznej Alana Turinga, będącej prymitywnym modelem komputera. Przedstawiono w nim także liczne przykłady , które posłużyły do przedstawienia zaskakującej tezy Churcha-Turinga.

W rozdziale IV opisano wybrane zagadnienia z szerokiej teorii języków, skupiając swoją uwagę na gramatykach bezkontekstowych, mających najszersze zastosowania w informatyce.

Część praktyczna- to cztery programy edukacyjne, które odzwierciedlają zagadnienia części teoretycznej.

Dynamiczny rozwój informatyki w ostatnich latach sprawia, że ta dziedzina wiedzy staje się coraz bardziej popularna, stąd warto czasami poznać podstawy teoretyczne i początkowe badania z tego zakresu. Niektóre z nich zawarte są w niniejszej pracy teoretycznej, zaś programy do niej dołączone są pewną propozycją przyswojenia wiadomości, z których można skorzystać u progu tajników informatyki.

I. ZASADY AUTOMATYCZNEJ TRANSLACJI

1.1 Translacja i translatory

Zagadnienia budowy translatorów, jak i samego procesu translacji stanowią jeden z najrozleglejszych działów informatyki, któremu możnaby poświęcić odrębną pracę, toteż niniejsze rozważania mają na celu zaznaczenie pewnych pojęć z tego zakresu, skupiając się głównie na procesie translacji wyrażeń do postaci ONP. Głównym źródłem informacji wykorzystanym dla tego rozdziału jest pozycja: W. M.Turskiego [TURS 77].

Języki programowania niskiego czy też wysokiego poziomu mają na zadanie przetworzyć ogół algorytmów w nich zapisanych na taką postać aby maszyna cyfrowa była w stanie je wykonać tzn. dać takie efekty jakie programista zakłada tworząc dany program. Między tymi językami występuje jednak zasadnicza różnica : program zapisany w języku niskiego poziomu (w języku wewnętrznym) stanowi ciąg instrukcji dostępnych przez dany procesor czy też maszynę cyfrową i jest wykonywany bezpośrednio; natomiast program zapisany w językach wysokiego poziomu takich jak Pascal czy C ( w językach zewnętrznych) wymaga dodatkowo przetłumaczenia na ciąg instrukcji dostępnych przez maszynę która ma dany program wykonać. Owo tłumaczenie w pewnym stopniu przypomina tłumaczenie języków etnicznych, przy uwzględnieniu dodatkowych warunków jak: znajomość kultury, tradycji i historii danego języka. Podobnie tłumacząc programy zewnętrzne na wewnętrzne należy także uwzględnić dodatkowe elementy takie jak dane wejściowe do programu, które także muszą być przetłumaczone do tego stopnia aby spodziewany efekt końcowy programu zapisanego w języku zewnętrznym niczym się nie różnił od efektu działania samej maszyny.

Proces przekładu tekstów zapisanych w jednym języku na drugi nosi nazwę translacji. W przypadku gdy dany język wysokiego poziomu ma stosunkowo łatwą gramatykę, translacja może być wykonana samoczynnie przez maszynę cyfrową przy pomocy specjalnego programu translacji zwanego translatorem.

Wykorzystując translatory programiści mogą posługiwać się zewnętrznymi językami programowania, co znacznie ułatwia tworzenie oprogramowania, gdyż czas stracony na żmudnym pisaniu instrukcji w języku wewnętrznym zostaje ograniczony do wybrania odpowiednich procedur i funkcji z repertuaru danego języka wysokiego poziomu, a sam programista może skupić się na rozwiązywaniu powstałych problemów implementacyjnych.

Translatory dzielimy zazwyczaj na dwie kategorie: kompilatory i interpretatory. Podział ten bardzo często nie ma miejsca w praktyce, gdyż buduje się translatory wykazujące jednocześnie cechy kompilatorów i interpretatorów.

Najogólniej, kompilator jest translatorem, operującym na całym tekście programu źródłowego generując tekst przekładu jako całość, podczas gdy interpreter operuje na poszczególnych jednostkach syntaktycznych programu źródłowego i generuje ich przekłady. Jeśli więc wykonywamy program początkowo zapisany w języku zewnętrznym to:

-używając kompilatora, możemy przystąpić do wykonania programu w postaci docelowej dopiero po zakończeniu translacji. Oznacza to, że uzyskany tekst będący przekładem tekstu źródłowego w całości wprowadzany jest do maszyny cyfrowej;

-używając interpretatora, możemy wykonywać przekłady poszczególnych jednostek syntaktycznych, nie czekając na cały proces translacji. Oznacza to, że cały czas operujemy na tekście źródłowym tłumacząc tylko te jednostki syntaktyczne, które są potrzebne aby poszczególny fragment programu mógł zadziałać.

W praktyce rzadko dokonuje się bezpośredniej translacji programów z języka zewnętrznego na język maszynowy. Najczęściej stosuje się proces pośredni to znaczy, najpierw dokonuje się translacji z języka zewnętrznego na język asemblerowy, a potem z języka asemblerowego na język maszynowy. Zastosowanie takiej dwuetapowej translacji niesie za sobą wiele zalet, a główna z nich jest możliwość łączenia poszczególnych części programów zapisanych w różnych językach zewnętrznych.

1.2 Stos i odwrotna notacja polska (ONP)

Bardzo ważnymi pojęciami bez których trudne byłoby zrozumienie zasad jakiejkolwiek translacji są : stos i odwrotna notacja polska (ONP).

STOS- jest to organizacja sekwencyjna pamięci operacyjnej maszyny cyfrowej. Stos działa jak pojemnik określonych jednostek, przy czym pobieranie elementów w nim zgromadzonych odbywa się w kolejności odwrotnej do magazynowania. Jest to tak zwana struktura LIFO (last-in-first-out co oznacza „ ten co ostatni przyszedł pierwszy odchodzi”). Dla stosu określa się dwie podstawowe operacje:

• dos(a)- dopisz na stosie - w wyniku wykonania tej operacji jednostka a zostaje umieszczona na szczycie stosu (staje się pierwszym elementem stosu)

• ods(a)- odczytaj ze stosu - w wyniku wykonania tej operacji jednostka a zostaje wydana na zewnątrz stosu.

ODWROTNA NOTACJA POLSKA (ONP)- mianem tym obdarzono jeden z wariantów beznawiasowego zapisu wyrażeń formalnych, wynalezionego przez polskiego logika Jana Łukasiewicza (1878-1956). W tym beznawiasowym zapisie symbole operandów poprzedzają bezpośrednio symbol operatora, na przykład wyrażenie a+b zapisujemy w ONP jako a b +.

1.3 Translacja wyrażeń arytmetycznych

Współczesne podejście translacji wyrażeń arytmetycznych polega na wydzieleniu dwu etapów translacji:

- translacja do ONP

- translacja ONP na język symboliczny

W celu zobrazowania translacji do ONP przyjmujemy, że źródłowy zapis wyrażeń arytmetycznych pojawia się na wejściu specjalnego automatu (Rys.1). Na wyjściu uzyskamy zapis ONP tych wyrażeń, sam zaś automat wyposażony jest w pamięć stosową.:

wyrażenie Automat ze stosem ONP wyrażenia

arytmetyczne arytmetycznego

Rys. 1. Model automatu ze stosem do translacji wyrażeń arytmetycznych

Podczas translacji wyrażeń arytmetycznych szczególnej analizie poddawane są symbole operacji (+,-,*,itp.) zwane ogranicznikami ,stąd wprowadza się dodatkowo listę priorytetów ograniczników (Tab.1):

Ogranicznik	Priorytet
+ -	0
* / ÷	1
↑	2

Tab.1.Priorytety symbolów operacji (ograniczników)

Działanie automatu odbywa się według następującego algorytmu postępowania:

1. Pobierz kolejny element (nazwę zmiennej, stałą lub ogranicznik) źródłowego wyrażenia arytmetycznego.

2. Jeśli ten element jest nazwą zmiennej lub stałą, przekaż go natychmiast na wyjście; w przeciwnym wypadku, jeśli priorytet ogranicznika jest wyższy od priorytetu ogranicznika zajmującego szczyt stosu lub jeśli stos jest pusty, dopisz go na stos, jeśli wreszcie na szczycie stosu znajduje się ogranicznik o wyższym lub równym priorytecie - odczytaj go ze stosu i prześlij na wyjście, a ogranicznik z wejścia dopisz na stosie, chyba, że nowy ogranicznik zajmujący szczyt stosu w wyniku odczytania priorytetu ma priorytet nie mniejszy niż ogranicznik z wejścia. w takim przypadku należy kontynuować odczytywanie ze stosu i przesyłanie na wyjście aż do wystąpienia na szczycie stosu ogranicznika o priorytecie niższym od priorytetu ogranicznika nadchodzącego z wejścia.

3. Jeśli wyrażenie źródłowe zostało wyczerpane, odczytaj wszystkie ograniczniki ze stosu na wyjście automatu.

Przykład 1 przedstawia poszczególne takty procesu translacji do ONP dla wybranego wyrażenia arytmetycznego.

Przykład 1:

Niech wyrażenie źródłowe ma postać: x + 3 * z ÷ k

Poszczególne takty translacji są następujące:

Takt	Wejście	Stos	Wyjście
1	x		x
2	+	+
3	3	+	3
4	*	+,*
5	z	+,*	z
6	÷	+,÷	*
7	k	+,÷	k
8	koniec		÷,+

Rys.2. Poszczególne takty procesu translacji wyrażenia do ONP dla przykładu 1

Na wyjściu uzyskamy wyrażenie ONP postaci: x, 3, z, *, k, ÷, +

Dla uzyskania prawidłowej konwersji wyrażeń arytmetycznych uzupełniamy listę ograniczników o następujące symbole:

• nawiasy ( )

• operator negacji NEG (jako symbol operacji unarnej służący do zmiany znaku)

• funkcje trygonometryczne (operatory jednoargumentowe)

Priorytety wyżej wymienionych ograniczników przedstawia tabela 2

Ogranicznik	Priorytet
(	0
+ - )	1
* / ÷ NEG	2
↑	3
sin cos tg ctg	4

Tab.2. Priorytety rozszerzonych symbolów operacji (ograniczników)

Działanie automatu uzupełniamy następującymi regułami:

1. Ogranicznik „(” jest dopisywany do stosu bez jakiegokolwiek odczytywania stosu.

2. Ogranicznik „)” nie jest dopisywany na stos, pojawienie się jednak tego ogranicznika na wejściu powoduje odczytanie ze stosu i przesłanie na wyjście wszystkich kolejnych ograniczników aż do pojawienia się ogranicznika „(”.

3. Ogranicznik „(” ze szczytu stosu zostaje usunięty bez przekazywania na wyjście, jeśli aktualnym symbolem na wejściu jest „)”.

Pojawienie się nawiasu zamykającego „)” na wejściu automatu powoduje wyprowadzenie na wejście wszystkich ograniczników z wnętrza pary nawiasów aż do nawiasu otwierającego „(” oraz likwidację tego nawiasu.

Przykład 2 przedstawia proces translacji z uwzględnieniem powyższych reguł:

Przykład 2:

Niech wyrażenie źródłowe ma postać: b * c ↑ ( d - e*k )

Poszczególne takty translacji są następujące:

Takt	Wejście	Stos	Wyjście
1	b		b
2	*	*
3	c	*	c
4	↑	*,↑
5	(	*,↑,(
6	d	*,↑,(	d
7	-	*,↑,(,-
8	e	*,↑,(,-	e
9	*	*,↑,(,-,*
10	k	*,↑,(,-,*	k
11	)	*,↑	*,-
12	koniec		↑,*

Rys.3. Poszczególne takty procesu translacji wyrażenia do ONP dla przykładu 2

Na wyjściu uzyskamy wyrażenie ONP postaci: b, c, d, e, k, *, -, ↑ ,*

Przykład 3 przedstawia translację krótkiego wyrażenia arytmetycznego z funkcjami trygonometrycznymi.

Przykład 3:

Niech wyrażenie źródłowe ma postać: sinx + cosy + tgz

Poszczególne takty translacji są następujące:

Takt	Wejście	Stos	Wyjście
1	sin	sin
2	x	sin	x
3	+	+	sin
4	cos	+, cos
5	y	+, cos	y
6	+	+	cos, +
7	tg	+, tg
8	z	+, tg	z
9	koniec		tg, +

Rys.4. Poszczególne takty procesu translacji wyrażenia do ONP dla przykładu 3

Na wyjściu uzyskamy wyrażenie ONP postaci: x , sin, y, cos, +, z, tg, + ,

Nic nie stoi na przeszkodzie by procesowi translacji poddać wyrażenia arytmetyczne zawierające operacje logiczne i warunkowe. W tym celu należy odpowiednio rozszerzyć ilość priorytetów, a także chcąc odzwierciedlić składnie: if..then..else należy wprowadzić odpowiednie oznaczenia, które będą sygnalizowały konieczność wykonania skoku warunkowego lub bezwarunkowego. Operacje te zapisujemy w postaci SW (k) i SB (k), gdzie SW- oznacza then, a SB else. Dla translacji wyrażeń arytmetycznych z elementami logicznymi koniecznym jest wprowadzenie dwóch różnych pojęć priorytetów: priorytet porównawczy (p.p) i priorytet stosowy (p.s.). gdzie: priorytet porównawczy dla danego ogranicznika oznacza moc rozładowania stosu, a priorytet stosowy moc blokowania stosu. W praktyce oznacza to, że jeżeli na wejściu automatu pojawi się symbol operacji (ogranicznik) to celem ewentualnego odczytania symboli ze stosu porównujemy priorytet porównawczy tego symbolu z priorytetem stosowym symboli operacji na stosie.

Uzupełniona tablica priorytetów ograniczników wraz z uwzględnieniem pojęć: priorytet stosowy i porównawczy kształtuje się następująco:

Ogranicznik	p. stosowy	p. porównawczy
(, if	0	nie dotyczy
then	0	1
else	1	2
), ;	nie dotyczy	1
≡	3	3
⊃	4	4
∧	5	5
∨	6	6
-	7	7
> ≥ ≤ < = ≠	8	8
+-	9	9
* / ÷NEG	10	10
↑	11	11

Tab.3. Uzupełniona lista ograniczników z uwzględnieniem elementów logicznych

Algorytm konwersji zostaje uzupełniony o nowe reguły związane z elementami logicznymi: if..then...else:

1. Gdy na wejściu pojawi się ogranicznik „then”, wówczas, oprócz wszystkich ograniczników wyprowadzanych ze stosu na wyjście ze względu na ich priorytety, zostaje także usunięty ze szczytu stosu ogranicznik „if” ( konstrukcja if - then jest analogiczna do pary nawiasów ( ) w wyrażeniach arytmetycznych). Na wyjście automatu zostaje wyprowadzona operacja SW z pustym nawiasem SW( ), zaś ogranicznik „then” zostaje dopisany do stosu wraz z numerem, pod jakim występuje w zapisie ONP operacja SW( ).

2. Gdy na wejściu pojawia się ogranicznik „else”, powoduje on wyprowadzenie wszystkich symboli na wyjście automatu aż do momentu pojawienia się ma stosie ogranicznika „then”. Na wyjście zostaje wpisana niekompletna operacja SB(), operacja SW( ) będąca na wyjściu zostaje uzupełniona przez wpisanie do nawiasu numeru pozycyjnego z zapisu ONP, a sam ogranicznik „else” zostaje dopisany do stosu wraz z numerem pozycyjnym SB( ) w zapisie ONP.

3. Gdy podczas wyprowadzania ograniczników ze stosu natrafimy na „else”, wówczas uzupełniamy odpowiedni nawias operacji SB( ) odpowiadającej danemu „else”, zaś sam ogranicznik else zostaje zlikwidowany tzn. nie jest wyprowadzany na wyjście automatu.

Przykład 4 obrazuje translację wyrażeń zawierających elementy logiczne.

Przykład 4:

Niech wyrażenie na wejściu ma postać: y + ( if a>0 then 3 else a )

Poszczególne takty konwersji przedstawia rysunek 5.

Takt	Wejście	Stos	Wyjście	Numer pozycyjny w ONP
1	y		y	1
2	+9	+9
3	(	+9 (0
4	if	+9 (0 if0
5	a	+9 (0 if0	a	2
6	>8	+9 (0 if0 >8
7	0	+9 (0 if0 >8	0	3
8	then1	+9 (0 then^50	> SW() po takcie 10 - SW(8)	4 5
9	3	+9 (0 then^50	3	6
10	else2	+9 (0 else^71	SB() po takcie 12- SB(9)	7
11	a	+9 (0 else^71	a	8
12	)1	+9
13	;		+	9

Górne indeksy przy then i else oznaczają numer pozycyjny instrukcji SW i SB w ONP, zaś indeksy dolne oznaczają priorytet stosowy lub porównawczy danego ogranicznika.

Rys.5. Poszczególne takty konwersji dla przykładu 4

Etap drugi translacji wyrażeń arytmetycznych polega na wygenerowaniu programu w języku symbolicznym (docelowym). Proces ten także korzysta z pamięci stosowej a sam algorytm postępowania wymaga przyjęcia pewnych oznaczeń :

δ_i - i=0,1,.... są to kolejne pozycje stosu; język docelowy pozwala na występowanie dwu typów instrukcji: δ_i := Z i δ_i : = δ_i op δ_i+1 gdzie Z jest nazwą zmiennej lub stałą, a op jest symbolem operacji.

Proces translacji zapisu ONP na język docelowy przebiega według następującego algorytmu:

1. Ustalamy i=0, k=1

2. Odczytujemy k-ty element ONP : E_k

3. Jeśli E_k jest nazwą zmiennej lub stała, generuje się operacja δ_i:=E_k i następuje zwiększenie i o 1 → i:= i +1; jeśli E_k jest symbolem operacji op ≠ NEG, generuje się operacja δ_i-2 := δ_i-2 op δ_i-1 oraz następuje zmniejszenie i o 1 → i := i - 1; jeśli E_k = NEG, następuje wygenerowanie operacji δ_i-1 := - δ_i-1

4. Jeśli E_k nie był ostatnim symbolem wyrażenia w ONP, to k:= k + 1 i przechodzimy do punktu 2.

Sposób translacji wyrażenia ONP na język symboliczny przedstawia przykład 5.

Przykład 5:

Niech wyrażenie arytmetyczne ma postać: ( a + b ) / ( k ↑ (-c) )

Postać ONP tego wyrażenia jest następująca: a, b, +, k, c, NEG, ↑ /

i k

0 1

1: δ₀:= a 1 2

2: δ_i:= b 2 3

3: δ₀:= δ₀ +δ_i 1 4

4: δ_i:= k 2 5

5: δ₂:= c 3 6

6: δ₂:= -δ₂ 3 7

7: δ_i:= δ_i ↑ δ₂ 2 8

8: δ₀:= δ_o / δ₁ 1 9

9: brak symboli w wyrażeniu ONP -koniec algorytmu.

Wiadomości zawarte w tym rozdziale przedstawiają nam drogę od zrodzenia się algorytmu, aż po wykonanie programu na maszynie cyfrowej co schematycznie przestawia rysunek 6

algorytm programowanie program w języku

wysokiego poziomu

kod maszynowy program w języku kompilacja

asemblerowym

Wykonanie na

komputerze

Rys.6. Schematyczny przebieg powstania programu

II. AUTOMAT SKOŃCZONY

2.1 Deterministyczny automat skończony

W tym rozdziale tematem rozważań będą zagadnienia z dziedziny automatów skończonych i wyrażeń regularnych. Głównym źródłem wiadomości teoretycznych przedstawionych w tym rozdziale jest praca J.E.Hopcrofta i J.D.Ullmana [HOPC 94].

Automat skończony jest modelem matematycznym systemu o dyskretnych wejściach i wyjściach. System taki w danej chwili może znajdować się w jednym ze skończonej liczby stanów, który to stan jest ściśle uzależniony od stanu poprzedniego. Jeden ze stanów pełni rolę stanu początkowego, od którego dany automat rozpoczyna działanie, z drugiej strony niektóre stany pełnią rolę stanów końcowych kończąc pracę automatu. Praca automatu oparta jest na analizie symboli wejściowych ze skończonego alfabetu. Każdy odczytany symbol wymusza przejście do innego stanu ( w niektórych przypadkach przejście prowadzi do tego samego stanu). Po przeanalizowaniu wszystkich symboli automat skończony może przyjąć jeden z dwu stanów: akceptacji lub nieakceptacji. Bardzo często automat skończony, który w dalszych rozważaniach będziemy oznaczać jako AS jest przedstawiany za pomocą grafów skierowanych, w których wierzchołki obrazują stany automatu. Jeżeli istnieje przejście z jednego stanu do następnego to takie przejście przedstawione jest za pomocą łuku. Dla wyodrębnienia stanu początkowego, wierzchołek rozpoczynający pracę automatu wzbogacony jest o strzałkę z napisem START. W celu zaakcentowania stanu końcowego wprowadza się dwa odrębne wierzchołki grafu opatrzone etykietą A (s. akceptacji) N (s. nieakceptacji), bądź stan końcowy oznacza się podwójnym kółkiem. Rysunek 7 przedstawia fragment grafu dla automatu skończonego:

start q₀ q₁ q₄

q₂ q₃

Rys. 7. Fragment grafu przejść dla automatu skończonego

Automat skończony przedstawiamy formalnie jako uporządkowaną piątkę:

< Q, Σ, δ, q_o, F>

gdzie:

Q - jest skończonym zbiorem stanów,

Σ - jest skończonym alfabetem symboli wejściowych, q₀ należące do Q jest stanem początkowym od którego automat rozpoczyna działanie,

F⊆ Q - jest zbiorem stanów końcowych (stan akceptacji lub nieakceptacji),

δ - jest funkcją odwzorowującą Q x Σ w Q czyli δ określa każdemu stanowi q i każdemu symbolowi na wejściu nowy stan automatu.

Automat skończony możemy sobie wyobrazić jako głowicę sterująco-czytającą, która analizuje symbole zapisane na taśmie w sposób pokazany na rysunku 8.

głowica

sterująco-

czytająca

Rys. 8. Schemat pracy automatu skończonego

W danej chwili automat odczytuje symbol wejściowy i przechodzi do kolejnego stanu. Jeżeli stan ten jest stanem akceptacji to znaczy, że dotychczasowy ciąg symboli na taśmie jest zaakceptowany przez AS. Jeżeli głowica przesunęła się na koniec taśmy, a ostatni stan jest stanem zaakceptowanym przez AS to AS zaakceptował cały łańcuch.

Formalnie przyjmuje się, że łańcuch jest akceptowany przez automat M, jeżeli δ (q_o,x)= p dla jakiegoś p należącego do F. Język akceptowany przez dany automat M oznaczany L(M), to zbiór {x | (q_o,x) należy do F}. Język nazywamy zbiorem regularnym, jeżeli jest on językiem akceptowanym przez pewien automat skończony. Zbiory regularne zostaną szczegółowo omówione pod koniec tego rozdziału.

W celu zobrazowania konstrukcji automatu skończonego przeanalizujmy dwa przykłady dotyczące akceptacji liczb podzielnych przez wybraną liczbę.

Przykład 6. Automat skończony akceptujący liczby podzielne przez 2

Dla tego automatu zbiór symboli wejściowych będzie złożony z cyfr od 0..9 czyli Σ= {0,1,2,3,4,5,6,7,8,9}. Wiadomo też, że liczba jest parzysta gdy ostatnia jej cyfra jest podzielna bez reszty przez 2.

• Konstrukcję automatu rozpoczynamy od wykreślenia wierzchołka stanu q₀, który jest stanem wejściowym (Rys. 8 )

• Jeżeli pojawi się na wejściu cyfra podzielna przez 2 to zaznaczmy to na grafie jako przejście do stanu q₁, jeżeli pojawi się na wejściu cyfra niepodzielna przez 2 to zaznaczmy to jako przejście do stanu q₂ (Rys.9)

• jeżeli AS jest w stanie q₁ i kolejna cyfra na wejściu jest podzielna przez dwa to automat pozostaje nadal w tym samym stanie co zaznaczamy na grafie łukiem wychodzącym z stanu q₁ opatrzonego etykietą {0,2,4,6,8}, jeżeli pozostając w stanie q₂ AS odczyta wszystkie symbole (co umownie oznaczamy pojawieniem się symbolu φ lub # ) wówczas AS przechodzi do stanu akceptacji A (Rys 10)

• jeżeli AS jest w stanie q₁ i kolejna cyfra na wejściu jest nieparzysta to AS pozostaje nadal w tym samym stanie co zaznaczamy na grafie łukiem wychodzącym i wchodzącym do stanu q₂ opatrzonego etykietą {1,3,5,7,9}, jeżeli pozostając w stanie q₂ AS odczyta wszystkie symbole to wówczas AS przechodzi do stanu nieakceptacji N (Rys. 11 )

• Oczywiście istnieje możliwość pojawienia się na wejściu przemiennie liczb parzystych i nieparzystych a tym samym przejścia z stanu q₁ do stanu q₂ (Rys 12 - ostateczna konstrukcja automatu )

start q₀

Rys. 8

{0,2,4,6,8} q₁

start q₀

{1,3,5,7,9} q₂

Rys. 9

{0,2,4,6,8}

φ A

{0,2,4,6,8} q₁

start q₀

{1,3,5,7,9} q₂

Rys. 10

{0,2,4,6,8}

φ A

{0,2,4,6,8} q₁

start q₀

{1,3,5,7,9} q₂ φ

N

{1,3,5,7,9}

Rys.11

{0,2,4,6,8}

φ A

{0,2,4,6,8} q₁

start q_{0 { 1,3,5,7,9} { 0, 2,4,6,8}}

{1,3,5,7,9} q₂ φ

N

{1,3,5,7,9}

Rys. 8-12. Konstrukcja automatu skończonego akceptującego liczby podzielne przez 2

Pojawienie się na wejściu liczby np.123 dla rozpatrywanego automatu sprawi, że automat przejdzie przez następujący porządek stanów: q₀, q₂, q₁, q₂, N - czyli liczba 123 nie zostanie zaakceptowana przez automat ( co jest zgodne z prawda gdyż 123 nie jest liczbą parzystą); natomiast pojawienie się liczby 36 wymusi przejście przez stany: q₀, q₂, q₁, A-czyli liczba zostanie zaakceptowana prze automat (co jest zgodne z prawdą gdyż 36 - jest liczbą parzystą).

Przykład 7. Automat skończony akceptujący liczby podzielne przez 3.

Dla tego automatu zbiór symboli wejściowych będzie złożony z cyfr od 0..9 czyli Σ= {0,1,2,3,4,5,6,7,8,9}. Wiadomo też, że liczba jest podzielna bez reszty przez 3 gdy suma cyfr danej liczby jest podzielna przez 3. Musimy więc rozpatrzyć następujące przypadki tego zadania: po pierwsze jeżeli liczba złożona jest z cyfr 0,3,6,9 to jest ona na pewno podzielna przez 3. Dla cyfr 1,4,7 i 2,5,8 rozpatrza się dodatkowe warunki : pojawienie się cyfr 1,4,7 musi wystąpić trzykrotnie bądź musi wystąpić cyfra 2,5,8 by liczba była podzielna przez 3. Tak samo pojawienie się cyfr 2,5,8 musi wystąpić trzykrotnie bądź po pojawieniu się jednej z nich musi wystąpić cyfra 1,4,7. Diagram przejść takiego automatu przedstawia rysunek 13.

{0,3,6,9}

φ

q₁ N

{1,4,7}

{0,3,6,9}

{2,5,8}

q_o {1,4,7} {2,5,8}

Start {2,5,8}

φ

A {1,4,7} φ

q₂ N

{0,3,6,9}

Rys. 13. Automat skończony akceptujący liczby podzielne przez 3

Pojawienie się na wejściu liczby 126 spowoduje przejście automatu przez stany: q₀, q₁, q₂, A czyli cyfra jest podzielna przez trzy, natomiast 125 wymusi drogę: q₀, q₁, q₂, N czyli liczba nie jest podzielna przez 3.

W praktyce badanie czy dana liczba jest podzielna przez n sprowadza się do operacji modulo (badanie reszty z dzielenia liczby przez n). W tym celu przed wykreśleniem grafu automatu skończonego tworzymy tabelę stanów, obrazującą przejścia między stanami w zależności od rozpatrywanej cyfry. Tabelę taką tworzymy w następujący sposób:

• liczba kolumn jest równa n, czyli liczbie przez którą dana liczba wejściowa ma być podzielna,

• natomiast liczba wierszy jest równa liczbie cyfr (0-9) uzupełniona o 1 dla symbolu pustego φ.

Przeanalizujmy tabelę 4, która dotyczy automatu skończonego badającego czy liczba jest podzielna przez 3.

	q1	q2	q3
φ	T	N	N
0	q1	q2	q3
1	q2	q3	q1
2	q3	q1	q2
3	q1	q2	q3
4	q2	q3	q1
5	q3	q1	q2
6	q1	q2	q3
7	q2	q3	q1
8	q3	q1	q2
9	q1	q2	q3

Tab.4.Tabela stanów dla automatu skończonego akceptującego liczby podzielne przez 3

Chcąc stworzyć automat skończony badający podzielność liczb przez 4, do tabeli 4 dodajemy jedną kolumnę z stanem q4, zaś samo liczenie w pionie zwiększamy do 4, czyli pierwsza kolumna będzie miała następujący porządek stanów: q1, q2, q3, q4, q1, q2, q3, q4, q1, q2. Na tej podstawie możemy stworzyć automat badający podzielność przez dowolną liczbę.

Dla tego typu automatów pojawienie się na wejściu jakiegokolwiek symbolu powoduje ruch automatu ściśle określoną drogą bez możliwości wyboru. Jak się okaże w kolejnych podrozdziałach wybór drogi automatu wcale nie musi być z góry określony tzn. że dany symbol wejściowy może wymusić przejście do różnych stanów. Dlatego automaty skończone gdzie istnieje tylko jedna droga przejścia ze stanu do stanu dla danego symbolu wejściowego określa się jako deterministyczne automaty skończone (DAS).

2.2 Niedeterministyczny automat skończony

Jak już zostało wspomniane w końcówce poprzedniego podrozdziału dany symbol wejściowy może wymusić przejście do różnych stanów, stąd wprowadźmy modyfikację modelu automatu skończonego, polegającą na istnieniu kilku przejść ze stanu przy tym samym symbolu wejściowym. Taka modyfikacja pozwala zdefiniować model niedeterministycznego automatu skończonego (NAS), który formalnie jest definiowany jako uporządkowana piątka:

<Q, Σ, δ, q_o, F>

gdzie:

Q - jest skończonym zbiorem stanów,

Σ - jest skończonym alfabetem symboli wejściowych, q₀ należące do Q jest stanem początkowym od którego automat rozpoczyna działanie,

F⊆ Q - jest zbiorem stanów końcowych (stan akceptacji lub nieakceptacji),

δ- jest odwzorowaniem Q x Σ w 2^Q. (2^Q - jest zbiorem potęgowym Q, czyli zbiorem wszystkich podzbiorów Q), czyli δ (q,a) jest zbiorem wszystkich stanów p, dla których istnieje przejście ze stanu q do p o etykiecie związanej z symbolem wejściowym a.

Rysunek 14 przedstawia konstrukcję NAS akceptującego ciągi zerojedynkowe w których przynajmniej raz wystąpiło podwojenie zer lub jedynek:

^{1 1}

₀ 0 0 ⁰

start q₀ q₃ q₄

1

q₁

1

q₂

⁰

¹

Rys.14. Niedeterministyczny automat skończony akceptujący ciągi, w których wystąpiło podwojenie zer lub jedynek.

Z rysunku 14 widać, że ze stanu q₀ wychodzą dwie krawędzie (drogi) o etykiecie 0, czyli z chwilą pojawienia się zera na wejściu istnieje możliwość przejścia ze stanu q₀ do stanu q₁ lub q₃ . Taka właśnie możliwość wyboru stanów przy tym samym symbolu wejściowym wyróżnia NAS od DAS. Ten typ automatów będzie akceptował ciąg symboli a₁,a₂...a_n, dla którego istnieje ciąg przejść prowadzący od stanu początkowego do stanu końcowego. Dla przykładu ciąg 101001 zostanie zaakceptowany przez powyższy NAS bo istnieje towarzyszący mu ciąg przejść: q₀, q₀, q₀, q₃, q₄, q₄; natomiast dla ciągu 10101 nie istnieje żadne przejście ze stanu początkowego do końcowego, gdyż automat w wyniku pojawienia się symboli 10101 pozostanie w stanie q₀ czyli wyrażenie nie zostanie zaakceptowane.

Rysunek 15 przedstawia jeszcze jeden niedeterministyczny automat skończony, który akceptuje ciągi wyrazowe w których wystąpiła przynajmniej raz sekwencja symboli a b c.

{ dowolny symbol }

{ dowolny symbol }

{ w tym a i b } b c

q₁ q₂ q₃

a

Start q₀

Rys. 15. NAS akceptujący ciąg symboli, w których przynajmniej raz wystąpiła sekwencja a,b,c

Deterministyczny automat skończony z poprzedniego podrozdziału jest szczególnym przypadkiem NAS, w którym dla każdego stanu istnieje dokładnie jedno przejście ze stanu do stanu czyli każdy DAS jest NAS.

2.3 Automat skończony z ε -ruchami

Modyfikacją niedeterministycznego automatu skończonego jest automat skończony z ε- ruchami. Model automatu w tym przypadku dopuszcza przejście ze stanu do stanu przy pustym wejściu ε. Formalnie niedeterministyczny automat skończony z ε-ruchami jest definiowany jako uporządkowana piątka:

< Q, Σ, δ, q_o, F>

gdzie:

Q, Σ, q_o, F- takie same znaczenie jak w przypadku DAS i NAS

δ- odwzorowuje Q x (Σ ∪{ε}) w 2^Q. Czyli δ jest zbiorem wszystkich stanów p takich, że istnieje przejście o etykiecie a ze stanu q do p, natomiast a jest słowem pustym ε lub symbolem ze zbioru Σ.

Dla przykładu rozpatrzmy diagram przejść AS z ε- ruchami z rysunku 16, który akceptuje ciąg symboli zawierających dowolna liczbę zer, po których następuje dowolna liczba jedynek, a następnie dowolna liczba dwójek. Oczywiście zgodnie z definicją dowolna liczba poszczególnych symboli może wynosić 0 czyli nastąpi przejście przy pustym wejściu ε:

_{0 1} ²

ε ε

start q₀ q₁ q₂

Rys.16. NAS z ε-ruchami akceptujący ciąg złożony z kilu 0, potem kilku1, a potem kilku2

Dla powyższego diagramu słowo 002 zostanie zaakceptowane gdyż istnieje droga od stanu początkowego do stanu końcowego: q₀, q₀, q₀, ε, ε, q₂, o łukach etykietowanych 0 ,0, ε, ε, 2.

Konstrukcja NAS ε- ruchami jest bardziej zrozumiała po zapoznaniu się z wyrażeniami regularnymi, które zostały omówione w następnym rozdziale.

2.4 Wyrażenia regularne

Języki akceptowane przez automaty skończone można łatwo opisać prostymi wyrażeniami zwanymi wyrażeniami regularnymi. Celem przedstawienia zapisu języków akceptowanych wprowadźmy pojęcia: złożenia i domknięcia na zbiorach łańcuchów.

Niech Σ będzie skończonym zbiorem symboli i niech L, L₁, L₂ będą zbiorami łańcuchów z Σ^*. Złożeniem L₁ i L₂, oznaczanym jako L₁ L₂, nazywamy {xy | x należy do L₁ i y należy do L₂}- oznacza to, że łańcuchy należące do L₁ L₂ tworzone są poprzez wypisanie łańcucha z L₁ , a następnie łańcucha z L₂, we wszystkich możliwych kombinacjach np. niech L₁ ={0,1}i L₂={01,101} wtedy złożenie L₁ L₂ = {001,0101, 101,1101}. Niech L⁰={ε} i Lⁱ =Ll^i-1 dla i ≥ 0. Domknięciem Kleene'ego (domknięciem) L, oznaczanym symbolem L^*, nazywamy zbiór:

∞

L^* = Lⁱ,

i = 0

a domknięciem dodatnim L, oznaczanym symbolem L⁺, zbiór

∞

L⁺ = Lⁱ,

i = 1

Tak więc L^* jest zbiorem wszystkich słów otrzymanych w wyniku złożenia dowolnej liczby słów z L, zaś L⁺ wyklucza przypadek zera słów, których złożenie określa się - ε; np. domknięciem Kleene'ego {1,0}^* ={ε, 1, 0, 11,10,01,00....} , zaś domknięciem dodatnim {1,0}⁺ = {1, 0, 11,10,01,00....}.

Wyrażenia regularne i zbiory przez nie reprezentowane definiujemy w następujący sposób:

• 
  0 jest wyrażeniem regularnym reprezentującym zbiór pusty.

• ε jest wyrażeniem regularnym reprezentującym zbiór {ε}.

• Dla każdego a z Σ, a jest wyrażeniem regularnym reprezentującym zbiór {a}.

• Jeżeli r i s są wyrażeniami regularnymi reprezentującymi odpowiednio języki R i S, to (r+s), (rs) i (r^*) są wyrażeniami regularnymi reprezentującymi odpowiednio zbiory R∪S, RS i R^*.

Dla przykładu:

• 00 jest wyrażeniem regularnym, reprezentującym {00}

• (0+1) opisuje zbiór wszystkich łańcuchów złożonych z zer i jedynek

• (0+1)^*00(0+1)^* opisuje zbiór wszystkich zer i jedynek w których przynajmniej raz wystąpiło podwojenie zer

• (1+10)^* reprezentuje zbiór wszystkich zer i jedynek rozpoczynających się od 1 i nie zawierajęcych podwojonych symboli 0.

• (0+1)^*011 opisuje wszystkie łańcuchy zer i jedynek kończące się sekwencją 011

• 0⁺ 1⁺ 2⁺ jest wyrażeniem reprezentującym dowolna liczbę zer po których następuje dowolna liczba jedynek, a następnie dowolna liczba dwójek (domknięcie dodatnie- czyli łańcuchy końcowe muszą zawierać przynajmniej po jednym reprezentancie powyższych symboli).

Udowodniono, że wyrażenia regularne reprezentują języki akceptowane przez automaty skończone co oznacza, że dla dowolnego wyrażenia regularnego istnieje odpowiadający mu NAS z ε-ruchami, co więcej wprowadzono gotowe konstruktory dla diagramów przejść pozwalające dla dowolnego wyrażenia regularnego stworzyć mechanicznie konstrukcję automatu skończonego. Wyróżniono trzy podstawowe postacie wyrażeń regularnych:

• suma teoriomnogościowa r = r₁ + r₂

• złożenie r = r₁ r₂

• domknięcie r = r₁^*

konstruktor dla sumy teoriomnogościowej r= r₁+r₂

q₁ M₁ f₁

ε ε

start q_o f_o

ε q₂ M₂ f₂ ε

Każda droga na powyższym diagramie automatu M musi rozpoczynać się od przejścia do stanu q₁ lub do stanu q₂ przy pustym wejściu ε. Jeżeli droga prowadzi do q₁, to następnie może dowolnie przebiegać w automacie M₁, aż do osiągnięcia stanu f₁, potem następuje przejście do stanu f_o, przy pustym wyjściu ε. Podobnie, jeżeli droga rozpoczęła się przejściem ze stanu q₀ do q₂ to następnie może przebiegać dowolną trasą w automacie M₂, aż do osiągnięcia stanu f₂, a następnie przejście do stanu f₀.

konstruktor dla złożenia r = r₁r₂

ε

start q₁ M₁ f₁ q₂ M₂ f₂

Każda droga z q₁ do f₂ w automacie M składa się z drogi etykietowanej jakimś łańcuchem x prowadzącej z q₁ do f₁, po której następuje przejście ze stanu f₁ do stanu q₂ przy pustym wejściu ε a następnie następuje droga z q₂ do f₂ etykietowana jakimś łańcuchem y.

konstruktor dla domknięcia r = r₁^*

ε

ε ε

start q₀ q₁ M₁ f₁ f₀

ε

Dowolna droga prowadząca z q₀ do f₂ składa się albo z drogi z q₀ do f₀ o etykiecie ε, albo też z drogi od q₀ do q₁ przy ε, po których następuje pewna liczba (w szczególnym przypadku 0) dróg z q₁ do f₁, potem znowu do q₁ przy ε, następnie znów droga z q₁ do f₁, aż w końcu droga z f₂ do f₀ przy ε.

Powyższe konstruktory są bardzo pomocne przy kreśleniu diagramów przejść NAS dla wyrażeń regularnych. Konstrukcję takiego automatu rozpoczynamy wtedy od rozłożenia wyrażenia regularnego na elementarne składowe dla których tworzymy automaty, te z kolei na podstawie konstruktorów łączymy w logiczną całość. Przeanalizujmy przykład automatu akceptującego wyrażenie regularne postaci: 01^*+1. To wyrażenie jest postaci r = r₁ + r₂ gdzie: r₁=01^*; r₂ = 1. Dla wyrażenia r₂ postać automatu jest następująca:

start q₁ ¹ q₂

wyrażenie r₁ możemy zapisać jako r₁ = r₃ + r₄ gdzie r₃= 0; r₄=1^*. Automat dla r₃ ma prostą konstrukcję, która przedstawia się następująco:

start q₃ ⁰ q₄

z kolei wyrażenie r₄ możemy zapisać jako r₄ = r^*₅ gdzie r₅ to 1, a NAS dla r₅ to:

start q₅ ¹ q₆

Wykorzystują przedstawione konstruktory zaczniemy kreślenie automatu dla wyrażenia r₄ = 1* ( konstruktor domknięcia)

ε

ε ε

start q₇ q₅ ¹ q₆ q₈ rys. a

ε

następnie dla r₁ =r₃r₄ (r= 01^*) wykorzystujemy konstruktor złożenia dokładając do rys. a następującą konstrukcję:

0 ε

start q₃ q₄ rys. a

Teraz tworzymy konstrukcję dla wyrażenia r= r₁ + r₂ (r=01^*+1) wykorzystując konstruktor sumy teoriomnogościowej.

start q₁ ¹ q₂

ε ε

q₉ q₁₀

ε ε

0 ε ε ε ε

q₃ q₄ q₇ q₅ ¹ q₆ q₈

ε

Rys.17. NAS z ε -ruchami dla wyrażenia regularnego 01^*+1.

2.5 Zastosowania automatów skończonych

Istnieje cała gama problemów z zakresu projektowania oprogramowania, które dają się uprościć poprzez automatyczną konwersję symboliki wyrażeń regularnych na efektywną implementację komputerową odpowiedniego automatu skończonego. Teorię automatów skończonych wykorzystano do:

Analizatorów leksykalnych

Tokeny (czyli bazowe kategorie syntaktyczne) języka programowania dają się niemal bez wyjątku przedstawić w postaci wyrażeń regularnych. I tak na przykład, identyfikatory ALGOLu, będące ciągami liter i cyfr rozpoczynającymi się od litery (małej czy dużej), bez ograniczenia co do długości ciągu, można wyrazić w postaci

( litera ) ( litera + cyfra )^*

gdzie litera oznacza A + B +... + Z + a + b + .. z, a cyfra - 0 + 1 + .. + 9

Identyfikatory w Fortlanie, których długość jest ograniczona do sześciu znaków i które nie mogą zawierać innych liter niż duże oraz znak $ mogą być przedstawione jako

( litera ) ( ε + litera + cyfra )⁵

Niektóre generatory analizatorów leksykalnych przyjmują jako wejście ciąg wyrażeń regularnych opisujących tokeny i wytwarzają pojedynczy automat skończony, rozpoznający dowolny token. Zazwyczaj przekształcają one wyrażenia regularne na NAS z ε-przejściami, a następnie konstruują podzbiory zbioru stanów, aby otrzymać DAS w sposób bezpośredni, zamiast wyeliminować najpierw ε-przejścia.

Edytorów tekstu

Pewne edytory tekstu oraz podobne do nich programy pozwalają na zastępowanie dowolnego łańcucha pasującego do danego wyrażenia regularnego pewnym innym łańcuchem.

Techniki

Wykorzystywane do projektowania układów przełączających na przykład działanie termostatu jest oparte na analizie temperatur i wybieraniu jednego z dwóch stanów : włączenie układu grzewczego i wyłączenie.

III. MASZYNA TURINGA

3.1 Podstawowy model maszyny Turinga

Maszyna Turinga jest prostym modelem matematycznym komputera. Opierając się na pozycji D.Harela [HARE 92] przedstawmy jej najprostszy model, natomiast pozycja J.E.Hopcrofta [HOPC 94] posłuży nam do opisu formalnego.

Podstawowy model przedstawiony na rysunku 18 ma skończone sterowanie, taśmę wejściową podzieloną na komórki (kwadraty) oraz głowicę taśmy, mogącą obserwować w dowolnej chwili tylko jedna komórkę taśmy. Taśma ma komórkę położoną najbardziej na lewo, ale jest prawowostronnie nieskończona. Każda z komórek taśmy może zawierać dokładnie jeden symbol z skończonego alfabetu symboli. Przyjmuje się umownie, że ciąg symboli wejściowych umieszczony jest na taśmie począwszy od lewej, pozostałe komórki ( na prawo od symboli wejściowych) są wypełnione specjalnym symbolem taśmowym noszącym nazwę symbolu pustego.

a₁ a₂ ... a_i ... a_n B B ...

sterowanie

skończone

Rys.18. Podstawowy model Maszyny Turinga

W zależności od obserwowanego symbolu przez głowicę taśmy oraz stanu sterowania skończonego, maszyna Turinga w pojedynczym ruchu:

• zmienia stan,

• wpisuje symbol w obserwowanej komórce taśmy, zastępując symbol tam wpisany,

• przesuwa głowicę o jedną komórkę w prawo lub w lewo.

Formalnie maszynę Turinga (MT) nazywamy:

M = <Q, Σ, Γ, δ, q₀, B, F >

gdzie:

Q- jest skończonym zbiorem stanów,

Γ - skończony zbiór dopuszczalnych symboli taśmowych,

B- symbol pusty należący do Γ,

Σ- podzbiór Γ nie zawierający B, zwany zbiorem symboli wejściowych,

δ- funkcja następnego ruchu, będąca odwzorowaniem Q x Γ w Q x Γ x { L, P }

gdzie:

L- oznacza ruch w lewo

P- ruch w prawo,

q₀- stan początkowy,

F⊆Q - zbiór stanów końcowych

Działanie maszyny Turinga przedstawia się jako diagram przejść między stanami lub jako tabelę stanów, które to pojęcia zostały omówione poniżej.

Diagram przejść jest po prostu grafem skierowanym, którego wierzchołki reprezentują stany. Krawędź prowadząca ze stanu s do stanu t nazywa się przejściem i etykietuje się ją kodem postaci (a/b, kierunek) gdzie a i b są symbolami , a kierunek określa ruch głowicy w prawo bądź w lewo. Część a etykiety jest wyzwalaczem przejścia, a część <b,kierunek> akcją:

(a / b , kierunek)

wyzwalacz akcja

W czasie swego działania maszyna Turinga, kiedy znajdzie się w stanie s i odczytywanym symbolem będzie a to nastąpi wpisanie w to miejsce b i przesunięcie o jedno pole w kierunku kierunek. Fragment przykładowego diagramu przejść przedstawia rysunek 19.

start q₁ # / #, L q₄

a / #, P

q_o # / #, L q₂

b / #, P

q₃ # / # , L

Rys.19. Fragment grafu przejść między stanami dla maszyny Turinga

Tabela stanów - która również obrazuje przejścia między stanami maszyny Turinga zawiera wszystkie symbole z skończonego alfabetu wejściowego jak również wszystkie stany w których może znaleźć się maszyna Turinga (rysunek 20). Każde pole tabeli określa:

• dla danego stanu q_i kolejny stan q_i+1

• symbol, który ma być zapisany na taśmie

• kierunek (L / P) dla ruchu głowicy

q₀ q₁ q₂ q₃

φ q₀ q₂ q₃ q₅

φ P a P c L

a q₁ q₂ q₄

b L c P a L

b q₅ q₀ q₅

φ P c L φ

c q₇ q₂

a P b L

Rys.20. Fragment tabeli stanów maszyny Turinga

Zarówno dla tabeli stanów jak i grafu przejść wyróżnia się specyficzne stany będące odpowiednio stanem początkowym i stanem (bądź stanami ) końcowym, zwane też stanami biernymi. Zakłada się , że maszyna rozpoczyna swoje działanie od swego stanu początkowego na pierwszym od lewej niepustym kwadracie taśmy i postępuje krok po kroku zgodnie z narzuconym ruchem, zaś kończy działanie po osiągnięciu stanu końcowego.

W celu zobrazowania konstrukcji tabeli stanów przeanalizujmy maszynę Turinga, która dla alfabetu wejściowego Σ ={a, b} podwaja symbole w słowie.

Przykład 8: Maszyna Turinga podwajająca symbole w słowie.

Σ ={a, b}

Γ= { φ , a , b}

Przed wypisaniem tabeli stanów przeanalizujmy jak podana maszyna Turinga ma działać. Dla słowa:

ab otrzymujemy aabb

aba otrzymujemy aabbaa

Słowo na taśmie zapisane jest jako ciąg symboli postaci na przykład φ φ φ a b φ φ φ

Na początku w kolumnie wypisujemy wszystkie symbole Γ= { φ , a , b} i stan początkowy q₀

q₀

φ q₀ jeżeli będąc w stanie q₀ odczytanym

φ, P symbolem będzie φ to pozostajemy

a nadal w tym stanie i wykonujemy

b ruch o jedno pole w prawo.

q₀

φ q₀ jeżeli będąc w stanie q₀ odczytanym symbolem będzie a

φ, P to wpisujemy w jego miejsce φ i przechodzimy w prawo

a q₁ do stanu q₁.

φ, P

Będąc w stanie q₁ musimy iść tak długo w prawo aż pominiemy wszystkie symbole łącznie z pierwszym symbolem φ. Wtedy w miejsce drugiego φ (może się ono znajdować po kilku symbolach z alfabety wejściowego) wpisujemy a i przechodzimy do stanu q₃. Jedynym słusznym symbolem napotkanym w tym stanie jest φ, w miejsce którego wpisujemy drugie a i przechodzimy do stanu q₄ (stan powrotu). Jeżeli będąc w tym stanie przejdziemy nad wszystkimi symbolami i napotkamy symbol φ, to sprawdzamy, czy są jeszcze jakieś symbole wejściowe na taśmie. Jeżeli tak to zaczynamy algorytm od początku, w przeciwnym razie przechodzimy do stanu końcowego q₁₅

q₀ q₁ q₂ q₃ q₄ q₅ q₆

φ q₀ q₂ q₃ q₄ q₅ q₁₅ q₀

φ, P φ, P a, P a, L φ, L φ, P φ, P

a q₁ q₁ q₂ q₁₅ q₄ q₆ q₆

φ, P a, P a, P a, P a, L a, L a,L

Dla symbolu b pola w tabeli stanów będą tworzone analogicznie. Ostateczny wygląd tabeli stanów przedstawia rysunek 21.

q₀ q₁ q₂ q₃ q₄ q₅ q₆ q₇ q₈ q₉ q₁₀ q₁₁ q₁₂ q₁₃

φ q₀ q₂ q₃ q₄ q₅ q₁₃ q₀ q₈ q₉ q₁₀ q₁₁ q₁₃ q₀

φ, P φ, P a, P a, L φ, L φ, P φ, P φ, P b, P b, L φ, L φ, P φ , P K

a q₁ q₁ q₂ q₁₃ q₄ q₆ q₆ q₇ q₈ q₁₃ q₁₀ q₁₂ q₁₂

φ, P a, P a, P a, P a, L a, L a, L a, P a, P a, P a, L a, L a, L K

b q₇ q₁ q₂ q₁₃ q₄ q₆ q₆ q₇ q₈ q₁₃ q₁₀ q₁₂ q₁₂

φ, P b, P b, P b, P b, L b, L b, L b , P b, P b, P b, L b, L a, L K

Rys. 21. Tabela stanów maszyny Turinga podwajająca symbole w słowie dla alfabetu wejściowego Σ ={a, b}

Przeanalizujmy kilka początkowych taktów pracy powyższej maszyny Turinga dla ciągu wejściowego: a b

Ciąg ten zapisany jest na taśmie w postaci φ φ φ a b φ φ φ φ .....

φ φ φ a b φ φ φ .... / pozostajemy w stanie q₀ i przechodzimy w prawo

φ φ φ φ b φ φ φ .. / napotkaliśmy a, wpisujemy φ i przechodzimy w prawo do stanu q₁

φ φ φ φ b φ φ φ .. / pozostajemy nadal w stanie q₁ aż dojdziemy do pierwszego znaku φ

φ φ φ φ b φ φ φ.../ po napotkaniu pierwszego φ przechodzimy w prawo do stanu q₂

φ φ φ φ b φ a φ φ.../ po napotkaniu φ wpisujemy a i przechodzimy do stanu q₃

φ φ φ φ b φ a a φ.../ w stanie q₃ wpisujemy drugie a i przechodzimy do stanu q₄, który to stan powoduje powrót na początek słowa i rozpoczęcie pracy od nowa o ile są jeszcze na taśmie symbole wejściowe

Po przeanalizowaniu wszystkich symboli wejściowych przechodzimy do stanu q₁₃, który to stan jest stanem końcowym (stan bierny ).

Dla rozpatrywanego ciągu wejściowego można określić trzy elementy w tabeli stanów:

• stan warunkowy - który powoduje przejście do określonej sekcji manipulowania danym symbolem,

• sekcja manipulowania - stany odpowiadające za przepisywanie symboli,

• powrót- stan powodujący przejście do początku i rozpoczęcie pracy od nowa

Jak zostało wcześniej wspomniane, alternatywne do tabeli stanów stosuje się graf przejść między stanami. Konstrukcję przykładowego grafu ilustruje przykład 9.

Przykład: 9

Maszyna Turinga dodającą 1 do danej liczby w zapisie dwójkowym ( inkrementacja liczby binarnej bez znaku). Analizę liczby rozpoczynamy z prawej strony.

q₀ q₁ q₂

φ q₀ q₂ K q₂

φ, L 1, L 0/1, L

0 q₂ q₂ K start q₀ φ /1 L 0 / 1, L

1, L 1, L

1 q₁ q₁ K 1/0, L

0, L 0, L q₁

1/0, L

Rys.22. Graf i tabela stanów maszyny Turinga dodającej 1 do liczby binarnej

Maszyny Turinga z przykładów: 8 i 9 rozwiązują problemy algorytmiczne związane z manipulacją danych wejściowych. Odmianę stanowią maszyny Turinga rozwiązujące problemy decyzyjne i tak pokazana w przykładzie 10 maszyna Turinga bada czy dane słowo jest palidromem.

Przykład 10:

Maszyna Turinga badająca czy dane słowo z alfabetu wejściowego Σ ={a, b, c} jest palindromem (to znaczy słowem, które czyta się tak samo z obu stron). Dodatkowo przyjmuje się, że pojedynczy symbol jest palindromem. Wprowadza się dodatkowo 2 stany akceptacji SA i nieakceptacji SN. Przejście do stanu akceptacji oznacza, że dane słowo jest palindromem, zaś przejście do stanu nieakceptacji oznacza, że słowo nie jest palindromem. Tabelę przejść miedzy stanami pokazuje rysunek 22.

q₀ q₁ q₂ q₃ q₄ q₅ q₆ q₇ q₈ q₉ q₁₀ q₁₁

φ q₀ q₂ q₁₀ q₀ q₅ q₁₀ q₀ q₈ q₁₀ q₀

φ, P φ, L φ , P φ, P φ, L φ, P φ, P φ, L φ, P φ, P SA SN

a q₁ q₁ q₃ q₃ q₄ q₁₁ q₆ q₇ q₁₁ q₉

φ, P a, P φ, L a, L a, P a, P a, L a, P a, P a, L SA SN

b q₄ q₁ q₁₁ q₃ q₄ q₆ q₆ q₇ q₁₁ q₉

φ, P b, P b, P b, L b, P φ, L b, L b , P b, P b, L SA SN

c q₇ q₁ q₁₁ q₃ q₄ q₁₁ q₆ q₇ q₉ q₉

φ, P c, P c, P c, L c, P c, P c, L c , P φ, L c, L SA SN

Rys. 22. Tabela stanów maszyny Turinga, badającej czy dane słowo jest palindromem

Różnorodność zadań stawianych przed maszyną Turinga postawiło pytanie : jakie problemy można rozwiązać za jej pomocą (oczywiście pomijając czas) ? Otóż okazuje się że : Maszyny Turinga potrafią rozwiązać każdy efektywnie rozwiązywalny problem algorytmiczny. Mówiąc inaczej, każdy problem algorytmiczny dla którego możemy znaleźć algorytm dający się zaprogramować w pewnym dowolnym języku, wykonujący się na pewnym dowolnym komputerze, nawet na takim, którego jeszcze nie zbudowano, ale można zbudować. To stwierdzenie jest jedną z wersji tzw. tezy Churcha-Turinga, którzy doszli do niej niezależnie w połowie lat trzydziestych. Istotną sprawą jest aby uświadomić sobie, że teza Churcha-Turinga jest tezą a nie twierdzeniem, zatem nie może być dowiedziona w matematycznym tego słowa znaczeniu. Jedno z pojęć, do której się odwołuje, jest bowiem nieformalnym i nieprecyzyjnym, pojęciem „efektywnej obliczalności”. Dlaczego jednak powinniśmy wierzyć tej tezie, szczególnie, jeśli nie można jej udowodnić?

Już od wczesnych lat trzydziestych badacze proponowali różne modele komputera absolutnego, wszechpotężnego, lub uniwersalnego. Chciano bowiem sprecyzować ulotne pojęcie „efektywnej obliczalności”. Na długo przedtem nim wymyślono pierwszy komputer, Turing zaproponował swoją maszynę, a Church wymyślił matematyczny formalizm funkcji zwany rachunkiem lambda (jako podstawa języka programowania Lisp). Mniej więcej w tym samym czasie Emil Post zdefiniował pewien typ systemu produkcji do manipulowania symbolami, a Stephen Kleene zdefiniował klasę obiektów zwanych funkcjami rekurencyjnymi.

Wszyscy oni próbowali użyć tych modeli do rozwiązania wielu problemów algorytmicznych, do których znane były „efektywnie wykonalne” algorytmy.

Przełomowym zdarzeniem istotnym dla wszystkich tych modeli stało się udowodnienie, iż są one równoważne w kategoriach problemów algorytmicznych, które rozwiązują. I ten fakt jest dziś nadal prawdziwy nawet dla najsilniejszych modeli, jakie można sobie wyobrazić.

Z tezy Churcha-Turinga wynika, że najpotężniejszy superkomputer z wieloma najwymyślniejszymi językami programowania, interpretatorami, kompilatorami i wszelkimi zachciankami, nie jest potężniejszy od domowego komputera z jego uproszczonym językiem programowania. Mając ograniczoną ilość czasu i pamięci mogą obydwa rozwiązać te same problemy algorytmiczne, jak również żaden z nich nie może rozwiązać problemów nierozstrzygalnych (nieobliczalnych). Schematycznie rozstrzygalność problemów przedstawia rysunek 23.

Problemy wcale nie

problemy mające algorytmów

nierozstrzygalne

teza Churcha-Turinga

problemy trudno Problemy nie mające

rozwiązywalne rozsądnych algorytmów

Problemy łatwo Problemy mające rozsądne

Rozwiązywalne algorytmy

Rys. 23. Sfera problemów algorytmicznych

IV. GRAMATYKI BEZKONTEKSTOWE

4.1 Podstawowe pojęcia gramatyk

Przez gramatykę rozumie się pewien układ reguł zadający zbiór słów utworzonych z symboli języka. Słowa te mogą być interpretowane jako obiekty językowe różnych szczebli, np. jako formy wyrazowe, grupy wyrazów i zdania. Opierając się na pracach: Z.Ałfierowej [AŁFI 77] oraz J.E.Hopcrofta [HOPC 94] spróbujemy wykazać w tym przydatność gramatyk w teorii informatyki skupiając swoje rozważania na gramatykach bezkontekstowych.

Gramatykę języka można rozpatrywać jako teorię powtarzających się prawidłowości budowy zdań zwanych syntaktyczną strukturą języka.

Syntaktyka (składnia) języka są to reguły budowy zdań w języku lub reguły budowy konstrukcji językowych. Semantyka języka jest to interpretacja tych reguł, zasady stosowania składni.

Gramatyki formalne zajmują się pojęciami abstrakcyjnymi powstającymi droga uogólnienia pojęcia formy wyrazowej, grupy wyrazów, zdania. O ile zwykłe gramatyki pozwalają określić zbiory reguł budowy zdań, o tyle gramatyki formalne stanowią pewien sposób badania i opisu zbioru reguł. rozróżnia się trzy typy gramatyk formalnych:

• rozpoznająca- jeżeli dla dowolnego rozpatrywanego słowa potrafi rozstrzygnąć, czy słowo to jest poprawne czy nie, a w przypadku odpowiedzi pozytywnej potrafi podać wskazówki dotyczące budowy tego słowa,

• generacyjna- jeżeli potrafi zbudować dowolne słowo poprawne, podając przy tym wskazówki dotyczące jego budowy oraz nie tworzy ani jednego słowa niepoprawnego,

• przetwarzająca- jeżeli dla dowolnie poprawnie zbudowanego słowa potrafi ona zbudować jego odwzorowania również w postaci słowa poprawnego, określając przy tym wskazówki dotyczące kolejności stosowania odwzorowań.

Formalnie gramatykę G określamy jako:

G= <V, T, P, S >

gdzie:

V- zbiór symboli terminalnych- skończony niepusty zbiór symboli zwany także alfabetem końcowym (zasadniczym ) gramatyki G. alfabet końcowy jest to zbiór elementów pierwotnych, z których budowane są słowa generowane przez gramatykę.

T- zbiór symboli nieterminalnych- skończony niepusty zbiór symboli zwany także alfabetem pomocniczym. Alfabet pomocniczy jest to zbiór symboli, którymi oznacza się klasy lub słowa złożone z elementów pierwotnych, czyli inaczej jest to słownik typów syntaktycznych.

P- lista produkcji- są to reguły gramatyki, czyli skończony zbiór reguł

S- głowa- symbol początkowy. Jest to wyróżniony symbol pomocniczy oznaczający klasę tych wszystkich obiektów językowych, dla których opisu przeznaczona jest gramatyka.

Podstawowym obiektem zastosowań teorii gramatyk są nie dowolne gramatyki, lecz gramatyki pewnych szczególnych typów, najważniejsze zarówno z teoretycznego jaki i praktycznego punktu widzenia. Wyróżnienia tych typów dokonuje się na podstawie postaci reguł. W teorii Chomskiego wyróżnia się cztery typy gramatyk. Gramatyki te wyodrębnia się przez nakładanie kolejno coraz silniejszych ograniczeń na układ reguł P:

• gramatyka klasy 0 - charakteryzuje się tym , że wszystkie produkcje mają postać: u→w, u∈V*\ {ε}, w ∈V*,

• gramatyka klasy 1- zwana kontekstową, nazywa się gramatykę charakteryzującą się tym, że wszystkie produkcje mają postać: uAw → ubw, u,w∈V*, A∈S , b∈V*\ {ε},

• gramatyka typu 2- zwana gramatyką bezkontekstową, która w układzie reguł P dopuszcza jedynie reguły postaci A→b, A∈S , b∈V*\ {ε},

• gramatyka klasy 3- (regularna), która w układzie reguł P dopuszcza reguły postaci A→bB (gramatyki prawostronnie regularne) albo A→Bb (gramatyki lewostronnie regularne), A∈S, B∈S∪ {ε}, b∈T*\ {ε}.

Można się łatwo przekonać, że każda gramatyka klasy i jest jednocześnie gramatyką klasy j, dla 0 ≤ j ≤ i. Wynika to stąd, że każdy zbiór ciągów wywodliwych zgodnie z gramatyką klasy i jest jednocześnie zbiorem ciągów wywodliwych zgodnie z gramatyką niższych klas. Odwrotne stwierdzenie nie jest jednak prawdziwe. Można bowiem podać przykłady zbiorów ciągów wywodliwych zgodnie z gramatyką i, dla których nie sposób skonstruować gramatyki wyższej klasy. Ogólnie powiedziawszy, im wyższa klasa gramatyki, tym mniej precyzyjnie określa się rozmaitość wywodliwych ciągów.

Jako ilustrację do poszczególnych gramatyk rozpatrzmy klasyczny przykład ciągów: aa.......bb........cc......, które w skrócie będziemy zapisywać: a^kb^lc^m.

k razy l razy m razy

Jeśli nie nakładamy żadnych ograniczeń na wartości k, l, m, to bez trudu możemy znaleźć prawostronnie regularną gramatykę:

G₃= (V₃, T₃, P₃, S)

gdzie

V₃={a,b,c}, T₃={S,V,U}, zaś lista produkcji

P₃={ S→aS,

S→aV,

V→bV,

V→bU,

U→cU,

U→c}

Jeśli jednak chcemy otrzymać nieco bardziej ograniczone ciągi, w których k=m to nie można już dla nich zbudować gramatyki regularnej, natomiast można je określić przez gramatykę bezkontekstową

G₂= (V₂, T₂, P₂, S)

gdzie

V₂={a,b,c}, T₂={S,V}, zaś lista produkcji

P₂= { S→aSc,

S→aVc,

V→Vb,

V→b }

Zdefiniowanie ciągów o jednakowej liczbie wystąpień każdej z liter (k=l=m) wymaga już użycia gramatyki kontekstowej lub gramatyki klasy 0, na przykład

G₁= (V₁, T₁, P₁, S)

gdzie

V₁={a,b,c}, T₁={S,U}, zaś lista produkcji

P₁={ S→abc,

S→aSUc,

cU→Uc,

bU→bb}

4.2 Gramatyki bezkontekstowe

Gramatyki bezkontekstowe, podobnie jak omawiane wcześniej zbiory regularne mają szerokie zastosowanie praktyczne. Są one wykorzystywane do definiowania języków programowania, do formalizacji pojęcia analizy syntaktycznej, do upraszczania translacji języków programowania.

Gramatyka bezkontekstowa to skończony zbiór zmiennych (zwanych też symbolami niekońcowymi, symbolami pomocniczymi lub kategoriami syntaktycznymi), z których każda reprezentuje pewien język. Języki reprezentowane przez zmienne opisywane za pomocą wzajemnej rekursji, z zastosowaniem pewnych symboli pierwotnych, zwanych symbolami końcowymi. Reguły wiążące ze sobą zmienne zwane są produkcjami.

Pierwotną motywacją wprowadzenia pojęcia gramatyk bezkontekstowych był opis języków naturalnych. W ich kontekście możemy pisać reguły:

<zdanie> <fraza rzeczownikowa> <fraza czasownikowa>

<fraza rzeczownikowa> <przymiotnik > <fraza rzeczownikowa>

<fraza rzeczownikowa> <rzeczownik>

<rzeczownik> chłopiec

<przymiotnik> mały,

gdzie kategorie syntaktyczne są ujęte w nawiasy kątowe, a symbole końcowe są reprezentowane za pomocą słów nie ujętych w nawiasy np.: „chłopiec”

Rozważania ligwistów posłużyły w informatyce do opisu języków programowania za pomocą notacji zwanej notacją Backusa-Naura (NBN), będącej notacją gramatyki bezkontekstowej z pewnymi drobnymi zmianami dotyczącymi formatu oraz kilkoma skrótami notacyjnymi. Takie użycie gramatyk bezkontekstowych bardzo uprościło definicje języków programowania oraz konstrukcję kompilatorów. Dla przykładu weźmy następujący zbiór produkcji:

1. <wyrażenie> <wyrażenie> + <wyrażenie>

2. <wyrażenie> <wyrażenie> * <wyrażenie>

3. <wyrażenie> (<wyrażenie>)

4. <wyrażenie> id

który definiuje wyrażenie arytmetyczne z operatorami + i * oraz argumentami reprezentowanymi przez symbol id. Pierwsze dwie produkcje mówią, że wyrażenie może być złożone z dwóch wyrażeń połączonych znakiem dodawania lub mnożenia. trzecia produkcja mówi, że wyrażenie może być innym wyrażeniem ujętym w nawiasy. Ostatnia zaś mówi, że pojedynczy argument jest wyrażeniem.

Stosując te produkcje wielokrotnie, możemy otrzymać coraz bardziej złożone wyrażenia. Dla przykładu:

<wyrażenie> ⇒ <wyrażenie> * <wyrażenie>

⇒ ( <wyrażenie>) * <wyrażenie>

⇒ <wyrażenie> * id

⇒ ( <wyrażenie> + <wyrażenie> ) *id

⇒ <wyrażenie> + id) * id

⇒ (id +id) * id

Symbol ⇒ oznacza tu akt wyprowadzenia, to jest zastępowania zmiennej prawą stroną produkcji dla tej zmiennej.

Formalnie gramatykę bezkontekstową definiujemy jako:

G=<V, T, P,S>

gdzie:

V i T- odpowiednio skończone zbiory zmiennych i symboli końcowych,

P - jest skończonym zbiorem produkcji (każda produkcja ma postać A->α, gdzie A jest zmienną, a α jest łańcuchem symboli z (V∪T)* ),

S- jest specjalną zmienną, zwaną symbolem początkowych.

Dla zdefiniowania języka generowanego przez gramatykę G=<V, T, P, S> wprowadźmy notację do reprezentowania wyprowadzeń. Najpierw definiujemy dwie relacje: ⇒ i ⇒

pomiędzy łańcuchami z (V∪T)*. Jeśli A β jest produkcją z P, a α i γ są dowolnymi łańcuchami z (V∪T)*, to αAγ ⇒ αβγ.

Mówimy, że produkcja A β zastosowana do łańcucha αAγ daje w wyniku αβγ, lub że αβγ jest bezpośrednio wyprowadzalny z αAγ w gramatyce G. Dwa łańcuchy są związane relacja ⇒ dokładnie wtedy, gdy drugi z nich można otrzymać, z pierwszego poprzez zastosowanie jakiejś produkcji.

Przypuśćmy, że α₁ ,α₂, .....α_m są łańcuchami z (V∪T)*, , m ≥ 1, oraz

α₁⇒ α₂, α₂ ⇒ α₃, .....α_m-1⇒α_m

wtedy piszemy:

α₁ ⇒ α_m

i mówimy, że α_m jest wyprowadzalny z α₁ w gramatyce G.

Język generowany przez gramatykę G to L(G) = {w|w należy do T* i S ⇒ w}.

A zatem łańcuch w należy do L(G), jeśli spełnione są dwa następujące warunki:

1. w składa się wyłącznie z symboli końcowych.

2. w jest wyprowadzalny z S.

Język L nazywamy językiem bezkontekstowych (JBK), jeśli jest on tożsamy z L(G) dla pewnej gramatyki G. Łańcuch α złożony z symboli końcowych i zmiennych nazywamy formą zdaniową jeśli S⇒α. mówimy, że gramatyki G₁ i G₂ są równoważne, jeżeli: L(G₁) = (G₂)

Przykład 11:

Mamy gramatykę G=<V,T,P,S>, gdzie V={S}, T={a,b}, i P={S aSb, S ab}. Jedyną zmienną jest tu S, a i b są symbolami końcowymi. Istnieją dwie produkcje S aSb, S ab. Stosując pierwszą z nich n-1 razy, a następnie jeden raz drugą otrzymujemy:

S⇒ aSb ⇒ aaSbb ⇒ a³Sb³ ⇒...⇒ a^n-1Sb^n-1 ⇒ aⁿbⁿ

4.3 Drzewa wyprowadzenia

Użyteczne jest przedstawienie wyprowadzeń w postaci drzew (znacznik struktury frazowej). Wierzchołki drzewa wyprowadzenia (lub rozkładu) są etykietowane symbolami końcowymi lub zmiennymi gramatyki, ewentualnie symbolem ε. Jeśli wierzchołek wewnętrzny n jest opatrzony etykietą A, a synowie n są opatrzeni etykietami X₁,X₂...,X_k w kolejności od lewej do prawej, to A X₁X₂...X_k musi być produkcją rozpatrywanej gramatyki. Rysunek 24 pokazuje drzewo wyprowadzenia dla przytoczonych wcześniej reguł:

1. <wyrażenie> <wyrażenie> + <wyrażenie>

2. <wyrażenie> <wyrażenie> * <wyrażenie>

3. <wyrażenie> (<wyrażenie>)

4. <wyrażenie> id

< wyrażenie>

< wyrażenie> * < wyrażenie>

( < wyrażenie> ) id

< wyrażenie> + < wyrażenie>

id id

Rys.24. Drzewo wyprowadzenia

Bardziej formalnie, niech G= (V,T,P,S ) będzie gramatyką bezkontekstową. Drzewo D jest drzewem wyprowadzenia (lub rozkładu) dla G, jeśli:

• każdy wierzchołek drzewa D ma etykietę, będącą symbolem z V ∪ T∪ {ε},

• etykietą wierzchołka drzewa D jest S,

• jeśli wierzchołek wewnętrzny drzewa S jest opatrzony etykietą A, to A musi należeć do V,

• 
  jeżeli wierzchołek n drzewa D ma etykietę A, a wierzchołki n₁,n₂.....n_k są synami wierzchołka n uszeregowanymi od lewej do prawej i opatrzonymi odpowiednio etykietami X₁,X₂......,X_k to A X₁X₂......X_k musi być produkcją z P,

• jeżeli wierzchołek n drzewa D ma etykietę ε, to n jest liściem drzewa D oraz jedynym synem swego ojca.

Przykład 12:

Rozpatrzmy gramatykę G=({S,A},{a,b}, {P,S}), gdzie P składa się z następujących produkcji:

S aAS | a

A SbA | SS | ba

Wywód dla tej gramatyki S ⇒ aAS ⇒ aSbAS ⇒ aabAS ⇒ aabbaS ⇒ aabbaa, zaś drzewo wyprowadzenia pokazane zostało na rysunku 25.

S

a A S

S b A a

a b a

Rys.25. Drzewo wyprowadzenia dla przykładu 12

Dwa znaczniki struktury frazowej (drzewa wyprowadzeń) są uważane za tożsamościowo równe, jeżeli posiadają one jednakową strukturę gałęzi i jednakowe etykiety przy odpowiednich węzłach.

Ponieważ liczba reguł jest skończona, natomiast liczba znaczników może być nieskończona, to mogą istnieć takie symbole alfabetu pomocniczego, które powtarzają się w znacznikach struktury dowolną ilość razy. Co więcej, mogą istnieć takie łańcuchy drzewa, które zawierają pewien symbol więcej niż n razy dla dowolnego z góry ustalonego n.

Element syntaktyczny nazywa się elementem rekursywnym, jeżeli dla pewnego z góry ustalonego n istnieje takie drzewo struktury, którego łańcuch zawiera ten symbol jako nazwę węzła więcej niż n razy. Wyodrębnia się trzy rodzaje elementów rekursywnych:

• element A nazywa się leworekursywnym, jeżeli podporządkowane jemu drzewo zawiera A tylko w łańcuchu wysuniętym najbardziej w lewo,

• element A nazywa się praworekursywnym, jeżeli podporządkowane mu drzewo zawiera A tylko w łańcuchu wysuniętym najbardziej w prawo,

• element A nazywa się samozanurzającym, jeżeli podporządkowane mu drzewo zawiera A w pewnym łańcuchu wewnętrznym.

a) A b) A c) A

B C B C B C

A A A

Rys.26. elementy rekursywne: a) leworekursywny, b) samozanurzający

c) praworekursywny

Teoria gramatyk formalnych, stanowi bardzo rozległą dziedzinę wiedzy, toteż w niniejszym rozdziale została przedstawiona gramatyka bezkontekstowa mająca najszersze zastosowanie w informatyce.

V. OPIS PROGRAMÓW

Rozdział V jest opisem programów ilustrujących zagadnienia omówione w części teoretycznej. Zostały one napisane przy użyciu języka programowania C++ w wersji 4.0 z wykorzystaniem biblioteki OWL. Jedynym wymogiem dla uruchomienia programów jest środowisko graficzne WINDOWS (począwszy od wersji 3.0). Wersje źródłowe programów są dołączone do niniejszej pracy i mogą być w pełni wykorzystywane przez osoby kontynuujące pracę: „Pakiet programów edukacyjnych z zakresy przedmiotu wprowadzenie do informatyki”.

5.1. ONP

Program ONP jest ilustracją graficzną do rozdziału pierwszego: „Zasady automatycznej translacji”. Menu programu zostało podzielone na trzy części:

• Zadania- opcja pozwala na wybranie jednego z pięciu zadań do procesu translacji bez możliwości definiowana własnych zadań,

• Praktyka- opcja pozwalająca wpisanie własnych zadań do procesu translacji,

• Teoria-opcja pozwalająca na zapoznanie się z podstawowymi wiadomościami teoretycznymi,

Menu główne programu ONP

Po wybraniu opcji zadania, mamy możliwość wybrania jednego z pięciu przykładowych zadań obrazujących proces translacji. Dodatkowo wybieramy stopień translacji:

• Do ONP- przedstawia proces translacji wyrażeń arytmetycznych do postaci ONP,

• 
  ONP język symboliczny - przedstawia proces translacji z ONP na język symboliczny.

Po wybraniu opcji do ONP ukaże się nam następujące okienko dialogowe:

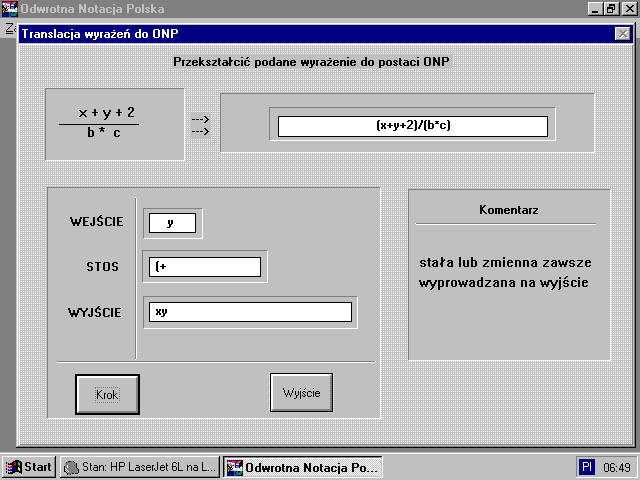
Przycisk KROK pozwala śledzić poszczególne takty translacji, natomiast przycisk WYJŚCIE kończy analizę danego zadania. W polu komentarz na bieżąco jest komentowany każdy krok procesu translacji, a pola WEJŚCIE, STOS, WYJŚCIE odzwierciedlają aktualny stan rozpatrywanego zadania. Zadania zostały tak dobrane aby użytkownik miał możliwość poznać wszystkie aspekty procesu translacji wyrażeń do postaci ONP.

Po wybraniu opcji ONP j.symboliczny ukaże się nam następujące okienko dialogowe:

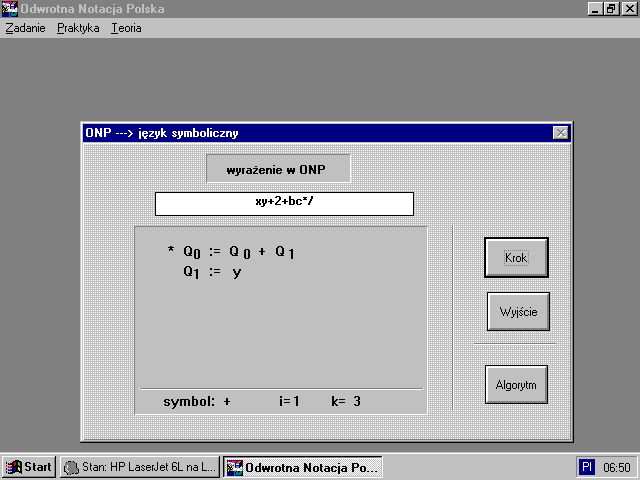
Przyciski KROK i WYJŚCIE mają takie samo znaczenie jak poprzednio, natomiast przycisk ALGORYTM wyświetla algorytm translacji na drodze ONP język symboliczny. Program został tak skonstruowany, że jeżeli wybrano zadanie n do procesu translacji to automatycznie jest wypisywane w okienku wyrażenie w ONP odpowiednio przekształcone wyrażenie arytmetyczne z pierwszej fazy translacji.

Opcja teoria uruchamia plik pomocy do WINDOWS wdihelp.hlp, który jest wspólny dla wszystkich programów. Przykładowe okienko dla ONP pokazane zostało poniżej:

5.2. AS

Program AS jest programem edukacyjnym do rozdziału drugiego : „Automat skończony”. Menu programu zostało podzielone na trzy części:

• Wyrażenia regularne- opcja pozwala na wybranie zadań związanych z wyrażeniami regularnymi.

• Automaty- opcja pozwalająca na wybranie zadań związanych z automatami skończonymi,

• Teoria-opcja pozwalająca na zapoznanie się z podstawowymi wiadomościami teoretycznymi,

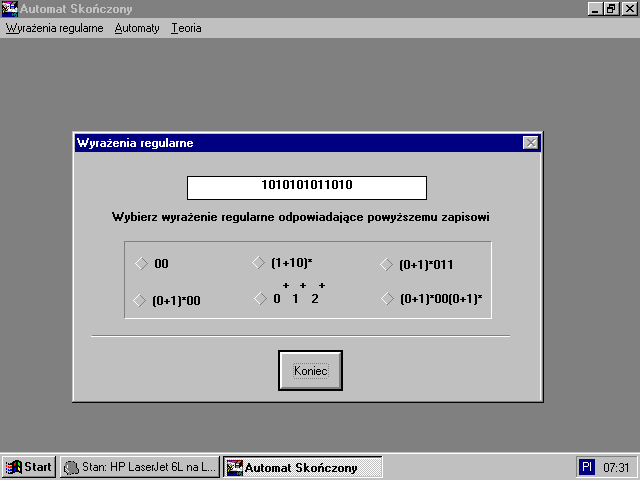
Po wybraniu opcji wyrażenia regularne ukaże się następujące okienko dialogowe:

Pierwsze trzy zadania są oparte na tej samej zasadzie to znaczy dla podanego ciągu wejściowego należy wskazać odpowiadające temu ciągowi wyrażenie regularne.

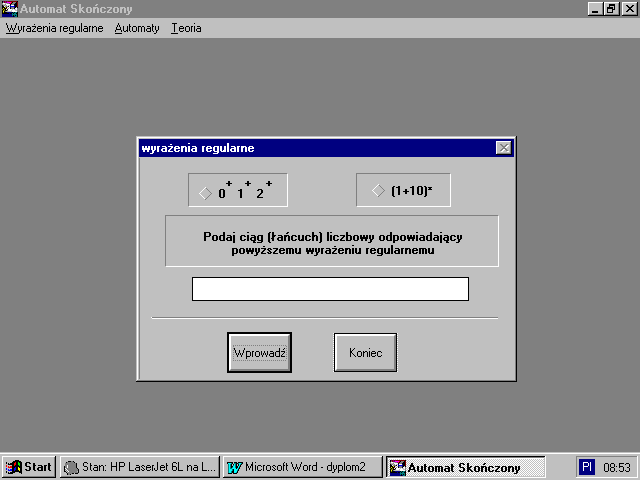
Dwa następne zadania polegają na wpisaniu odpowiedniego ciągu znakowego dla wybranego wyrażenia regularnego co przedstawia poniższy rysunek :

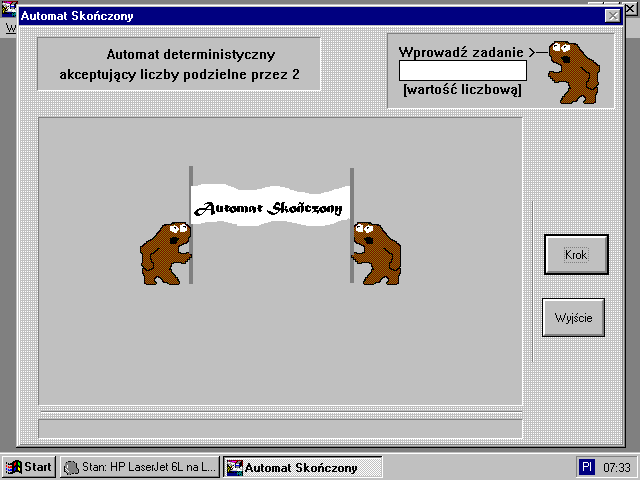
Po wybraniu opcji automaty użytkownik spotka się z przykładowym okienkiem dialogowym w którym należy podać odpowiedni ciąg celem zobrazowania dalszej pracy automatu skończonego.

Przycisk KROK powoduje wczytanie podanego ciągu, a zarazem krokowo przedstawia przejścia automatu skończonego pomiędzy stanami. Dodatkowo po każdym wczytaniu ciągu jest sprawdzana poprawność zadania to znaczy, że w przypadku analizy cyfr nie mogą zostać wpisane inne znaki i użytkownik może spotkać się z komunikatem o błędnym wprowadzeniu zadania. Przycisk WYJŚCIE podobnie jak to ma miejsce we wszystkich innych programach powoduje opuszczenie analizy przejść automatu skończonego.

Po wczytaniu zadania w kolejnym okienku dialogowym zostanie wyrysowany konkretny automat skończony.

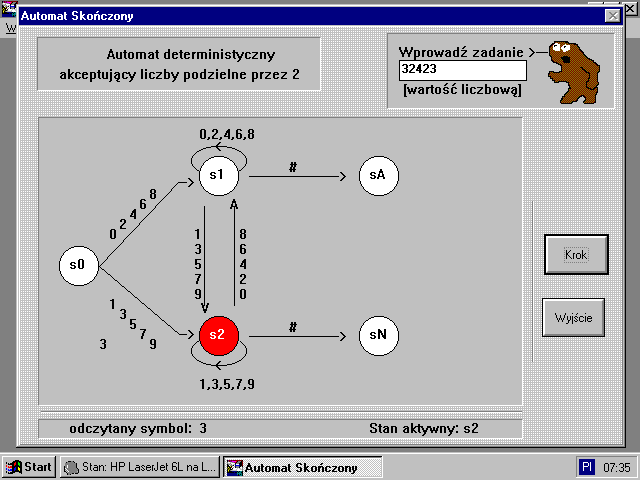
Aktywny stan w jakim się znajduje automat skończony jest zaznaczany kolorem czerwonym, zaś stany nieaktywne kolorem białym. Dodatkowo u dołu ekranu jest wypisywany aktualnie analizowany symbol i aktywny w danej chwili stan automatu.

5.3. MT

Program MT jest programem edukacyjnym do rozdziału trzeciego : „Maszyna Turinga”. Menu programu zostało podzielone na dwie części:

• Zadania- opcja pozwala na wybranie jednego z pięciu zadań związanych z maszyną Turinga,

• Teoria-opcja pozwalająca na zapoznanie się z podstawowymi wiadomościami teoretycznymi,

Po wybraniu opcji zadania i wyborze konkretnego zadania użytkownik powinien wpisać odpowiedni ciąg do dalszej analizy zadania.

Przycisk KROK pozwala na krokową analizę działania wybranej maszyny Turinga, zaś przycisk AUTOMAT w odstępach sekundowych symuluje pracę maszyny Turinga. Analogicznie jak w pozostałych programach przycisk WYJŚĆIE kończy pracę z wybraną maszyną Turinga.

Po wybraniu konkretnego zadania i wpisaniu słowa początkowego użytkownik może spotkać się z jednym z następujących okien dialogowych:

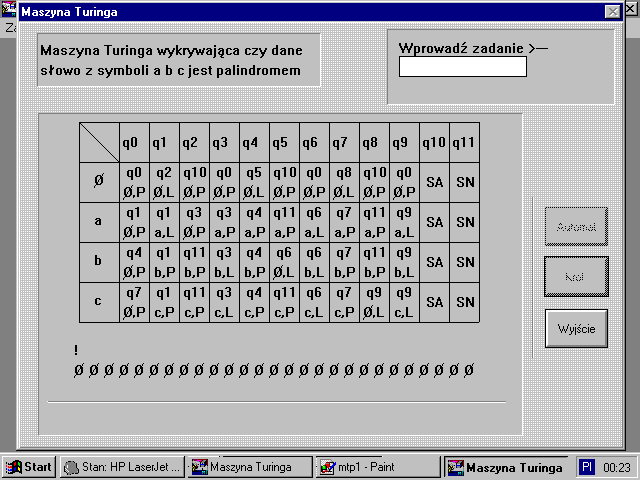
Konstrukcja tego okienka w części pierwszej pokazuje tabelę przejść między stanami, zaś u dołu okienka symulowana jest taśma, z umieszczonymi na niej symbolami. Analizowany symbol na taśmie jest oznaczony znakiem ” ! ” , a w niektórych zadaniach aktywne stany dodatkowo wyróżnione są innym kolorem.

Przykładowe okienka z zadaniami w programie MT

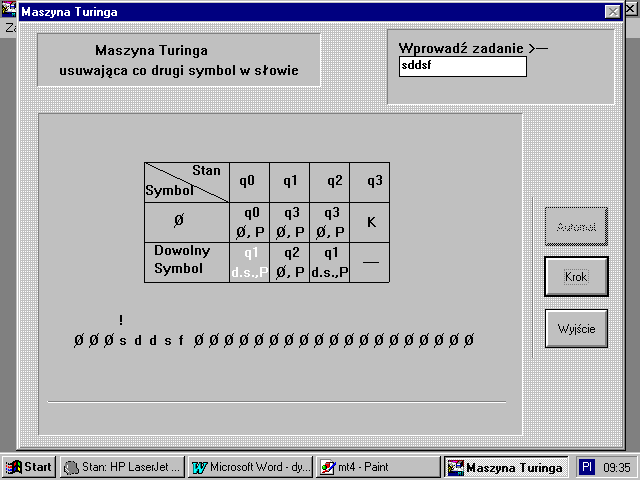
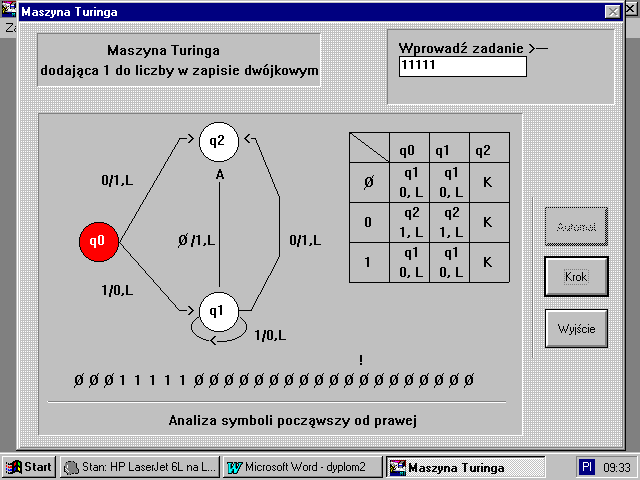
5.4. GR

Program GR jest programem edukacyjnym do rozdziału czwartego : „Gramatyki bezkontekstowe”. Menu programu zostało podzielone na dwie części:

• Test- opcja pozwala na wybranie okienka dialogowego obsługującego test z zakresu gramatyk formalnych,

• Teoria-opcja pozwalająca na zapoznanie się z podstawowymi wiadomościami teoretycznymi,

Przykładowe ekrany pytań testowych są przedstawione poniżej

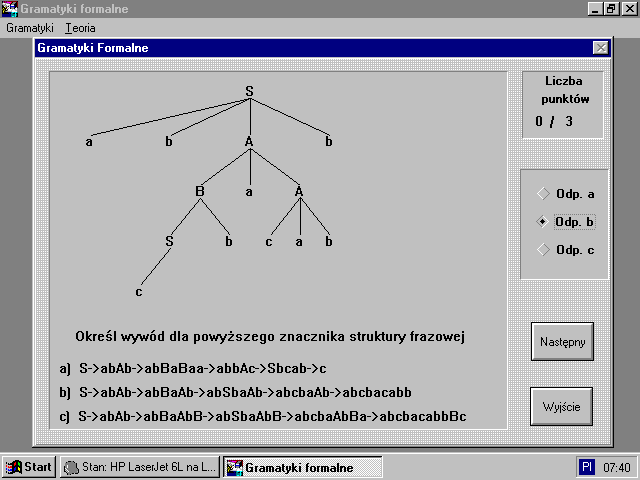
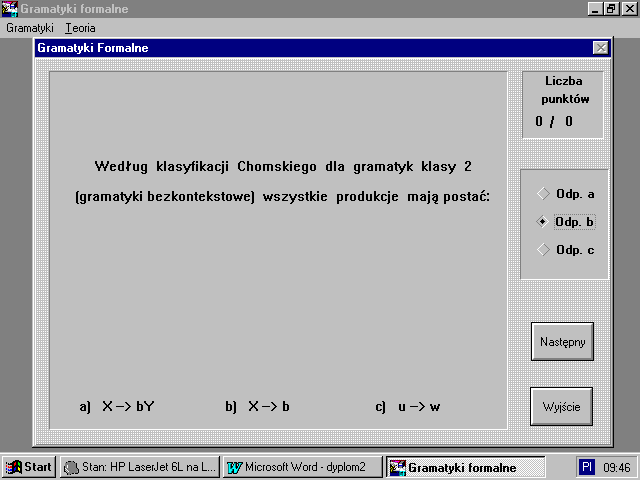
5.5. Zawartość dysku CD-ROM

Płyta kompaktowa dołączona do pracy posiada następującą strukturę:

..

PROGRAMY

onp.exe

as.exe programy omówione w rozdziale 5

mt.exe

gr.exe

wdihelp.hlp

ZRODLA

ONP

AS pliki źródłowe *.cpp, *.rc, *.h,

MT

GR

HLP

DOC

dyplom.doc dokumentacja bez opisu programów - skrypt

dyplom2.doc pełny tekst pracy magisterskiej

Na dyskietce dołączonej do pracy znajdują się cztery programy : onp.exe, as.exe, mt.exe, gr.exe oraz plik pomocy dla Widows wdihelp.hlp.

LITERATURA

1. [AŁFI 77] Zoja Ałfierowa: Teoria algorytmów. PWN, Warszawa, 1977.

2. [BANA 96] L. Banachowski, K.Diks, W.Rytter: Algorytmy i struktury danych. WNT, Warszawa, 1996.

3. [GNIŁ 89] Marian Gniłka, Juliusz Haschka: Istota informatyki. IWZZ, Warszawa 1989.

4. [HARE 92] Dawid Harel: Rzecz o istocie informatyki. WNT, Warszawa, 1992.

5. [HOPC 94] John E. Hopcroft, Jefrey D. Ullman :Wprowadzenie do teorii automatów, języków i obliczeń. PWN, Warszawa, 1994.

6. [KOZI 94] Stanisław Kozielski: Zbiór zadań z podstaw informatyki. Politechnika Śląska-Skrypt uczelniany nr 1842, Gliwice, 1994

7. [MAJC 94] Adam K. Majczak: Praktyczne programowanie w C++. INTERSOFTLAND, Warszawa, 1994.

8. [TURS 77] Władysław M.Turski: Propedeutyka informatyki. PWN, Warszawa, 1977.

9. [WRÓB 97] Piotr Wróblewski: Programowanie w Windows dla praktyków. Helion, Gliwice, 1997 .

10.[ZALE 95] Andrzej Zalewski: Programowanie w językach C i C++ z wykorzystaniem pakietu Borland C++. Nakom, Poznań 1995.

65

---